曲柄连杆机构受力分析概要

发动机曲柄连杆机构组成作用和受力分析发动机的曲柄连杆机构是发动机最重要的机构，它的重要性体现在在三点：缸体和缸盖组成发动机工作的基础部件；实现活塞的往复直线运动和曲轴旋转动行的转变；保证气缸的密封，这是发动机正常工作的重要保证！发动机曲柄连杆机构的机体组是发动机工作的基础很多人将曲柄连杆机构的组成分为三部分：机体组、活塞连杆组和曲轴飞轮组。

机体组包括缸体、缸盖、缸垫、缸套和油底壳等，它们是发动机工作的基础部件，如在缸体和缸盖内设有润滑油道和冷却水道，并在缸体上安装有润滑系统的机油泵，机油滤清器和冷却系统的循环水泵。

发动机配气机构基本全部在缸盖安装。

活塞连杆组包括活塞、连杆、活塞环、活塞销、连杆等。

曲轴飞轮组包括曲轴、连杆轴承、主轴承、止推垫、飞轮等。

活塞连杆组和曲轴飞轮组实现活塞的往复直线运动和曲轴旋转动行的转变：在做功冲程中，活塞带动曲轴做旋转运动，对外输出动力。

而在进气、压缩、排气行程中又把曲轴的旋转运动转变成活塞的往复直线运动，为做功冲程做好准备。

曲柄连杆机构的活塞连杆组和曲轴飞轮组曲柄连杆机构一个非常重要的作用是保证气缸的密封性能，建立足够的气缸压力，它是发动机正常工作的保证。

气缸的密封需要缸套、活塞和活塞环的良好配合实现。

良好的配合间隙保证了气缸内的高压燃汽不会窜入油底壳，油底壳的机油不会窜入气缸参与燃烧。

曲柄连杆机构的活塞，活塞环和缸套磨损后，配合间隙增大，气缸的密封性能下降，气缸内的燃汽窜入油底壳，加速机构的变质，发动机动力下降。

同时油底壳机油进入气缸参与燃烧，发动机冒蓝烟，加速机油的消耗和发动机内部积碳的生成。

曲柄连杆机构主要承受气体作用力、往复惯性力、旋转离心力及机件摩擦力的作用。

并且高温、高速、高压、存在腐蚀和润滑困难。

发动机工作时，曲柄连杆机构直接与高温高压气体接触，曲轴的旋转速度又很高，活塞往复运动的线速度相当大，同时与可燃混合气和燃烧废气接触，曲柄连杆机构还受到化学腐蚀作用，并且润滑困难。

汽车设计课程设计说明书题目：曲柄连杆机构受力分析一、课程设计要求根据转速、缸内压力、曲柄连杆机构结构参数，计算发动机运转过程中曲柄连杆机构受力，完成计算报告，绘制曲柄连杆机构零件图。

1.1 计算要求掌握连杆往复惯性质量与旋转离心质量折算方法；掌握曲轴旋转离心质量折算方法；掌握活塞运动速度一阶、二阶分量计算方法；分析活塞侧向受力与往复惯性力及相应设计方案；分析连杆力及相应设计方案；采用C语言编写曲柄连杆机构受力分析计算程序；完成曲柄连杆机构受力计算说明书。

1.2 画图要求活塞侧向力随曲轴转角变化连杆对曲轴推力随曲轴转角变化连杆轴承受力随曲轴转角变化主轴承受力随曲轴转角变化活塞、连杆、曲轴零件图（任选其中两个）二、计算参数2.1 曲轴转角及缸内压力参数曲轴转速为7000 r/min，缸内压力曲线如图1所示。

图1 缸内压力曲线2.2发动机参数本计算过程中，对400汽油机进行运动和受力计算分析，发动机结构及运动参数如表1所示。

表1 发动机主要参数参数指标发动机类型汽油机缸数 1缸径D mm 91冲程S mm 63曲柄半径r mm 31.5连杆长l mm 117偏心距e mm 0排量 mL 400活塞组质量'm kg 0.425连杆质量''m kg 0.46m kg 0.231曲轴旋转离心质量k标定功率及相应转速 kw/（r/min）17/7500最高爆发压力 MPa 5～6MPa三、计算内容和分析图3.1 运动分析3.1.1曲轴运动近似认为曲轴作匀速转动，其转角，t t t n 37006070002602πππα=⋅==s rad s rad dt d /04.733/3700≈==παω3.1.2活塞运动规律图2 中心曲轴连杆机构简图1）活塞位移 111cos cos x r αβλλ⎡⎤⎛⎫⎛⎫=+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，其中()()⎥⎦⎤⎢⎣⎡-+-⋅=⎥⎦⎤⎢⎣⎡-+-≈⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛+≈-=-≈-=-==⋅=≈==t t r r x l r l r 04.733cos 14685.3104.733cos 15.31)2cos 1(4)cos 1(sin 2111cos 11)2cos 1(21sin sin 211)sin 1(sin 1cos sin sin /sin 27.01175.31/2222221222αλααλλαλαααλαλββαλαβλ又活塞位移曲线如图3所示图3 活塞位移曲线2）活塞速度 ⎪⎭⎫ ⎝⎛+==αλαω2sin 2sin r dt dx v()αλαωα2cos cos +=r d dv令0=αd dv， 有()01cos 2cos 2cos cos 2=-+=+αλααλα，︒≈⎥⎥⎦⎤⎢⎢⎣⎡-+⎪⎭⎫ ⎝⎛==-+84.6412141arccos 021cos 21cos 2max2λλααλα曲轴转角解得最大活塞速度时的即最大活塞速度 ⎪⎭⎫⎝⎛+=max max max 2sin 2sin αλαωr vsm s rad mm /86.2326.169sin 11725.3163.84sin /37005.31≈⎪⎭⎫⎝⎛︒⨯+︒⋅⨯=π平均活塞速度 s m r mm n r Sn v m /7.1430min/70005.31230230=⋅⋅=⋅==活塞速度曲线如图4所示图4 活塞速度曲线3）活塞加速度 ()αλαωαα2cos cos 2+=⋅==r dtd d dv dt dv j()αλαωα2sin 2sin 2+-=r d dj令0=αd dj，有 ()0cos 41sin cos sin 4sin 2sin 2sin =+=+=+αλαααλααλα，由0sin =α，即︒=0α或︒=180α时，得正、负最大加速度：），得第二＞时（仅当，得当由418.175)41arccos(0cos 41/3.12356)1(,/6.21496)1(22180220λλααλλωλωαα ≈-='=+-≈--=≈+===s m r j s m r j 个负最大加速度，即()αλαωα'+'='2cos cos 2r j()[]2222/4.12418811cos 2cos sm r r -≈⎪⎭⎫ ⎝⎛+-=-'+'=λλωαλαω 活塞加速度曲线如图5所示图5 活塞加速度曲线3.1.3连杆运动规律 1）连杆摆动角由αλβsin sin =，得()αλβsin arcsin =()λβλβ-==arcsin arcsin min max2）连杆摆动角速度 dtd βω=1 αλαλωβαλωβωαλωββαλβ221sin 1cos cos cos cos cos sin sin -===⇒=⋅⇒=dt d dt d 3）连杆摆动角加速度 ⎪⎪⎭⎫⎝⎛-==αλαλωωε2211sin 1cos dt d dt d ()()232222sin 1sin 1αλαλλω---=3.2 受力分析 3.2.1 活塞气体力活塞气体力 ()h g g F p p P ⋅-=010 N其中：g p 缸内气体压力 bar (1bar=5101⨯pa)；0p 大气压力 一般取0p =1bar ；04.65104911042222≈⨯⋅=⨯=--ππD F h cm 2活塞气体力曲线如图6所示图6 活塞气体力曲线3.2.2 往复惯性力往复运动质量 '''3.0m m m j ⋅+=，连杆质量—活塞组质量，—m m ''' 563.046.03.0425.0=⨯+= kg 往复惯性力 ()2cos cos2j j P m r ωαλα=-⋅⋅+⋅ 往复惯性力曲线如图7所示图7 往复惯性力曲线3.2.3 活塞侧压力及连杆力气体压力与往复惯性力作用在气缸中心线上，将往复惯性力用单位活塞面积的力计量，则合成的单位活塞面积的力为：()αλαω2cos cos 2+-=+=hj g j g F r m p p p pk t p p l n 、、、对曲轴连杆机构的作用如右图所示。

第三章曲柄机构受力分析3.1曲柄连杆机构运动学曲柄连杆机构的任务是将活塞的往复运动转化为曲柄的旋转运动，在往复活塞式汽车发动机中基本上采用两种曲柄连杆机构；中心曲柄连杆机构；偏心曲柄连杆机构。

（l）、中心曲柄连杆机构：其气缸轴线通过曲轴轴线。

这种机构的运动特性完确定，其中r为曲柄半径，L为连杆长度（连杆大小头孔中心间距全由连杆比λ=rι离）（2）、偏心曲柄连杆机构：其气缸轴线偏离曲柄轴线。

这种机构的特性参数除连杆比λ，还有偏心率ξ=℮，其中ℯ为气缸轴线相对曲轴轴γ线的偏移量。

下面讨论应用最广泛的中心曲柄连杆结构的运动学。

3.1.1中心曲柄连杆机构运动学中心曲柄连杆机构在汽车发动机中应用最广泛。

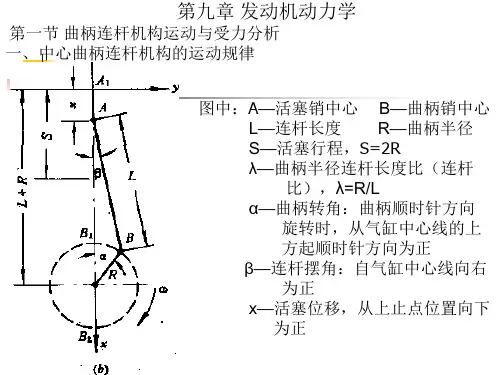
机构简图如图3一1所示。

它在运动时，活塞A作往复直线运动，曲柄OB作旋转运动，连杆AB作平面复合运动。

研究曲柄连杆机构图运动学的重点是研究活塞的运动规律，因为曲柄的运动状态比较简单，连杆的运动虽然较复杂，但可把它看成一部分随活塞A运动，另一部分随连杆轴径B运动，其运动所引起的其他后果对我们所研究的问题影响较小。

图3一2中，O点表示曲轴中心，A点表示活塞销中心位置、也就是活塞的位置，OB表示曲柄半径:，AB表示连杆长度l。

曲柄转角α是从气缸轴线顺着曲柄转动方向度量。

当α二0º时，对应的Aˊ和Βˊ表示活塞和连杆轴径在上止点位置；当α﹦180º时，对应的Aˊ和Βˊ表示活塞和连杆轴径在下止点位置。

β为连杆轴线偏离气缸轴线的角度，称为连杆摆动角，逆时针为正、顺时针为负。

下面分别研究曲柄、活塞和连杆的运动规律：1、曲柄运动通常近似地认为汽车发动机中曲柄是作匀谏转动，其转角α=360π60t=6nt度。

式中t表示时间，n表示汽车发动机转速（转/分）。

角速度ω=dαdt =πn30弧度/秒≈常数。

因为认为曲柄是作匀速转动，所以ω一个参数确定了曲轴的运动状态。

2、活塞位移从图3一2可知，活塞位移：Χ=ΑΑ=ΑΟ−ΑΟ=ΑΟ−ΑC−CO=r+L−r cosα−L cosβ=r1+1λ−cosα+1λcosβ由上式知，位移x与r有关，不同型号的汽车发动机r是不一样的，为了便于比较分析不同大小汽车发动机活塞位移变化规律，常引用无量纲位移（又称位移系数）χ=χr，即用χ与r的相对值表示变化规律。