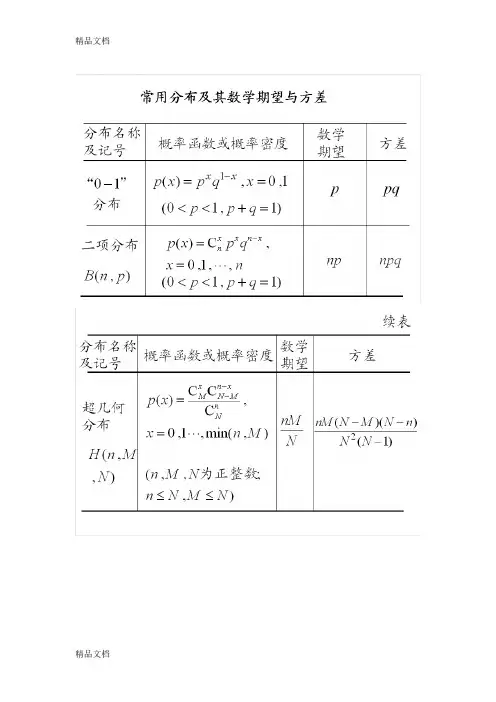
3-5某些常用分布的数学期望与方差
- 格式:ppt
- 大小:852.00 KB
- 文档页数:25

![[化学反应工程原理]第十章__停留时间分布-数学期望及方差](https://uimg.taocdn.com/7b781c5465ce0508763213e1.webp)




【关键字】学习《概率论与数理统计》学习指导·内容提要·疑难分析·例题解析·自测试题安徽工业大学应用数学系编目录第三章多维随机变量及其分布内容提要1、二维随机变量及其联合分布函数设,为随机变量,则称它们的有序数组()为二维随机变量.设()为二维随机变量,对于任意实数、,称二元函数为()的联合分布函数.联合分布函数具有以下基本性质:(1)是变量或的非减函数;(2)且;(3)关于右连续,关于也右连续;(4)对任意点,若,则.上式表示随机点落在区域内的概率为:.2、二维离散型随机变量及其联合分布律如果二维随机变量所有可能取值是有限对或可列对,则称为二维离散型随机变量.设为二维离散型随机变量,它的所有可能取值为将或表3.1称为的联合分布律.表3.1联合分布律具有下列性质:(1);(2).3、二维连续型随机变量及其概率密度函数如果存在一个非负函数,使得二维随机变量的分布函数对任意实数有,则称是二维连续型随机变量,称为的联合密度函数(或概率密度函数).联合密度函数具有下列性质:(1)对一切实数,有;(2);(3)在任意平面域上,取值的概率;(4)如果在处连续,则.4、二维随机变量的边缘分布设为二维随机变量,则称,分别为关于和关于的边缘分布函数.当为离散型随机变量,则称分别为关于和关于的边缘分布律.当为连续型随机变量,则称分别为关于和关于的边缘密度函数.5、二维随机变量的条件分布(1)离散型随机变量的条件分布设为二维离散型随机变量,其联合分布律和边缘分布律分别为),2,1,(}{,}{,},{.. ========j i p y Y P p x X P p y Y x X P j j i i ij j i ,则当j 固定,且0}{.>==j j p y Y P 时,称,2,1,}{},{}|{.========i p p y Y P y Y x X P y Y x X P jij j j i j i 为j y Y =条件下随机变量X 的条件分布律.同理,有 ,2,1,}|{.====j p p x X y Y P i ij i j(2)连续型随机变量的条件分布设),(Y X 为二维连续型随机变量,其联合密度函数和边缘密度函数分别为:)(),(),,(y p x p y x p Y X .则当0)(>y p Y 时,在),(y x p 和)(x p X 的连续点处,),(Y X 在条件y Y =下,X 的条件概率密度函数为:)(),()|(|y p y x p y x p Y Y X =.同理,有)(),()|(|x p y x p y x p X X Y =. 6、随机变量的独立性设),(y x F 及)()(y F x F Y X 、分别是),(Y X 的联合分布函数及边缘分布函数.如果对任何实数y x ,有)()(),(y F x F y x F Y X ⋅=则称随机变量X 与Y 相互独立.设),(Y X 为二维离散型随机变量,X 与Y 相互独立的充要条件是),2,1,(.. ==j i p p p j i ij . 设),(Y X 为二维连续型随机变量,X 与Y 相互独立的充要条件是对任何实数y x ,,有)()(),(y p x p y x p Y X =.7、两个随机变量函数的分布设二维随机变量),(Y X 的联合概率密度函数为),(y x p ,),(Y X Z ϕ=是Y X ,的函数,则Z 的分布函数为dxdy y x p z F zy x Z ⎰⎰=≤),(),()(ϕ.(1)Y X Z +=的分布若),(Y X 为离散型随机变量,联合分布律为ij p ,则Z 的概率函数为: ∑-=ii k i k Z x z x p z P ),()(或∑-=jj k j k Z y z y p z P ),()(.若),(Y X 为连续型随机变量,概率密度函数为),(y x p ,则Z 的概率函数为:dy y y z p dx x z x p z p Z ⎰-=⎰-=+∞∞-+∞∞-),(),()(.(2)YXZ =的分布 若),(Y X 为连续型随机变量,概率密度函数为),(y x p ,则Z 的概率函数为:⎰=+∞∞-dy y yz p y z p Z ),()(.疑 难 分 析1、事件},{y Y x X ≤≤表示事件}{x X ≤与}{y Y ≤的积事件,为什么},{y Y x X P ≤≤不一定等于}{}{y Y P x X P ≤⋅≤?如同仅当事件B A 、相互独立时,才有)()()(B P A P AB P ⋅=一样,这里},{y Y x X P ≤≤依乘法原理}|{}{},{x X y Y P x X P y Y x X P ≤≤⋅≤=≤≤.只有事件}{x X P ≤与}{y Y P ≤相互独立时,才有}{}{},{y Y P x X P y Y x X P ≤⋅≤=≤≤,因为}{}|{y Y P x X y Y P ≤=≤≤.2、二维随机变量),(Y X 的联合分布、边缘分布及条件分布之间存在什么样的关系?由边缘分布与条件分布的定义与公式知,联合分布唯一确定边缘分布,因而也唯一确定条件分布.反之,边缘分布与条件分布都不能唯一确定联合分布.但由)|()(),(|x y p x p y x p X Y X ⋅=知,一个条件分布和它对应的边缘分布,能唯一确定联合分布.但是,如果Y X 、相互独立,则}{}{},{y Y P x X P y Y x X P ≤⋅≤=≤≤,即)()(),(y F x F y x F Y X ⋅=.说明当Y X 、独立时,边缘分布也唯一确定联合分布,从而条件分布也唯一确定联合分布. 3、两个随机变量相互独立的概念与两个事件相互独立是否相同?为什么?两个随机变量Y X 、相互独立,是指组成二维随机变量),(Y X 的两个分量Y X 、中一个分量的取值不受另一个分量取值的影响,满足}{}{},{y Y P x X P y Y x X P ≤⋅≤=≤≤.而两个事件的独立性,是指一个事件的发生不受另一个事件发生的影响,故有)()()(B P A P AB P ⋅=.两者可以说不是一个问题.但是,组成二维随机变量),(Y X 的两个分量Y X 、是同一试验E 的样本空间上的两个一维随机变量,而B A 、也是一个试验1E 的样本空间的两个事件.因此,若把“x X ≤”、“y Y ≤”看作两个事件,那么两者的意义近乎一致,从而独立性的定义几乎是相同的.例 题 解 析例 1 设某班车起点站上的乘客数X 服从参数为)0(>λλ的泊松分布,每位乘客中途下车的概率为)10(<<p p ,且中途下车与否相互独立,以Y 表示中途下车的人数,求二维随机变量),(Y X 的分布律.解例2 设随机变量),(Y X 的概率密度为 试求(1)系数c ;(2)),(Y X 落在圆)0(222R r r y x <<≤+内的概率.解 所以 33Rc π=(2) 设{},:,222r y x y)(x D ≤+=注: 利用分布函数的基本性质可以确定待定系数,从而可以计算二维随机变量落在某一区域内的概率,值得注意的是计算过程中,由于),(y x f 通常是分区域函数,故积分区域要特别小心,以免出错.例3 考虑一元二次方程02=++C Bx x ,其中C B ,分别是将一枚骰子接连掷两次先后出现的点数,求该方程有实根的概率p 和有重根的概率q .解 方程02=++C Bx x 有实根的充要条件是判别式042≥-=∆C B 或4/2B C ≤,由条件知,0+1+2+4+6+6=19所以36/19=p ,使方程有重根的充要条件是C B 42=,满足此条件的基本事件个数为0+1+0+1+0+0=2因此 18/136/2==q例4 设随机变量),(Y X 均匀分布于以)1,0(),0,1(),1,0(),0,1(--四项点所构成的正方形中,求X 与Y 的边缘密度函数.解1º当01<<x -时,⎰+==⎰=+--∞∞-11121),()(x x X x dy dy y x f x f当10<≤x 时,121),()(11+-=⎰=⎰=+--∞∞-x dy dy y x f x f x x X 所以2º类似1º可得例5 随机变量),(Y X 的密度函数为⎪⎩⎪⎨⎧>>++= 其它,00,0,)1/(2),(3y x y x y x p ,求1=X 条件下Y 的条件分布密度.分析:通过),(Y X 的联合密度和边缘密度函数,来求在1=X 条件下Y 条件分布密度.解:当0>x 时,有203)1/(1)1/(2)(x dy y x x p X +=⎰++=∞,故 .例6 在),0(a 线段上任意抛两个点(抛掷二点的位置在),0(a 上独立地服从均匀分布),试求两点间距离的分布函数.解 设抛掷两点的坐标分别为X 和Y ,则X 与Y 相互独立,且都服从)(a ,0上的均匀分布,故),(Y X 的联合概率密度为记两点距离为Z ,则||Y X Z -=的分布函数为 )|(|)(z Y X P z F Z ≤-=当0<z 时,显然0)(=z F Z ; 当a z <≤0时,当a z ≥时,1)(=z F Z 故两点距离Z 的分布函数为例7 假设一电路装有三个同种电气元件,其工作状态相互独立,且无故障时间都服从参数为0>λ的指数分布,当三个元件都无故障时,电路正常工作,否则整个电路不能正常工作,试求电路正常工作的时间T 的概率分布.解 设)3,2,1(=i X i 为第i 个电子元件无故障工作的时间,则321,,X X X 是独立同分布的随机变量,其分布函数为记)(t G 为了T 的分布函数,则 当0<t ,0)(=t G ; 当0≥t 时,所以 ⎪⎩⎪⎨⎧<≥-=λ-0,00,1)(3t t e t G t即电路正常工作时间T 服从参数为λ3的指数分布.例8 设随机变量X 与Y 独立同分布,其概率密度为 求随机变量22Y X Z +=的概率密度.解 由于X 与Y 独立同分布,故),(Y X 的联合概率密度为当0≤z 时,显然0)(=z F Z 当0>z 时,故22Y X Z +=的概率密度为例9.已知随机变量1}2/1{,4/34/110~=-=⎥⎦⎤⎢⎣⎡Y P X ,又n 维向量123,,a a a 线性无关。

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载期望-方差公式-方差和期望公式地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容期望与方差的相关公式-、数学期望的来由早在17世纪,有一个赌徒向法国著名数学家帕斯卡挑战,给他出了一道题目,题目是这样的:甲乙两个人赌博,他们两人获胜的机率相等,比赛规则是先胜三局者为赢家,赢家可以获得100法郎的奖励。
当比赛进行到第三局的时候,甲胜了两局,乙胜了一局,这时由于某些原因中止了比赛,那么如何分配这100法郎才比较公平?用概率论的知识,不难得知,甲获胜的概率为1/2+(1/2)*(1/2)=3/4,或者分析乙获胜的概率为(1/2)*(1/2)=1/4。
因此由此引出了甲的期望所得值为100*3/4=75法郎,乙的期望所得值为25法郎。
这个故事里出现了“期望”这个词,数学期望由此而来。
定义1 若离散型随机变量可能取值为(=1,2,3 ,…),其分布列为(=1,2,3,…),则当<时,则称存在数学期望,并且数学期望为E=,如果=,则数学期望不存在。
定义2 期望:若离散型随机变量ξ,当ξ=xi的概率为P(ξ=xi)=Pi (i=1,2,…,n,…),则称Eξ=∑xi pi为ξ的数学期望,反映了ξ的平均值.期望是算术平均值概念的推广,是概率意义下的平均.Eξ由ξ的分布列唯一确定.二、数学期望的性质(1)设C是常数,则E(C)=C 。
(2)若k是常数,则E(kX)=kE(X)。
(3)。
方差的定义前面我们介绍了随机变量的数学期望,它体现了随机变量取值的平均水平,是随机变量一个重要的数字特征。
但是在一些场合下,仅仅知道随机变量取值的平均值是不够的,还需要知道随机变量取值在其平均值附近的离散程度,这就是方差的概念。

《概率论与数理统计》(双语)教学大纲学时:68学时学分:4分理论学时:68学时适用专业:计算机科学与技术专业大纲执笔人:郭大伟大纲审定人:祝东进一、说明:1、课程的性质,地位和任务概率论与数理统计是研究随机现象的一门数学学科,它已广泛地应用于工农业生产和科学技术之中,并与其它数学分支互相渗透与结合。
本课程是高等师范院校和综合性大学计算机科学与技术专业的一门重要基础课程,它的任务是使学生获得概率论的有关概念,一些初等概率的求法,离散型和连续型随机变量的定义和性质,随机变量的数字特征, 掌握参数估计和假设检验的基本原理和方法,熟悉方差分析和回归分析的实施过程。
2、课程教学的基本要求(1)掌握事件的关系及性质,概率的统计定义和概率的公理化定义,概率的性质及运算法则,熟悉古典概型和几何概型的解法。
(2)了解离散型和连续型随机变量的定义及性质,掌握一些常用分布和相关计算以及它们之间的关系,学会求随机变量的函数的分布,了解多维随机变量的定义及性质。
(3)掌握随机变量的数字特征的概念,重点了解数学期望和方差的意义,熟悉一些常用分布的数字特征,掌握大数定律和中心极限定理。
(4)了解总体,样本,统计量,估计的优良性,假设检验的原理等基本概念。
掌握统计量的分布,关于正态总体的检验方法。
(5)了解方差分析和回归分析的基本原理,熟悉单因素方差分析和二因素方差分析的方法,了解回归分析的数学模型和统计分析的方法。
3、教学目标通过本课程的教学,力求达到下列目标:(1) 深刻理解《概率论与数理统计》课程的特点,掌握其基本概念、理论与方法,掌握建立统计模型处理随机现象的思想和方法,掌握该课程基本专业英语的听、读和写。
(2) 通过具体的概率统计模型,培养学生运用所学专业知识发现并分析解决实际问题的能力。
(3) 通过课程实验,做到与计算机科学与技术专业人才培养目标的紧密结合,培养掌握坚实数学基础的计算机类综合型人才。
4、课程教学改革注重理论联系实际,提高学生从日常生活和科学研究的实践中应用统计方法的能力。
