常见分布的期望与方差的计算

常见分布的期望与方差的计算期望和方差是描述概率分布特征的重要统计量。

在统计学中，期望是对一个随机变量的全体取值的加权平均，而方差则是每个随机变量观察值与期望之间差异的平方的平均。

在本文中，我们将讨论几个常见分布的期望和方差的计算方法。

1.二项分布：二项分布用于描述多次独立的二元试验中成功次数的概率分布。

假设随机变量X服从二项分布B(n,p)，其中n为试验次数，p为每次试验成功的概率。

那么其期望和方差分别为：期望：E(X) = np方差：Var(X) = np(1-p)2.泊松分布：期望：E(X)=λ方差：Var(X) = λ3.正态分布：正态分布是最为常见的连续型概率分布，许多自然现象都可以近似地用正态分布来描述。

假设随机变量X服从正态分布N(μ,σ^2)，其中μ为均值，σ^2为方差。

那么其期望和方差分别为：期望：E(X)=μ方差：Var(X) = σ^24.均匀分布：均匀分布用于描述在一个区间内取值概率相等的随机变量。

假设随机变量X服从均匀分布U(a,b)，其中a为最小值，b为最大值。

那么其期望和方差分别为：期望：E(X)=(a+b)/2方差：Var(X) = (b-a)^2/125.几何分布：几何分布用于描述独立重复进行的同一事件中首次成功所需的次数的概率分布，例如投掷硬币直到出现正面的次数。

假设随机变量X服从几何分布Geo(p)，其中p为每次试验成功的概率。

那么其期望和方差分别为：期望：E(X)=1/p方差：Var(X) = (1-p)/(p^2)以上是几个常见分布的期望和方差的计算方法。

通过了解和计算概率分布的期望和方差，我们可以更好地理解和描述随机变量的特点，从而进行更准确的统计分析和推断。

高中数学中的概率统计应用概率分布计算期望与方差的技巧概率统计是高中数学的重要内容之一，其应用广泛且重要。

在概率统计中，我们经常遇到需要计算随机变量的期望和方差的问题。

概率分布是解决这些问题的关键工具之一。

在本文中，我们将介绍一些高中数学中常见的概率分布，以及计算期望和方差的技巧。

1. 离散概率分布离散概率分布指的是随机变量只能取有限个或可列个值的概率分布。

其中，最常见的离散概率分布有二项分布、泊松分布和几何分布。

1.1 二项分布二项分布在实际问题中经常出现，特别是在重复试验的情况下。

假设有n个独立的重复试验，每次试验有成功和失败两种可能结果。

如果成功的概率为p，失败的概率为q=1-p，则随机变量X表示n次试验中成功的次数。

二项分布的概率密度函数为：P(X=k) = C(n,k) * p^k * q^(n-k)其中，C(n,k)表示组合数。

二项分布的期望和方差的计算公式如下：E(X) = npVar(X) = npq1.2 泊松分布泊松分布适用于描述单位时间或空间内随机事件发生的次数。

例如，某地区每小时的交通事故数、每天接到的电话数等。

泊松分布的概率密度函数为：P(X=k) = (λ^k * e^(-λ)) / k!其中，λ代表单位时间或单位空间内平均发生的次数。

泊松分布的期望和方差的计算公式如下：E(X) = Var(X) = λ1.3 几何分布几何分布用于描述一系列独立重复试验中，首次成功所需的试验次数。

例如，投掷一枚硬币直到首次出现正面的次数等。

几何分布的概率密度函数为：P(X=k) = q^(k-1) * p其中，p表示成功的概率，q=1-p表示失败的概率。

几何分布的期望和方差的计算公式如下：E(X) = 1/pVar(X) = q/(p^2)2. 连续概率分布连续概率分布指的是随机变量可以取某个区间内的任意值的概率分布。

最常见的连续概率分布有均匀分布、正态分布和指数分布。

2.1 均匀分布在均匀分布中，随机变量在某一区间内的取值是等可能的。

超几何分布和二项分布的期望和方差公式
超几何分布和二项分布是两种常见的概率分布，分别用于描述随机实验中某种结果出现的次数。

下面是超几何分布和二项分布的期望和方差公式：超几何分布：
期望：E(X) = n * p
方差：Var(X) = n * p * (1 - p)
其中，n 是随机实验的次数，p 是某种结果出现的概率。

二项分布：
期望：E(X) = n * p
方差：Var(X) = n * p * (1 - p)
其中，n 是随机实验的次数，p 是某种结果出现的概率。

注意，超几何分布和二项分布的期望和方差公式是相同的。

这是因为它们的概率分布函数都是二项分布函数的一种形式。

不过，超几何分布通常用于描述在一系列独立随机实验中，某种结果出现的次数，而二项分布则常用于描述成功/失败类型的随机实验。

概率计算中的期望与方差计算概率计算是数学中的一个重要分支，广泛应用于各个领域，包括金融、统计学、物理学等。

在概率计算中，期望与方差是两个基本的概念和工具，用于描述随机变量的特征和分布。

本文将详细介绍期望与方差的计算方法及其应用。

一、期望的计算期望是随机变量的平均值，它可以理解为对随机变量进行大量重复实验后的平均结果。

期望的计算公式如下：E(X) = Σ[x * P(x)]其中，E(X)表示随机变量X的期望，x表示随机变量可能取到的值，P(x)表示该值发生的概率。

以掷骰子为例，假设骰子是均匀的，即各个面出现的概率相等。

骰子的期望可以通过以下计算得出：E(X) = 1 * 1/6 + 2 * 1/6 + 3 * 1/6 + 4 * 1/6 + 5 * 1/6 + 6 * 1/6 = 3.5这意味着在长期的掷骰子实验中，每次掷出的点数的平均值接近于3.5。

二、方差的计算方差衡量的是随机变量离其期望的平均偏离程度，用于描述随机变量的分散程度。

方差的计算公式如下：Var(X) = Σ[(x - E(X))^2 * P(x)]其中，Var(X)表示随机变量X的方差，x表示随机变量可能取到的值，E(X)表示随机变量X的期望，P(x)表示该值发生的概率。

继续以掷骰子为例，我们计算骰子的方差：Var(X) = [(1-3.5)^2 * 1/6] + [(2-3.5)^2 * 1/6] + [(3-3.5)^2 * 1/6] + [(4-3.5)^2 * 1/6] + [(5-3.5)^2 * 1/6] + [(6-3.5)^2 * 1/6] = 2.92从结果可以看出，骰子的结果相对稳定，方差较小。

三、期望与方差的应用期望和方差作为概率计算的基本工具，应用广泛。

以下是一些常见的应用场景：1. 金融领域：在金融建模中，期望和方差被广泛应用于资产收益的预测和风险评估。

投资者可以通过计算期望和方差来评估投资组合的预期收益和风险。

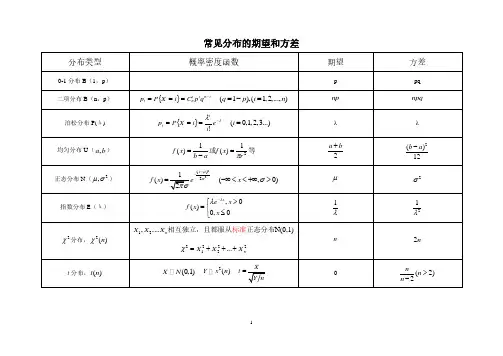
常见的概率分布离散分布0-1分布(伯努利分布)它的分布律为：\[P\{X=k\}=p^k(1-p)^{1-k}, k=0,1, (0<p<1)\]0-1分布记作：\(X \sim b(1,p)\)期望：\(E(X)=p\)⽅差:\(D(X)=p(1-p)\)常⽤的场景：新⽣婴⼉性别的登记，招⽣考试的录取，产品的是否合格，硬币的正反⾯。

⼆项分布⼆项分布为\(n\)重伯努利实验的概率分布。

分布律为：\[P\{X=k\}=\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k},k=0,1,2,...,n,(0<p<1)\]\[\sum\limits_{k=0}^{n}P\{X=k\}=\sum\limits_{k=0}^{n}\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}=(p+1-p)^n=1\]⼆项分布记作：\( X \sim b(n,p)\)期望：\(E(X)=np\)⽅差:\(D(X)=np(1-p)\)常⽤的场景：⽐如⼀个⼈射击\(n\)次，其中\(k\)次命中的概率，抽查50台设备，其中10台出故障的概率等等。

从下⾯的图中，我们可以看到命中次数先增加，到了3达到最⼤，之后⼜逐渐减少，⼀般来说，对于固定的\(n,p\)，都具有这⼀性质。

（1）当\(（n+1）p\)不为整数时，⼆项概率\(P\{X=k\}\)在\(k=[(n+1)p]\)时达到最⼤值；（2）当\(（n+1）p\)为整数时，⼆项概率\(P\{X=k\}\)在\(k=(n+1)p,k=(n+1)p-1\)时达到最⼤值。

%每轮射击10次，命中概率0.3，射击10000轮，x中返回的是每轮中命中的次数x=binornd(10,0.3,10000,1);%bin的数⽬为10hist(x,10);N=100;p=0.4;k=0:N;%事件发⽣k次的概率pdf=binopdf(k,N,p);%事件发⽣不⼤于k次的概率cdf=binocdf(k,N,p);plotyy(k,pdf,k,cdf);grid on;多项分布多项式分布是⼆项式分布的扩展，在多项式分布所代表的实验中，⼀次实验会有多个互斥结果，⽽⼆项式分布所代表的实验中，⼀次实验只有两个互斥结果。

概率分布期望方差汇总概率分布是描述随机变量取值的概率的数学模型。

期望是对随机变量取值的平均值的度量，方差则是衡量随机变量取值分散程度的度量。

在概率论和统计学中，期望和方差是两个重要的概念，对于理解和应用概率分布非常关键。

一、期望期望是对随机变量取值的平均值的度量，也可以理解为随机变量的中心位置。

对于离散随机变量X，其期望计算公式为E(X) = Σ x*p(x)，即随机变量各取值乘以其对应的概率之和。

对于连续随机变量X，其期望计算公式为E(X) = ∫ x*f(x) dx，其中f(x)是X的概率密度函数。

二、方差方差是对随机变量取值分散程度的度量。

方差越大，表示随机变量的取值更分散；方差越小，表示随机变量的取值更集中。

方差计算公式为Var(X) = E[(X-E(X))^2]，即随机变量取值与其期望之差的平方的期望。

方差的平方根称为标准差。

三、常见概率分布的期望和方差1.二项分布二项分布是最常见的离散概率分布之一，描述在n次独立重复试验中成功次数的分布。

设X为成功次数，则X服从参数为n和p的二项分布记作X~B(n,p)。

期望：E(X) = np方差：Var(X) = np(1-p)2.泊松分布泊松分布描述单位时间或单位空间内事件发生的次数的概率。

设X为单位时间或单位空间内事件发生的次数，则X服从参数为λ的泊松分布记作X~P(λ)。

期望：E(X)=λ方差：Var(X) = λ3.均匀分布均匀分布是最简单的连续概率分布之一，描述在一个区间上随机取值的概率。

设X在[a,b]区间上服从均匀分布，则X服从均匀分布记作X~U(a,b)。

期望：E(X)=(a+b)/2方差：Var(X) = (b-a)^2/124.正态分布正态分布是最常见的连续概率分布之一，其概率密度函数呈钟型曲线。

设X服从参数为μ和σ^2的正态分布记作X~N(μ,σ^2)。

期望：E(X)=μ方差：Var(X) = σ^25.指数分布指数分布描述连续随机事件发生的时间间隔的概率。

欢迎下载 2概率与数理统计重点摘要1、正态分布的计算：()()()X F x P X x μσ-=≤=Φ。

2、随机变量函数的概率密度：X 是服从某种分布的随机变量，求()Y f X =的概率密度：()()[()]'()Y X f y f x h y h y =。

（参见P66～72）3、分布函数(,)(,)x yF x y f u v dudv -∞-∞=⎰⎰具有以下基本性质：⑴、是变量x ，y 的非降函数；⑵、0(,)1F x y ≤≤，对于任意固定的x ，y 有：(,)(,)0F y F x -∞=-∞=；⑶、(,)F x y 关于x 右连续，关于y 右连续；⑷、对于任意的11221212(,),(,),,x y x y x x y y << ，有下述不等式成立：22122111(,)(,)(,)(,)0F x y F x y F x y F x y --+≥4、一个重要的分布函数：1(,)(arctan )(arctan )23x y F x y πππ2=++22的概率密度为：22226(,)(,)(4)(9)f x y F x y x y x y π∂==∂∂++5、二维随机变量的边缘分布：边缘概率密度：()(,)()(,)X Y f x f x y dy f y f x y dx+∞-∞+∞-∞==⎰⎰边缘分布函数：()(,)[(,)]()(,)[(,)]x X y Y F x F x f u y dy duF y F y f x v dx dv+∞-∞-∞+∞-∞-∞=+∞==+∞=⎰⎰⎰⎰ 二维正态分布的边缘分布为一维正态分布。

6、随机变量的独立性：若(,)()()X Y F x y F x F y =则称随机变量X ，Y 相互独立。

简称X 与Y 独立。

欢迎下载 37、两个独立随机变量之和的概率密度：()()()()()Z X Y Y X f z f x f z x dx f y f z y dy +∞+∞-∞-∞=-=-⎰⎰其中Z ＝X ＋Y8、两个独立正态随机变量的线性组合仍服从正态分布，即22221212(,Z aX bY N a b a b μμσσ=+++):。

罕有散布的期望和方差(0,1)N 2()Yx n t =概率与数理统计重点摘要1.正态散布的盘算：()()()X F x P X x μσ-=≤=Φ.2.随机变量函数的概率密度：X 是屈服某种散布的随机变量,求()Y f X =的概率密度：()()[()]'()Y X f y f x h y h y =.（拜见P66～72）3.散布函数(,)(,)xyF x y f u v dudv -∞-∞=⎰⎰具有以下基赋性质：⑴.是变量x,y 的非降函数;⑵.0(,)1F x y ≤≤,对于随意率性固定的x,y 有：(,)(,)0F y F x -∞=-∞=; ⑶.(,)F x y 关于x 右持续,关于y 右持续;⑷.对于随意率性的11221212(,),(,),,x y x y x x y y << ,有下述不等式成立：4.一个主要的散布函数：1(,)(arctan )(arctan )23x y F x y πππ2=++22的概率密度为：22226(,)(,)(4)(9)f x y F x y x y x y π∂==∂∂++ 5.二维随机变量的边沿散布：边沿概率密度：()(,)()(,)X Y f x f x y dyf y f x y dx+∞-∞+∞-∞==⎰⎰边沿散布函数：()(,)[(,)]()(,)[(,)]xX yY F x F x f u y dy du F y F y f x v dx dv+∞-∞-∞+∞-∞-∞=+∞==+∞=⎰⎰⎰⎰二维正态散布的边沿散布为一维正态散布.6.随机变量的自力性：若(,)()()X Y F x y F x F y =则称随机变量X,Y 互相自力.简称X 与Y 自力.7.两个自力随机变量之和的概率密度：()()()()()Z X Y Y X f z f x f z x dx f y f z y dy +∞+∞-∞-∞=-=-⎰⎰个中Z ＝X ＋Y8.两个自力正态随机变量的线性组合仍屈服正态散布,即22221212(,Z aX bY N a b a b μμσσ=+++). 9.期望的性质：……（3）.()()()E X Y E X E Y +=+;（4）.若X,Y 互相自力,则()()()E XY E X E Y =. 10.方差：22()()(())D X E X E X =-.若X,Y不相干,则()()()D X Y D X D Y +=+,不然()()()2(,)D X Y D X D Y Cov X Y +=++,()()()2(,)D X Y D X D Y Cov X Y -=+-11.协方差：(,)[(())(())]Cov X Y E X E X Y E Y =--,若X,Y 自力,则(,)0Cov X Y =,此时称：X 与Y 不相干. 12.相干系数：(,)()()XY Cov X Y X Y ρσσ==1XY ρ≤,当且仅当X 与Y 消失线性关系时1XY ρ=,且1,b>0;1,b<0XY ρ⎧=⎨-⎩ 当 当。