当前位置：文档之家 › 23极限的性质及运算法则

23极限的性质及运算法则

  • 格式：ppt
  • 大小：198.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

微积分2.3 函数极限的性质及运算法则

微积分2.3 函数极限的性质及运算法则

x→ A x→ X
lim f [ g ( x ) ] =
x→ X
令g ( x ) = y
lim f ( y ) = B .
y→ A
变量替换法 这一性质是用变量替换求极限的理论基础
例
证明: lim 证明: f ( x ) = 0 的充要条件是 lim f ( x ) = 0.
x→ X x→ X
必要性: 证明 必要性: 变量替换求极限
lim f ( x )
x→ X →
y = f ( x)
lim y = 0,
y →0
充分性: 充分Leabharlann :由于 f ( x ) ≤ f ( x ) ≤ f ( x )
根据夹逼定理可得 lim f ( x ) = 0.
x→ X
如果存在求出其值: 例 判别下列极限是否存在 ,如果存在求出其值: (1) lim 2 ; ( 2) lim e ; ( 3) lim e
x→ X
lim [ f ( x ) ± g ( x )] = lim f ( x ) ± lim g ( x ) = A ± B;
x→ X x→ X
x→ X
lim [ f ( x ) g ( x )] = lim f ( x ) lim g ( x ) = AB;
x→ X x→ X
lim f ( x ) x→ X f ( x ) A lim (这里要求 B ≠ 0). = = x→ X g( x ) lim g ( x ) B
2x + 7 3 ( 3) lim 3 . x →1 x 1 m key : ;4;1. n
P43/2(1,2)
x3 + ax2 x + 4 2.设lim 有 限 限 l,求 ,l. 有 极 值 a x→ 1 x +1 a = 4,l =10.
23_函数极限性质4解读

23_函数极限性质4解读


(1)重要极限 lim
sin x 1 x 0 x 由右图可知： S AOB S扇形AOB S AOD ,
B
D
x AB
sin x CB
1 1 1 sin x x tan x , 2 2 2 sin x x tan x,
O
x
tan x AD C A
不等号各边都除以sin x得, x 1 sin x 1 , 或 cos x 1. sin x cos x x
| f ( x ) | M , (x O( x0 ) \ { x0 }).
性质3(局部保号性) 假设 lim f ( x ) A，lim g( x ) B
x x0 x x0
(1)如 A B( B )，则对 x0 的某一去心邻域中的所有 x， 有
f ( x ) g( x )( g( x ))。
由此看来极限 A与 f ( x0 )毫无关系，A 的存在与否 及大小与f ( x0 )的大小甚至f ( x0 )有无定义都无关系.
我们称函数f ( x )在某点 x0的邻域内（或除去x0）的性质 为函数的局部性质.
1.函数极限的性质 性质1 (函数极限的唯一性)假设在同一极限过程中有
x x0
lim f ( x ) A, 和 lim f ( x ) B, 则 A B。
x x0
运算法则有
P ( x ) P ( x0 ) lim . x x0 Q ( x ) Q ( x0 )
但若Q( x0 ) 0，则关于商的极限的运算法则不能应用。
定理 2：（复合函数的极限运算法则）若 lim g( x ) A,
x x0
且g ( x ) A(这里A可以是无穷大 ), lim f ( u) B , 则
极限的运算法则

极限的运算法则

定义 如果对于任意给定的正数E,变量y在 其变化过程中,总有那么一个时刻, 在那个 时刻以后,不等式
|y|>E 恒成立,则称变量y是该变化过程中的无穷 大量,或称变量y 趋于无穷大,记作limy=
注意：(1)无穷大是变量,不是很大的数
(2)无穷大的函数其极限是不存在
即 勿将 lim f (x) 认为极限存在. xx0
lim
2
=0
x x 2 x
题 求 lim
x2
x0 1 1 x2
解
x2 lim
lim
x2 (1 1 x2 )
x0 1 1 x2 x0 (1 1 x2 )(1 1 x2 )
lim x2 (1 1 x2 )
x0
x2
2
例8

7. 3
x2
多项式
小结: 1. 设f(x)=a0xn+a1xn1+...+an ,则有
lim
x x0
f
(
x
)

a0
(
lim
x x0
x)n

a1
(
lim
x x0
x)n1 an
=a0x0n+a1x0n1+...+an =f(x0)
有理分式
2.设
f (x)
P( Q(
x) x)
A
B
A B

A B
B A B(B )
∵BA 0, |B+ |≥|B|| |
又∵ 0
>0,在变量的变化过程中,总有那么
一个时刻,在那个时刻以后,||<成立
|B+ |≥|B|| | >|B|
极限的运算法则

极限的运算法则


lim(
n
1 n2
2 n2
n n2
)
lim
n
1
2
n2
n
1 n(n 1)
lim 2 n
n2
1 2
lim(1
n
n1 )
1. 2
目录
小结
------极限求法;
1.多项式与分母不为零的分式函数代入法求极限;
2.利用无穷小与无穷大的关系求 A型极限;
0
0
3.消去零因子法求 0极限;
4.分子分母同除以x的最高次方法求 (x 型) 极限; 5.通分法求 极限;
0
则来计算的极限
目录
*求未定式极限方法举例、练习 1. 0 型有理式 0
约零因子法（因 式分解）
方法：分子分母分解因式，消去使他们趋于
零的公因子
( 0型) 0
解
目录
x2 9 lim x3 x 3
解 分析：因为 lim（x2 9） 0，lim（x 3） 0.
x3
x3
lim x2 9 lim ( x 3)( x 3) lim( x 3) 6
lim[c f (x)] c lim f (x) （c为常数）
特例2：推广到有限个函数的积
3、除法法则: 商的极限等于极限的商
lim
f (x) g( x)
lim f (x)
lim g(x)
A B
（B 0）
小 结: 函数的和、差、积、商的极限等于函数极限
的和、差、积、商
目录
(1)和函数的极限等于极限的和. (2)积函数的极限等于极限的乘积. (3)商函数的极限等于极限的商(分母不为零).
lim
x
2 3
2.3 极限的运算法则

2.3 极限的运算法则


= lim =0 x→0 x( 1 + x + 1) x→0 ( 1+ x2 +1)
2
x2
x
7
2.3.2 无穷小量与无穷大量
一、无穷小量
在实际应用中，经常会遇到极限为 的变量 的变量。 在实际应用中，经常会遇到极限为0的变量。 对于这种变量不仅具有实际意义， 对于这种变量不仅具有实际意义，而且更具有理 论价值， 论价值，值得我们单独给出定义 的某一变化过程中,函数 极限为零,称 定义1: 的某一变化过程中 函数f(x)极限为零 定义 在x的某一变化过程中 函数 极限为零 称 f(x)为该过程的无穷小量（简称无穷小）. 为该过程的无穷小量（简称无穷小） 为该过程的无穷小量 无穷小 例如 : ∵ lim x = 0, ∴ 函 数 x是 当 x → 0时 的 无 穷 小.
§2.3 极限运算法则
本节讨论极限的求法。利用极限的定义， 本节讨论极限的求法。利用极限的定义，从变 量的变化趋势来观察函数的极限， 量的变化趋势来观察函数的极限，对于比较复杂的 函数难于实现。为此需要介绍极限的运算法则。 函数难于实现。为此需要介绍极限的运算法则。首 先来介绍极限四则运算法则。 先来介绍极限四则运算法则。
10
三、无穷小与无穷大的关系
定理3 在自变量的同一变化过程中, 定理3 在自变量的同一变化过程中, 1 为无穷大, 为无穷大, 则 若 为无穷小 ; f (x) 1 为无穷大. 为无穷大. 为无穷小, 若 为无穷小, 且f (x) ≠ 0, 则 f (x) 据此定理，关于无穷大的讨论,都可归结为 意义 据此定理，关于无穷大的讨论 都可归结为 关于无穷小的讨论. 关于无穷小的讨论 C 2x + 4 型 . 例6 求 lim 0 x→−1 x + 1 x +1 lim = 0 再利用无穷小与无穷大 之间的关系, 解 ∵ x → −1 再利用无穷 与无穷大 之间的关系, 无穷小 2x + 4 2x + 4 =∞ 可得: 可得: lim 11 x → −1 x + 1
2.3极限性质、法则

2.3极限性质、法则

x →0
(2) lim e
x →∞
(3) lim e
x→0
解：（1） ：（ ）
Q lim 2 +
x→0
1 x
1 y = x
y→+∞ →+∞
lim 2 y
= +∞
x→0
lim− 2
1 x
1 y = x
1 x
y→−∞ →−∞
lim 2
y
1 t = − y lim =0 t t →+∞ 2
∴ lim 2 不存在
令δ = min{δ 1 , δ 2 }, 则当x ∈ Oδ ( x0 ) \ { x0 }时有
A+ B g( x ) < < f ( x) 2
【2-3-3】
3、推论1： 、推论 ：
若 lim f ( x ) = A > B(或 < B ), 则∃δ > 0, 使得
x → x0
当x ∈ Oδ ( x0 ) \ { x0 }时, 有f ( x ) > B(或 < B )
即A − 1 < f ( x ) < A + 1, 所以f ( x )局部有界
【2-3-1】
二、局部保序性 1、定理： lim 、定理： 若
x → x0
f ( x ) = A, lim g( x ) = B , 且A > B , 则∃δ > 0,
x → x0
使得当x ∈ Oδ ( x0 ) \ { x0 }时, 有f ( x ) > g( x )
【2-3-5】
2、※证明： 、 证明：
x → x0
对 ∀ε > 0
Q lim g ( x ) = A,∴ ∃δ 1 > 0, 使当x ∈ Oδ 1 ( x0 ) \ { x0 }时,
极限的性质及运算法则

极限的性质及运算法则


去心邻域 在该邻域内 有f(x)0(或f(x)0) 定理3 如果在x0的某一去心邻域内f(x)0(或f(x)0)
而且 lim f(x)=A 那么 A0(或 A0)
x x0
推论 如果j(x)f(x) 而limj(x)=a limf(x)=b 那么ab
首页 上页 返回 下页 结束 铃
2x3 x2 5 lim = 2 2x 1 x 3x
•讨论
有理函数的极限 lim
a0 x n a1x n 1 an b0 xm b1 x m 1 bm
x
=?
•提示
0 0 a0 x n a1x n 1 an a0 a0 x n a1x n 1 an a0 lim lim = = m b x m 1 b m b x m 1 x b x x b x bm b b 0 0 1 1 m 0 0
当 Q ( x 0 ) = 0 且 P ( x 0 ) 0 时
lim
当Q(x0)=P(x0)=0时 约去分子分母的公因式(xx0)
首页
上页
返回
下页
结束
铃
3x3 4x2 2 例5 例 5 求 lim 3 5x 2 3 x 7 x
解 先用x3去除分子及分母 然后取极限
二、极限的四则运算法则
定理5 如果 lim f(x)=A lim g(x)=B 则 lim[f(x)g(x)] 存在 并且 lim[f(x)g(x)]=limf(x)limg(x)=AB lim f(x)g(x)=lim f(x)lim g(x)=AB lim [c f(x)]=c lim f(x) (c 为常数)
x 1 x 1 x 1 x 1
高等数学极限的运算法则与性质

高等数学极限的运算法则与性质


例1
求
lim
x2
x
2
x3 1 3x
5
.
解 lim( x 2 3x 5) lim x 2 lim 3x lim 5
x2
x2
x2
x2
(lim x)2 3 lim x lim 5
x2
x2
x2
22 3 2 5 3 0,
lim x2
x2
x3 1 3x
5
lim( x3 1)
x
a0 xm b0 xn
a1xm1 b1xn1
am bn
0,当n m,
,当n m,
7
首页
上页
返回
下页
结束
铃
例4
求
1
lim(
n
n
2
2 n2
n n2
).
解 n 时,是无限多个无穷小之和．
先变形再求极限.
1
lim(
n
n
2
2 n2
n n2
)
lim 1
n
2
n2
n
1 n(n 1)
lim 2
13
首页
上页
返回
下页
结束
铃
3. 函数极限的局部保号性
如果lim f (x) A, 且A 0(或A 0),那么 x x0
存在常数 0, 使得当0 x x0 时，有
f (x) 0(或f (x) 0).
14
首页
上页
返回
下页
结束
铃
问题讨论
思考题
在某个过程中，若 f ( x) 有极限，g( x) 无极限，那么f ( x) g( x)是否有极限？为
23性质与极限运算法则-精品文档

23性质与极限运算法则-精品文档


说明:
sin x 必须在 x 0 的过程中才 1 、使用公式 lim 1 时， x 0 x 2 sin x sin x lim ? 0 例如： lim ? x x x x 2
sin x ( 例如是 x 的函数 ) ， 2 、在 lim 中， 若 x 是一个其他的变量， x 0 x sin* 则 lim 1 仍成立 记作 * 那么如果满足下列两点 ， * 0 * (1)三个 *处是相同的；
x X
性质2.10 若 lim g ( x ) A （这里 A 可以是无穷
x X
且 g ( x ) A ， lim f( x ) B ,则 lim f[ g ( x )] B .
x A x X
这一性质是用变量替换求极限的理论基础，
x X
lim f [ g ( x ) ] lim f ( y ) B .
(2)*表示的变量必须是趋于 0 的。
sin 2 x 例 2 、求 lim x 0 sin 3 x
解:
0 0
sin2x 2x 2 sin 2 x 3 x 2 x lim lim lim ( ) x0 0 sin3x x 2 x sin 3 x3 x x0 3x 3
性质2.9
x X
若 lim f ( x ) A , lim g ( x ) B ，则
x X x X
x X
lim [ Cf ( x )] C lim f ( x ) CA ( C 是与 x 无关 ) ;
x X
lim [ f ( x ) g ( x )] lim f ( x ) lim g ( x ) A B ;
x X
极限过程 x X 所允许的某一邻域内有 界 . lim f(x )A , lim g (x ) 性质2.6 （局部保号性）若 x X x X
大学高数2-3极限的运算法则

大学高数2-3极限的运算法则


03
复合函数的极限运算法则
函数的极限与复合函数的极限
函数的极限
当函数在某点的自变量趋于某值时，函数值的极限。
复合函数的极限
对于复合函数$f(g(x))$，当$x$趋于某值时，$g(x)$趋于某值，则$f(g(x))$的极限存在。
复合函数的极限运算法则
乘法法则
若$f(x)$和$g(x)$在某点的极 限都存在，则$f(x) cdot g(x)$ 在该点的极限也存在，且$f(x) cdot g(x) = f(x) cdot g(x)$。
01
02
03
04
加法运算性质
两个无穷小量的和仍为无穷小 量。
减法运算性质
两个无穷小量的差仍为无穷小 量。
乘法运算性质
有限个无穷小量的乘积仍为无 穷小量。
除法运算性质
有限个无穷小量的商仍为无穷 小量，但除数不能为无穷大量 。
05
极限的运算技巧
利用等价无穷小替换求极限
等价无穷小替换是求极限的一种常用方法，通过将复杂的表达式替换为简单的无穷 小量，可以简化计算过程。
在等价无穷小替换中，常用的等价无穷小量包括：当x趋近于0时，sin x ≈ x，tan x ≈ x，e^x - 1 ≈ x，ln(1 + x) ≈ x等。
使用等价无穷小替换求极限时，需要注意替换的准确性和适用范围，以确保结果的 正确性。
利用洛必达法则求极限
01
02
03
洛必达法则是求极限的一种重要 法则，适用于0/0型和∞/∞型的 极限问题。
利用反常函数求极限
总结词
反常函数包括无界函数和无穷大量，求极限时需要注意函数的定义域和性质。
详细描述
对于无界函数和无穷大量，需要分别讨论其类型和性质，利用等价无穷小替换、夹逼准则等方法求极 限。在处理反常函数时，需要注意函数的定义域和性质，以及无穷小与无穷大的关系。
微积分23函数极限的性质及运算法则

微积分23函数极限的性质及运算法则


（类似可定义其他过程下的有界性）
性质2.5（局部有界li性 mf(） x)若 A,则f(x)在
xX
极限过 x 程X所允许的某一界邻 . 域内有
性质2.6（局部保号 lim 性 f(x） )A若 ,limg(x)
xX
xX
B, AB,则f(x)与g(x)在 极 限x过 X 程 所 允 许
解 x 时, 分母 , 分子 . “ 抓大头”
分子分母同除以 x 2 , 则
原式
lim431x 9x12
x
521x
1 x2

4 5
练习l： im 5 x3求 3x220 x x1
lim(x2)7 x2 x (2x 1)9

1 29
lim(x 2)2 x
故只 x 需 0 且 x 讨 0 的论 情 y 形 D 。
C
作单位圆，如右.图
设 AO xC (0x)
2
x
O A Bx
A s C x i,n B tD a x , n
O的 B C 扇 面 O的 形 积 B C 面 O的 B 积 ， D 面
1sin x1x1taxn
lim f(x)x l iX m f(x)A(这里B要 0).求 x Xg(x) lim g(x) B
x X
说明: 性质可推广到有限个函数的情形 .
应用极限四则 时运 ，算 要法 注则 意:使用条
(1)参加求极限的函数应为有限个; (2)每个函数的极限都必须存在;
(3)考虑商的极限时，还需要求分母的极限不为零。
, 当nm
此结论成立注意： (1)必须为 型!!!
(2)结论也可适m,用 n不于是正整数的情
复合函数求极限：

2(3)极限运算法则

7
极限运算法则
例7 求
12 1 lim 3 x →2 x 2 x 8
[∞ ∞]
先充分
例8 求 lim sin x 问:
有界函数 利用无穷 小的性质 x →∞ x ∞ sin x lim sin x 0 1. lim = x →0 = =1 ? x →0 x lim x 0 x →0 sin x lim sin x 2. lim = x →∞ =0 ? x →∞ x lim x
求 a, b.
18
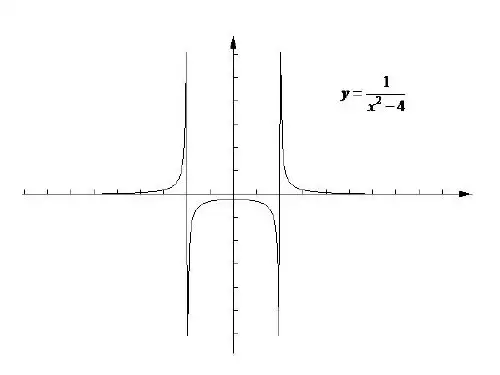
二,渐近线
1. 铅直渐近线
x → x0
(垂直于 轴的渐近线 垂直于x轴的渐近线) 垂直于 轴的渐近线
x → x0
如果 lim + f ( x ) = ∞ 或 lim f ( x ) = ∞
那么 x = x0就是y = f ( x ) 的一条 铅直渐近线 铅直渐近线.
2. 水平渐近线
x → x0 u→ u0
当x ∈ U ( x0 , δ 0 )时,
有 g(x) ≠u0,
则
u = g ( x) x → x0时, === lim f [ g ( x)] lim f [u ] = A x → x0 u →u0 u → u0
u ≠ u0
13
极限运算法则
注意:
条件: 当x ∈ U ( x0 , δ 0 )时, 有 g(x) ≠u0, 很重要,否则结论不成立.
x2 1 2 2 1 = 2 < 2, 时, 证 注意 当x > 0时 有 x 2 1 x +1 x + 2 x2 1 ε > 0,为了使 2 1 < ε, 只要使 2 < ε, x +1 x
x 解出 2 2 , 取G = , 当x > G时 有 即 x> , ε ε x2 1 x2 1 2 所以 lim 2 = 1. 1 < 2 < ε 2 x →+∞ x + 1 x +1 x x2 1 从而 y = 2 有水平渐近线y = 1. x +1

1_2_3 极限的性质与运算 高等数学 微积分 考研数学


再利用后一极限式 , 得
可见
3 lim f (x) lim (a b)
x0 x
x0
x
故
Page 18
型
,
约去公因子
3) x 时 , 分子分母同除最高次幂 “ 抓大头”
(2) 复合函数极限求法
设中间变量
Page 15
思考及练习
1.
问
是否存在 ? 为什么 ?
答: 不存在 . 否则由 利用极限四则运算法则可知 矛盾.
存在 , 与已知条件
2.
解:
原式
lim
n
n (n 1) 2n2
lim 1 (1 n 2
Page 6
定理 4 . 若 lim f (x) A, lim g(x) B , 且 B≠0 , 则有
证: 因 lim f (x) A, lim g(x) B , 有
f x A , gx B Bf x Ag x Bg x
Bf x AB AB Ag x
x1
2
Page 14
内容小结
1. 极限运算法则 Th1 Th2 Th3 Th4 Th5 Th7
(1) 函数极限法则
(2) 极限四则运算法则
注意使用条件
(3) 复合函数极限运算法则
2. 求函数极限的方法
(1) 分式函数极限求法
1) x x0 时, 用代入法 ( 分母不为 0 )
2)
x
x0
时,
对
0 0
0 (x) a u a
故
f (u) A , 因此①式成立Page. 12
定理6. 设
且 x 满足
时,
(x) a , 又 lim f (u) A, 则有 ua

2-3极限的运算法则09[1]0926


称
lim
x1
x
2
x
1 2x
3
为
0 型极限. 0
由极限定义 x→1，x≠1,
lim
x1
x
2
x
1 2x
3
lim x 1 x1( x 3)( x 1)
lim
x1
x
1
3
1. 4
约去无穷小因子法
例4
求
lim
x
2 7
x3 x3
3x2 4x2
5. 1
( 型)
分析 x 时,分子,分母的极限都是无穷大.
x x0
x x0
x x0
(2) lim [ f ( x)g( x)] lim f ( x) lim g( x) AB
x x0
x x0
x x0
(3) 若 B≠0 , 则有
lim f ( x) x x0 g( x)
lim
x x0
f (x)
A
lim g( x) B
x x0
证 (1)由 lim f ( x) A, lim g( x) B ,可知
x x0
ε 0, 1 0 及 M 0, 使得
f ( x)在某
U ( x0 )上有界
当0 x x0 1 时，有 f ( x) A
及 f (x) M
又由 lim g( x) B 知,
x x0
对于上述 > 0, 2 0,
使得当 0 x x0 2 时，有 g( x) B / 2C
n
n(n 2n2
1)
lim 1 (1 1 ) 1 . n 2 n 2
备用题
例3-1 求 lim 2 x . （0 型）

极限的性质与运算


limx3 lim1

x2
lim(x2
x2
3x 5)
23 1 3
7. 3
x2
9
2019/8/29
例2 求xl im 1x24x2x13.
解 lim (x22x3) 0, x 1
又 lim (4x1) 30,
x 1
limx22x3 0 0.
常数因子可以提到极限记号外面.
推论2 如l果 ifm i(x)存,而 在 ai为常 (i1,2 数 , ,n)则 , lim a1f1(x [)a2f2(x) anfn(x)]
lim a1f1(x)lia m 2f2(x) lia m nfn(x) 推论3 如果 lim fi(x)存(在 i1,2, ,n)则 ,
围确定。 2、此处只说有一个空心邻域，至于空心邻域有多大由
具体函数确定。
1
2019/8/29
性质3(局部保号性) 若 lim f(x)A0 ， 则 0 ， x x0
使 x U 0(x0)， f(x)0。
性质4 已 x l x i 0f 知 ( m x ) A ， 若 0 ， x 使 U 0 (x 0 ) ，
lim f1([x)f2(x) fn(x)] lim f1(x)lim f2(x)lim fn(x) 推论4 如果 lim f(x)存,在 而n是正,整 则数
lim f(x[)n ][lim f(x)n ].
推论5 如l果 im f(x)存在且 ,而 不 n是为 正,零 则 整数 lim f(x)[ ]n[lifm (x) ]n.
实际上 是我们 下一节 将要学 到的∞
消极大公因子法对分子、分母含指数形式也适用。
例 求 极l限 im (2)n 3n 。计算过程 n(2)n1 3n1

高等数学极限运算法则与性质


2.设 f(x)Q P((x x)),且 Q (x0)0, 则有
limP(x)
limf(x) xx0
xx0
limQ(x)
xx0
P(x0) Q ( x0 )
f(x0).
若Q(x0)0, 则商的法则不 . 能应用
5
首页
上页
返回
下页
结束
铃
例2 求lxim 1x2x22x13.
解 x1时,分子 ,分母的极限. 都 ( 0是 型 )零 0
2
首页
上页
返回
下页
结束
铃
推论1 如l果 im f(x)存,在 而 c为常 ,则 数 lim cf([x)]clim f(x).
常数因子可以提到极限记号外面.
推论2 如果 lim f(x)存,在 而 n是正整 ,则数 limf([x)n ][lim f(x)n ].
3
首页
上页
返回
下页
结束
铃
二、求极限方法举例
例1 求lx im 2x2x33x15.
解 li(m x23x5)lim x2li3 m xli5 m
x 2
x 2
x 2
x 2
(lix m )23lix m li5 m
x 2
x 2 x 2
2232530,
lxim 2 x2x33x15
lim(
x2
lim(x2
x3 1) 3x
5)
23 1 3
7 3
先用 x3去除分子,再 分求 母极 . 限
35
lx im 27xx33
3x2 4x2
5lim2xx3
1
x 4 1 7xx3
2 7
.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
ln li[(m 1x)x]lne1. x 0
例2 求limex 1. x0 x
解 令 ex1y, 则 xln 1 (y),
当 x 0 时 ,y 0 .
原式 lim y y0ln1(y)
lim 1
y0
ln(1
1
y) y
1.
同理可得
ax 1 lim lna.
x0 x
例如, limsinx 1 x0 x
y sin x x
limnsin11,
n
n
limnsin1 1,
n
n
ln i m nn21sin nn211
函数极限与数列极限的关系
函数极限存在的充要条件是它的任何子列的极 限都存在,且相等.
dhanyavaad
达尼阿瓦德
limx[1]1 x0 x
(二)极限的运算法则
性质2.9
设limf(x) A,limg(x) B,则
xX
xX
(1) lim[f(x) g(x)] limf(x) limg(x) AB;
xX
xX
xX
(2) limcf(x) climf(x)
xX
xX
(3) lim[f(x)g(x)] limf(x) limg(x) AB;
消除0因子
(5) lim( 1x x) 根式有理化 x
(6) lx i1m (1 1x1 3x2) 先通分
(7) limx8 x643 x4
1
变量替 :x6换 t
性质2.10(复合函数的极限法则)
若 lig m (x )A (或 )y ,g (x )A ,lifm (y)B ,
x X
y A
则 lifm (g (x ) )lifm (y)B
x X
y A
性2.质 1中 0 条 g(x) 件 A ,不能 ,否 省则 去结论 .
意义 1.极限符号可以与函数符号互换; 2.变量(u 代 (换 x)的 ) 理论 . 依据
例1 求lim ln1(x).
x0
x
1
解 原 l式 ilm n 1x ()x x 0
xX
xX
xX
(4)
limf
(x)
Байду номын сангаас
limf
xX
(x)
A,
其中B 0.
xXg(x) limg(x) B
xX
结:论 如l果 im f(x)存,在 而 n是正,则 整数 x X
lim [f(x)n ][lim f(x)n ].
x X
x X
例1 求下列极限
(1)lx i2m x2x33x15.
解 li(m x23x5)lix m 2li3 m xli5 m
例1 求lx im 0x1x
解:1 x11 x1 x ( 如 : 2 . 5 2 , 2 . 5 1 2 . 5 2 . 5 , )
当 x 0 ,有 1 x x 1 x 1 x l 0 i x [ m 1 x ] 1 当 x 0 ,有 1 x 1 x 1 x x l 0 i x [ m 1 x ] 1
x 2
x 2
x 2
x 2
(lix m )23 lix m li5 m
x 2
x 2 x 2
2 232530,
lx im 2x2x33x15lilxmi(m2xx233lxxim 215)
23 1 3
7 3
.
x2
(2) limxex x2
(3)
lxim 82xx22
6x 3 4x 7
(4) limxn 1 x1 x1