最新1.4极限的性质与四则运算法则

函数极限的四则运算法则函数极限是数学中重要的概念之一，它在数学分析和微积分中有着广泛的应用。

四则运算法则指的是对函数进行加减乘除运算时，其极限的运算规则。

在本文中，我们将对四则运算法则进行详细的说明。

1.加法法则：如果有两个函数 f(x) 和 g(x)，且它们的极限都存在，则它们的和的极限等于两个极限的和，即lim(x→a) [f(x) + g(x)] = lim(x→a)f(x) + lim(x→a) g(x)。

证明如下：假设lim(x→a) f(x) = L1，lim(x→a) g(x) = L2，我们需要证明lim(x→a) [f(x) + g(x)] = L = L1 + L2根据极限的定义，我们可以找到两个足够小的正数ε1和ε2，使得当0<，x-a，<δ1时，有，f(x)-L1，<ε1，当0<，x-a，<δ2时，有，g(x)-L2，<ε2取δ = min{δ1, δ2}，则当 0 < ，x-a，< δ 时，有，f(x) - L1，< ε1 且，g(x) - L2，< ε2此时，我们可以将不等式，f(x)-L1，+，g(x)-L2，<ε1+ε2转化为不等式，f(x)+g(x)-(L1+L2)，<ε1+ε2根据极限的定义，当，f(x) + g(x) - (L1 + L2)，< ε1 + ε2 时，有，x - a，< δ，即证明了lim(x→a) [f(x) + g(x)] = L1 +L22.减法法则：如果有两个函数 f(x) 和 g(x)，且它们的极限都存在，则它们的差的极限等于两个极限的差，即lim(x→a) [f(x) - g(x)] = lim(x→a) f(x) - lim(x→a) g(x)。

证明方法与加法法则类似，略。

3.乘法法则：如果有两个函数 f(x) 和 g(x)，且它们的极限都存在，则它们的乘积的极限等于两个极限的乘积，即lim(x→a) [f(x) * g(x)] =lim(x→a) f(x) * lim(x→a) g(x)。

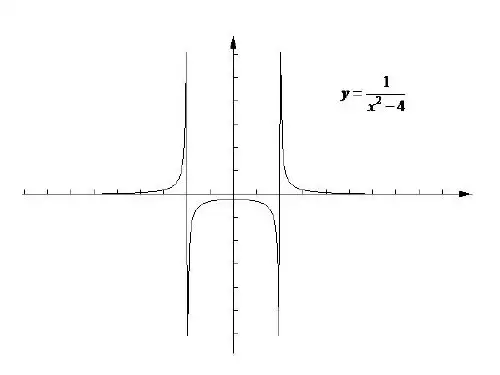
1.4极限运算的法则定理1.11（极限的四则运算法则）若()()0lim ,lim x x x xf x ag x b →→==，则 （ⅰ）()()()()0lim lim lim x x x x x x f x g x f x g x a b →→→±=±=+⎡⎤⎣⎦；（ⅱ）()()()()0lim lim lim x x x x x x f x g x f x g x ab →→→=⋅=⎡⎤⎣⎦；（ⅲ）()()()()()000lim lim0.lim x x x x x x f x f x a b g x g x b→→→==≠ 证 只证（ⅰ）、（ⅱ）.（ⅰ）0,ε∀>因()0lim x x f x a →=，故对正数2ε，存在相应的正数1δ使得，当010x x δ<-<时，有().2f x a ε-< （1）因()0lim x x g x b →=，则对正数2ε，存在相应的正数2δ使得，当020x x δ<-<时，有 ().2g x b ε-< （2）取{}12min ,δδδ=，则当00x x δ<-<时，有()()()()().22f xg x a b f x a g x bεεε±-±≤-+-⎡⎤⎣⎦<+=故()()()()0lim lim lim x x x x x x f x g x a b f x g x →→→±=+=±⎡⎤⎣⎦.（ⅱ）因()0lim x x f x a →=,故()f x 在点0x 的某邻域内有界,即存在正数1δ使得,当010x x δ<-<时,有()1f x M ≤这里,1M 是一个正常数.取正数{}1max ,M M b=,则当1,.M M b M ≤≤于是，当010x x δ<-<时，有().f x M ≤ （3）0,ε∀>因()0lim x x f x a →=,故相应于正数2Mε,存在正数2δ使得,当020x x δ<-<时,有().2f x a Mε-<(4)又因()0lim x x g x b →=,故相应于正数2Mε,存在正数3δ使得,当030x x δ<-<时,有 ().2g x b Mε-< (5)取正数{}123min ,,,δδδδ=则当00x x δ<-<时,（3），（4），（5）两式都成立，此时，有()()()()()()()()()()()()().22f x g x ab f x g x f x b f x b ab f x g x f x b f x b ab f x g x b f x b b M M MMεεε-=-+-≤-+-=-+-=⋅+⋅=故()()()()0lim lim lim .x x x x x x f x g x ab f x g x →→→==⋅⎡⎤⎣⎦例1—4—1 求()1lim 21.x x →-解()()1111lim 21lim 2lim12lim 1211 1.x x x x x x x →→→→-=-=-=⋅-= 例1—4—2求3222234lim .53x x x x x x →-+--+ 解()()323222222lim 2342342lim.533lim 53x x x x x x x x x x x x x →→→-+--+-==--+-+例1—4—3 求233lim.9x x x →-- 解()()()323333lim13311limlim lim .9333lim 36x x x x x x x x x x x x →→→→→--====--+++ 例1—4—4 求3113lim .11x x x →⎛⎫- ⎪++⎝⎭解()()()()()()3211122111213lim lim 1111lim 22lim1.1lim 1x x x x x x x x x x x x x x x x x x →→→→→+-⎛⎫-= ⎪+++-+⎝⎭--===--+-+例1—4—5 求3232342lim.753x x x x x →∞-++- 解323332334242lim 333423lim lim .535375377lim 7x x x x x x x x x x x x x x x x →∞→∞→∞→∞⎛⎫-+-+ ⎪-+⎝⎭===+-⎛⎫+-+- ⎪⎝⎭例1—4—6 （略）例1—4—7 求lim, 1.1nn n a a a →∞≠+ 解 若1a <，则lim 0.n n a →∞= ()lim lim0.1lim 1n nn nn n n a aa a →∞→∞→∞==++当1a >，111,lim 0.n an →∞<=lim11lim lim 1.1111lim 1nx nn nn x x a a a a →∞→∞→∞→∞===+⎡⎤⎛⎫⎛⎫++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦作业 p37 1.（1），（3），（5）.习题1—41. 计算下列极限（1）245lim 3x x x →+-；解()()22224444444lim 5lim lim5545lim 21.3lim 3lim lim343x x x x x x x x x x x x x →→→→→→→++++====---- （3）22356lim 815x x x x x →-+-+；解()()()()22333235621lim lim lim .8153552x x x x x x x x x x x x x →→→---+-===--+--- （5）()22limh x h x h→+-；解()()222002limlim lim 22.h h h x h x xh h x h x hh→→→+-+==+= （7）221lim 21x x x x →∞---；解22221111limlim .112122x x x x x x x x→∞→∞--==----（9）3113lim 11x x x →⎛⎫- ⎪--⎝⎭； 解()()()()()()232112211132lim lim 11111221limlim .1311x x x x x x x x x x x x x x x x x x x →→→→+-⎛⎫-= ⎪---++⎝⎭---==-=++-++（11）()()525115lim x x x x x →+-++;解()()52345252502330115151010515lim lim10105lim 10.1x x x x x x x x x x xx x x x x x x x →→→+-++++++--=+++++=+（13）()2121limn n n →∞+++-；解()()2211211112lim lim lim 1.22n n n n n n n n n →∞→∞→∞-+++-⎛⎫==-= ⎪⎝⎭。