同步卫星及变轨问题

卫星变轨问题知识点总结
卫星变轨是指卫星在轨道上偏离原有轨道进行调整的过程，用于满足不同的需求，如太阳同步轨道、地球静止轨道等。

以下是卫星变轨问题的几个知识点总结：
1. 变轨方式：变轨主要有化学推进剂变轨和电推进剂变轨两种方式。

前者通常采用火箭发动机进行推进，后者则利用电磁力进行推进。

2. 变轨方法：变轨方法通常包括单次变轨、多次变轨、连续变轨等几种。

其中单次变轨是指通过一次加速或减速达到目标轨道；多次变轨是分数次进行变轨，实现最终目标轨道；连续变轨则是通过对卫星进行定期推进来维持轨道的稳定。

3. 变轨技术：变轨技术主要包括贴近飞行、引力助推、轨道选择等。

贴近飞行需要精确掌握卫星的运动状态，以便在飞行过程中进行微调；引力助推则是利用行星或月球等天体的引力来实现变轨；轨道选择则是根据具体任务需求选择不同的轨道。

4. 变轨误差：变轨过程中存在着各种误差，如发动机性能波动、气象条件变化等。

这些误差会影响卫星的运行轨迹，需要对其进行修正和控制。

5. 动力学方程：卫星的运动状态可以通过动力学方程描述。

动力学方程包括万有引力、空气阻力、电磁效应等多个因素，并可通过数值积分方法求解得到卫星的运动状态。

总之，卫星变轨是卫星运行中重要的环节之一，需要精确掌握
变轨技术和动力学方程，保证卫星能够按照预定轨道稳定运行，实现各种任务目标。

第八讲：卫星变轨问题和双星问题一、卫星相遇问题两颗卫星在同一轨道平面内同向绕地球做匀速圆周运动，a 卫星的角速度为ωa ，b 卫星的角速度为ωb .若某时刻两卫星正好同时通过地面同一点正上方，相距最近，如图甲所示．当它们转过的角度之差Δθ＝π，即满足ωa Δt －ωb Δt ＝π时，两卫星第一次相距最远，如图乙所示．当它们转过的角度之差Δθ＝2π，即满足ωa Δt －ωb Δt ＝2π时，两卫星再次相距最近．二、卫星变轨问题1．变轨分析(1)卫星在圆轨道上稳定运行时， G Mmr 2＝m v 2r＝mω2r ＝m ⎝⎛⎭⎫2πT 2r . (2)当卫星的速度突然增大时，G Mm r 2<m v 2r ，即万有引力不足以提供向心力，卫星将做离心运动，脱离原来的圆轨道，轨道半径变大．当卫星进入新的轨道稳定运行时，由v ＝GMr可知其运行速度比原轨道时减小，但重力势能、机械能均增加．(3)当卫星的速度突然减小时，G Mm r 2>m v 2r ，即万有引力大于所需要的向心力，卫星将做近心运动，脱离原来的圆轨道，例题、如图所示，北斗导航系统中的两颗工作卫星均绕地心做匀速周运动，且轨道半径为r ，某时刻工作卫星1、2分别位于轨道上的A 、B 两个位置，若两卫星均沿顺时针方向运行，地球表面的重力加速度为g ，地球半径为R ，不计卫星间的相互作用力。

下列判断正确的是（ ）例题、如图所示，三个质点a 、b 、c 质量分别为m 1、m 2、M ，（M ＞＞m 1，M ＞＞m 2）．a 、b 在同一平面内绕c 沿逆时针方向做匀速圆周运动，它们的周期之比T a ：T b ＝1：k ．（k ＞1，为正整数）从图示位置开始，在b 运动一周的过程中，则（ ）A ．a 、b 距离最近的次数为k 次B ．a 、b 距离最近的次数为k+1次C ．a 、b 、c 共线的次数为2k 次轨道半径变小．当卫星进入新的轨道稳定运行时，由v ＝GMr可知其运行速度比原轨道时增大，但重力势能、机械能均减小．2．三个运行物理量的大小比较(1)速度：设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v 1、v 3，在轨道Ⅱ上过A 点和B 点速率分别为v A 、v B .在A 点加速，则v A >v 1，在B 点加速，则v 3>v B ，又因v 1>v 3，故有v A >v 1>v 3>v B .(2)加速度：因为在A 点，卫星只受到万有引力作用，故不论从轨道Ⅰ还是轨道Ⅱ上经过A 点，卫星的加速度都相同，同理，经过B 点加速度也相同．(3)周期：设卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行周期分别为T 1、T 2、T 3，轨道半径分别为r 1、r 2(半长轴)、r 3，由开普勒第三定律r 3T2＝k 可知T 1<T 2<T 3. 三、多星模型1．定义绕公共圆心转动的两个星体组成的系统，我们称之为双星系统．如图所示．A ．这两颗卫星的加速度大小相等，均为22gR rB ．卫星1出A 位置运动到B 位置所需的时间是3rr R gC ．这两颗卫星的机械能一定相等D ．卫星1向后喷气就一定能够追上卫星22．特点(1)各自所需的向心力由彼此间的万有引力提供，即 Gm 1m 2L2＝m 1ω21r 1， Gm 1m 2L 2＝m 2ω22r 2. (2)两颗星的周期及角速度都相同，即T 1＝T 2，ω1＝ω2. (3)两颗星的半径与它们之间的距离关系为：r 1＋r 2＝L .3．两颗星到圆心的距离r 1、r 2与星体质量成反比，即m 1m 2＝r 2r 1.针对训练题型1：相遇问题1．如图所示，A 和B 两行星绕同一恒星C 做圆周运动，旋转方向相同，A 行星的周期为T 1，B 行星的周期为T 2，某一时刻两行星相距最近，则（ ）A ．经过T 1+T 2两行星再次相距最近B ．经过两行星再次相距最近C ．经过两行星相距最远D ．经过两行星相距最远2．已知地球自转周期为T0，有一颗与同步卫星在同一轨道平面的低轨道卫星，自西向东绕地球运行，其运行半径为同步轨道半径的四分之一，该卫星至少相隔多长时间才在同一城市的正上方出现一次．（）A．B．C．D．题型2：变轨问题3．如图所示，假设月球半径为R，月球表面的重力加速度为g0，飞船在距月球表面高度为3R的圆形轨道Ⅰ上运动，到达轨道的A点点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动。

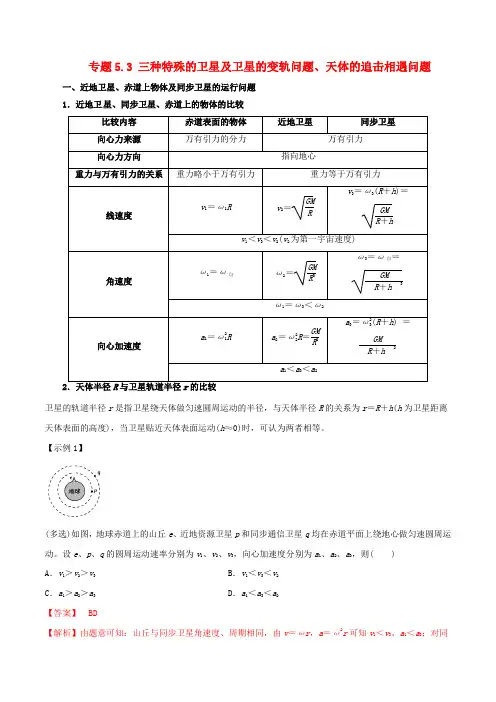
专题5.3 三种特殊的卫星及卫星的变轨问题、天体的追击相遇问题一、近地卫星、赤道上物体及同步卫星的运行问题1．近地卫星、同步卫星、赤道上的物体的比较比较内容赤道表面的物体近地卫星同步卫星向心力来源万有引力的分力万有引力向心力方向指向地心重力与万有引力的关系重力略小于万有引力重力等于万有引力线速度v1＝ω1R v2＝GMRv3＝ω3(R＋h)＝GMR＋hv1＜v3＜v2(v2为第一宇宙速度)角速度ω1＝ω自ω2＝GMR3ω3＝ω自＝GMR＋h3ω1＝ω3＜ω2向心加速度a1＝ω21R a2＝ω22R＝GMR2a3＝ω23(R＋h) ＝GMR＋h2a1＜a3＜a2卫星的轨道半径r是指卫星绕天体做匀速圆周运动的半径，与天体半径R的关系为r＝R＋h(h为卫星距离天体表面的高度)，当卫星贴近天体表面运动(h≈0)时，可认为两者相等。

【示例1】(多选)如图，地球赤道上的山丘e、近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动。

设e、p、q的圆周运动速率分别为v1、v2、v3，向心加速度分别为a1、a2、a3，则( )A．v1＞v2＞v3B．v1＜v3＜v2C．a1＞a2＞a3D．a1＜a3＜a2【答案】BD【解析】由题意可知：山丘与同步卫星角速度、周期相同，由v＝ωr，a＝ω2r可知v1＜v3、a1＜a3；对同步卫星和近地资源卫星来说，满足v ＝GM r 、a ＝GMr2，可知v 3＜v 2、a 3＜a 2。

故选项B 、D 正确。

【示例2】(多选)同步卫星离地心距离为r ，运行速率为v 1，加速度为a 1，地球赤道上的物体随地球自转的向心加速度为a 2，第一宇宙速度为v 2，地球的半径为R ，则下列比值正确的是( )A.a 1a 2＝rRB.a 1a 2＝r 2R2 C.v 1v 2＝r R D.v 1v 2＝R r【答案】： AD【示例3】(2016·四川理综·3)国务院批复，自20XX 年起将4月24日设立为“中国航天日”.1970年4月24日我国首次成功发射的人造卫星东方红一号，目前仍然在椭圆轨道上运行，其轨道近地点高度约为440 km ，远地点高度约为2 060 km ；1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km 的地球同步轨道上.设东方红一号在远地点的加速度为a 1，东方红二号的加速度为a 2，固定在地球赤道上的物体随地球自转的加速度为a 3，则a 1、a 2、a 3的大小关系为( ) A.a 2＞a 1＞a 3 B.a 3＞a 2＞a 1 C.a 3＞a 1＞a 2 D.a 1＞a 2＞a 3【答案】 D【解析】 由于东方红二号卫星是同步卫星，则其角速度和赤道上的物体角速度相等，根据a ＝ω2r ，r 2>r 3，则a 2>a 3；由万有引力定律和牛顿第二定律得，G Mmr2＝ma ，由题目中数据可以得出，r 1<r 2，则a 2<a 1；综合以上分析有，a 1>a 2>a 3，选项D 正确.【示例4】．有a 、b 、c 、d 四颗地球卫星，a 在地球赤道上未发射，b 在地面附近近地轨道上正常运动，c 是地球同步卫星，d 是高空探测卫星，各卫星排列位置如图，则有( )A ．a 的向心力由重力提供B ．c 在4 h 内转过的圆心角是π6C ．b 在相同时间内转过的弧长最长D ．d 的运动周期有可能是20 h 【答案】 C二、 卫星的变轨问题 1．三种情境2．变轨问题的三点注意(1)航天器变轨时半径的变化，根据万有引力和所需向心力的大小关系判断；稳定在新轨道上的运行速度变化由v ＝GMr判断。

专题强化训练二：卫星（近地、同步、极地）的宇宙航行运动规律与变轨问题技巧归纳：人造卫星的变轨问题1.变轨问题概述 (1)稳定运行卫星绕天体稳定运行时，万有引力提供了卫星做圆周运动的向心力，即G Mmr 2＝m v 2r .(2)变轨运行卫星变轨时，先是线速度大小v 发生变化导致需要的向心力发生变化，进而使轨道半径r 发生变化.①当卫星减速时，卫星所需的向心力F 向＝m v 2r 减小，万有引力大于所需的向心力，卫星将做近心运动，向低轨道变轨.②当卫星加速时，卫星所需的向心力F 向＝m v 2r 增大，万有引力不足以提供卫星所需的向心力，卫星将做离心运动，向高轨道变轨. 2.实例分析 (1)飞船对接问题①低轨道飞船与高轨道空间站对接时，让飞船合理地加速，使飞船沿椭圆轨道做离心运动，追上高轨道空间站完成对接(如图甲所示).②若飞船和空间站在同一轨道上，飞船加速时无法追上空间站，因为飞船加速时，将做离心运动，从而离开这个轨道.通常先使后面的飞船减速降低高度，再加速提升高度，通过适当控制，使飞船追上空间站时恰好具有相同的速度，如图乙所示.(2)卫星的发射、变轨问题如图发射卫星时，先将卫星发射至近地圆轨道1，在Q 点点火加速做离心运动进入椭圆轨道2，在P 点点火加速，使其满足GMmr 2＝m v 2r，进入圆轨道3做圆周运动.一、单选题1．（2022·江苏省江都中学高三开学考试）据报道，一颗来自太阳系外的彗星擦火星而过。

如图所示，设火星绕太阳在圆轨道上运动，运动半径为r ，周期为T 。

该彗星在穿过太阳系时由于受到太阳的引力，轨道发生弯曲，彗星与火星在圆轨道的A 点“擦肩而过”。

已知万有引力常量G ，则（ ）A．可计算出火星的质量B．可计算出彗星经过A点时受到的引力C．可确定太阳分别对彗星和火星的引力在A点产生的加速度相等D．可确定彗星在A点的速度大小为2r vTπ=2．（2022·云南·昆明一中模拟预测）随着“嫦娥奔月”梦想的实现，我国不断刷新深空探测的“中国高度”。

r 3 GM专题八、卫星变轨问题问题分析卫星环绕地球做匀速圆周运动时所需向心力由地球对它的万有引力提供，稳定运行时，其线速度、角速度、周期、向心加速度均为定值，且仅与轨道半径有关而与卫星质量无关；如果卫星所受万有引力不刚好提供向心力， 其运行速率及轨道半径均要发生变化，即发生变轨运动：若使卫星速率减小，则万有引力大于所需向心力，轨道半径将减小；若使卫星速率增大，则万有引力小于所需向心力，轨道半径将增大。

Mmv 224 2Gr2=m=mω r = mrT 2r =ma 向=mg ，解得 v =， ω= ，a =g = GM ，T =2π， 向r 2由于卫星的线速度决定着卫星的动能，即 E k = 1 2mv 2， 而卫星高度越高，其具有的重力势能也就越大，对于上述 规律可以简记为：高轨低速小动能，高轨高势大周期.具体含义是卫星的运行轨道越高，卫星的线速度、角速度、向心加速度、卫星所在位 置处的重力加速度，就越小；卫星的动能越小，卫星的重力势能就越大，卫星运行周 期也越大，反之则反.李老师温馨提示：在遇到卫星轨道转移问题时，椭圆轨道和圆周轨道的相切点的线速度时，要牢记内小外大，其含义是，内轨道的线速度小，外轨道的线速度大!如图所示，M 点是轨道 2 和 3 的相切点，2 是内轨道，3 是外轨道，则有 v 2<v 3， 原因是对于卫星沿轨道 3 圆周运动通过 M 点时，满足 GMm v 2=m 2 ，而轨道 2 由远地点 M 点向近地点 N 点运动r 2r时做近心运动，满足 GMm v 2>m 2 ；卫星沿轨道 1 圆周运动通过 N 点，满足 G r 2rMm v 2=m 1 r2 r，而轨道 2 由远地点 N点向近地点 M 点运动时做离心运动，满足 GMm r 2 v 2 <m 2 ，则有 v 1<v 2。

r这个规律同样适合于玻尔理论，氢原子能级问题！卫星变轨的实质两类变轨 离心运动 近心运动 变轨起因 卫星速度突然增大卫星速度突然减小万有引力与向心力 的大小关系GMm <mv 2r2rGMm >mv 2r2r变轨结果转变为椭圆轨道运动或在较大半径 圆轨道上运动转变为椭圆轨道运动或在较小半径圆 轨道上运动GM rGM r 33 2 MN1在处理下列实际问题中，请你先用上述 14 个文字进行判断，可以做到秒杀答案，然后再详细参考一下解析！【调研 1】(2013·新课标全国Ⅰ)2012 年 6 月 18 日，“神州九号”飞船与“天宫一号”目标飞行器在离地面343km 的近圆形轨道上成功进行了我国首次载人空间交会对接．对接轨道所处的空间存在极其稀薄的大气， 下面说法正确的是 ()A ．为实现对接，两者运行速度的大小都应介于第一宇宙速度和第二宇宙速度之间B ．如不加干预，在运行一段时间后，“天宫一号”的动能可能会增加C. 如不加干预，“天宫一号”的轨道高度将缓慢降低D. 航天员在“天宫一号”中处于失重状态，说明航天员不受地球引力作用【解析】第一宇宙速度为最大环绕速度，天宫一号的线速度一定小于第一宇宙速度，故 A 选项错误；根据万有引力提供向心力，有 G Mm=m v r 2 r，解得v ，得轨道高度降低，卫星的线速度增大，故动能将增大，所以 B 选项正确；卫星由于摩擦阻力做功，利用控制变量，假设轨道高度不变，只能是速度减小，提供的引力大于卫星所需要的向心力，故卫星将做近心运动，即轨道半径将减小，故 C 项正确；航天员在“天宫一号”中处于失重状态，而这恰好是航天员受地球引力全部用于做圆周运动的向心力导致的完全失重状态，D 选项错误． 答案 BC【调研2】2008 年9 月25 日至28 日我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱．飞船先沿椭圆轨道飞行，后在远地点 343 千米处点火加速，由椭圆轨道变成高度为 343 千米的圆轨道，在此圆轨道上飞船运行周期约为 90 分钟．下列判断正确的是 ( )A. 飞船变轨前后的机械能相等B. 飞船在圆轨道上时航天员出舱前后都处于失重状态C. 飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度D. 飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度【解析】飞船点火变轨，前后的机械能不守恒，所以 A 项不正确．飞船在圆轨道上时万有引力来提供向心力，航天员出舱前后都处于失重状态，B 项正确．飞船在此圆轨道上运动的周期 90 分钟小于同步卫星运动 的周期 24 小时，根据 T =2π，可知，飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度，C 项正ω确．飞船变轨前通过椭圆轨道远地点时只有万有引力来提供加速度，变轨后沿圆轨道运动也是只有万有引力来提供加速度，所以相等，D 项不正确． 答案 BC【调研 3】探测器绕月球做匀速圆周运动，变轨后在周期较小的轨道上仍做匀速圆周运动，则变轨后与2变轨前相比( )GM rGM r A ．轨道半径变小 B ．向心加速度变小 C ．线速度变小D ．角速度变小【解析】 由开普勒定律知，对绕同一中心天体的所有卫星，轨道的半长轴的三次方跟公转周期的二次方的R 32π比值都相等，即 T 2 =k ，知周期减小，则半径减小，A 选项正确；由ω= T，知角速度增大，D 选项错误；根据 G Mm =ma ，得 a = GM r 2 r 2 ，半径减小，向心加速度变大，B 选项错误；由 G Mm r 2 v 2 =m ，解得线速度 v = ， r得轨道高度降低，卫星的线速度增大，C 选项错误． 答案 A【调研 4】“神舟十号”与“天宫一号”已 5 次成功实现交会对接。