点 线 面 体拓展练习

2019年最新巩固数学七年级训练《点、线、面、体》尽快地掌握科学知识，迅速提高学习能力,由查字典数学网为您提供的2019年最新巩固数学七年级训练《点、线、面、体》，希望给您带来启发!观察内容的选择，我本着先静后动，由近及远的原则，有目的、有计划的先安排与幼儿生活接近的，能理解的观察内容。

随机观察也是不可少的，是相当有趣的，如蜻蜓、蚯蚓、毛毛虫等，孩子一边观察，一边提问，兴趣很浓。

我提供的观察对象，注意形象逼真，色彩鲜明，大小适中，引导幼儿多角度多层面地进行观察，保证每个幼儿看得到，看得清。

看得清才能说得正确。

在观察过程中指导。

我注意帮助幼儿学习正确的观察方法，即按顺序观察和抓住事物的不同特征重点观察，观察与说话相结合，在观察中积累词汇，理解词汇，如一次我抓住时机，引导幼儿观察雷雨，雷雨前天空急剧变化，乌云密布，我问幼儿乌云是什么样子的，有的孩子说：乌云像大海的波浪。

有的孩子说“乌云跑得飞快。

”我加以肯定说“这是乌云滚滚。

”当幼儿看到闪电时，我告诉他“这叫电光闪闪。

”接着幼儿听到雷声惊叫起来，我抓住时机说：“这就是雷声隆隆。

”一会儿下起了大雨，我问：“雨下得怎样?”幼儿说大极了，我就舀一盆水往下一倒，作比较观察，让幼儿掌握“倾盆大雨”这个词。

雨后，我又带幼儿观察晴朗的天空，朗诵自编的一首儿歌：“蓝天高，白云飘，鸟儿飞，树儿摇，太阳公公咪咪笑。

”这样抓住特征见景生情，幼儿不仅印象深刻，对雷雨前后气象变化的词语学得快，记得牢，而且会应用。

我还在观察的基础上，引导幼儿联想，让他们与以往学的词语、生活经验联系起来，在发展想象力中发展语言。

如啄木鸟的嘴是长长的，尖尖的，硬硬的，像医生用的手术刀―样，给大树开刀治病。

通过联想，幼儿能够生动形象地描述观察对象。

1.圆锥可以看作是由一个_______旋转得到的( ) A.矩形(长方形) B.等腰梯形C.半圆D.直角三角形思路解析：拿一个三角板旋转，不难得出答案? 答案:D 2.包围着几何体的是_______，面与面相交形成______，线与线相交形成_______. 答案:面线点3.数一数长方体、四面体的面数、棱数和顶点数，并填下表：名称面数(f) 顶点数(v) 棱数(e) 长方形四面体思路解析：利用实物我们不难得到长方体、四面体的面数、棱数和顶点数. 答案: 名称面数(f) 顶点数(v) 棱数(e) 长方体6 8 12 四面体4 4 6 10分钟训练(巩固类训练，可用于课后) 1.五棱柱的面有( ) A.5个B.6个C.7个D.8个思路解析：棱柱有两个底面，关键数清有几个侧面? 答案:C 2.图4-1-11的图形中绕直线l旋转一周，能得到右边立体图形的是( ) 图4-1-11 思路解析：圆锥的锥尖是由角旋转得到的，两个锥尖的几何体是由三角形旋转得到的? 答案:D 3.______棱锥又叫四面体，它的各个面都是______形;它有______条棱，有______个顶点. 思路解析：棱锥当中，只有三棱锥有四个面? 答案:三三角6 4 4.飞机飞行表演在空中留下漂亮的彩带，用数学知识解释为_______. 思路解析：飞机可以看作一个点，点运动形成线. 答案:点动成线5.将图4-1-12中的图形按要求分类：(1)若按柱、锥、球划分;(2)若按组成面的曲或平划分. 图4-1-12 思路解析：分类时一定要注意把握好特征，做到不重不漏，标准统一. 答案:(1)柱体：①，③，④，⑤，⑦;锥体：②;球体：⑥?与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。

4.1.2 点、线、面、体分层作业1．（2021秋•伊川县期末）“枪挑一条线，棍扫一大片”，从数学的角度解释为（）A．点动成线，线动成面B．线动成面，面动成体C．点动成线，面动成体D．点动成面，面动成线【解析】解：“枪挑一条线，棍扫一大片”，从数学的角度解释为：点动成线，线动成面，故选：A．2．（2022秋•青岛期中）下列平面图形绕虚线旋转一周，能形成如图所示几何体的是（）A．B．C．D．【解析】解：将平面图形绕着虚线旋转一周可以得到的几何体为，故选：C．3．（2022秋•雁塔区校级期中）下列几何体中可以由平面图形绕某条直线旋转一周得到的是（）A．B．C ．D ．【解析】解：因为平面图形绕某条直线旋转一周得到的几何体必须有曲面，所以B 选项符合题意，故选：B ．4．（2022春•绥棱县期末）长方形长5厘米，宽3厘米，以宽为轴旋转一周得到圆柱的体积是（ ）立方厘米．A ．225.5B ．235.5C ．245.5D ．255.5【解析】解：由题意可知，圆柱体的底面半径为5厘米，高为3厘米，所以体积为25375235.5ππ⨯⨯=≈（立方厘米），故选：B ．5．（2022秋•朝阳区校级期中）用纸片和小棒做成下面的小旗，快速旋转小棒，所形成的图形正确顺序是（ ）A ．①②③④B ．③④①②C ．①③②④D ．④②①③【解析】解：因为半圆绕直径旋转可形成球体，长方形绕一边旋转可形成圆柱体，三角形绕一直角边旋转可形成圆锥，直角梯形绕下底旋转可形成圆柱与圆锥的组合体．所以旋转小棒，所形成的图形正确顺序是③④①②．故选：B ．6．（2022秋•单县校级月考）笔尖在纸上快速滑动写出了一个又一个字，这说明了 ；直角三角形绕它的直角边旋转一周，形成了一圆锥体，这说明了 ．“齐天大圣”孙悟空有一个宝贝——金箍棒，当他快速旋转金箍棒时，展现在我们眼前的是一个圆的形象，这说明 ．【解析】解：“笔尖”可近似看作“点”笔尖在纸上快速滑动，说明点动成线，直角三角形可以看作是“面”，旋转一周形成了一圆锥体，说明“面动成体”，“金箍棒”可近似看作“线段”，快速旋转金箍棒，展现在我们眼前的是一个圆的形象，实际上就是“线动成面”，故答案为：点动成线，面动成体，线动成面．7．（2022秋•奎文区期中）如图，下面的几何体是由图（填写序号）的平面图形绕直线l旋转一周得到的．【解析】解：由图可知，只有图②绕直线l旋转一周得到如图所示立体图形．故答案为：②．8．（2022秋•子洲县校级月考）如图，某银行大堂的旋转门内部由三块宽为2m、高为3m的玻璃隔板组成．（1）将此旋转门旋转一周，能形成的几何体是，这能说明的事实是（选择正确的一项填入）．A．点动成线B．线动成面C．面动成体（2）求该旋转门旋转一周形成的几何体的体积．（边框及衔接处忽略不计，结果保留)【解析】解：（1）因为旋转门的形状是长方形，所以旋转门旋转一周，能形成的几何体是圆柱，这能说明的事实是面动成体．故答案为：圆柱，C ．（2）该旋转门旋转一周形成的几何体是圆柱，体积为：232312()m ππ⨯⨯=．故形成的几何体的体积是312m π．9．（2021秋•建宁县期中）已知如图是边长为2cm 的小正方形，现小正方形绕其对称轴线旋转一周，可以得到一个几何体，求所得的这个几何体的体积．【解析】解：小正方形绕着对称轴所在的直线旋转一周，所得到的圆柱体的底面半径为1cm ，高为2cm ，所以体积为23122()cm ππ⨯⨯=，答：这个几何体的体积为2π3cm ．10．（2022秋•朝阳区校级期中）绕一个直角三角形（如图）的长直角边旋转一周，得到一个立体图形．（1）这个立体图形是什么？（2）这个立体图形的体积是多少？（单位：厘米， 3.14)π≈【解析】解：（1）绕一个直角三角形（如图）的长直角边旋转一周，得到一个圆锥；答：这个立体图形是圆锥；（2）21 3.14343⨯⨯⨯13.1494=⨯⨯⨯3=（立方厘米），37.68答：这个立体图形的体积是37.68立方厘米．11．（2022秋•迎泽区校级月考）下列四个选项绕直线旋转一周可以得到如图立体图形的是（）A．B．C．D．【解析】解：由长方形绕着它的一边所在直线旋转一周可得到圆柱体，如图立体图形是两个圆柱的组合体，则需要两个一边对齐的长方形，绕对齐边所在直线旋转一周即可得到．故选：A．12．（2021秋•玄武区期末）将如图所示的长方形绕它的对角线所在直线旋转一周，形成的几何体是（）A．B．C．D．【解析】解：一个长方形绕它的对角线所在直线旋转一周，得到的几何体是如下：故选：B．13．（2021秋•宣汉县期末）在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝，密密麻麻地斜织着”的语句，这里把雨看成了线，这说明了（）A ．点动成线B ．线动成面C ．面动成体D ．以上都不对【解析】解：在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝，密密麻麻地斜织着”的语句，这里把雨看成了线，这说明了：点动成线，故选：A ．14．（2022秋•市中区校级月考）你见过一种折叠灯笼吗？它看起来是平面的，可是提起来后却变成了美丽的灯笼，这个过程可近似地用哪个数学原理来解释（ ）A ．点动成线B ．线动成面C ．面动成体D ．面与面相交的地方是线【解析】解：由平面图形变成立体图形的过程是面动成体，故选：C ．15．（2022秋•尤溪县期中）现有一个长方形，长和宽分别为3cm 和2cm ，绕它的一条边所在的直线旋转一周，得到的几何体的体积为（ ）A ．12πB ．27πC ．12π或18πD ．12π或27π【解析】解：绕着3cm 的边为轴，旋转一周所得到的是底面半径为2cm ，高为3cm 的圆柱体，因此体积为232312()cm ππ⨯⨯=；绕着2cm 的边为轴，旋转一周所得到的是底面半径为3cm ，高为2cm 的圆柱体，因此体积为233218()cm ππ⨯⨯=，故选：C ．16．（2022秋•武侯区校级期中）图中的大矩形长8厘米、宽6厘米，小矩形长4厘米、宽3厘米，以长边中点连线（图中的虚线）为轴，将图中的阴影部分旋转一周得到的几何体的表面积为 平方厘米．【解析】解：由题意可得：大圆柱的侧面积28648cm ππ=⨯⨯=；小圆柱的侧面积24312cm ππ=⨯⨯=；大圆柱上下圆的面积为：22432ππ⨯=，所以几何体的表面积248123292cm ππππ=++=．故答案为：292cm π．17．（2022秋•山亭区校级月考）在长方形ABCD 中，4AB =，3BC =，以边所在直线为轴旋转一周所得几何体的体积是 .（结果保留)π【解析】解：①当3r =，4h =时，圆柱体积23436ππ=⨯⨯=；②当4r =，3h =时，圆柱体积24348ππ=⨯⨯=．几何体的体积为：36π或48π．故答案为：36π或48π．18．（2022秋•南海区期中）如图，有一长为8cm ，宽为4cm 的长方形纸板，现绕它的一边所在的直线旋转一周后，得到一个几何体，问所得几何体的形状是什么？并求所得几何体的体积．（结果保留)π【解析】解：①当4r cm =，8h cm =时，2348128()v cm ππ=⨯=；②当8r cm =，4h cm =时，2384256()v cm ππ=⨯=．答：所得几何体的形状是圆柱，几何体的体积为：3128cm π或3256cm π．19．（2022秋•碑林区校级月考）如图，阴影图形是由直角三角形和长方形拼成的，绕虚线旋转一周可以得到一个立体图形，求得到立体图形的体积．2(V r h π=圆柱，213V r h π=圆锥，2r r r =⨯，结果保留)π．【解析】解：图中阴影图形旋转一周后得到的立体图形为一个圆锥和一个圆柱的组合体，圆柱的体积等于23436ππ⨯⨯=，圆锥的体积等于213263ππ⨯⨯⨯=，所以立体图形的体积等于36642πππ+=．。

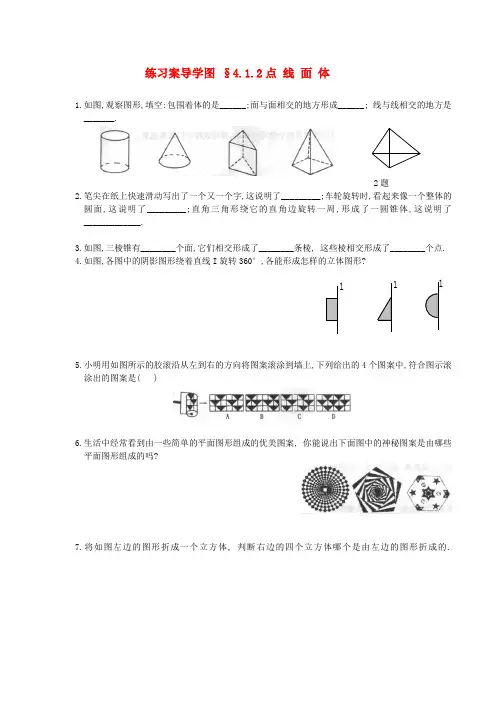
练习案导学图§4.1.2点线面体1.如图,观察图形,填空:包围着体的是______;面与面相交的地方形成______; 线与线相交的地方是_______.2题2.笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____________.3.如图,三棱锥有________个面,它们相交形成了________条棱, 这些棱相交形成了________个点.4.如图,各图中的阴影图形绕着直线I旋转360°,各能形成怎样的立体图形?l l l5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出的图案是( )6.生活中经常看到由一些简单的平面图形组成的优美图案, 你能说出下面图中的神秘图案是由哪些平面图形组成的吗?7.将如图左边的图形折成一个立方体, 判断右边的四个立方体哪个是由左边的图形折成的.*8.用6根火柴能摆成含有4个三角形的图形吗?有几种方法? 纠错栏:课后巩固训练1、把弯曲的河道改直后，缩短了河道的长度，这是因为；2.如图,线段AB上有两点C、D，则共有条线段。

3．人在雪地上走，他的脚印形成一条_______，这说明了______的数学原理；4．体是由_______围成的，面和面相交形成_______，线和线相交形成______；5．点动成________，线动成______，面动成_______；6．将三角形绕直线L旋转一周，可以得到如下图所示立体图形的是（）A B C D*7．变形题：往返于甲、乙两地的客车中途要停靠三个车站，有多少种不同的票价？要准备多少种不同的车票？纠错栏:A C D B。

人教版数学七年级上册第四章几何图形初步4.1几何图形4.1.2点、线、面、体知识梳理分点训练知识点1 点、线、面、体1. 五棱柱的顶点总个数有()A. 5个B. 10个C. 15个D. 20个2. “让子弹飞”，我们用数学知识可解释为点动成线.用数学知识解释下列现象：(1)落叶从空中划过留下的痕迹可解释为；(2)汽车车轮的运动可解释为；(3)运动员投掷铅球的路线可解释为；(4)拉上窗帘可解释为；(5)酒店旋转门旋转一周可解释为.3. 长方体是由个面围成，它有个顶点，条棱.4. 某配件公司生产的螺母配件形状如图所示.(1)这个几何体可以看做是哪几种基本的立体图形的组合?你能描述一下它的特征吗?(2)这个几何体是由哪些面组成的?知识点2 从面到体5. 一个直棱柱有12个顶点，那么它的面的个数是()A. 10个B. 9个C. 8个D. 7个6. 如图，将平面图形绕轴旋转一周，可以得到的立体图形是()A B C D7. 直角三角形的两直角边长分别为4 cm，3 cm，以其中一条直角边所在直线为轴旋转一周，得到的几何体的底面积是.8. 如图，第一排中的图形绕虚线旋转一周，能形成第二排中的某个几何体，请你把第一排与第二排中相应的图形用线连接起来.课后提升巩固训练9. 如图的几何体是由哪个图形绕铅垂线旋转一周形成的()A B C D10. 一个多面体，若顶点数为4，面数为4，则棱数是()A. 2B. 4C. 6D. 811. 在下列结论中，错误的是()A. 棱柱的侧面数与侧棱数相同B. 棱柱的棱数一定是3的倍数C. 棱柱的面数一定是奇数D. 棱柱的顶点一定是偶数12. 长方形的长为6 cm，宽为4 cm，则绕着它的宽旋转一周得到的圆柱的体积为()A. 36cm3B. 72cm3C. 96cm3D. 144cm313. 若一直棱柱有10个顶点，那么它共有条棱.14. 从棱长为2dm的正方体毛坯的一角，挖去一个棱长为1dm的小正方体，得到一个如图所示的零件，则这个零件的表面积为dm2.第14题第15题15. 如图，正方形ABCD的边长为3 cm，以AB所在的直线为轴，将正方形旋转一周，所得几何体的体积为cm3.(结果保留)16. 如图，把一长方形在直线m上翻滚，请在图中作出A点所经过的路径.17. 如图，是一个正六棱柱，它的底面边长是3 cm，高是6 cm.(1)这个棱柱的侧面积是多少?(2)这个棱柱共有多少条棱?所有的棱长的和是多少?(3)这个棱柱共有多少个顶点?(4)通过观察，试用含n的式子表示n棱柱的面数与棱的条数.18. 棱长为a的正方体摆放成如图的形状，问：(1)如图摆放成的几何体，共有几个正方体?表面积是多少?(2)如果将正方体按如图的方式摆放4层，共有几个正方体?表面积是多少?(3)若摆放成n层，那么几何体表面积又是多少?拓展探究综合训练19. 如图，左面的几何体叫三棱柱，它有5个面，9条棱，6个顶点，中间和右边的几何体分别是四棱柱和五棱柱.(1)四棱柱有个顶点，条棱，个面；(2)五棱柱有个顶点，条棱，个面；(3)你能由此猜出，六棱柱、七棱柱各有几个顶点，几条棱，几个面吗?(4)n棱柱有几个顶点，几条棱，几个面?。

4.1.3 点、线、面、体分层作业．．．．【答案】A【分析】根据面动成体以及直角梯形绕高所在直线旋转一周得圆台即可得答案.【详解】解：根据面动成体，直角梯形绕高所在直线旋转一周得圆台，故选：A．【点睛】本题考查了点、线、面、体，熟记各种常见平面图形旋转得到的立体图形是解题关键．4．如图是一个花瓶，下列平面图形绕虚线旋转一周，能形成这个花瓶表面的是（ ）A．B．C．D．【答案】C【分析】将平面图形旋转一周，再与花瓶相比较即可得出答案．【详解】解：将选项所给的平面图形绕虚线旋转一周，可得C选项符合所给图形.故选：C．【点睛】本题主要考查了点，线，面，体之间的关系，理解“面动成体”是解题的关键．5．图中是将一平面图形绕直线l旋转一周得到的，则该平面图形是（）A．B．C．D．【答案】D【分析】根据面动成体，所得图形是两个圆锥体的组合体确定答案即可．【详解】解：A、该图形绕l一周得到的图形是一个圆锥，不符合题意；B、该图形绕l一周得到的图形是一个圆锥，不符合题意；C、该图形绕l一周得到的图形是一个球，不符合题意；D、该图形绕l一周得到的图形是上下两个圆锥组成的，符合题意；故选D．【点睛】本题主要考查了面动成体，熟悉常见图形旋转得到的立体图形是解题的关键．【答案】点动成线【分析】由点，线，面，体的关系可得答案．【详解】解：节日的焰火可以看成由点运动形成的，这可以说点动成线；【答案】②【分析】根据面动成体，结合立体图形和平面图形，逐项通过旋转验证即可得到答案．A对应，B对应，C对应【答案】a d e【分析】根据面动成体的特点解答．【详解】解：a旋转得到的图形为圆锥，的组合图形，d旋转得到的图形是上面是一个圆台，下面是一个圆柱组成的组合图形，上面是一个圆锥，下面是一个圆柱组成的组合图形，∴A对应a，B对应d，c对应e，（3）解：蚂蚁可看做是点，行走的路线是线，所以一只蚂蚁行走的路线可解释为点动成线；（4）解：折扇合起来时是一条线，打开折扇得到扇面可解释为线动成面；（5）解：一个圆是面，球是立体图形，一个圆面沿着它的一条直径旋转一周成球可解释为面动成体.【点睛】此题主要考查了点、线、面、体，关键是掌握四者之间的关系．16．第一行的平面图形绕虚线旋转一周能得到第二行的一个几何体，请用线连接起来．【答案】见解析【分析】根据面动成体结合常见立体图形的形状连接即可．【详解】解：连接如图．【点睛】本题考查了点、线、面、体的知识，是基础题，熟悉常见几何体的形成是解题的关键．17．如图，某银行大堂的旋转门内部由三块宽为2m、高为3m的玻璃隔板组成．(1)将此旋转门旋转一周，能形成的几何体是圆柱．这能说明的事实___________（选择正确的一项填入）．A．点动成线B．线动成面C．面动成体(2)求该旋转门旋转一周形成的几何体的体积．（边框及衔接处忽略不计，结果保留p）【答案】(1)C(2)3p12m【分析】（1）旋转门的形状是长方形，长方形旋转一周，能形成的几何体是圆柱；（2）根据圆柱体的体积=底面积×高计算即可．【详解】（1）∵旋转门的形状是长方形，∴旋转门旋转一周，能形成的几何体是圆柱，这能说明的事实是面动成体．故答案为：C．（2）该旋转门旋转一周形成的几何体是圆柱，体积为：22312p p´´=（m3）．故形成的几何体的体积是3p．12m【点睛】本题考查了圆柱的体积的求法，掌握圆柱的体积公式，能够正确得出圆柱的底面面积是解决问题的关键．18．如图所示，有一个长为4cm、宽为3cm的长方形．(1)若分别绕它们的相邻两边所在的直线旋转一周，会得到不同的几何体，请你画出这两个几何体．(2)在你画出的这两个几何体中，哪个体积大？【答案】(1)见解析(2)第二个圆柱体的体积大【分析】（1）根据题意画出图形即可求解；（2）根据图形计算体积即可求解．【详解】（1）解：如图所示：（2）绕4cm 长的边旋转一周所得圆柱的体积333436πcm p =´´=；绕3cm 长的边旋转一周所得圆柱的体积234348πcm p =´´=．答：第二个圆柱体的体积大．【点睛】本题考查了画平面图形旋转而成的立体图形，求圆柱体的体积，熟练掌握基本立体图形是解题的关键．(1)将直角三角形ABC绕三角形的边所在的直线旋转一周，能得到(2)分别计算绕三角形直角边所在的直线旋转一周，得到几何体的体积．【答案】(1)3(2)以AB为轴得到的圆锥的体积为24．仔细观察下面的正四面体、正六面体、正八面体，解决下列问题：。

参考答案1. B【解析】一个五棱柱由两个五边形的底面和五个长方形的侧面组成，它有10个顶点.故选B.2. (1)点动成线(2)线动成面(3)点动成线(4)线动成面(5)面动成体3. 6812【解析】根据长方体的特征知，长方体是由6个面围成，它有8个顶点，12条棱.4. 解：(1)这个几何体可以看做是正六棱柱及圆柱组成，这个图形是一个六棱柱，中间是一个空的圆柱.(2)侧面是6个长方形，上下两个面是中间为圆的正六边形，中间是一个曲面.5. C【解析】直棱柱有12个顶点，一定是六棱柱，所以它有6个侧面和2个底面共8个面.故选C.6. C【解析】将平面图形绕轴旋转一周得到的立体图形是圆柱和圆锥的组合体.故选C.7. 9π cm2或16π cm2【解析】由题意知，以其中一条直角边所在直线为轴旋转一周所得，几何体为圆锥，底面是圆，底面半径为3或4 cm，所以，底面面积为9π cm2或16π cm2.8. 解：如图所示.9. A【解析】选项A旋转一周形成圆台，故A正确；选项B旋转一周形成的图形是圆柱与圆锥的组合体，故B错误；选项C旋转一周形成球，故C错误；选项D旋转一周形成圆锥，故D错误.故选A.10. C【解析】由顶点数和面数都是4知，该几何体为三棱锥，棱数为6.故选C.11. C【解析】选项A棱柱的侧面数与侧棱数相同，故A正确的；选项B棱柱的棱数有3n条，一定是3的倍数，故B正确；选项C四棱柱的面数是6，是偶数，故C错误；选项D棱柱的顶点有2n 个，一定是偶数，故D正确.故选C.12. D【解析】圆柱的体积为π×62×4=π×36×4=144π(cm3).故选D.13. 15【解析】有10个顶点的直棱柱是五棱柱，所以它有15条棱.14. 24【解析】挖去一个棱长为1dm的小正方体，得到的图形与原图形表面积相等，则表面积是2×2×6=24dm2.15. 27π【解析】直线AB为轴，将正方形旋转一周可得圆柱体，圆柱的高为3 cm，底面半径为3 cm，所以所得几何体的体积为32×π·3=27π(cm3).16. 解：如图所示.17. 解：(1)正六棱柱的侧面积3×6×6=108(cm2).(2)这个棱柱共有6＋6＋6=18条棱. 所有的棱长的和是12×3＋6×6=36＋36=72(cm).(3)这个棱柱共有12个顶点.(4)n棱柱的面数是(n＋2)面，n棱柱棱的条数是3n条.18. 解：(1)题图中1＋3＋6=10个正方体，由题可知上下左右前后露出的面都为6个正方形，该物体的表面积为6×6a2=36a2.(2)根据以上分析可得：如果将正方体按如图的方式摆放4层，则4层共有1＋3＋6＋10=20个正方体，表面积为(1＋2＋3＋4)×6a2=60a2.(3)由题意知，从正面看到的正方形个数有(1＋2＋3＋4＋…＋n)=12n n(个)，表面积为12n n×6a2=612n na2=3n(n＋1)a2.。

4.1.2点、线、面、体
乡士的难题
朝圣者的行列中有乡士。

一天，当全体同伴来到一家名为"跳棋"
的小店前面时，那门口挂着一个象棋盘作为广告。

乡士决定向旅伴们炫耀自己的技艺，他挑出九支箭说: "请注意，亲爱的老爷们，我把这些箭射到这个棋盘的九个方格上，并且，无论哪一支箭都不与别的箭位于同一直线上。

"
如上图所示，他确实做到了，没有两支箭是在同一横行、竖列、对角线上。

这位乡士继续说:
"这就是给你们的难题:请移动三支箭到其相邻的一格内，使得这九支箭新摆的位置仍然保持没有两支箭在同一横行、竖列、对角线上。

"（注:所谓"相邻"的格子，是原来格子的上、下、左、右、斜等八个方向的任一邻格。

）
答案
如图所示，在那个"跳棋"旅店的象棋盘上移动三支箭，就能使任何一行、列都只有一支箭。

黑点标记着所移箭头原来的位置。

点、线、面、体
轻松入门
1.如图,观察图形,填空:包围着体的是______;面与面相交的地方形成______; 线与线相交的地方是
_______.
2.笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起
来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____________.
3.如图,三棱锥有________个面,它们相交形成了________条棱, 这些棱相交形成了
________个点.
4.如图,各图中的阴影图形绕着直线I旋转360°,各能形成怎样的立体图形?
快乐晋级
5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出
的图案是( )
6.生活中经常看到由一些简单的平面图形组成的优美图案, 你能说出下面图中的神秘图案是由哪些平面
图形组成的吗?
7.将如图左边的图形折成一个立方体, 判断右边的四个立方体哪个是由左边的图形折成的.
8.用6根火柴能摆成含有4个三角形的图形吗?有几种方法?
拓广探索
9.小明为班级专栏设计一个图案,如图,主题是“我们喜爱合作学习”, 请你也尝试用圆、扇形、三角形、
四边形、直线等为环保专栏设计一个图案, 并标明你的主题.
我们喜爱合作学习
答案
1.面;线;点
2.点动成线;线动成面;面动成体
3.4;6;4
4.圆柱;圆锥;球
5.A 7.(1)B;(2)B;(3)B 8.提示:三棱锥。

点线面练习1、夜里将点燃的蚊香迅速绕一圈,可划出一个曲线,这是因为( )A、面对成体B、线动成面C、点动成线D、面面相交成线2、用钢笔写字是一个生活中的实例,用数学原理分析,它所属于的现象是( )A、点动成线B、线动成面C、线线相交D、面面相交3、我们已经认识了"点动成线,线动成面,面动成体"的数学事实,以下现象:"夜晚的流星划过天空时留下一道明亮的光线",这说明了_________的数学事实.4、汽车的雨刷把玻璃上的雨水刷干净属于的实际应用是( )A、点动成线B、线动成面C、面动成体D、以上答案都不对5、生活中我们见到的自行车的辐条运动形成的几何图形可解释为( )A、点动成线B、线动成面C、面动成体D、以上答案都不对6、汽车的雨刷把玻璃上的雨水刷干净,是属于( )的实际应用.A、点动成线B、线动成面C、面动成体D、以上答案都不对7、看到飞行中的萤火虫,可以说明( )A、点动成线B、线动成面C、面动成体D、不能说明什么问题8、下列现象能说明"面动成体"的是( )A、天空划过一道流星B、旋转一扇门,门在空中运动的痕迹C、抛出一块小石子,石子在空中飞行的路线D、汽车雨刷在挡风玻璃上刷出的痕迹9、用运动的观点来理解点,线,面,体.点动成_________,线动成_________,面动成_________.拿一枚硬币,将其立在桌面上用力一转,它形成的是一个_________体,由此说明_________。

圆规在纸上划过会留下一个封闭的痕迹,这种现象说明_________。

一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快地旋转起来时就会看到一个球,这种现象说明_________。

冬天环卫工人使用下部是长方形的木锨推雪时,木锨过处,雪就没了,这种现象说明_________。

必修2点线面基训思维拓展部分习题解答：P24：已知正方体ABCD-A1 B1C1 D1中，E，F分别为D1 C1，C1 B1的中点，AC∩BD=P，A1 C1∩EF=Q。

求证：（1）D，B，F，E四点共面；（2）若A1 C交平面DBFE于R点，则P，Q，R三点共线。

P26：如图，正方体ABCD -A1 B1C1 D1中，（1）求AC与A1D所成角的大小；（2）求A1C与所成角的大小；（3）若F，E分别为AB，的中点，求A1 C1与EF所成角的大小；（4）求A D1与EF所成角的大小。

P28：在正方体A C1中，E是CD的中点，连接AE并延长与BC的延长线交于点F，连接BE并延长交AD的延长线于点G，连接FG。

求证：FG 直线平面ABCD且直线FG ∥A1 B1。

P31：如图，在棱长为a的正方体ABCD-A1 B1中，E,F,P,Q分别是BC, A D1,BD的中点.(1)求证：PQ∥平面DC C1 D1;(2)求PQ的长;(3)求证：EF∥B B1D1 D平面.P33：如图，空间四边形ABCD的对棱AD，BC成60°角，且AD=BC=a，平行于AD与BC的截面分别交AB，AC，CD，BD 于E，F，G，H。

（1）求证：四边形EFGH为平行四边形。

（2）E在AB的何处时截面EFGH的面积最大？最大面积是多少？P36：如图，已知⊿ABC是正三角形，EA，CD都垂直于平面ABC，且EA=AB=2a，DC=a，F是BC的中点，求证：（1）FD平面ABC；（2）AF⊥平面EDB。

P38：如图，已知⊿ABC是等边三角形，EC⊥平面ABC，BD ⊥平面ABC，且EC，DB在平面ABC的同侧，M为EA的中点，CE=2BD，求证：（1）DE=DA；（2）平面BDM⊥平面ECA；（3）平面DEA⊥平面ECA。

P41：如图，ABCD是边长为a的菱形，∠A=60°，PC⊥平面ABCD，E是PA的中点，求证：（1）平面BDE⊥平面ABCD；（2）求点E到平面PBC的距离。