412点线面体

立体构成的基本形态要素-——点、线、面、体一、点的构成1、造型中的点具有相对性。

2、点的构成方式很多,但点独立存在的构成少,多数情况下会存在其他形态要素.3、点的视觉情感及特征点的特征: a。

与环境相比较，体积小b。

长度、宽度、高度近似点的作用： a.起某种稳定图式、造型的作用b。

创造视觉焦点c。

创造运动感：设计作品中点的动感通常源于点的集群关系和点与背景的图底关系。

二、线材的构成1、线的形态与感情象征直线与曲线是构成线的两大系统，也是决定一切由线构成的形的基本要素. 一般来说，直线表示静,曲线表示动.直线是一种无机线，它具有冷淡而坚强的表现力。

其中垂直线具有生命、尊严、永恒、上升、下落等感情象征;水平线趋向于表示平静、安定、向上的感情象征;斜直线意味着运动、积极、阳性等感情色彩；向下的斜直线则有危险、消极、阴性等感觉特质。

而曲折线则表示不安的象征性联想。

2、材料的连接点称为节点,节点有三种滑节-—可以在接触面上自由滑动或滚动。

铰节——像铰链一样可以上下左右旋转，但不能移动，具有各方向受力的特性。

刚节-—完全固定死的。

线材构成中，线材大致可分为软质线材（又称拉力材）和硬质线材(又称压缩材）两大类。

软质线材包括棉、麻、丝、绳、化纤等软线,还有铁、钢、铝丝等可弯曲变形的金属线材；硬质线材有木、塑料及其他金属条材等。

(1)软质线材的构成利用棉、麻、丝、化纤等软线、软绳。

在构成中，按意图制作造型框架.其结构可选用正方体、三角柱、三角锥、五棱柱、六棱柱等造型;也可采用正圆、半圆或渐伸涡线形等、并在框架上面竖立支柱，以小钉为连点进行连接构成。

（2)硬质线材构成木条、金属条、塑料细管、玻璃柱等线材均可用以组合而成为立体造型。

在构成前，先确定好支架.构成后，部分撤掉，只保留硬质线材构成的部分。

常见的造型方法有：a．垒积构造只把材料重叠起来做成立体的构造物,叫做累积形式的构成。

在制作时应该注意：（1）接触面过分倾斜易引起滑动；整体的重心若超过底部的支撑面则构造物将因失去平衡而倒塌.(2）与用线材做立体构成—样,不要忘记使空隙大小具有韵律.(3）作为垒积构造的变形，可以在结合部施以简单的防滑处理（如缺口等），这样将出现更多的变化。

点线面与体点线面与体的基本概念与特征点线面与体是几何学中的基本概念，它们是描述和构建几何图形和空间的基本要素。

本文将介绍点线面与体的基本概念与特征，并讨论它们在几何学中的重要性。

一、点的概念与特征点是几何学中最基本的概念之一，它没有长度、宽度和高度，只有位置。

点可以表示为一个具体的坐标或一种抽象的符号，如(x, y, z)或A。

无论如何表示，点都是几何空间中的一个具体位置。

点有以下几个特征：1. 点是零维的，没有尺寸和形状。

2. 点没有方向，可以在空间中移动，但它的位置始终不变。

3. 两个不同点之间可以通过直线连接。

二、线的概念与特征线是由一系列点连接而成的几何对象，它有长度但没有宽度和高度。

线是由无数个点构成的，可以通过这些点的连续性来描述一个曲线或直线。

线有以下几个特征：1. 线是一维的，有长度但没有宽度和高度。

2. 线无论怎样延长都没有尽头，可以无限延伸。

3. 线可以是直线或曲线，直线是两个点之间的最短路径，而曲线则不是。

三、面的概念与特征面是由一系列线连接而成的几何对象，它有长度和宽度但没有高度。

面可以看作由无数个点和线组成的一个平坦的二维区域。

面有以下几个特征：1. 面是二维的，有长度和宽度但没有高度。

2. 面可以是平面或曲面，平面可以由至少三个相互连接的点所确定，而曲面则不是。

3. 面可以被划分为许多小区域，每个小区域都可以表示为一个点、线或面。

四、体的概念与特征体是由一系列面连接而成的几何对象，它有长度、宽度和高度。

体是空间中的一个三维区域，可以看作由无数个点、线和面组成的一个立体物体。

体有以下几个特征：1. 体是三维的，在长度、宽度和高度上都有尺寸。

2. 体是由至少四个面连接而成的，每个面都可以表示为一个点、线或面。

3. 体可以是正体或曲体，正体的面都是平面，而曲体则不是。

点线面与体在几何学中起着重要的作用。

它们是描述和构建几何图形和空间的基本要素，为我们研究和应用几何学提供了基础。

4.1.2 点、线、面、体》教学设计广元市昭化区清水乡小学姜云兰【教学内容】新课标人教版七年级数学第四章4.1.2 点、线、面、体。

【三维目标】1、知识与技能目标：（1）．进一步认识体、面、线、点的概念。

（2）．理解点、线、面、体之间的关系。

2、过程与方法目标：（1）．通过对点、线、面、体的认识，让学生经历用图形描述现实世界的过程，用它们来解释生活中的现象。

（2）．培养学生操作、观察、分析、猜测和概括等能力，同时渗透转化、化归、变换的思想。

3、情感态度与价值观目标：通过联系现实世界中各种常见的几何体及情景，让学生认识数学与现实生活的密切联系。

【教学重、难点】重点：正确认识点、线、面、体，以及它们之间的关系。

难点：点动成线、线动成面、面动成体的活动以及数学与现实生活的联系。

教学方法】1观察法。

培养学生观察联想的能力，学生通过观察丰富的图片、实物, 联想这些几何图形与实际图形的关系。

2. 操作法。

培养学生动手操作的能力。

3. 讨论法。

培养学生自主探究、合作交流的能力。

4. 多媒体电化教学。

通过观察实物，在观察、实践中感知几何图形是由点、线、面、体组成，再利用课件动态演示让学生从另外一个角度对所学知识进行再认识.让学生从感性认识上升到理性认识。

【教学准备】几何体的旋转学具、多媒体课件。

【教学过程】中的一些实例吗？2:（课件展示）扇子展开的动画3:（课件演示动画实例：圆锥体、球、圆台的形成。

）归纳：动态时点、线、面、体的关系点动成------ 线线动成------ 面面动成------ 体展开后就成了面。

这说明----- 。

生活中还有这样的实例吗？（2）线动成面做一做：1）长方形纸片绕它的一边旋转形成了一个，这说明。

2）直角三角形绕它的一直角边旋转形成了------ 。

3）半圆绕它的直径旋转形成了。

（学习小组分工，一个同学旋转你们准备的学具，其他同学观察得出结论。

）（3）面动成体连一连、把下面第一行的平面图形绕线旋转一周，便能形成第二行的某个几何体，请用虚线连接：主探索的过程中获得知识和技能，掌握基本的数学思想方法。

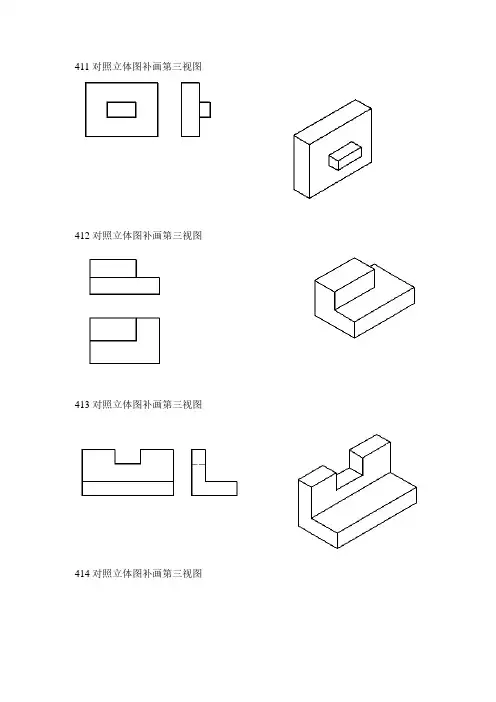
411对照立体图补画第三视图412对照立体图补画第三视图413对照立体图补画第三视图414对照立体图补画第三视图421已知各点的空间位置，试作投影图，并填写出各点距投影面的位置（单位：mm）。

422已知各点的空间位置，试作投影图，并填写出各点距投影面的位置（单位：mm）。

431画出各点的空间位置432求下列各点的第三面投影，并填写出各点距投影面的距离。

433已知各点的坐标值，求作三面投影图。

441已知点A的三面投影，并知点B在点A正上方10mm，点C在点A正右方15mm。

求两点B、C的三面投影图。

442已知各点的投影，试判断各点与点A的位置，并对投影图中的重影点判别可见性。

443已知各点的三面投影，填写出各自的坐标值。

451已知直线上两端点A（30，25，6）、B（6，5，25），作出该直线的三面投影图。

452已知直线AB上一点C距H面20mm，求点C的V、H面投影。

453在直线AB上有一点C，且AC∶CB=1∶2，作出点C的两面投影。

461判别下列各直线对投影面的相对位置，并补画第三面投影。

462判别下列各直线对投影面的相对位置，并补画第三面投影。

471求线段AB的实长及对3个投影面的夹角α、β、γ。

472在线段AB上取一点C，令AC=20mm，确定点C的投影。

473已知B 点距H 面30mm ，求AB 的正投影。

481已知b a ''、a 及AB =45mm ，完成线段AB 的水平投影。

482判断两直线的相对位置。

491判别交叉两直线的重影点及可见性。

492已知e ，试过点E作一直线EF，令EF既与AB平行又与CD相交。

493过点K作一直线，使之与直线AB垂直相交。

4101求点M到直线AB的真实距离。

4102作一直线MN，使之与两已知直线AB、CD均垂直相交。

4103已知平面ABCD为矩形，完成其两面投影。

4111已知点K是平面ABCD上的点，求其另一面投影。

4112已知平面内点K的一个投影，求另一投影。