初升高衔接数学测试(附解答)
- 格式:docx
- 大小:100.54 KB
- 文档页数:17

初升高衔接数学测试(附解答)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初升高衔接数学测试(总分100分,时间90分钟)一、选择题(每题3分,共30分)1.一元二次方程x 2+x-2=0的根的情况是( )(A )有两个不相等的实数根 (B )有两个相等的实数根(C )只有一个实数根 (D )没有实数根2.已知0≠xyz ,则z z y y x x ++的值不可能为( ) (A) 1 (B) 0 (C )3 (D) —13.若关于x 的多项式x 2-px -6含有因式x -3,则实数p 的值为( ).A .-5B .5C .-1D .14.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h 随时间t 的变化规律如图所示(图中OABC 为一折线),则这个容器的形状为( ).5.不等式025423≤-+-x x x 的解集是( )A. 2≤xB.2≥xC.21≤≤xD.1≥x6.如图,在边长为2的菱形ABCD 中,∠A=60°,M 是AD 边的中点,N 是AB 边上的一动点,将ΔAMN 沿MN 所在直线翻折得到ΔA ’MN ,则A ’C 长度的最小值是( )A. 7B.17-C. 2D. 73-7.已知某三角形的三边长分别为6,8,6,则该三角形的内接圆半径为( )A.6B.55 C.5 D. 554 8.如图7所示,P 是等腰直角△ABC 外一点,把BP 绕点B 顺时针旋转90°到BP ′,已知∠AP ′B=135°,P ′A :P ′C=1:3,则P ′A :PB=:[ ]。
A .1:21/2;B .1:2;C .31/2:2;D .1:31/2。
9.如果关于x 的不等式组:⎩⎨⎧≤-≥-0203b x a x ,的整数解仅有1,2,那么适合这个不等式组的整数a ,b 组成的有序数对[a ,b]共有( )个。
A.8B.7C.6D.510.设1x ,2x 是一元二次方程2320x x --=的两个实数根,则2211223x x x x ++的值为( ).A. 7B.8C.9D.6二、填空题(每题4分,共20分)图7F E O DB A DC 第12题11.若,x y为实数,且20x +=,则2010()x y +的值为___________.12.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为2cm ,∠A =120°,则EF = cm .13.已知当1x =时,22ax bx +的值为3,则当2x =时,2ax bx +的值为_______.14.已知关于x 的分式方程111=--++x k x k x 的解为负数,则k 的取值范围是 。

初升高数学衔接带答案一、选择题1. 已知函数\( f(x) = 2x^2 - 3x + 5 \),求\( f(2) \)的值。
A. 7B. 9C. 11D. 13答案:B2. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
A. 5B. 6C. 7D. 8答案:A3. 一个数列的前三项为1, 2, 3,且每一项都是前一项的两倍加一,求第4项的值。
A. 7B. 8C. 9D. 10答案:A二、填空题1. 计算\( \sqrt{64} \)的值是______。
答案:82. 一个圆的半径为7,求该圆的面积。
面积公式为\( A = \pi r^2 \),所以面积是______。
答案:\( 49\pi \)三、简答题1. 解释什么是二项式定理,并给出一个例子。
答案:二项式定理是代数学中的一个重要定理,它描述了(a+b)^n展开成多项式的形式。
例如,\( (x+y)^2 = x^2 + 2xy + y^2 \)。
2. 给定一个函数\( g(x) = 3x - 4 \),求\( g^{-1}(x) \)。
答案:为了求\( g^{-1}(x) \),我们首先设\( y = g(x) \),即\( y = 3x - 4 \)。
解出x,得到\( x = \frac{y+4}{3} \),所以\( g^{-1}(x) = \frac{x+4}{3} \)。
四、计算题1. 解不等式\( |x - 5| < 2 \)。
答案:解这个绝对值不等式,我们得到两个不等式:\( -2 < x - 5 < 2 \)。
解这两个不等式,我们得到\( 3 < x < 7 \)。
2. 计算\( \int_{0}^{1} (3x^2 + 2x) \, dx \)。
答案:首先找到被积函数的原函数,即\( F(x) = x^3 + x^2 \)。
然后计算定积分:\[ \int_{0}^{1} (3x^2 + 2x) \, dx = F(1) - F(0) = (1^3 + 1^2) - (0^3 + 0^2) = 1 + 1 = 2 \]。

初升高衔接数学题详解及答案一、选择题1. 已知函数f(x) = 2x + 3,求f(-1)的值。
A. -1B. 1C. -5D. 5答案:C解析:将-1代入函数f(x)中,得到f(-1) = 2*(-1) + 3 = -2 + 3 = 1,但选项中没有1,因此正确答案应为C。
2. 如果一个数的平方等于该数本身,那么这个数可能是:A. 0B. 1C. -1D. 所有选项答案:D解析:一个数的平方等于该数本身的情况有两种:0的平方是0,1的平方是1。
因此,选项A和B都是正确的。
同时,-1的平方也是1,所以选项C也是正确的。
因此,正确答案是D。
二、填空题1. 若a + b = 5,a - b = 3,求a和b的值。
答案:a = 4,b = 1解析:将两个方程相加得到2a = 8,解得a = 4。
将a的值代入其中一个方程,例如a + b = 5,得到4 + b = 5,解得b = 1。
2. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
答案:5解析:根据勾股定理,直角三角形的斜边长度等于两条直角边的平方和的平方根,即c = √(3^2 + 4^2) = √(9 + 16) = √25 = 5。
三、解答题1. 某工厂生产一批产品,原计划每天生产100件,实际每天生产120件。
如果原计划生产20天,实际生产了多少天?答案:实际生产了15天。
解析:原计划生产的总件数为100件/天 * 20天 = 2000件。
实际每天生产120件,所以实际生产天数为2000件 / 120件/天 = 16.67天。
由于生产天数必须是整数,所以实际生产了15天。
2. 一个水池,如果同时打开A、B两个水龙头,注满水池需要2小时。
如果只打开A水龙头,注满水池需要3小时。
现在先打开B水龙头,1小时后关闭B水龙头,然后打开A水龙头,问还需要多少时间才能注满水池?答案:还需要2小时。
解析:设水池的总容量为C。
A水龙头1小时注水量为C/3,B水龙头1小时注水量为C/2 - C/3 = C/6。

初升高数学衔接试题卷答案一、选择题1. A2. C3. B4. D5. E二、填空题6. 37. √28. 2x + 3y = 129. 45°10. √3三、计算题11. 解:原式 = (x + 2)(x - 3) = x^2 - x - 6。
12. 解:原式= √(25 + 10√2) = √((5 + √2)^2) = 5 + √2。
13. 解:原式 = (2a^2 - 3a + 1)(2a^2 + 3a - 1) = 4a^4 - 9a^2 + 1。
四、解答题14. 解:设三角形ABC的三边长分别为a, b, c,根据余弦定理,有: c^2 = a^2 + b^2 - 2ab*cosC代入已知的a, b, C的值,可得c的值。
15. 解:设函数f(x) = ax^2 + bx + c,根据已知条件,可列出方程组:f(0) = c = 0f(1) = a + b + c = 2f(-1) = a - b + c = -1解方程组可得a, b的值,进而得到f(x)的表达式。
16. 解:设圆的方程为(x - h)^2 + (y - k)^2 = r^2,根据圆心和半径,可得h, k, r的值,进而得到圆的方程。
五、证明题17. 解:要证明三角形ABC是等边三角形,需要证明三边相等,即证明a = b = c。
根据已知条件,可列出方程组:a^2 = b^2 = c^2解方程组可得a, b, c的值,进而证明三角形ABC是等边三角形。
六、应用题18. 解:设购买x个苹果,y个橙子,根据题目条件,可列出方程组: x + y = 102x + 3y = 31解方程组可得x, y的值,进而得到购买苹果和橙子的数量。
19. 解:设甲乙两地相距d千米,根据速度和时间的关系,可列出方程:d = v1 * t1 + v2 * t2代入已知的v1, t1, v2, t2的值,可得d的值。
20. 解:设投资x万元,根据利润和投资额的关系,可列出方程:P = k * x - c代入已知的k, c的值,可得x的值,进而得到投资额。

初升高数学衔接试卷及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 0.33333...(无限循环)B. πC. √2D. 1/32. 一个圆的半径为5,那么它的直径是多少?A. 10B. 15C. 20D. 253. 如果一个二次方程 \( ax^2 + bx + c = 0 \) 有两个相等的实根,那么 \( b^2 - 4ac \) 等于多少?A. 0B. 1C. -1D. 44. 函数 \( y = 3x + 2 \) 的斜率是多少?A. 2B. 3C. 5D. 45. 以下哪个表达式是正确的因式分解?A. \( x^2 - 1 = x + 1 \)B. \( x^2 - 1 = x - 1 \)C. \( x^2 - 1 = (x + 1)(x - 1) \)D. \( x^2 - 1 = (x - 1)^2 \)6. 一个三角形的三边长分别是3,4,5,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能构成三角形7. 一个数的平方根是2,那么这个数是:A. 4B. -4C. 2D. -28. 如果一个函数 \( f(x) \) 是奇函数,那么 \( f(-x) \) 等于:A. \( f(x) \)B. \( -f(x) \)C. \( x \cdot f(x) \)D. \( x^2 \cdot f(x) \)9. 以下哪个选项是不等式 \( x^2 - 4x + 3 < 0 \) 的解集?A. \( x < 1 \) 或 \( x > 3 \)B. \( x < 3 \) 或 \( x > 1 \)C. \( 1 < x < 3 \)D. \( x < -3 \) 或 \( x > 1 \)10. 一个数列的前5项为1,3,5,7,9,这个数列是:A. 等差数列B. 等比数列C. 既不是等差数列也不是等比数列D. 几何数列二、填空题(每题2分,共20分)11. 一个直角三角形的两条直角边长分别是6和8,那么斜边长是________。

初升高衔接数学题加答案一、选择题(每题3分,共30分)1. 若a、b、c是三角形的三边长,且满足a^2 + b^2 = c^2,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不规则三角形答案:B2. 已知x^2 - 5x + 6 = 0,求x的值。
A. x = 2B. x = 3C. x = -2D. x = -3答案:B3. 一个数列的前三项为1,2,3,若每一项都等于前一项的平方,那么第四项是:A. 4B. 8C. 9D. 16答案:C4. 一个圆的半径为r,圆心到圆上任意一点的距离都等于r,这个圆的面积是:A. πr^2B. 2πrC. r^2D. 2r^2答案:A5. 若函数f(x) = 2x - 3,求f(5)的值。
A. 7B. 4C. 2D. 1答案:A6. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∪B的结果。
A. {1, 2, 3}B. {1, 2, 3, 4}C. {2, 3}D. {1, 2, 3, 4, 5}答案:B7. 一个数的平方根是4,这个数是:A. 16B. -16C. 8D. -8答案:A8. 一个直角三角形的两条直角边分别为3和4,斜边的长度是:A. 5B. 6C. 7D. 8答案:A9. 一个二次方程x^2 + 2x + 1 = 0的解是:A. x = -1B. x = 1C. x = -2D. x = 2答案:A10. 若a和b互为相反数,且a + b = 0,那么a的值是:A. 0B. 1C. -1D. 无法确定答案:D二、填空题(每题2分,共20分)1. 若一个数的立方等于-27,则这个数是______。
答案:-32. 一个数的绝对值是5,则这个数可以是______或______。
答案:5 或 -53. 一个直角三角形的斜边长为5,若一条直角边长为3,则另一条直角边长为______。
答案:44. 若a = 3b,且b ≠ 0,则a和b的比例是______。

第二章:一元二次函数、方程和不等式综合检测卷(试卷满分150分,考试用时120分钟)一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.(23-24高一下·河南开封·期中)不等式220x x +-<的解集为( )A .{21}x x -<<∣B .{12}x x -<<∣C .{2xx <-∣或1}x >D .{1x x <-∣或2}x >2.(23-24高一上·湖南衡阳·月考)若2x >-,则12y x x =++的最小值为( )A .-2B .0C .1D .123.(23-24高一上·广东珠海·期中)已知25P a =+,41Q a =+,则P ,Q 的大小关系是( )A .P Q<B .P Q>C .P Q≤D .P Q≥4.(23-24高一上·江苏盐城·月考)已知实数x ,y 满足41x y -≤-≤-,145x y -≤-≤,则9x y -的取值范围是( )A .[7,26]-B .[1,20]-C .[]4,15D .[]1,155.(23-24高一上·湖南衡阳·月考)已知不等式230ax x b +->的解集为{}12x x -<<,则a 、b 的值等于( )A .3a =,6b =-B .3a =,6b =C .3a =-,6b =-D .3a =-,6b =6.(23-24高一上·贵州黔南·月考)已知,0x y >且41x y +=,则11x y +的最小值为( )A .B .8C .9D .107.(23-24高一下·河南·月考)若命题“x ∃∈R ,20x ax a --≤”为假命题,则实数a 的取值范围是( )A .(,4][0,)-∞-+∞B .(,4)(0,)∞∞--⋃+C .[]4,0-D .()4,0-8.(23-24高一上·广东广州·月考)一家金店使用一架两臂不等长的天平称黄金.一位顾客到店内购买20g 黄金,店员先将10g 的砝码放在天平左盘中,取出一些黄金放在天平右盘中,使天平平衡;再将10g 的砝码放在天平右盘中,再取出一些黄金放在天平左盘中,使得天平平衡;最后将两次称得的黄金交给顾客.记顾客实际购得的黄金为xg ,则x 与20的大小关系为( )A .20x <B .20x >C .20x =D .无法确定二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.(23-24高一上·江苏苏州·月考)若0a b <<,则下列结论正确的是( )A .11a b>B .01a b<<C .2ab b >D .b a a b>10.(22-23高一上·山西大同·月考)下列结论正确的是( )A .当0x >时,2≥B .当2x >时,1x x+的最小值是2C .当0,0x y >>时,2x y y x+≥D .当2x <时,112y x x =-+-的最小值为311.(23-24高一上·湖北武汉·月考)已知01b a <<+,若关于x 的不等式22()()x b ax ->的解集中的整数恰有3个,则a 的值可以为( )A .12-B .12C .32D .52三、填空题:本题共3小题,每小题5分,共15分.12.(23-24高一上·河北沧州·期末)不等式302x x+≥-的解集为 .13.(23-24高一上·江苏连云港·月考)已知方程22240x ax a -+-=的一个实根小于2,另一个实根大于2,求实数a 的取值范围.14.(23-24高一上·山东菏泽·月考)若两个正实数x y ,满足3x y +=,且不等式4161m x y+>+恒成立,则实数m 的取值范围为.四、解答题:本题共5小题,共77分。

初升高数学衔接题及答案【题目一:代数基础】题目:求解方程 \( x^2 - 5x + 6 = 0 \) 的根。
【答案】首先,我们可以通过因式分解来解这个方程:\( x^2 - 5x + 6 = (x - 2)(x - 3) = 0 \)。
因此,方程的根是 \( x = 2 \) 和 \( x = 3 \)。
【题目二:几何基础】题目:在直角三角形ABC中,角C是直角,AB是斜边,如果AC=6,BC=8,求斜边AB的长度。
【答案】根据勾股定理,直角三角形的斜边平方等于两直角边的平方和,即:\( AB^2 = AC^2 + BC^2 \)。
代入已知值:\( AB^2 = 6^2 + 8^2 = 36 + 64 = 100 \)。
因此,斜边AB的长度为 \( AB = \sqrt{100} = 10 \)。
【题目三:函数基础】题目:如果函数 \( f(x) = 2x - 3 \),求 \( f(5) \) 的值。
【答案】将 \( x = 5 \) 代入函数 \( f(x) = 2x - 3 \) 中,我们得到:\( f(5) = 2 \cdot 5 - 3 = 10 - 3 = 7 \)。
所以,\( f(5) \) 的值为7。
【题目四:不等式基础】题目:解不等式 \( 3x - 5 < 10 \)。
【答案】首先,我们将不等式两边加上5:\( 3x - 5 + 5 < 10 + 5 \),得到 \( 3x < 15 \)。
然后,我们将不等式两边除以3:\( \frac{3x}{3} < \frac{15}{3} \),得到 \( x < 5 \)。
所以,不等式的解为 \( x < 5 \)。
【题目五:概率基础】题目:一个袋子里有5个红球和3个蓝球,随机取出一个球,求取出红球的概率。
【答案】总共有 \( 5 + 3 = 8 \) 个球。
取出红球的概率为红球数量除以总球数,即:\( P(\text{红球}) = \frac{5}{8} \)。

初升高衔接数学测试(附解答)初升高衔接数学测试(附解答)一.填空题。
(每题3分,共30分)1. 已知函数f(x) = x^2 - 4x + 3,则f(1) = ______。
解答:f(1) = 1^2 - 4 × 1 + 3 = 1 - 4 + 3 = 0。
2. 设x = 2,则函数f(x) =x^3 - 3|x|的值为______。
解答:f(2) = 2^3 - 3 × 2 = 8 - 6 = 2。
3. 设一次函数y = kx + 3的图象过点(2, 7),则k的值为______。
解答:代入已知点得7 = k × 2 + 3,整理得k = (7 - 3)/2 = 4/2 = 2。
4. 已知x^2 + k = (x - 2)(x + 3),则k的值为______。
解答:展开右侧得x^2 + k = x^2 + x - 6,比较系数得k = -6。
5. 一个三位数的1/10是5,将这个三位数加上55后得到一个四位数,这个四位数是________。
解答:设三位数为xyz,其中x、y、z表示个位、十位和百位数字。
根据题意得到两个方程:(1)1/10 * 100 * x + 1/10 *10 * y + 1/10 * z = 5;(2)100 * x + 10 * y + z + 55 = 1000 * x+ 100 * y + 10 * z。
计算得x = 4,y = 4,z = 5,所以四位数为4445。
6. 一根绳子长45米,把它剪成3段,第一段比第二段短3米,第二段比第三段短2米,则第一段的长度是________。
解答:设第一段的长度为x,根据题意得到两个方程:(1)x + (x + 3) + (x + 3 + 2) = 45;(2)x + 5 = x + 3。
解得x = 13,所以第一段的长度是13米。
7. 甲、乙两人连续投掷硬币,甲方先开始,投得正面得1分,反面得0分;乙方投得正面得2分,反面得0分。

初升高衔接测试题姓名一、选择题(每题5分,共25分)1.下列分解因式中,错误的是( )A.)31)(31(912x x x -+=-B.22)21(41-=+-a a a C.)(y x m my mx +-=+- D.))((b a y x by bx ay ax --=+--2. 若,211=-y x 则yxy x y xy x ---+33的值为 A.53 B. 53- C.35- D. 35 3.下组比较大小中,成立的是( ) A.10111112->- B.622462->+ C.353819-<- D.23549-<- 4.若40≤≤x 时,则x x y -=的最大值与最小值分别是( )A.2,0min max -==y yB. 2,41min max -==y y C.2,22min max -=-=y y D. 0,41min max ==y y 5. 已知集合A =⎩⎨⎧⎭⎬⎫x | x ∈Z ,且32-x ∈Z ,则集合A 中的元素个数为( )A .2B .3C .4D .5 二、填空(每题5分,共25分)6.已知12-=x ,则=+-+1223x x x7.函数|1||3|+--=x x y 的最小值是8. 若集合A ={x ∈R|ax 2+ax +1=0}中只有一个元素,则a =9. 方程xx x 322=-的根的个数为 个10. 已知f ⎪⎭⎫ ⎝⎛-121x =2x -5,且f (a )=6,则a = 三、解答题(共50分)11.计算(每个2分,共8分)(1)0532⎪⎭⎫ ⎝⎛+2-2·21-412⎪⎭⎫ ⎝⎛-(0.01)0.5 (2)23×31.5×612 (3) 65312121132a b a b a b ⋅⋅⋅⎪⎪⎭⎫ ⎝⎛⋅--- (4))1)(1)(1)(1(22+-+++-x x x x x x 12.分解因式(每个4分,共12分)(1)22151112y xy x --(2)2323y y x x --+(3)611623+++x x x13.(8分)解方程:4112424=+++xx x x 14.函数研究(共12分)(1)求定义域(每个2分,共6分)①f (x )=x -4|x |-5③{}11|)12(<<-+x x x f 定义域为,求)12(-x f 的定义域(2)求函数解析式(每个3分,共6分)①已知f (x +1)=x +2x ,求f (x )的解析式.②已知f (x )是二次函数,且f (0)=0,f (x +1)=f (x )+x +1,求f (x )15.解下列不等式(10分)(1)(3分)7|41|<-x(2)(3分)321≤+x (3)(4分)03522>-+x x答案:1-5 CDCBC6. 17. -48. 49. 110. 7411.(1) 1615 (2) 6 (3) 1a (4)61x - 12.(1))53)(34(y x y x -+(2)))((22y x y xy x y x ++++- (3))3)(2)(1(+++x x x13. 1±=x14.(1) ①{}54|≠≥x x x 且 或者 [4,5)∪(5,+∞)(2)①解:法一:(换元法)设t =x +1,则x =(t -1)2,t ≥1,代入原式有f (t )=(t -1)2+2(t -1)=t 2-2t +1+2t -2=t 2-1.故f (x )=x 2-1,x ≥1.法二:(配凑法)∵x +2x =(x )2+2x +1-1=(x +1)2-1, ∴f (x +1)=(x +1)2-1,x +1≥1,即f (x )=x 2-1,x ≥1.②设f (x )=ax 2+bx +c (a ≠0),由f (0)=0,知c =0,f (x )=ax 2+bx ,又由f (x +1)=f (x )+x +1,得a (x +1)2+b (x +1)=ax 2+bx +x +1,即ax 2+(2a +b )x +a +b =ax 2+(b +1)x +1,所以⎩⎪⎨⎪⎧2a +b =b +1,a +b =1,解得a =b =12. 所以f (x )=12x 2+12x ,x ∈R. 15.(1)223<<-x (2)235-<-≥x x 或 (3)57>-<x x 或。
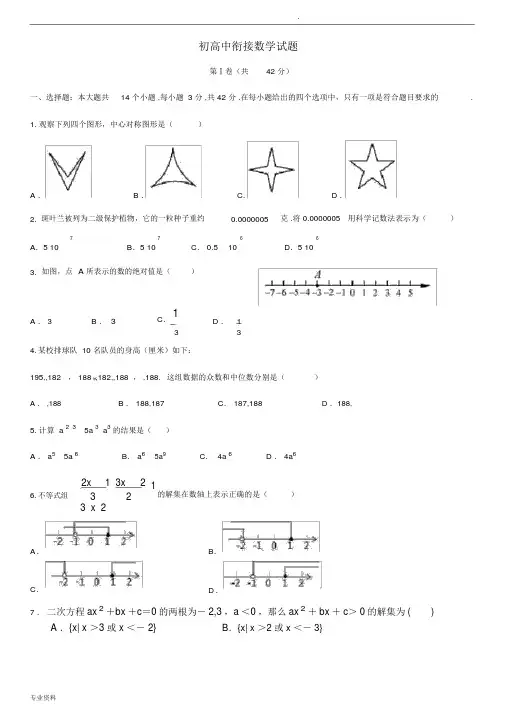
.初高中衔接数学试题第Ⅰ卷(共42 分)一、选择题:本大题共14 个小题 ,每小题 3 分 ,共 42 分 .在每小题给出的四个选项中,只有一项是符合题目要求的.1. 观察下列四个图形,中心对称图形是()A .B .C. D .2.斑叶兰被列为二级保护植物,它的一粒种子重约0.0000005克 .将 0.0000005用科学记数法表示为()77C. 0.566A.5 10B.5 1010D.5 10 3.如图,点 A 所表示的数的绝对值是()A . 3B .3C.1D .1 334.某校排球队 10 名队员的身高(厘米)如下:195,,182, 188,182,,188 , ,188.这组数据的众数和中位数分别是()A . ,188B . 188,187C. 187,188 D .188,5. 计算 a 2 35a 3 a3的结果是()A . a55a 6B. a65a9C. 4a 6 D . 4a66.不等式组A.C.2x13x213 23 x 2的解集在数轴上表示正确的是()B.D.7 .二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为()A .{x| x >3 或 x <- 2}B.{x| x >2 或 x <- 3}.C.{x | -2 <x <3} D . {x| - 3< x <2}8. 如图,三角形纸片ABC ,AB AC , BAC 90 ,点E为AB中点 . 沿过点E的直线折叠,使点 B 与点 A 重合,折痕现交于点 F .已知EF3 ,则BC的长是()2A.3 2B.3 2C. 3D.3 3 29. 如图,将线段AB 绕点 P 按顺时针方向旋转90 ,得到线段 A B ,其中点 A、 B 的对应点分别是点 A 、B ,,则点A 的坐标是()A.1,3B.4,0C. 3, 3D. 5, 110. 已知二次函数y ax 2bx c(a 0) 的图象如图所示,则正比例函y (b c) x 与反比例函数y a b c在x同一坐标系中的大致图象是().A B C D.11. 甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的 3 个扇形)做游戏 . 游戏规则:转动两个转盘各一次,当转盘停止后,指针所在概率是()1 4 52 A .B .C.D .399312 .若关于 x 的一元二次方程x 2- 2 x + k =0 有两个不相等的实数根,则 k 的取值围是()A . k < 1B . k ≤1C . k >- 1D . k > 113 .大明湖畔的“超然楼”被称作“江北第一楼” .某校数学社团的同学对超然楼的高度进行了测量.如图,他们在 A 处仰望塔顶,测得仰角为 30 °,再往楼的方向前进 60m 至 B 处,D测得仰 角为 60 °,若学生的身高忽略不计, 3 ≈1.7 ,结果精确到 1m ,则该楼的高度 CD 为()BCA第 12 题图A . 47mB . 51mC . 53mD . 54m14. 甲、乙两组各有12 名学生,组长绘制了本组 5 月份家庭用水量的统计图表,如图,比较5 月份两组家庭用水量的中位数,下列说确的是()A .甲组比乙组大B .甲、乙两组相同C .乙组比甲组大D .无法判断第Ⅱ卷(共 96 分)二、填空题(每题 3 分,满分 18 分,将答案填在答题纸上)15. 已知甲、乙两组数据的折线图如图,设甲、乙两组数据的方差分别为S 甲2、S 乙2,16. 5 月份,甲、乙两个工厂用水量共为200 吨 .进入夏季用水高峰期后,两工厂积极响应号召,采取节水措施.6月份,甲工厂用水量比 5 月份减少了15%,乙工厂用水量比 5 月份减少了10%,两个工厂 6 月份用水量共为174吨,求两个工厂 5 月份的用水量各是多少. 设甲工厂 5 月份用水量为x 吨,乙工厂 5 月份用水量为y 吨,根据题意列关于 x, y 的方程组为.17. 如图,Rt ABC, B 90 , C 30 ,O为AC上一点,OA 2 ,以 O 为圆心,以 OA 为半径的圆与CB 相切于点 E ,与 AB 相交于点 F ,连接 OE、OF ,则图中阴影部分的面积是.318.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为.819. 对于实数p , q ,我们用符号min p, q 表示 p , q 两数中较小的数,如min 1,2 1 ,因此min2,3;若min ( x1)2 , x21,则x.20.阅读理解:如图 1 ,⊙O与直线a, b都相切 . 不论⊙O如何转动,直线a,b之间的距离始终保持不变(等于⊙O 的半径).我们把具有这一特性的图形称为“等宽曲线”.图 2 是利用圆的这一特性的例子.将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用只有的方法将巨石推到金字塔顶的.拓展应用:如图 3 所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”.如图 4 ,夹在平行线c,d 之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变.若直线c, d之间的距离等于2cm ,则莱洛三角形的周长为cm .三、解答题(本大题共 5 小题,共60 分 .解答应写出文字说明、证明过程或演算步骤.)21.求下列关于 x 的不等式的解:(1)x 2-(2 m +1) x+ m 2+m < 0.(2) .求不等式 ax +1 <a2+ x 的解.22. 八年级( 1 ) 班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计请根据图息解决下列问题:( 1 )共有名同学参与问卷调查;( 2 )补全条形统计图和扇形统计图;( 3 )全校共有学生1500人,请估计该校学生一个月阅读 2 本课外书的人数约为多少.23. 某区域平面示意图如图,点O 在河的一侧,AC 和 BC 表示两条互相垂直的公路.甲勘测员在 A 处测得点 O 位于北偏东 45 ,乙勘测员在 B 处测得点 O 位于南偏西 73.7 ,测得AC840m, BC 500m .请求出点O到BC的距离 .24 ,cos73.77 ,tan 73.724参考数据:sin 73.72525724. 已知反比例函数的图象经过三个点 A 4, 3 , B 2m, y1 , C 6m, y2,其中m0 .( 1)当 y1 y2 4 时,求 m 的值;( 2)如图,过点 B、 C 分别作x轴、 y 轴的垂线,两垂线相交于点D,点P在 x 轴上,若三角形PBD的面积是8 ,请写出点 P 坐标(不需要写解答过程).25. 某公司投入研发费用80 万元( 80 万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量销售量),第一年该产品正式投产后,生产成本为 6 元/件. 此产品年销售量y (万件)与售价x ( 元/件)之间满足函数关系式 y x26 ..(2 )该产品第一年的利润为 20 万元,那么该产品第一年的售价是多少?(3 )第二年,该公司将第一年的利润 20 万元( 20 万元只计入第二年成本)再次投入研发,使产品的生产成本降为 5元/件 .为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12 万件 .请计算该公司第二年的利润W2至少为多少万元.新预科部数学试题答案1-5 CBABC6-10BCBDC11-14CABBx y2007416.17.3(1 15%) x(110%)y 1742015.___>___2 3 18.19.3; 2 或-1..20. 2 π21(1) 解 x 2- (2 m + 1) x +m 2+m < 0 ,因式分解得 (x -m )[ x - (m + 1)] < 0.∵m < m +1 ,∴m < x <m +1.即不等式的解为m <x <m + 1(2)解:将原不等式化为 (a-1) x < a2-1.①当 a-1 >0 ,即 a >1 时, x <a+1.②当 a-1 <0 ,即 a <1 时, x >a+1.③当 a-1 =0 ,即 a =1 时,不等式无解.综上所述,当 a> 1 时,不等式的解集为 x <a +1 ;当 a< 1 时,不等式的解集为 x >a +1 ;当 a= 1 时,不等式无解22 232425。
初高中数学衔接测试卷1 不等式053<--xx 的解集是_________。
2. 方程04)1(222=-+--m x m x 的两根异号,则m 的取值范围是_________。
3. 若方程01222=-+-m mx x 有两根,且方程的两根介于-2与4之间,则实数m 的取值范围是 。
4. 若不等式02<--b ax x 的解是2<x <3,则不等式012>--ax bx 的解集为 。
5.若一个正方形面积是一个正三角形面积的倍,则其边长的比为________________6.已知关于x 不等式2x 2+bx -c >0的解集为{}31|>-<x x x 或,则关于x 的不等式042≥++cx bx 的解集为_________7、已知⊙O 1的半径为1,⊙O 2的半径为2,两圆的圆心距O 1O 2为3,则两圆的位置关系是______________________8、函数xy 1=与x y =的图象在同一平面直角坐标系内的交点的个数是_________________9、2009年7月22日发生了百年不遇的天文现象——日全食,现代快报记者在安徽某地目睹了整个日全食奇观,上午9时34分看到了生光现象,此时钟面上时针与分针的夹角是________________________________________10. 某公司销售A 、B 、C 三种产品,在去年的销售中,高新产品C 的销售金额占总销售金额的40%.由于受国际金融危机的影响,今年A 、B 两种产品的销售金额都将比去年减少20%,因而高新产品C 是今年销售的重点.若要使今年的总销售金额与去年持平,那么今年高新产品C 的销售金额应比去年增加 %.11、 a 、b 为实数,且ab =1,设P =11a b a b +++,Q =1111a b +++,则P Q (填“>”、“<”或“=”). 12、. 观察下列各式:11111323⎛⎫=- ⎪⨯⎝⎭,111135235⎛⎫=- ⎪⨯⎝⎭,111157257⎛⎫=- ⎪⨯⎝⎭,…,根据观察计算:1111133557(21)(21)n n ++++⨯⨯⨯-+= (n 为正整数).13. 化简381--=____________ ,324- =___________; 14. 如果2a b c x y z ===,则456456a b cx y z+++-= ; 15. 如图,梯形ABCD 中,DC ∥AB ,DC =3cm ,AB =6cm ,且MN ∥PQ ∥AB ,DM =MP =PA , 则MN = ,PQ = 。
初高中衔接数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 0.33333(无限循环)B. πC. √2D. 1/32. 函数y = 2x^2 + 3x + 1的顶点坐标是:A. (-3/4, -1)B. (-1/2, -1)C. (-1, 0)D. (0, 1)3. 已知a + b = 5,a - b = 3,求a^2 + b^2的值。
A. 13B. 14C. 15D. 164. 一个圆的半径为5,求圆的面积。
A. 25πB. 50πC. 75πD. 100π5. 一个直角三角形的两直角边长分别为3和4,求斜边长。
A. 5B. 6C. 7D. 86. 以下哪个是二次方程的解?A. x = 1B. x = -1C. x = 2D. x = 37. 一个数列的前三项为2, 4, 6,这是一个:A. 等差数列B. 等比数列C. 几何数列D. 既不是等差也不是等比数列8. 已知x + y = 7,2x - y = 1,求x和y的值。
A. x = 2, y = 5B. x = 3, y = 4C. x = 4, y = 3D. x = 5, y = 29. 一个长方体的长、宽、高分别为2, 3, 4,求其体积。
A. 24B. 26C. 28D. 3010. 下列哪个是正弦函数的图像?A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线二、填空题(每题2分,共20分)11. 一个数的平方根是4,这个数是________。
12. 圆的周长公式是________。
13. 一个数的绝对值是其本身,这个数是________。
14. 一个二次方程的一般形式是________。
15. 等差数列的通项公式是________。
16. 函数y = 3x + 2的斜率是________。
17. 一个直角三角形的斜边长是13,一个直角边长是5,另一个直角边长是________。
18. 一个数的立方根是2,这个数是________。
初升高衔接试卷及答案一、选择题(每题2分,共20分)1. 以下哪个选项是正确的数学表达式?A. \( 3 + 4 = 7 \)B. \( 2^3 = 6 \)C. \( \sqrt{16} = 4 \)D. \( \frac{2}{4} = 0.5 \)2. 英语中,哪个单词的意思是“图书馆”?A. LibraryB. SchoolC. HospitalD. Museum3. 以下哪个历史事件标志着中国近代史的开始?A. 辛亥革命B. 五四运动C. 鸦片战争D. 甲午战争4. 物理中,力的单位是?A. 米B. 千克C. 牛顿D. 焦耳5. 化学中,水的化学式是?A. H2OC. O2D. CH46. 生物学中,细胞的基本结构不包括以下哪一项?A. 细胞壁B. 细胞膜C. 细胞核D. 线粒体7. 地理学中,赤道穿过的大洲是?A. 亚洲B. 欧洲C. 南美洲D. 非洲8. 政治学中,社会主义核心价值观包括以下哪些内容?A. 富强、民主、文明、和谐B. 自由、平等、公正、法治C. 爱国、敬业、诚信、友善D. 所有选项9. 语文中,以下哪个成语的意思是“比喻事情已经过去,无法挽回”?A. 亡羊补牢B. 覆水难收C. 画蛇添足D. 杯弓蛇影10. 计算机科学中,以下哪个选项是正确的文件扩展名?A. .exeB. .jpgD. 所有选项二、填空题(每题2分,共20分)11. 圆的周长公式是 \( C = \pi \times \) ________。
12. 英语中,“欢迎来到中国”可以翻译为“Welcome to________”。
13. 中国的首都是 ________。
14. 物理中,光速在真空中的速度大约是 ________ 米/秒。
15. 化学中,氧气的化学式是 ________。
16. 细胞的基本结构包括细胞膜、细胞核和 ________。
17. 地理学中,赤道是地球表面的一个 ________ 圈。
初升高数学衔接试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项不是实数?A. -3B. πC. √2D. i2. 已知函数f(x) = 2x^2 - 5x + 7,求f(1)的值。
A. 4B. 3C. 2D. 13. 如果一个直角三角形的两条直角边分别为3和4,那么斜边的长度是:A. 5B. 6C. 7D. 84. 一个数的平方根是它本身,这个数是:A. 1B. -1C. 0D. 1或-15. 以下哪个是二次方程的解?A. x = 2B. x = -2C. x = 3D. x = 1/26. 一个圆的半径是5,那么它的面积是:A. 25πB. 50πC. 75πD. 100π7. 如果一个数列的前三项是1, 3, 6,那么第四项是:A. 8B. 9C. 10D. 128. 一个函数的图象是直线y = 3x + 2,那么它的斜率是:A. 2B. 3C. 4D. 59. 对于方程x^2 - 5x + 6 = 0,判别式的值是:A. 1B. 4C. 9D. 2510. 一个抛物线方程y = x^2 + 2x - 3的顶点坐标是:A. (-1, -4)B. (-2, -5)C. (1, -4)D. (1, -2)二、填空题(每题4分,共20分)11. 一个数的相反数是-5,那么这个数是______。
12. 如果一个三角形的内角和为180°,那么一个直角三角形的两个锐角的和是______。
13. 一个二次方程ax^2 + bx + c = 0的判别式是b^2 - 4ac,当a = 1,b = -3,c = 2时,判别式的值是______。
14. 如果一个数列的通项公式是an = n^2 - 4n + 5,那么第5项a5是______。
15. 一个圆的周长是C,半径是r,那么C = ______。
三、解答题(每题10分,共50分)16. 解方程:2x^2 - 7x + 3 = 0。
17. 证明:对于任意实数x,(x - 1)^2 + 3 ≥ 2。
初升高衔接数学试题(含答案)姓名一、选择题〔每题5分,共25分〕1.以下分解因式中,错误的选项是〔 〕A.)31)(31(912x x x -+=-B.22)21(41-=+-a a a C.)(y x m my mx +-=+- D.))((b a y x by bx ay ax --=+--2. 假定,211=-y x 那么yxy x y xy x ---+33的值为 A.53 B. 53- C.35- D. 35 3.下组比拟大小中,成立的是〔 〕 A.10111112->- B.622462->+ C.353819-<- D.23549-<- 4.假定40≤≤x 时,那么x x y -=的最大值与最小值区分是〔 〕A.2,0min max -==y yB. 2,41min max -==y y C.2,22min max -=-=y y D. 0,41min max ==y y 5. 集合A =⎩⎨⎧⎭⎬⎫x | x ∈Z ,且32-x ∈Z ,那么集合A 中的元素个数为( )A .2B .3C .4D .5 二、填空〔每题5分,共25分〕 6.12-=x ,那么=+-+1223x x x7.函数|1||3|+--=x x y 的最小值是8. 假定集合A ={x ∈R|ax 2+ax +1=0}中只要一个元素,那么a =9. 方程xx x 322=-的根的个数为 个10. f ⎪⎭⎫ ⎝⎛-121x =2x -5,且f (a )=6,那么a = 三、解答题〔共50分〕11.计算〔每个2分,共8分〕(1)0532⎪⎭⎫ ⎝⎛+2-2·21-412⎪⎭⎫ ⎝⎛-(0.01)0.5 (2)23×31.5×612 (3) 65312121132a b a b a b ⋅⋅⋅⎪⎪⎭⎫ ⎝⎛⋅--- 〔4〕)1)(1)(1)(1(22+-+++-x x x x x x 12.分解因式〔每个4分,共12分〕〔1〕22151112y xy x --〔2〕2323y y x x --+〔3〕611623+++x x x13.〔8分〕解方程:4112424=+++xx x x 14.函数研讨〔共12分〕〔1〕求定义域〔每个2分,共6分〕①f (x )=x -4|x |-5③{}11|)12(<<-+x x x f 定义域为,求)12(-x f 的定义域 〔2〕求函数解析式(每个3分,共6分)①f (x +1)=x +2x ,求f (x )的解析式.②f (x )是二次函数,且f (0)=0,f (x +1)=f (x )+x +1,求f (x )15.解以下不等式〔10分〕〔1〕〔3分〕7|41|<-x〔2〕〔3分〕321≤+x 〔3〕〔4分〕03522>-+x x答案:1-5 CDCBC6. 17. -48. 49. 110. 7411.(1) 1615 (2) 6 (3) 1a (4)61x - 12.〔1〕)53)(34(y x y x -+(2)))((22y x y xy x y x ++++- (3))3)(2)(1(+++x x x13. 1±=x14.(1) ①{}54|≠≥x x x 且 或许 [4,5)∪(5,+∞)〔2〕①解:法一:(换元法)设t =x +1,那么x =(t -1)2,t ≥1,代入原式有f (t )=(t -1)2+2(t -1)=t 2-2t +1+2t -2=t 2-1.故f (x )=x 2-1,x ≥1.法二:(配凑法)∵x +2x =(x )2+2x +1-1=(x +1)2-1, ∴f (x +1)=(x +1)2-1,x +1≥1,即f (x )=x 2-1,x ≥1.②设f (x )=ax 2+bx +c (a ≠0),由f (0)=0,知c =0,f (x )=ax 2+bx ,又由f (x +1)=f (x )+x +1,得a (x +1)2+b (x +1)=ax 2+bx +x +1,即ax 2+(2a +b )x +a +b =ax 2+(b +1)x +1,所以⎩⎪⎨⎪⎧2a +b =b +1,a +b =1,解得a =b =12. 所以f (x )=12x 2+12x ,x ∈R. 15.(1)223<<-x (2)235-<-≥x x 或 (3)57>-<x x 或。
初升高数学试题附加答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 2.5B. πC. 0.3333…D. √42. 如果一个角的度数是45°,那么它的余角是多少度?A. 15°B. 30°C. 45°D. 60°3. 已知a,b,c是三角形的三边,且a + b > c,那么三角形的类型是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定4. 一个数的平方根是2,那么这个数是多少?A. 4B. -4C. 8D. 165. 一个圆的半径是5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π6. 一个数列的前四项是1, 3, 5, 7,这个数列是:A. 等差数列B. 等比数列C. 几何数列D. 既不是等差数列也不是等比数列7. 一个二次方程x² - 4x + 4 = 0的判别式是:A. 0B. 4C. 8D. 168. 一个函数f(x) = x² + 2x - 3的顶点坐标是:A. (-1, -4)B. (1, -2)C. (-1, -2)D. (1, -4)9. 一个函数y = 3x + 2的斜率是:A. 3B. 2C. -3D. -210. 如果一个多项式P(x) = x³ - 2x² + 3x - 4,那么P(1)的值是:A. -2B. -1C. 0D. 1二、填空题(每题2分,共20分)11. 一个直角三角形的两直角边分别为3和4,那么斜边的长度是________。
12. 一个数的立方根是3,那么这个数是________。
13. 如果一个圆的直径是10,那么它的周长是________。
14. 一个函数y = kx + b的斜率是k,当k________时,函数的图像是上升的。
15. 一个数的相反数是-5,那么这个数是________。
16. 如果一个多项式P(x) = ax³ + bx² + cx + d,那么P(-x) +P(x) =________。
初升高衔接数学测试
(总分100分,时间90分钟)
一、选择题(每题3分,共30分)
2
1. 一元二次方程x +x-2=0的根的情况是(
)
3.若关于x 的多项式x 2 — px —6含有因式x - 3,则实数p 的值为
( )•
A . — 5 4.均匀地向一个容器注水,最后把容器注满.在注水过程
中,水面高
度h 随时间t 的变化规律如图所示(图中 OAB (为一折线),则这
个容器的形状为( ).
(A )有两个不相等的实数
根
(B )有两个相等的实数根
2.已知xyz 0,则」
x y y| 的值不可能为(
(A) 1
( B) 0 (C ) 3 (D) — 1
5.不等式x34x25x 2 0的解集是()
A. x 2
B. x 2
C. 1 x 2
D. x 1
6. 如图,在边长为2的菱形ABC冲,/ A=60°, M是AD边的中点,
N是AB边上的一动点,将△ AMN沿MN所在直线翻折得到△ A MN则A C长度的最小值是()
D C
A. 7
B. .7 1
C. 2
D.
7. 已知某三角形的三边长分别为6, 8, 6,则该三角形的内接圆半径
为()
A. 6
B.诗
C. 5
D.
8. 如图7所示,P是等腰直角△ ABC外一点,把BP绕点B顺时针旋转90°到BP,已知
/ AP B=135, P‘ A: P‘ C=1: 3,贝S P A: PB=[]
C. 31/2: 2;
D. 1: 31/2。
9. 如果关于x 的不等式组:;::0,的整数解仅有1,2’那么适合 这个不等式组的整数a ,b 组成的有序数对[a ,b ]共有() 个。
10.设X, , X 2是一元二次方程X 2 3x 2 0的两个实数根,则X i 2 3x 1X 2 X 22
的值为().
A. 7
二、填空题(每题4分,共20 分)
11.若X , y 为实数,且X 2 y 3 0,则(X y )2010的值为
将菱形纸片ABC [折叠,使点A 恰好落在菱形的对称中心 O EF 若菱形 ABCD 的 边长为 2cm,/ A=120 °,贝 S EF =12.如图, 处,折痕为 cm .
D
B D
13・已知当x 1时,2ax 2 bx 的值为3,则当x 2时,ax 2 bx 的值为
三、解答题(每题10分,共50分)
16.作图题。
(1)如下图,有一条河河岸为 AB 和CD 小明在E 点放牛,小明的 家在F 点处,现在他要先把牛牵到河边喝水,然后再回家,在河岸边 找一点G 使得小明所走的路程最近。
简要说明作图步骤并作图。
.E
.F
14-已知关于x 的分式方程”
—1的解为负数,则k 的取值范围
x 1 15.分解因式 2y 2 3x 2 5xy x 9y
4= _________________
A __________________________________ B
C __________________________________ D
(2)作出下面函数的图像。
f(x) x 3 x 1
17.化简2m2 2m
2m 2 (齐)
18.计算
(1)(2+1)( 22+1) ( 24+1)•••(264+1)+1
I
2014 2015
19. ( 1)已知一个函数y f(x)满足2f(x) f(-) x23,求函数y
f(x)
x 八
的表达式。
(2)解三元一次方程组
x 2y z 2
2x y 3z 1
2x 3y 2z 2
20.如图,点B在线段AC上,点D , E在AC同侧, A C 90:,
BD BE , AD BC.
(1)求证:AC AD CE ;
(2)若AD 3 , CE 5,点P为线段AB上的动点,连接DP,作PQ DP , 交直线BE与点Q ;
i)当点P与A,B两点不重合时’求DQ的值;
ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路
径(线段)长.(直接写出结果,不必写出解答过程)
初升高衔接数学测试参考答案
一、选择题(每题 3 分,共30 分)
1.A
2.B
3.D
4.B
【知识点】几何最值问题
【答案】7 1
【解析】本题考查几何最值问题,因为MA在整个过程中长度不发
生变化,A'始终在以M为圆心、MA为半径的圆上,故当A为MC与
圆的交点时,A C长度的最小。
解:如图,v MD=1 / MDH=6° ,
C
••• HD』,MH=^ ,
2 2
•H C2,由勾股定理可得MC=7 ,
2
•A C长度的最小值是.7 1。
故答案为:.7 1.
8.B
10. A
二、填空题(每题4分,共20分)
11. 1
12. .3
13. 6
1厂
14. k 且k 1
2
【知识点】分式方程的解
【答案】k 1且k 1
2
【解析】求出分式方程的解x=1-2k,得出1-2k v0,求出k的范围, 根据分式方程得出1-2k半-1,求出k,即可得出答案.
解:分式方程两边同乘以(x+1)(x-1 ),并化解得:x=1-2k ,
由已知可得1-2k v 0, 1-2k工-1 ,
所以k -且k 1。
2
故答案为:k -且k 1
2
15. -(3x-y+4)(x+2y-1)
三、解答题(每题10分,共50分)
16. (1)作图步骤:(1)作点E关于AB的对称点E'
交AB于点G(3)连接EG(4)点G即为所求。
(图略)
(2)提示:去绝对值,把函数写成分段函数形式再画图。
2
仃原式二」^亠上m 1 (m 1)
' 2m(m 1) (m 1) (m 1)(m 1)
(图略)
2m 2 _ 2(m 1) (m 1)( m 1) (m 1)(m 1) (m 1)(m 1)
2 (m 1)
1
18. ( 1)原式=(2 1)(2 1)(221)...(2641)+1
2 2 4 64
= (2 1)(2 1)(2 1)...(2 1) +1
128
2
(2)原式=(1 1 11 11 1
2)(2 3) (3 1)…(而
1 2015
1 1
2014 2015
1
1 1
⑵ x 3,y t ,z
20. (1)证厶 ABD^A CEE H AB=CE
(2)如图,过 Q 作QH L BC 于点 巴则厶ADP^A HPQ △ BHQ^A BCE AD AP BH QH PH QH , BC EC
又••• P 不与A 、B 重合,• x 5,即x 5 0 ,
2015
2014
2015
19. ( 1)解:由 2f(x) f (-)
x X 3 可得 2 f (-)
x 1 f (x) —2 3,联立解二 元一次方程组可得y
f(x) 2 2
3x 2 3x
设心,QM ,则有号舟
••• BH=3y , PH 旦+5 x
5
5 3
3y ,
5 x
5 x ,即(x 5)(3y 5x) y
二3y 5x 0 即3y 5x
DP x 3
PQ y 5
(3) 口。