运筹学-线性规划模型及其解法.
- 格式:ppt
- 大小:702.00 KB
- 文档页数:2





第一章 线性规划模型线性规划(Linear Programming )是数学规划的一个重要组成部分,是最优化与运筹学理论中的一个重要分支和常用的方法,是最优化理论的基础性内容。
第一节 线性规划问题及其数学模型一、问题的提出在生产管理和经营活动中经常提出一类问题,即如何利用有限的人力、物力、财力等资源,以便得到最好的经济效果。
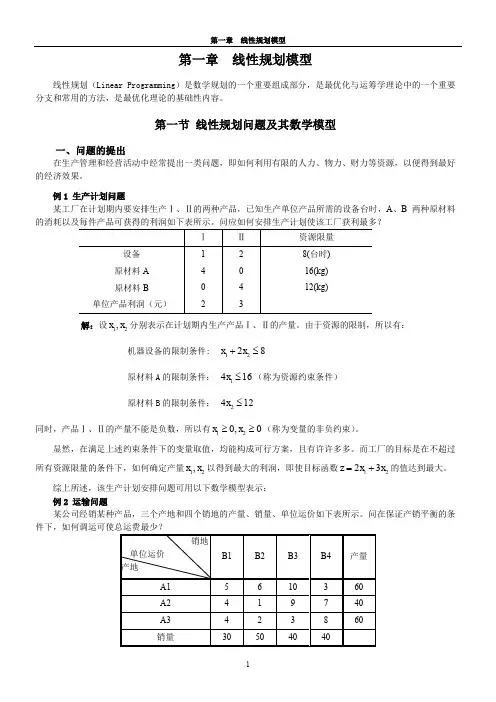
例1 生产计划问题某工厂在计划期内要安排生产Ⅰ、Ⅱ的两种产品,已知生产单位产品所需的设备台时,A 、B 两种原材料的消耗以及每件产品可获得的利润如下表所示。
问应如何安排生产计划使该工厂获利最多?解:设12,x x 分别表示在计划期内生产产品Ⅰ、Ⅱ的产量。
由于资源的限制,所以有:机器设备的限制条件: 1228x x +≤原材料A 的限制条件: 1416x ≤(称为资源约束条件) 原材料B 的限制条件: 2412x ≤同时,产品Ⅰ、Ⅱ的产量不能是负数,所以有120,0x x ≥≥(称为变量的非负约束)。
显然,在满足上述约束条件下的变量取值,均能构成可行方案,且有许许多多。
而工厂的目标是在不超过所有资源限量的条件下,如何确定产量12,x x 以得到最大的利润,即使目标函数1223z x x =+的值达到最大。
综上所述,该生产计划安排问题可用以下数学模型表示:例2 运输问题某公司经销某种产品,三个产地和四个销地的产量、销量、单位运价如下表所示。
问在保证产销平衡的条解:(1)决策变量:设(1,2,3;1,2,3,4)ij x i j ==为从产地i 运到销地j 的运量(2)目标函数:总运费最小3411min ij iji j z c x===∑∑(3)约束条件: 产量约束 销量约束 非负约束 模型为:二、线性规划问题的模型上述几例所提出的问题,可归结为在变量满足线性约束条件下,求使线性目标函数值最大或最小的问题。
它们具有以下共同的特征。
(1)每个问题都可用一组决策变量12(,,,)n x x x 表示某一方案,其具体的值就代表一个具体方案。





1、图解法适用于含有()个变量的线性规划问题。
正确答案:两或22、线性规划问题的可行解是指满足()的解。
正确答案:所有约束条件3、在线性规划问题的基本解中,所有的非基变量等于()。
正确答案:零或04、若线性规划问题有最优解,则最优解一定可以在可行域的()达到。
正确答案:顶点或极点5、线性规划问题有可行解,则必有()。
正确答案:基可行解6、如果线性规划问题存在目标函数为有限值的最优解,求解时只需在其()的集合中进行搜索即可得到最优解。
正确答案:基可行解7、满足()条件的基本解称为基本可行解。
正确答案:非负8、求解线性规划问题可能的结果有四种,分别是()。
正确答案:无解,有唯一最优解,有无穷多个最优解和退化解9、求一个线性函数在一组()约束条件下的最大化或最小化问题,称为线性规划问题。
正确答案:线性1、若x、y满足约束条件{x≤2 y≤2x+y≥2则z=x+2y的取值范围是()。
A. [2,6]B. [2,5]C. [3,6]D. [3,5]正确答案:A2、为化为标准形式而引入的松弛变量在目标函数中的系数应为()。
A.0B.1C.2D.3正确答案:A3、若线性规划问题没有可行解,可行解集是空集,则此问题()。
A.没有无穷多最优解B.没有最优解C.有无界解D.没有无界解正确答案:B4、在单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个解中()。
A.不影响解的可行性B.至少有一个基变量的值为负C.找不到出基变量D.找不到进基变量正确答案:B5、用单纯形法求解极大化线性规划问题中,若某非基变量检验数为零,而其他非基变量检验数全部<0,则说明本问题()。
A.有惟一最优解B.有多重最优解C.无界D.无解正确答案:B6、单纯形法当中,入基变量的确定应选择检验数()。
A.绝对值最大B.绝对值最小C.正值最大D.负值最小正确答案:C7、在单纯形表的终表中,若非基变量的检验数有0,那么最优解()。
A.不存在B.唯一C.无穷多D.无穷大正确答案:A8、线性规划模型不包括下列()要素。