沪教版高中数学教材梳理

沪教版高三数学知识点数学是一门精密而又抽象的学科，对于高中生来说，数学知识点的理解和掌握尤为重要。

而沪教版高三数学知识点的学习内容极其丰富而充实，下面我们就来一起探讨一些重要的数学知识点。

一、函数与方程函数与方程是高三数学中最基础、最重要的概念之一。

函数是自变量和因变量之间的一种对应关系，常见的函数有线性函数、平方函数、三次函数等等。

方程则是等式的一种特殊形式，根据方程的类型可以使用不同的方法进行求解，比如线性方程组可以用消元法，二次方程可以用配方法。

二、数列与数列极限数列是数学中有限个数按一定顺序排列成的序列，它是数学中研究一切数量变化规律的基本工具。

数列中最重要的是数列的极限，即数列当n趋于无穷大时的极限值。

通过研究数列的极限可以得到数列的性质和趋势，使我们能够更好地理解数学中的变化规律。

三、导数与微分导数是数学中极为重要的概念，其可用于描述函数的变化率，进而求解函数的最值问题。

微分则是导数所属的一种运算方法，利用微分可以求解函数的极值和函数图像的性质。

导数与微分不仅在高中数学学习中起着重要作用，更是在大学数学和相关科学领域中使用最广泛的数学工具。

四、立体几何与空间向量在几何学的学习中，立体几何是数学中一门重要的分支。

立体几何研究的是三维空间中的图形和其性质。

通过学习立体几何，我们可以了解到各类多面体的性质，掌握空间图形的投影和相似性质。

此外，空间向量也是立体几何中的重要内容，它是空间中向量的推广，可用于解决直线和平面的位置关系问题。

五、概率与统计概率与统计是现代数学中的新兴学科，其独特的方法与思维方式对于我们解决各类实际问题具有重要的指导意义。

学习概率与统计可以使我们更好地理解概率的概念和应用，掌握统计数据的分析和处理方法。

在日常生活中，概率与统计也是我们进行决策和判断的基础。

六、三角函数和平面向量三角函数是高中数学中非常重要的知识点，它们是数学中研究角度与边长关系的基本工具。

三角函数的性质和应用不仅在数学学科中有广泛的应用，更是在物理、工程等学科中也有着重要地位。

高中数学知识点归纳高一（上）数学知识点归纳第一章 集合与命题1.主要内容：集合的基本概念、空集、子集和真子集、集合的相等；集合的交、 并、补运算。

四种命题形式、等价命题;充分条件与必要条件.2.基本要求：理解集合、空集的意义，会用列举法和描述法表示集合；理解子集、真子集、集合相等等概念，能判断两个集合之间的包含关系或相等关系；理解交集、并集，掌握集合的交并运算，知道有关的基本运算性质，理解全集的意义,能求出已知集合的补集.理解四种命题的形式及其相互关系，能写出一个简单命题的逆命题、否命题与逆否命题；理解充分条件、必要条件与充要条件的意义,能在简单问题的情景中判断条件的充分性、必要性或充分必要性。

3.重难点：重点是集合的概念及其运算，充分条件、必要条件、充要条件。

难点是对集合有关的理解，命题的证明,充分条件、必要条件、充要条件的判别。

4.集合之间的关系：(1)子集：如果A 中任何一个元素都属于B ，那么A 是B 的子集,记作A ⊆B.(2）相等的集合：如果A ⊆B,且B ⊆A,那么A=B 。

(3).真子集：A ⊆B 且B 中至少有一个元素不属于A,记作A ⊆B 。

5.集合的运算：(1）交集：}.{B x A x x B A ∈∈=且(2）并集：}.{B x A x x B A ∈∈=或 （3）补集：}.{A x U x x A C U ∉∈=且6。

充分条件、必要条件、充要条件如果P Q ⇒,那么P 是Q 的充分条件,Q 是P 的必要条件。

如果P Q ⇔,那么P 是Q 的充要条件。

也就是说,命题P 与命题Q 是等价命题。

有关概念：1。

我们把能够确切指定的一些对象组成的整体叫做集合。

2.数集有：自然数集N ，整数集Z ，有理数集Q ,实数集R .3。

集合的表示方法有列举法、描述法和图示法.4。

用平面区域来表示集合之间关系的方法叫做集合的图示法,所用图叫做文氏图。

5.真子集，交集，并集，全集,补集。

6.命题，逆命题，否命题，逆否命题，等价命题。

目录一、集合与常用逻辑二、不等式三、函数概念与性质四、基本初等函数五、函数图像与方程六、三角函数七、数列八、平面向量九、复数与推理证明十、直线与圆十一、曲线方程十二、矩阵、行列式、算法初步十三、立体几何十四、计数原理十五、概率与统计一、集合与常用逻辑1．集合概念元素：互异性、无序性2．集合运算全集U ：如U=R交集：}{B x A x x B A 且并集：}{B xA xx BA或补集：}{A xU xx A C U 且3．集合关系空集A 子集B A :任意Bx AxBABBABAAB A 注：数形结合---文氏图、数轴4．四种命题原命题：若p 则q 逆命题：若q 则p否命题：若p 则q逆否命题：若q 则p原命题逆否命题否命题逆命题5．充分必要条件p 是q 的充分条件：q P p 是q 的必要条件：qPp 是q 的充要条件：p?q 6．复合命题的真值①q 真（假）?“q ”假（真）②p 、q 同真?“p ∧q ”真③p 、q 都假?“p ∨q ”假7.全称命题、存在性命题的否定M, p(x ）否定为: M, )(X p M, p(x ）否定为:M,)(X p二、不等式1．一元二次不等式解法若0a，02cbx ax有两实根,)(，则02c bx ax 解集),(02cbxax解集),(),(注：若0a ，转化为0a情况2．其它不等式解法—转化ax aa x 22axaxa x或ax22ax)()(x g x f 0)()(x g x f )()(x g x f aa)()(x g x f （a 1）)(log )(log x g x f a a f x f x g x ()()()0（01a ）3．基本不等式①ab b a222②若R ba,，则ab ba 2注：用均值不等式ab b a2、2)2(b a ab求最值条件是“一正二定三相等”三、函数概念与性质1．奇偶性f(x)偶函数()()f x f x f(x)图象关于y 轴对称f(x)奇函数()()f x f x f(x)图象关于原点对称注：①f(x)有奇偶性定义域关于原点对称②f(x)奇函数,在x=0有定义f(0)=0③“奇+奇=奇”（公共定义域内）2．单调性f(x)增函数：x 1＜x 2f(x 1)＜f(x 2) 或x 1＞x 2f(x 1) ＞f(x 2)或)()(2121x x x f x f f(x)减函数：？注：①判断单调性必须考虑定义域②f(x)单调性判断定义法、图象法、性质法“增+增=增”③奇函数在对称区间上单调性相同偶函数在对称区间上单调性相反3．周期性T 是()f x 周期()()f x T f x 恒成立（常数0T ）4．二次函数解析式： f(x)=ax 2+bx+c ，f(x)=a(x-h)2+kf(x)=a(x-x1)(x-x2)对称轴：a b x2顶点：)44,2(2abacab 单调性：a>0，]2,(ab递减，),2[ab 递增当abx2，f(x)minabac442奇偶性：f(x)=ax 2+bx+c 是偶函数b=0闭区间上最值：配方法、图象法、讨论法---注意对称轴与区间的位置关系注：一次函数f(x)=ax+b奇函数b=0四、基本初等函数1．指数式)0(10aannaa 1mnmnaa2．对数式bN a log N ab（a>0,a ≠1）NM MN a a a log log log NM N M a a alog log log Mn M a na log log ab bm m a log log log ab lg lg naa b bnl o g l o g a b l o g 1注：性质1log a 1log aa NaNa log 常用对数N N 10log lg ，15lg 2lg 自然对数N N e log ln ，1ln e 3．指数与对数函数y=a x与y=log a x定义域、值域、过定点、单调性？注：y=a x与y=log a x 图象关于y=x 对称（互为反函数）4．幂函数12132,,,xyx yx yx y x y在第一象限图象如下：1010五、函数图像与方程1．描点法函数化简→定义域→讨论性质（奇偶、单调）取特殊点如零点、最值点等2．图象变换平移：“左加右减，上正下负”)()(h x f y x f y伸缩：)1()(x f y x f y 倍来的每一点的横坐标变为原对称：“对称谁，谁不变，对称原点都要变”)()()()()()(x f yx f y x f y x f y x f y x f y y x 原点轴轴注：)(x f yax直线)2(x af y翻折：)(x f y |()|y f x 保留x 轴上方部分，并将下方部分沿x 轴翻折到上方y=f(x)cbaoyxy=|f(x)|cb aoyx)(x f y (||)y f x 保留y 轴右边部分，并将右边部分沿y 轴翻折到左边y=f(x)cb aoyxy=f(|x|)cb aoyx3．零点定理若0)()(b f a f ，则)(x f y 在),(b a 内有零点（条件：)(x f 在],[b a 上图象连续不间断）注：①)(x f 零点：0)(x f 的实根②在],[b a 上连续的单调函数)(x f ，0)()(b f a f 则)(x f 在),(b a 上有且仅有一个零点③二分法判断函数零点---0)()(b f a f ？六、三角函数1．概念第二象限角)2,22(kk(Z k )2．弧长r l 扇形面积lrS213．定义ry sinrx cosx y tan其中),(y x P 是终边上一点，rPO4．符号“一正全、二正弦、三正切、四余弦”5．诱导公式：“奇变偶不变，符号看象限”如sin)2(Sin ，sin)2/cos(6．特殊角的三角函数值643223sin 0212223 11cos 1 23222101tg33 13/ 0 /7．基本公式同角1cossin 22tancossin 和差sincos cossin sinsinsincos cos cos tantan1tan tan tan倍角cos sin 22sin 2222sin211cos2sincos2cos 2tan1tan 22tan 降幂cos 2α=22cos 1 sin2α=22cos 1叠加)4sin(2cossin )6sin(2cossin3)sin(cos sin 22b ab a )(tanba 8．三角函数的图象性质单调性：)2,2(增),0(减)2,2(增注：Zk y=sinxy=cosxy=tanx图象sinxcosx tanx 值域[-1，1] [-1，1] 无奇偶奇函数偶函数奇函数周期2π2ππ对称轴2/kx kx 无中心,k0,2/k 0,2/k9．解三角形基本关系：sin(A+B)=sinCcos(A+B)=-cosCtan(A+B)=-tanC2cos2sinC BA 正弦定理：Aa sin =Bb sin =Ccsin AR a sin 2CB A cb a s i n :s i n :s i n ::余弦定理：a 2=b 2+c 2－2bccosA （求边）cosA=bcac b 2222（求角）面积公式：S △＝21absinC注：ABC 中，A+B+C=？BABAsin sin a 2＞b 2+c 2∠A ＞2七、数列1、等差数列定义：d a a n n 1通项：dn a a n )1(1求和：2)(1n na a n S dn n na )1(211中项：2ca b （c b a ,,成等差）性质：若q p n m ，则qp n ma a a a 2、等比数列定义：)0(1q q a a nn 通项：11n n qa a 求和：)1(1)1()1(11qqq a qna S nn中项：ac b 2（c b a ,,成等比）性质：若qpnm则qp nm a a a a 3、数列通项与前n 项和的关系)2()1(111ns s n a s a nnn4、数列求和常用方法公式法、裂项法、错位相减法、倒序相加法八、平面向量1．向量加减三角形法则，平行四边形法则BCABAC首尾相接，OC OB =CB 共始点中点公式：AD ACAB 2D 是BC 中点2．向量数量积b a =cosba=2121y y x x 注：①b a ,夹角：00≤θ≤180②b a,同向：ba ba 3．基本定理2211e ea（21,e e 不共线--基底）平行：b a //ba 1221y x y x （0b ）垂直：0b a ba 02121y y x x 模：a ＝22yx 22)(b a b a 夹角：cos||||b a b a 注：①0∥a②c b a cb a（结合律）不成立③ca ba c b（消去律）不成立九、复数与推理证明1．复数概念复数：bi a z (a,b )R ，实部a 、虚部 b分类：实数（0b），虚数（0b ），复数集 C 注：z 是纯虚数0a ，0b 相等：实、虚部分别相等共轭：bia z模：22baz 2zz z 复平面：复数z 对应的点),(b a 2．复数运算加减：（a+bi ）±(c+di)=？乘法：（a+bi ）（c+di ）=？除法：di c bi a =))(())((di cdi cdi c bi a ==…乘方：12i ，ni rrk i i 43．合情推理类比：特殊推出特殊归纳：特殊推出一般演绎：一般导出特殊（大前题→小前题→结论）4．直接与间接证明综合法：由因导果比较法：作差—变形—判断—结论反证法：反设—推理—矛盾—结论分析法：执果索因分析法书写格式：要证A 为真，只要证B 为真，即证……，这只要证C 为真，而已知C 为真，故A 必为真注：常用分析法探索证明途径，综合法写证明过程5．数学归纳法：(1)验证当n=1时命题成立,(2)假设当n=k(kN* ，k 1)时命题成立,证明当n=k+1时命题也成立由(1)(2)知这命题对所有正整数n 都成立注：用数学归纳法证题时，两步缺一不可，归纳假设必须使用十、直线与圆1、倾斜角范围0,斜率2121tany y k x x 注：直线向上方向与x 轴正方向所成的最小正角倾斜角为90时，斜率不存在2、直线方程点斜式)(00x x k y y ，斜截式b kx y 两点式121121x x x x y y y y ，截距式1by ax 一般式0CByAx注意适用范围：①不含直线0xx ②不含垂直x 轴的直线③不含垂直坐标轴和过原点的直线3、位置关系（注意条件）平行12k k 且21b b 垂直121k k 垂直1212A AB B 4、距离公式两点间距离：|AB|=221221)()(y y x x 点到直线距离：0022Ax By CdAB5、圆标准方程：222)()(rb y a x圆心),(b a ，半径r圆一般方程：022FEy Dx yx（条件是？）圆心,22D E 半径2242DE Fr6、直线与圆位置关系注：点与圆位置关系222)()(rb y a x 点00,P x y 在圆外7、直线截圆所得弦长222AB rd十一、圆锥曲线一、定义椭圆： |PF1|+|PF 2|=2a(2a>|F1F 2|)双曲线：|PF 1|-|PF 2|=±2a(0<2a<|F 1F 2|) 抛物线：与定点和定直线距离相等的点轨迹二、标准方程与几何性质（如焦点在x 轴）位置关系相切相交相离几何特征d rd rd r代数特征△0△0△椭圆12222by ax ( a>b>0)双曲线12222by ax (a>0,b>0)中心原点对称轴？焦点F 1(c,0)、F 2(-c,0)顶点:椭圆(±a,0),(0, ±b)，双曲线(±a,0) 范围: 椭圆-a x a,-by b双曲线|x|a ，y R焦距：椭圆2c （c=22b a）双曲线2c （c=22b a ）2a 、2b:椭圆长轴、短轴长，双曲线实轴、虚轴长离心率：e=c/a 椭圆0<e<1,双曲线e>1注：双曲线12222b y ax 渐近线x a b y 方程122ny mx 表示椭圆nmnm.0,0方程122nymx表示双曲线mn 抛物线y 2=2px(p>0)顶点（原点）对称轴（x 轴）开口（向右）范围x 0 离心率e=1焦点)0,2(p F 准线2p x十二、矩阵、行列式、算法初步十、算法初步一．程序框图二．基本算法语句及格式1输入语句：INPUT “提示内容”；变量2输出语句：PRINT “提示内容”；表达式3赋值语句：变量=表达式4条件语句“IF —THEN —ELSE ”语句“IF —THEN ”语句程序框名称功能起止框起始和结束输入、输出框输入和输出的信息处理框赋值、计算判断框判断某一条件是否成立循环框重复操作以及运算IF 条件 THEN IF条件 THEN 语句1 语句ELSE END IF语句2 END IF 5循环语句当型循环语句直到型循环语句WHILE 条件 DO 循环体循环体WEND LOOP UNTIL 条件当型“先判断后循环”直到型“先循环后判断”三．算法案例1、求两个数的最大公约数辗转相除法：到达余数为更相减损术：到达减数和差相等2、多项式f(x)= a n x n+a n-1xn-1+….+a 1x+a 0的求值秦九韶算法：v 1=a n x+a n －1v 2=v 1x+a n －2 v 3=v 2x+a n －3v n =v n －1x+a 0注：递推公式v 0=a n v k =v k －1X +a n －k (k=1,2,…n)求f(x)值，乘法、加法均最多n 次3、进位制间的转换k 进制数转换为十进制数：111011.........)(.....a ka ka ka k a a a a n nnnn n 十进制数转换成k 进制数：“除k 取余法”例1辗转相除法求得123和48最大公约数为3例2已知f(x)=2x5－5x 4－4x 3+3x 2－6x+7，秦九韶算法求f(5)123＝2×48＋27 v 0=248＝1×27＋21 v 1=2×5－5=527＝1×21＋6 v 2=5×5－4=2121＝3×6＋3 v3=21×5+3=108 6＝2×３+0 v4=108×5－6=534v 5=534×5+7=2677十三、立体几何1．三视图正视图、侧视图、俯视图2．直观图：斜二测画法'''X OY =45平行X 轴的线段，保平行和长度平行Y 轴的线段，保平行，长度变原来一半3．体积与侧面积V 柱=S 底h V锥 =31S 底h V球=34πR3S 圆锥侧=rlS圆台侧=lr R )( S球表=24R4．公理与推论确定一个平面的条件：①不共线的三点②一条直线和这直线外一点③两相交直线④两平行直线公理：平行于同一条直线的两条直线平行定理：如果两个角的两条边分别对应平行，那么这两个角相等或互补。

沪教版高三数学知识点总结数学，作为一门学科，无论在高中阶段还是大学阶段，都是学生比较苦恼的一门科目。

数学需要一定的逻辑思维和计算能力，而在高三阶段，往往是学生最为关注的时期，所以在这个时候，对于数学知识点的掌握显得尤为重要。

在沪教版的数学课程中，高三数学知识点可以分为几大模块，下面我将对这些模块逐一进行总结。

第一部分：抽象代数与数与式在高三数学中，代数是相对来说比较基础的一个模块，它涉及到代数式的展开和因式分解，方程与不等式的解法等内容。

对于代数式的展开，主要是通过乘法公式和整式乘法的方法，将复杂的代数式转化为简单的形式。

而对于因式分解，可以采用公因式提取法、提公因式法、公式法等方法，将复杂的代数式分解为简单的因式。

第二部分：函数与方程函数与方程是高三数学中的重点内容，也是最为基础的数学知识。

在函数与方程的学习中，我们需要掌握函数的概念、性质和常见函数的图像特征。

其中，二次函数的图像特征是比较重要的一部分，我们需要了解二次函数的开口方向、顶点坐标和对称轴等相关知识点。

在方程与不等式的解法中，我们需要熟悉一元二次方程的求解方法，了解一次不等式和二次不等式的解集表示方法。

除此之外，我们还需要掌握绝对值方程和绝对值不等式的性质和解法。

第三部分：立体几何与解析几何立体几何与解析几何是高三数学中相对较难的一个模块，它涉及到三维空间中点、线、面的位置关系，也包括了平面几何的内容。

在立体几何的学习中，我们需要了解空间中点、线、面的投影和距离的计算方法，掌握平面与立体图形的求交性质和相关的空间几何题型。

解析几何是数学与几何的结合，它以坐标系为基础，通过代数的方法研究几何问题。

在解析几何的学习中，我们需要了解直线与圆的方程表示方法，掌握直线与圆的位置关系和相交性质。

同时，我们还需要掌握向量的基本运算规律和性质，了解向量与直线的位置关系和向量与平面的垂直、平行关系。

第四部分：概率与统计概率与统计是高三数学中较为实用的一个模块，它涉及到实际问题中的概率计算和数据处理。

目录一、集合与常用逻辑 二、不等式 三、函数概念与性质 四、基本初等函数 五、函数图像与方程 六、三角函数 七、数 列 八、平面向量九、复数与推理证明 十、直线与圆 十一、曲线方程 十二、矩阵、行列式、算法初步 十三、立体几何 十四、计数原理 十五、概率与统计 补集： C U A {xx U 且x A}3．集合关系空集A子集 A B : 任意x A x B注：数形结合 --- 文氏图、数轴4．四种命题原命题：若 p 则q否命题：若 p 则 q原命题 逆否命题5．充分必要条件p 是 q 的充分条件： P q p是 q 的必要条件： P q p 是 q的充要条件： p? q 6．复合命题的真值① q 真(假) ? “ q ”假(真) ② p 、q 同真 ? “ p ∧ q ”真③ p 、q 都假 ? “ p ∨ q ”假7. 全称命题、存在性命题的否定M, p(x )否定为 : M, p(X) M, p(x )否定为 : M, p(X)并集： A B {x x A 或 x B}一、集合与常用逻辑1．集合概念 元素：互异性、无序性 2．集合运算全集 U ：如 U=R交集： A B {x x A 且x B}逆命题：若 q 则p逆否命题：若 q 则 p 否命题 逆命题二、不等式1．一元二次不等式解法若a 0，ax2 bx c 0有两实根, ( ) ，则ax2 bx c0 解集( , ) ax2 bx c 0 解集( , ) ( , ) 注：若a 0，转化为a 0 情况2．其它不等式解法—转化x a a x a x2 a2x a x a 或x a x2 a2f(x)0 f (x)g(x) 0g(x)a f(x)ag(x)f (x) g(x)( a 1)f (x) 0log a f(x) log a g(x) (0 a 1)a a f (x) g(x)3．基本不等式①a2 b 2 2ab②若a,b R ，则 a b ab2注：用均值不等式a b 2 ab 、ab (a b)22 求最值条件是“一正二定三相等”三、函数概念与性质1．奇偶性f(x) 偶函数 f ( x) f (x) f(x) 图象关于y 轴对称f(x) 奇函数 f ( x) f(x) f(x) 图象关于原点对称注：① f(x) 有奇偶性定义域关于原点对称② f(x) 奇函数, 在x=0 有定义f(0)=0③“奇+奇=奇”(公共定义域内)2．单调性f(x) 增函数：x1<x2 f(x 1) <f(x 2)或x1> x2 f(x 1) > f(x 2)或f (x1) f (x2)x1 x2f(x) 减函数：？注：①判断单调性必须考虑定义域② f(x) 单调性判断定义法、图象法、性质法“增+增=增”③奇函数在对称区间上单调性相同偶函数在对称区间上单调性相反3．周期性T是f(x)周期f(x T) f (x)恒成立(常数T 0) 4．二次函数解析式：f(x)=ax 2+bx+c，f(x)=a(x-h) 2+kf(x)=a(x-x 1)(x-x 2)对称轴：b x2a顶点：b 4 ac b 2 (2a, )4a单调性：a>0， (2b a] 递减， [ 2ba ,) 递增4ac b 2b当 x， f(x) min2a4 af(x)=ax 2+bx+c 是偶函数 b=0闭区间上最值： l og a b log nb n 1a alog b a注：性质 log a 1 0 log a a 1 a loga N N 常用对数 lg N log 10 N ， lg2 lg 5 1 自然对数 ln N log e N ， lne 13．指数与对数函数y=a x 与 y=log a xlog aN奇偶性：配方法、图象法、讨论法 -- 注意对称轴与区间的位置关系 注：一次函数f(x)=ax+b 奇函数 b=0 四、基本初等函数 1．指数式 2．对数式 n n 1m m n1 (a 0) a n a ma a log a Nb a b N ( a>0,a ≠1)log a MN log a M log a N M log a log a M log a N N log aM nnlog a M log m b lgb log a b log m a lga a 0定义域、值域、过定点、单调性？注： y=a x与 y=log a x 图象关于 y=x 对称（互为反函数）14．幂函数y x 2,y x 3, y x 2, y x 1y x 在第一象限图象如下：五、函数图像与方程1．描点法函数化简→定义域→讨论性质(奇偶、单调) 取特殊点如零点、最值点等2．图象变换平移：“左加右减，上正下负”y f (x) y f (x h)伸缩：y f (x)每一点的横坐标变为原来的倍y f (1x)对称：“对称谁，谁不变，对称原点都要变”y f(x) x轴y f(x)y f(x) y 轴y f( x)y f(x) 原点y f( x)直线x a注：y f (x) y f (2a x)翻折：y f (x) y | f (x)|保留x轴上方部分，并将下方部分沿x 轴翻折到上方y f (x) y f (| x |)保留y 轴右边部分，并将右边部分沿y 轴翻折到左边yy=f(x)yy=f(|x|)ao b c x a o bc 3．零点定理若f(a)f (b) 0，则y f(x)在(a,b)内有零点(条件：f (x) 在［a,b］上图象连续不间断)注：① f (x) 零点：f(x) 0 的实根②在［a, b］上连续的单调函数 f(x)f (a)f(b)0 则f(x) 在(a,b) 上有且仅有一③二分法判断函数零点--- f(a) f (b) 0？六、三角函数1．概念第二象限角(2k ,2k ) ( k Z )2．弧长l r扇形面积S1lr23．定义sin y xcos tan yr r x其中P(x,y)是终边上一点，PO r4．符号“一正全、二正弦、三正切、四余弦”5．诱导公式：“奇变偶不变，符号看象限”如Sin(2 ) sin ，cos( /2 ) sin6．特殊角的三角函数值6 4 3 23 2sin 01 2 2 2 3 2 11 cos1 32 2 21 2 010 tg 0 3 313//2 2aasin bcos a 2 b 2sin() (tan )b7．基本公式 sin tan cos 和差 sin sin cos cos sin同角 sin 2 cos 21cos cos cos sin sintan tantan1 tan tan 倍角 sin2 2sin cos2 2 2 2cos2 cos sin 2cos 1 1 2sintan22tan21 tan 2降幂2 1 cos2cos α =2si n21 cos2α=sinxcosx tanx值域 [-1 ， 1][-1 ， 1]无 奇偶 奇函数偶函数奇函数周期 2π 2π π对称轴x k / 2xk无中心k ,0/ 2 k ,0k /2,0叠加 sin cos 2sin( )注： k Z3sin cos 2sin( )9．解三角形2、等比数列A B Ctan(A+B)=-tanC sin cos221面积公式：S△＝absinC2七、数列1、等差数列定义：a n 1 a n d通项：a n a1(n 1)d求和：Sn n(a1 a n)na11n(n 1)d22ac中项：b ( a,b,c成等差)2性质：若m n p q ，则a m a n a p a q基本关系sin(A+B)=sinC cos(A+B)=-cosC定义：an 1q(q 0) a n注：ABC 中，A+B+C=？A B sinA sinBa2>b2+c2? ∠A >24、数列求和常用方法公式法、裂项法、错位相减法、倒序相加法通项：a n a1q n 1正弦定理sin A sin B sinC求和：S na 2RsinA a:b:c sinA:sinB:sinC余弦定理：a2=b2+c2－2bccosA(求边)cosA=2222中项：na1 (q 1)a1(11q qn)(q 1)1qac( a,b,c 成等比)则a m a n a p a qb2若m n p q2bc求角）3、数列通项与前 n 项和的关系s1a1(n 1) s ns n 1(n 2)a n9．解三角形2、等比数列八、平面向量1．向量加减三角形法则，平行四边形法则AB BC AC 首尾相接，OB OC =CB 共始点中点公式：AB AC 2AD D 是BC中点a b cos2．向量数量积a b= =x1x2 y1 y2注：① a ,b 夹角：00≤ θ ≤ 1800② a,b同向：a b a b3．基本定理a 1e1 2e2（e1,e2不共线-- 基底）模：z a2 b2z z z复平面：复数z 对应的点（a,b）2．复数运算平行：a//b a b x1y2 x2y1( b 0 )垂直：a b a b 0 x1x2 y1y2 0夹角：cos a b|a||b|注：① 0∥ a ② a b c a b c （结合律）不成立③ a b a c b c （消去律）不成立加减：（a+bi ）± （c+di）= ？乘法：（a+bi ）（c+di ）=？a bi=(a bi)(c di)c di (c di)(c di)乘方：i21，i n i4k r i r3．合情推理类比：特殊推出特殊归纳：特殊推出一般演绎：一般导出特殊（大前题→小前题→结论）4．直接与间接证明综合法：由因导果比较法：作差—变形—判断—结论反证法：反设—推理—矛盾—结论分析法：执果索因九、复数与推理证明1．复数概念复数：z a bi （a,b R），实部a、虚部b 分类：实数（b 0 ），虚数（b 0），复数集C注：z 是纯虚数a 0 ，b 0相等：实、虚部分别相等共轭：z a bi分析法书写格式：要证A 为真，只要证B为真，即证⋯⋯，这只要证C为真，而已知C为真，故A 必为真注：常用分析法探索证明途径，综合法写证明过程5．数学归纳法：（1）验证当n=1 时命题成立,（2）假设当n=k（k N* ，k 1）时命题成2(a b) 2除法：由（1）（2）知这命题对所有正整数n 都成立注：用数学归纳法证题时，两步缺一不可，归纳假设必须使用模：立证明当n=k+1 时命题也成立十、直线与圆1、倾斜角范围0,斜率k tan y2 y1x2 x1注：直线向上方向与x轴正方向所成的最小正角倾斜角为90 时，斜率不存在2、直线方程点斜式y y0 k(x x0)，斜截式y kx b两点式y y1 x x1 ，截距式x y 1y2 y1 x2 x1 a b一般式Ax By C 0 注意适用范围：①不含直线x x0②不含垂直x 轴的直线③不含垂直坐标轴和过原点的直线3、位置关系 (注意条件) 平行k1 k2 且b1 b2垂直k1k2 1 垂直A1A2 B1B2 04、距离公式两点间距离：|AB|= (x1x2)2(y1y2)2点到直线距离： d AxByCA2B25、圆标准方程：(x a)2 (y b)2 r2圆心( a , b ) ，半径r圆一般方程：x2 y2 Dx Ey F 0(条件是？)6、直线与圆位置关系注：点与圆位置关系(x0 a)2 (y0 b)2 r2点P x0,y0在圆外7、直线截圆所得弦长AB 2 r 2d2一、圆锥曲线、定义椭圆：|PF 1|+|PF 2|=2a(2a>|F 1F2|)双曲线：|PF 1|-|PF 2|= ± 2a(0<2a<|F1F2|) 抛物线：与定点和定直线距离相等的点轨迹、标准方程与几何性质 (如焦点在x轴)圆心D2 E 半径r D2 E2 4F2222椭圆x2y2 1( a>b>0)a 2b2 22双曲线x2y2 1(a>0,b>0)a 2b2中心原点对称轴？焦点F1(c,0) 、F2(-c,0) 顶点: 椭圆( ± a,0),(0, ±b) ，双曲线(±a,0) 范围: 椭圆-a x a,-b y b双曲线|x| a ，y R焦距：椭圆2c (c= a2b2)双曲线2c( c= a2b2)2a、2b: 椭圆长轴、短轴长，双曲线实轴、虚轴长离心率：e=c/a 椭圆0<e<1, 双曲线e>1x 2y2注：双曲线x2y2 1 渐近线y b xa 2b2a十二、矩阵、行列式、算法初步十、算法初步22方程mx ny 1表示椭圆m 0,n 0.m n22方程mx2 ny2 1 表示双曲线mn 0 抛物线y2=2px(p>0)顶点(原点) 对称轴( x 轴)开口(向右) 范围x 0 离心率e=1焦点F( p,0)2 准线x p2．程序框．基本算法语句及格式1输入语句：INPUT “提示内容” ；变量2输出语句：PRINT“提示内容” ；表达式3赋值语句：变量=表达式4条件语句IF —THEN—ELSE”语句“IF —THEN”语句IF 条件 THEN 语句 1IF条件 THEN 语句ELSEEND IF语句 2END IF5 循环语句当型循环语句直到型循环语句WHILE 条件DO循环体循环体WENDLOOP UNTIL 条件当型“先判断后循环” 直到型“先循环后判断” 例 1 辗转相除法求得 123 和 48 最大公约数为 3例 2 已知 f(x)=2x 5－5x 4－ 4x 3+3x 2－6x+7，秦九韶算法求 f(5)123＝2×48＋ 27 v 0=248＝1×27＋ 21 v 1=2× 5－ 5=527 ＝ 1× 21＋ 6v2=5× 5－ 4=2121＝3× 6＋3 v 3=21× 5+3=1086＝ 2×3+0v4=108×5－6=534v 5=534×5+7=2677三．算法案例1、求两个数的最大公约数 辗转相除法：到达余数为0 更相减损术：到达减数和差相等2、多项式 f(x)= a n x n+a n-1x n-1+⋯.+a 1x+a 0 的求值十三、立体几何2S 圆锥侧 = rl S 圆台侧 = (R r)l S 球表 =4 R 24． 公理与推论 确定一个平面的条件 ：①不共线的三点 ②一条直线和这直线外一点十进制数转换成 k 进制数：“除 k 取余法秦九韶算法 ：v 1=a n x+a n －1 v 2=v 1x+an －2v 3=v 2x+a n v n =v n －1x+a 0注：递推公式 v 0=an vk=v k －1X +a n －k (k=1,2, ⋯ n) 求 f(x) 值，乘法、加法均最多n 次3、进位制间的转换k 进制数转换为十进制数：a n a n 1 ... a 1a 0(k) a n k n a n 1 k n 1 ..... a 1 k a 02．直观图 ：斜二测 画法 X 'OY ' '=450 平行 X轴的线段，保平行和长度平行 轴 的线段，保平长度变原来一半3．体积与侧面积1V 柱 =S 底 h V 锥 = S 底 h3V43 球= π R 31． 三视图 正视图、侧视图、俯视图若两个平面垂直，则一个平面内垂直于交公理 ：平行于同一条直线的两条直线平行定理 ：如果两个角的两条边分别对应平行，那么这两个角相等或互补。

沪教版高一数学知识点归纳整理数学作为一门学科，是我们日常生活中无处不在的。

它不仅在工作和学习中发挥着重要的作用，还在我们解决问题和做决策时提供了有效的工具和思维方式。

而在高一阶段，学生们将进一步深入学习数学的各个领域，为后续的学习打下坚实的基础。

在沪教版的数学教材中，有一些重要的知识点需要我们掌握和理解。

本文将对这些知识点进行归纳整理。

一、函数与方程函数与方程是数学中的两个基本概念，也是高一数学的重点内容之一。

在函数的学习中，我们不仅需要了解函数的定义和性质，还需要学会用函数来解决实际问题。

方程则是用来表示两个量之间的关系的等式，通过解方程可以求得未知数的值。

在高一数学中，我们将学习到一元一次方程和一元二次方程的解法，以及一些特殊方程的解法。

二、平面向量平面向量是数学中的一种重要工具，它可以表示空间中的运动和力的大小和方向。

在高一数学中，我们将学习如何表示和运算平面向量，并且掌握向量空间和向量的线性相关性质。

此外，我们还将学习到平面向量的数量积和向量积，以及它们在几何问题中的应用。

三、三角函数三角函数是数学中的一门重要分支，它研究的是角度和三角形之间的关系。

在高一数学中，我们将学习到正弦函数、余弦函数和正切函数的定义和性质。

此外，我们还要学习如何利用三角函数解决实际问题，比如三角恒等式和解三角形等。

四、立体几何立体几何是数学中的一门重要分支，它研究的是空间中的点、直线和面的关系。

在高一数学中，我们将学习到立体几何的基本概念，比如点、直线、平面和空间等。

此外，我们还要学习到立体几何的性质和定理，如平面与平面的位置关系、直线与平面的位置关系等。

通过学习立体几何，我们可以更好地理解和解决与空间有关的问题。

五、数列与数学归纳法数列是数学中的一种重要概念，它是按照一定规律排列的一系列数的集合。

在高一数学中，我们将学习到数列的定义、性质和特殊数列的求和公式。

数学归纳法则是数学中证明问题的一种有效方法，通过归纳法可以证明一般性的结论。

高三数学知识点梳理第14章空间直线与平面1、内容要目：平面的概念及其表示方法，平面的基本性质，用“斜二测”方法画简单的直观图，简单几何体的截面，空间直线与直线的位置关系，平行公理，等角定理，异面直线的概念，异面直线所成的角，空间直线与平面的位置关系，空间平面与平面的位置关系。

2、基本要求：掌握画空间图形的基本技能，培养空间想象能力，理解异面直线所成角的概念，会画简单图形中的异面直线所成角的大小。

3、重难点：平面的基本性质和平行线的传递性，空间直线和直线、直线和平面、平面和平面的位置关系及其各种表示法，用反证法证明两条直线是异面直线，运用平面的基本性质进行说理证明问题。

观图中的长度分别是0.5cm、1cm、1cm.2、祖恒定理：用一组平行线去截两个空间图形，若在任意等高处的截面面积相等，则这两空间图形的体积必然相等。

3、多面体和旋转体共同性质和度量公式：4、设几何体的底面周长为c （有两个不同底面时，周长分别记为21c c ，），母线或斜高长为'h .(1) 圆柱和直棱柱的表面积分别为圆柱S ='22ch c +π，=直S 'ch +地面面积2⨯(2) 圆锥和正棱锥的表面积分别为=圆锥S 2'2ch c +π，'21ch S =正+底面面积 (3) 半径为r 的球的表面积为=球S 24r π. 5、球面距离：通过球面上两点的大圆劣弧的弧长。

第16章 排列组合和二项式定理1、乘法原理：如果完成一件事需要n 个步骤，第1步有1m 种不同的方法，第2步有2m 种不同的方法，……，第n 步有n m 种不同的方法，那么完成这件事共有n m m m N Λ21=种不同的方法。

2、加法原理：如果完成一件事有n 类办法，在第1类办法中有1m 种不同的方法，在第2类办法中有2m 种不同的方法，……，在第n 类办法中有n m 种不同的方法，那么完成这件事共有n m m m N +++=Λ21种不同的方法。

目录一、集合与常用逻辑二、不等式三、函数概念与性质四、基本初等函数五、函数图像与方程六、三角函数七、数列八、平面向量九、复数与推理证明十、直线与圆十一、曲线方程十二、矩阵、行列式、算法初步十三、立体几何十四、计数原理十五、概率与统计一、集合与常用逻辑1．集合概念元素：互异性、无序性2．集合运算全集U：如U=R交集:并集：补集:3．集合关系空集子集：任意注：数形结合———文氏图、数轴4．四种命题原命题:若p则q逆命题：若q则p 否命题：若则逆否命题：若则原命题逆否命题否命题逆命题5．充分必要条件p是q的充分条件：p是q的必要条件：p是q的充要条件:p⇔q6．复合命题的真值①q真（假）⇔“"假（真）②p、q同真⇔“p∧q”真③p、q都假⇔“p∨q"假7。

全称命题、存在性命题的否定∀∈M， p(x）否定为: ∃∈M，∃∈M， p(x）否定为: ∀∈M，二、不等式1．一元二次不等式解法若,有两实根,则解集解集注:若，转化为情况2．其它不等式解法-转化或（）(）3．基本不等式①②若，则注:用均值不等式、求最值条件是“一正二定三相等”三、函数概念与性质1．奇偶性f(x）偶函数f（x）图象关于轴对称f(x）奇函数f（x）图象关于原点对称注：①f（x)有奇偶性定义域关于原点对称②f（x）奇函数,在x=0有定义f(0）=0③“奇+奇=奇”（公共定义域内)2．单调性f（x)增函数：x1＜x2f(x1）＜f(x2）或x1＞x2f(x1）＞f（x2)或f(x）减函数：？注：①判断单调性必须考虑定义域②f(x）单调性判断定义法、图象法、性质法“增+增=增”③奇函数在对称区间上单调性相同偶函数在对称区间上单调性相反3．周期性是周期恒成立(常数)4．二次函数解析式： f（x）=ax2+bx+c，f（x）=a(x-h）2+kf（x)=a（x-x1)（x-x2）对称轴: 顶点：单调性：a〉0，递减,递增当，f(x）min奇偶性：f(x）=ax2+bx+c是偶函数b=0闭区间上最值：配方法、图象法、讨论法-——注意对称轴与区间的位置关系注：一次函数f(x）=ax+b奇函数b=0四、基本初等函数1．指数式2．对数式（a〉0，a≠1）注:性质常用对数，自然对数，3．指数与对数函数y=a x与y=log a x定义域、值域、过定点、单调性？注:y=a x与y=log a x图象关于y=x对称（互为反函数) 4．幂函数在第一象限图象如下：五、函数图像与方程1．描点法函数化简→定义域→讨论性质（奇偶、单调)取特殊点如零点、最值点等2．图象变换平移:“左加右减，上正下负”伸缩：对称：“对称谁，谁不变，对称原点都要变”注：翻折：保留轴上方部分，并将下方部分沿轴翻折到上方保留轴右边部分,并将右边部分沿轴翻折到左边3．零点定理若，则在内有零点（条件：在上图象连续不间断)注：①零点：的实根②在上连续的单调函数,则在上有且仅有一个零点③二分法判断函数零点-——?六、三角函数1．概念第二象限角（)2．弧长扇形面积3．定义其中是终边上一点，4．符号“一正全、二正弦、三正切、四余弦" 5．诱导公式：“奇变偶不变，符号看象限”如,6．特殊角的三角函数值7．基本公式同角和差倍角降幂cos2α= sin2α=叠加8．三角函数的图象性质单调性：增减增注:9．解三角形基本关系：sin（A+B）=sinC cos（A+B）=—cosCtan（A+B）=—tanC正弦定理：==余弦定理：a2=b2+c2－2bc cos A(求边）cos A=(求角）面积公式：S△＝ab sin C注：中,A+B+C=？a2＞b2+c2 ⇔∠A＞七、数列1、等差数列定义：通项:求和：中项:（成等差）性质:若，则2、等比数列定义：通项：求和：中项：(成等比)性质：若则3、数列通项与前项和的关系4、数列求和常用方法公式法、裂项法、错位相减法、倒序相加法八、平面向量1．向量加减三角形法则，平行四边形法则首尾相接，=共始点中点公式：是中点2．向量数量积 ==注：①夹角：00≤θ≤1800②同向:3．基本定理（不共线——基底）平行：（）垂直：模：＝夹角:注：①∥②（结合律)不成立③（消去律）不成立九、复数与推理证明1．复数概念复数：(a，b，实部a、虚部b分类:实数（)，虚数（），复数集C注：是纯虚数,相等：实、虚部分别相等共轭：模：复平面：复数z对应的点2．复数运算加减：（a+bi）±(c+di）=？乘法：（a+bi)（c+di）=？除法： ===…乘方：，3．合情推理类比:特殊推出特殊归纳：特殊推出一般演绎：一般导出特殊（大前题→小前题→结论）4．直接与间接证明综合法：由因导果比较法：作差-变形—判断—结论反证法：反设—推理—矛盾—结论分析法：执果索因分析法书写格式：要证A为真，只要证B为真,即证……，这只要证C为真,而已知C为真，故A必为真注:常用分析法探索证明途径，综合法写证明过程5．数学归纳法：（1)验证当n=1时命题成立,（2)假设当n=k(k∈N＊ ,k≥1)时命题成立，证明当n=k+1时命题也成立由(1）（2）知这命题对所有正整数n都成立注：用数学归纳法证题时,两步缺一不可，归纳假设必须使用十、直线与圆1、倾斜角范围斜率注：直线向上方向与轴正方向所成的最小正角倾斜角为时，斜率不存在2、直线方程点斜式，斜截式两点式, 截距式一般式注意适用范围：①不含直线②不含垂直轴的直线③不含垂直坐标轴和过原点的直线3、位置关系（注意条件）平行且垂直垂直4、距离公式两点间距离:|AB｜=点到直线距离：5、圆标准方程：圆心，半径圆一般方程：(条件是？）圆心半径6、直线与圆位置关系注：点与圆位置关系点在圆外7、直线截圆所得弦长十一、圆锥曲线一、定义椭圆： |PF1|+|PF2｜=2a（2a>|F1F2｜)双曲线：｜PF1｜—|PF2|=±2a(0〈2a〈|F1F2｜) 抛物线:与定点和定直线距离相等的点轨迹二、标准方程与几何性质(如焦点在x轴）椭圆（ a〉b>0）双曲线(a>0，b>0）中心原点对称轴？焦点F1（c,0)、F2（—c,0)顶点:椭圆（±a，0），（0，±b）,双曲线（±a，0）范围: 椭圆-a≤x≤a，-b≤y≤b双曲线｜x｜≥ a，y∈R焦距：椭圆2c（c=)双曲线2c（c=）2a、2b：椭圆长轴、短轴长，双曲线实轴、虚轴长离心率：e=c/a 椭圆0〈e<1，双曲线e〉1注:双曲线渐近线方程表示椭圆方程表示双曲线抛物线y2=2px（p〉0）顶点（原点）对称轴(x轴）开口（向右）范围x 0 离心率e=1焦点准线十二、矩阵、行列式、算法初步十、算法初步一．程序框图二．基本算法语句及格式1输入语句:INPUT “提示内容”;变量2输出语句:PRINT“提示内容”;表达式3赋值语句:变量=表达式4条件语句“IF—THEN-ELSE"语句“IF—THEN"语句IF 条件 THEN IF 条件 THEN 语句1 语句ELSE END IF语句2END IF5循环语句当型循环语句直到型循环语句WHILE 条件 DO循环体循环体WEND LOOP UNTIL 条件当型“先判断后循环”直到型“先循环后判断" 三．算法案例1、求两个数的最大公约数辗转相除法:到达余数为0更相减损术:到达减数和差相等2、多项式f（x）= a n x n+a n—1x n—1+…。

目录一、集合与常用逻辑补集：C A {x x U x A}U 且二、不等式三、函数概念与性质3．集合关系空集 A四、基本初等函数子集A B : 任意x A x B五、函数图像与方程六、三角函数A B A A B A B B A B七、数列注：数形结合--- 文氏图、数轴八、平面向量4．四种命题九、复数与推理证明原命题：若p则q逆命题：若q则p十、直线与圆否命题：若p则q逆否命题：若q则p十一、曲线方程原命题逆否命题否命题逆命题十二、矩阵、行列式、算法初步5．充分必要条件十三、立体几何p 是q 的充分条件：P q十四、计数原理p 是q 的必要条件：P q十五、概率与统计p 是q 的充要条件：p? q6．复合命题的真值①q 真（假）? “q ”假（真）一、集合与常用逻辑②p、q 同真? “p∧q”真1．集合概念元素：互异性、无序性③p、q 都假? “p∨q”假2．集合运算全集U：如U=R7. 全称命题、存在性命题的否定交集：A B { x x A且x B}M, p(x ）否定为:M, p( X )M, p(x ）否定为:M, p( X ) 并集：A B { x x A或x B}二、不等式三、函数概念与性质1．一元二次不等式解法2bx c若 a 0 ，ax 0 有两实根 , () ，则1．奇偶性2bx cax解集( , )f (x) 偶函数f ( x)f (x)f(x) 图象关于 y 轴对称2bx cax 0解集( , ) ( ,)f (x) 奇函数f ( x)f (x)f(x) 图象关于原点对称注：若 a 0，转化为 a 0 情况 注：①f(x) 有奇偶性定义域关于原点对称②f(x) 奇函数 , 在 x=0 有定义f(0)=02．其它不等式解法 —转化x a a x a2a 2x③“奇+奇=奇”（公共定义域内）2．单调性x ax a或x a2a 2xf (x) 增函数： x 1＜x 2f(x 1) ＜f(x 2) 或 x 1＞x 2f(x 1) ＞f(x 2)f (x) x)g(f (x)g (x) 0f (x ) f (x )12或xx12f ( x )a g x( )af ( x)g (x) （a 1）f(x) 减函数：？log a f ( x) log a g(x)f (x) 0f (x) g( x)（0 a 1）注：①判断单调性必须考虑定义域②f(x) 单调性判断3．基本不等式 定义法、图象法、性质法“增+增=增”① a 2b 2 2ab③奇函数在对称区间上单调性相同a b②若a,b R ，则ab2注：用均值不等式 a b 2 ab 、a bab ( )22偶函数在对称区间上单调性相反3．周期性T 是f(x)周期f(x T) f (x) 恒成立（常数T 0）求最值条件是“一正二定三相等”4．二次函数解析式：f(x)=ax 2+bx+c，f(x)=a(x-h) 2+kf(x)=a(x-x 1)(x-x 2)对称轴：xb2a2b 4 ac b顶点：( , )2 a 4 anl o g a b l o g bna1l o gba b单调性：a>0，]( ,2 ab递减，[ , )2 a递增log N注：性质log a 1 0 log a a 1 a a N常用对数lg N log10 N ，l g 2 lg 5 1当xb2a，f(x) min4 ac4 ab 2自然对数N Nln log ，ln e1e3．指数与对数函数y=ax 与y=logx 与y=loga x奇偶性：f(x)=ax 2+bx+c 是偶函数b=0闭区间上最值：配方法、图象法、讨论法---注意对称轴与区间的位置关系注：一次函数f(x)=ax+b 奇函数b=0定义域、值域、过定点、单调性？x注：y=a 与y=log a x 图象关于y=x 对称（互为反函数）1四、基本初等函数4．幂函数y x2, y x3, y x , y x2, y x3, y x , y x210 a 1．指数式 a 1 ( 0)a nn1 m m na anay x 在第一象限图象如下：b2．对数式log N b a Na（a>0,a ≠1）10 1 0 log a MN log a M log a NlogMa log M logNaaN nlog a M nlog a Mlogmm log ba log bal glgbayy五、函数图像与方程y=f(x)y=f(|x|) 1．描点法函数化简→定义域→讨论性质（奇偶、单调）a o b c a oxb c x取特殊点如零点、最值点等3．零点定理若f (a) f (b) 0，则y f (x) 在(a,b)内有零点2．图象变换平移：“左加右减，上正下负”（条件： f ( x) 在[ a,b] 上图象连续不间断）y f (x) y f ( x h)注：① f (x) 零点： f ( x) 0 的实根1每一点的横坐标变为原来的倍伸缩：) y f ( x) y f ( x ②在[ a, b] 上连续的单调函数 f (x) ，f (a) f (b) 0 则 f ( x) 在( a,b)上有且仅有一个零点③二分法判断函数零点--- f (a) f (b) 0 ？对称：“对称谁，谁不变，对称原点都要变”x轴y f (x) y f(x) 六、三角函数y轴y f (x) y f ( x)原点y f (x) y f ( x) 1．概念第二象限角,2 )(2k k ( k Z )2注：y f (x)直线x ay f (2a x)12．弧长l r 扇形面积S lr2翻折：y f ( x) y | f (x) |保留x轴上方部分，并将下方部分沿x轴翻折到上方3．定义sinyrcosxrtanyx 其中P( x, y)是终边上一点，PO ryyy=f(x)y=|f(x)|4．符号“一正全、二正弦、三正切、四余弦”5．诱导公式：“奇变偶不变，符号看象限”a o c a oxb bc x如Sin( 2) sin ，c os( / 2 ) siny f (x) y f (| x |)保留y 轴右边部分，6．特殊角的三角函数值并将右边部分沿y 轴翻折到左边36 4 3 2 2a2 b2a s inbc os a sin( ) (tan )bsin 0 12223 1 0 128．三角函数的图象性质y=sinx y=cosx y=tanxcos 13222121tg 033 1 3 / 0 / 图象7．基本公式sin2 tan2同角sin cos 1cos和差sin sin cos cos sincos cos cos sin sin 单调性：)( , 增(0, )减( , )增2 2 2 2tantan1 tant antansinx cosx tanx值域[-1 ，1] [-1 ，1] 无倍角sin 2 2 s in coscos2 2 sin2 2cos 1 1 2sin2 2cos 奇偶奇函数偶函数奇函数tan 21 2 tan2tan周期2π2ππ对称轴x k / 2 x k无降幂cos 2α=1 cos22sin 2 1α =cos22中心k ,0/ 2 k ,0k / 2,0叠加) sin cos 2 sin(4 注：k Z3 sin cos 2 s in( )62、等比数列9．解三角形基本关系：sin(A+B)=sinC cos(A+B)=-cosCa定义： 1 q( q0)nanA BCtan(A+B)=-tanCsincos22absincsin正弦定理：==sin ABCa 2R sin A a :b :c s i nA: s i n B: s i n C余弦定理：a2=b2+c2－2bccosA（求边）22c2bacosA =（求角）2bcn1通项：a a qn1na(q)1)(q1n求和：Sa(1qqn11)12 （a,b,c成等比）中项：b ac性质：若m n p q 则a aa amnpq 3、数列通项与前n项和的关系面积公式：S△＝12absinC ans1sna (n1sn1 (n1)2)注：ABC 中，A+B+C=？ A B sin A sin B4、数列求和常用方法2＞b2+c2 ? ∠A ＞a 2公式法、裂项法、错位相减法、倒序相加法七、数列八、平面向量1．向量加减三角形法则，平行四边形法则1、等差数列定义：a n 1 a n d通项：a n a1 (n 1)d AB AC 首尾相接，OB OC =CB 共始点BCn(a1 a n ) 1 求和：中项：中点公式：AB AC 2AD D 是BC 中点a b cos2．向量数量积 a b == x1x2 y1 y 2注：① a , b 夹角：00≤θ≤180S na n(n 1)dn 12 2a cb （a,b,c成等差）2性质：若m n p q ，则a m a a an p q 0≤θ≤180②a,b同向：a b a b 模：z a 2 b2z z z 23．基本定理 a 1e e （e1 ,e2 不共线-- 基底）1 2 2复平面：复数z 对应的点(a, b)平行：a // b a b x1y x y （b0）2 2 1 2．复数运算加减：（a+bi ）±(c+di)= ？垂直：a b a b 0 x1x2 y1 y2 0模：a＝22 y2x a b (a b)2乘法：（a+bi ）（c+di ）=？除法：acb idi=(a(cb i)(cci )(didi2乘方： 1i ，ni i 4kir))==,r夹角：cosa b| a ||b |3．合情推理类比：特殊推出特殊归纳：特殊推出一般注：①0 ∥a ②a b c a b c （结合律）不成立演绎：一般导出特殊（大前题→小前题→结论）4．直接与间接证明综合法：由因导果③a b a c b c （消去律）不成立比较法：作差—变形—判断—结论反证法：反设—推理—矛盾—结论分析法：执果索因九、复数与推理证明分析法书写格式：要证 A 为真，只要证 B 为真，即证,, ，这只要证C为真，而已知C为真，故 A 必为真1．复数概念注：常用分析法探索证明途径，综合法写证明过程复数：z a bi (a,b R) ，实部a、虚部 b5．数学归纳法：分类：实数（ b 0），虚数（ b 0），复数集 C(1) 验证当n=1 时命题成立,z 是纯虚数 a 0，b 0注：(2) 假设当n=k(k N* ，k 1) 时命题成立,相等：实、虚部分别相等证明当n=k+1 时命题也成立z a bi共轭：由(1)(2) 知这命题对所有正整数n 都成立注：用数学归纳法证题时，两步缺一不可，归纳假设必须使用1、倾斜角范围0, 十、直线与圆 2y Dx Ey F2圆一般方程：0x （条件是？）D E圆心,2 2半径r 2 24D E F2斜率k tan y y2 1x x2 16、直线与圆位置关系注：直线向上方向与x轴正方向所成的最小正角位置关系相切相交相离倾斜角为90 时，斜率不存在2、直线方程几何特征 d r d r d r 点斜式y y0 k( x x0) ，斜截式y kx b 代数特征△0 △0 △0两点式Ax By C 0 一般式yy2y1y1xx2x1x1x y，截距式 1a b 注：点与圆位置关系 2 2 2(x a y b r 点0 ) ( )P x0 ,y0 在圆外注意适用范围：①不含直线x x7、直线截圆所得弦长②不含垂直x 轴的直线③不含垂直坐标轴和过原点的直线2 2 AB 2 r d3、位置关系（注意条件）平行k k 且b1 b21 2垂直4、距离公式k1k2 1 垂直A1 A2 B1B2 0十一、圆锥曲线两点间距离：|AB|= 2(x1 x ) ( y y )2 1 2 2一、定义椭圆：|PF 1|+|PF 2|=2a(2a>|F 1F2|)点到直线距离：d A x By C0 02 2A B双曲线：|PF 1|-|PF 2|= ±2a(0<2a<|F 1F2|)抛物线：与定点和定直线距离相等的点轨迹5、圆标准方程： 2 ( )2 2(x a) y b r 圆心( a , b ) ，半径r二、标准方程与几何性质（如焦点在x 轴）2 2x y椭圆 1( a>b>0)2 2a b 十二、矩阵、行列式、算法初步2 2x y双曲线 1(a>0,b>0)2 2a b十、算法初步中心原点对称轴？焦点F1(c,0) 、F2(-c,0)一．程序框图顶点: 椭圆( ±a,0),(0, ±b) ，双曲线( ±a,0)程序框名称功能范围: 椭圆-a x a,-b y b起止框起始和结束双曲线|x| a ，y R输入和输出的信息焦距：椭圆2c（c= 2 b2a ）输入、输出框赋值、计算双曲线2c（c= 2 b2a ）处理框判断某一条件是否成立2a、2b: 椭圆长轴、短轴长，判断框双曲线实轴、虚轴长离心率：e=c/a 椭圆0<e<1, 双曲线e>1循环框重复操作以及运算2 2x y b注：双曲线1渐近线xy2 2a b a2 ny2方程m x 1表示椭圆m 0,n 0.m n2 ny2方程m x 1表示双曲线mn 0二．基本算法语句及格式抛物线y2=2px(p>0)2=2px(p>0)1输入语句：INPUT “提示内容”；变量2 输出语句：PRINT“提示内容”；表达式顶点（原点）对称轴（x 轴）3 赋值语句：变量=表达式开口（向右）范围x 0 离心率e=1p焦点,0)F ( 准线2 xp24 条件语句“IF —THEN—ELSE”语句“IF —THEN”语句例 1 辗转相除法求得123 和 48 最大公约数为 3 IF 条件 THEN IF 条件 THEN语句1 语句例 2 已知 f(x)=2x5－5x 4－ 4x 3+3x 2－6x+7，秦九韶算法求 f(5) 123＝2×48＋ 27 v 0=2 ELSE END IF48＝1×27＋ 21 v 1=2× 5－5=5语句227 ＝1×21＋ 6v 2=5×5－4=21END IF21＝3× 6＋3 v 3=21×5+3=108 5 循环语句6＝2×3 +0v4=108×5－6=534当型循环语句直到型循环语句 WHILE 条件 DOv 5=534×5+7=2677循环体 循环体 WENDLOOP UNTIL条件当型“先判断后循环”直到型“先循环后判断”十三、立体几何三．算法案例1、求两个数的最大公约数 1． 三视图 正视图、侧视图、俯视图辗转相除法：到达余数为2．直观图 ：斜二测画法' ' ' 0X OY =45更相减损术：到达减数和差相等 平行 X 轴的线段，保平行和长度2、多项式f (x)= a n x n+a n-1x n-1+⋯ .+a 1x+a 0 的求值n +a n-1x n-1+⋯ .+a 1x+a 0 的求值平行 Y 轴的线段，保平行， 长度变原来一半秦九韶算法 ： v 1=a n x+a n－1 v 2=v 1x+a n－23． 体积与侧面积v 3=v 2x+a n－3v n =v n －1x+a 0注：递推公式v 0=a n v k =v k－1X +a n －k (k=1,2, ⋯n)求 f(x)n值，乘法、加法均最多次V 柱=S 底 h V锥=1 3S 底 h V球=4 33πR3、进位制间的转换S 圆锥侧=rl S 圆台侧=(R r)l S24 R 球表=k 进制数转换为十进制数：4．公理与推论确定一个平面的条件：n n 1a a 1.....a a (k) a k a k ......... a k an n 1 0 n n 1 1 0①不共线的三点②一条直线和这直线外一点十进制数转换成k进制数：“除k 取余法”③两相交直线④两平行直线若两个平面垂直，则一个平面内垂直于交公理：平行于同一条直线的两条直线平行P 定理：如果两个角的两条边分别对应平行，那么这两个角相等或互补。

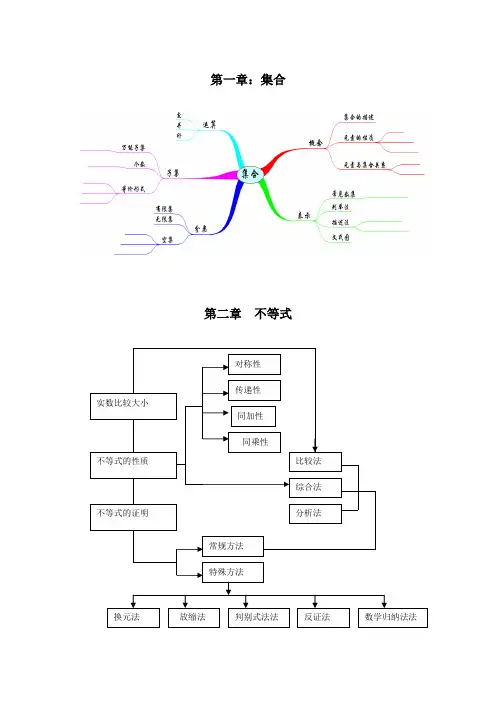
第一章：集合第二章不等式同加性传递性同乘性对称性不等式的性质实数比较大小不等式的证明综合法分析法比较法常规方法特殊方法换元法放缩法判别式法法反证法数学归纳法法第3-5章函数定义定义域区间对应法则值域一元二次函数一元二次不等式映射函数性质奇偶性单调性周期性指数函数根式分数指数指数函数的图像和性质指数方程对数方程反函数互为反函数的函数图像关系对数函数对数对数的性质积、商、幂与根的对数对数恒等式和不等式常用对数自然对数对数函数的图像和性质解不等式一元二次不等式绝对值不等式分式不等式第六章 三角比知识梳理A ． 三角比1. 在弧度制下，扇形弧长公式||l R α=，扇形面积公式211||22S lR R α==，其中α为弧所对圆心角的弧度数；2. 三角比的定义(注意定义域）:sin α=r y ，cos α=r x ，tg α=x y ，ctg α=yx，sec α=x r ，csc α=yr； 各象限角的三角比符号: 记忆法则：第一象限全为正,二正三切四余弦. 3.三角函数线:若02πα<<，则sin tan ααα<<正弦线：MP; 余弦线：OM; 正切线： AT.4. 诱导公式，奇变偶不变，符号看象限；5. 同角关系:任意角 的概念角度制与 弧度制任意角的 三角比弧长与扇形 面积公式三角函数的 图象和性质和 角 公 式 差 角 公 式几个三角 恒等式倍 角 公 式 同角三角比的关系 诱 导公 式正弦定理与余弦定理解斜三角形及其应用化简、计算、求值 与证明TMA OPxy（1）平方关系(3个): 222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= （2）倒数关系（3个）: tan cot 1,sin csc 1,cos sec 1αααααα===（3）商数关系（2个）: sin cos tan (cos 0),cot (sin 0)cos sin αααααααα=≠=≠6. 两角和与差的公式，βαβαβαsin sin cos cos )cos(-=+βαβαβαsin sin cos cos )cos(+=-βαβαβαcos sin cos sin )sin(+=+βαβαβαcos sin cos sin )sin(-=-βαβαβαtan tan 1tan tan )tan(-+=+βαβαβαtan tan 1tan tan )tan(+-=-7. 二倍角公式，θθθcos sin 22sin =ααα22sin cos 2cos -=1cos 22-=αα2sin 21-=θθθ2tan 1tan 22tan -=8.半角公式是：2cos 12cosθθ+±= 2cos 12sin θθ-±= θθθcos 1cos 12tan+-±= θθθθsin cos 1cos 1sin -=+=9. 升幂公式是：2cos2cos 12αα=+； 2sin2cos 12αα=-；110. 降幂公式是：22cos 1sin 2αα-=； 22cos 1cos 2αα+=； 11. 万能公式：sin α=22tan21tan 2αα+ cos α=221tan 21tan 2αα-+ tan α=22tan21tan 2αα-；12. 辅助角公式：sin cos )),tan ;a b b aαααααφφ+=+=+=其中13、解三角形 （1）正弦定理：R CcB b A a 2sin sin sin ===，其中R 是三角形外接圆半径. （2）余弦定理：A bc c b a cos 2222-+=,bca cb A 2cos 222-+=.（3）B ac A bc C ab S ABC sin 21sin 21sin 21===∆, Sr c S b S a S S S =---=∆))()(((2cb a S ++=,r 为内切圆半径） =Rabc4 （R 为外接圆半径）。

高一(上)数学知识点归纳第一章集合与命题5.集合的运算：(1)交集：A B{x x A且x B}.(2)并集:A B{x x A或x B}.（3）补集：C A{x x U且x A}.UPP5.真子集，交集，并集，全集，补集。

6.命题，逆命题，否命题，逆否命题，等价命题。

7充分条件与必要条件。

2. 如果a b,那么a c b c.116.如果a b0，那么0.a b7.如果a b0，那么a b(n N).n n8.如果a b0,那么a b(n N,n1).n n一元二次不等式的解法：这个知识点很重要，可根据与0的关系来求解，注意两个基本不等式：1.对于任意实数a和b,有a b2ab,当且仅当时等号a b22a b222.对任意正数a和b,有ab，当且仅当时等号2a ba b22成立。

我们把2求函数值f(a)，会求简单函数的定义域和值域。

理解函数运算意义，会求两个函数的和与积。

掌握函数奇偶性、单调性、周期性概念，会求一些简单函数的最大值和最小值。

⑵函数讲到奇偶性时其定义域一定要关于原点对称。

⑶偶函数的性质：f(x)= f(x).就是函数y f(x)的图像与轴的交点的横坐标.x注意：1.幂函数的定义：一般地，函数 y x (k 为常数，k Q ) 叫做幂函数。

k x指数函数的性质：1.指数函数 y a 的函数值恒大于零.性质x 2.指数函数 y a 的图像经过点（0，1）. x 3.函数 y a （ >1）在内是增函数； ( , )a x 函数 y a (0< <1)在内是减函数. ( , )a x 高一(下)数学知识点归纳说明：①幂函 数 y x ( Q,是常数 )的定义域 D 由常 数 确定，但 总有在（0， ）是增函数；当 时， 在（0，+）上是减函数， + y xy x 0 ②指数函数 y a (a 0,且a 1)有些同学常会与幂函数 y x ( Q,是常数)xba④函数y f(x)的定义域是它的反函数y f(x)的值域；函数的值域y f(x)1⑤对数函数y log x(a0,且a1)与指数函数y a(a0,且a1)互为反函数。

目录一、集合与常用逻辑 二、不等式 三、函数概念与性质 四、基本初等函数 五、函数图像与方程 六、三角函数 七、数 列 八、平面向量 九、复数与推理证明 十、直线与圆 十一、曲线方程十二、矩阵、行列式、算法初步 十三、立体几何 十四、计数原理 十五、概率与统计一、集合与常用逻辑1．集合概念 元素：互异性、无序性 2．集合运算 全集U ：如U=R 交集：}{B x A x x B A ∈∈=且I 并集：}{B x A x x B A ∈∈=⋃或 补集：}{A x U x x A C U ∉∈=且3．集合关系 空集A ⊆φ子集B A ⊆:任意B x A x ∈⇒∈B A B B A BA AB A ⊆⇔=⊆⇔=Y I注：数形结合---文氏图、数轴 4．四种命题原命题：若p 则q 逆命题：若q 则p 否命题：若p ⌝则q ⌝ 逆否命题：若q ⌝则p ⌝原命题⇔逆否命题 否命题⇔逆命题5．充分必要条件p 是q 的充分条件：q P ⇒ p 是q 的必要条件：q P ⇐ p 是q 的充要条件：p ⇔q 6．复合命题的真值①q 真（假）⇔“q ⌝”假（真） ②p 、q 同真⇔“p ∧q ”真 ③p 、q 都假⇔“p ∨q ”假 7.全称命题、存在性命题的否定M, p(x ）否定为: M, )(X p ⌝ M, p(x ）否定为: M, )(X p ⌝二、不等式1．一元二次不等式解法若0>a ，02=++c bx ax 有两实根βα,)(βα<，则02<++c bx ax 解集),(βα02>++c bx ax 解集),(),(+∞-∞βαY注：若0<a ，转化为0>a 情况 2．其它不等式解法—转化a x a a x <<-⇔<⇔22a x <⇔>a x a x >或a x -<⇔22a x >0)()(>x g x f ⇔0)()(>x g x f ⇔>)()(x g x f a a )()(x g x f >（a >1）⇔>)(log )(log x g x f a a f x f x g x ()()()><⎧⎨⎪⎩⎪0（01<<a ）3．基本不等式 ①ab b a 222≥+②若+∈R b a ,，则ab ba ≥+2注：用均值不等式ab b a 2≥+、2)2(b a ab +≤ 求最值条件是“一正二定三相等”三、函数概念与性质1．奇偶性f(x)偶函数⇔()()f x f x -=⇔f(x)图象关于y 轴对称 f(x)奇函数⇔()()f x f x -=-⇔f(x)图象关于原点对称 注：①f(x)有奇偶性⇒定义域关于原点对称②f(x)奇函数,在x=0有定义⇒f(0)=0 ③“奇+奇=奇”（公共定义域内）2．单调性f(x)增函数：x 1＜x 2⇒f(x 1)＜f(x 2)或x 1＞x 2⇒f(x 1) ＞f(x 2) 或0)()(2121>--x x x f x ff(x)减函数：？注：①判断单调性必须考虑定义域②f(x)单调性判断定义法、图象法、性质法“增+增=增” ③奇函数在对称区间上单调性相同 偶函数在对称区间上单调性相反 3．周期性T 是()f x 周期⇔()()f x T f x +=恒成立（常数0≠T）4．二次函数解析式： f(x)=ax 2+bx+c ，f(x)=a(x-h)2+k f(x)=a(x-x 1)(x-x 2)对称轴：abx 2-= 顶点：)44,2(2a b ac a b -- 单调性：a>0，]2,(ab--∞递减，),2[+∞-a b 递增 当ab x 2-=，f(x)min a b ac 442-=奇偶性：f(x)=ax 2+bx+c 是偶函数⇔b=0 闭区间上最值：配方法、图象法、讨论法--- 注意对称轴与区间的位置关系注：一次函数f(x)=ax+b 奇函数⇔b=0四、基本初等函数1．指数式 )0(10≠=a a n n a a 1=- m n m na a =2．对数式 b N a =log N a b=⇔（a>0,a ≠1）N M MN a a a log log log +=N M NM a a a log log log -=M n M a n a log log =a b b m m a log log log =ablg lg =na ab b n log log =ab log 1=注：性质01log =a 1log =a a N aNa =log常用对数N N 10log lg =，15lg 2lg =+ 自然对数N N e log ln =，1ln =e 3．指数与对数函数 y=a x 与y=log a x定义域、值域、过定点、单调性？注：y=a x 与y=log a x 图象关于y=x 对称（互为反函数） 4．幂函数 12132,,,-====x y x y x y x yαx y =在第一象限图象如下：、函数图像与方程1．描点法α>101<<αα<0函数化简→定义域→讨论性质（奇偶、单调） 取特殊点如零点、最值点等 2．图象变换平移：“左加右减，上正下负”)()(h x f y x f y +=→=伸缩：)1()(x f y x f y ϖϖ=−−−−−−−−→−=倍来的每一点的横坐标变为原对称：“对称谁，谁不变，对称原点都要变”)()()()()()(x f y x f y x f y x f y x f y x f y y x --=−−→−=-=−→−=-=−→−=原点轴轴注：)(x f y =ax =→直线)2(x a f y -=翻折：→=)(x f y |()|y f x =保留x 轴上方部分，并将下方部分沿x 轴翻折到上方→=)(x f y (||)y f x =保留y 轴右边部分， 并将右边部分沿y 轴翻折到左边3．零点定理若0)()(<b f a f ，则)(x f y =在),(b a 内有零点 （条件：)(x f 在],[b a 上图象连续不间断）注：①)(x f 零点：0)(=x f 的实根②在],[b a 上连续的单调函数)(x f ，0)()(<b f a f则)(x f 在),(b a 上有且仅有一个零点③二分法判断函数零点---0)()(<b f a f ？六、三角函数1．概念 第二象限角)2,22(ππππ++k k (Z k ∈)2．弧长 r l ⋅=α 扇形面积lr S 21=3．定义 r y =αsin r x =αcos xy=αtan 其中),(y x P 是α终边上一点，r PO =4．符号 “一正全、二正弦、三正切、四余弦” 5．诱导公式：“奇变偶不变，符号看象限”如ααπsin )2(-=-Sin ，ααπsin )2/cos(-=+ 6．特殊角的三角函数值7．基本公式 同角1cos sin22=+αααααtan cos sin = 和差()βαβαβαsin cos cos sin sin ±=±()βαβαβαsin sin cos cos cos μ=± ()βαβαβαtan tan 1tan tan tan μ±=±倍角 αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα2tan 1tan 22tan -=降幂cos 2α=22cos 1α+ sin 2α=22cos 1α- 叠加 )4sin(2cos sin πααα+=+)6sin(2cos sin 3πααα-=-)sin(cos sin 22ϕααα++=+b a b a )(tan ba=ϕ8．三角函数的图象性质单调性： )2,2(ππ-增 ),0(π减 )2,2(ππ-增 注：Z k ∈9．解三角形tan(A+B)=-tanC 2cos 2sinCB A =+ 正弦定理：A a sin =B b sin =Ccsin A R a sin 2= C B A c b a sin :sin :sin ::=余弦定理：a 2=b 2+c 2－2bc cos A （求边）cos A =bca cb 2222-+（求角）面积公式：S △＝21ab sin C 注：ABC ∆中，A+B+C=？ B A B A sin sin <⇔<a 2＞b 2+c 2 ⇔ ∠A ＞2π七、数 列1、等差数列定义：d a a n n =-+1 通项：d n a a n )1(1-+= 求和：2)(1n n a a n S += d n n na )1(211-+= 中项：2ca b +=（c b a ,,成等差） 性质：若q p n m +=+，则q p n m a a a a +=+2、等比数列 定义：)0(1≠=+q q a a nn通项：11-=n n q a a求和：⎪⎩⎪⎨⎧≠--==)1(1)1()1(11q qq a q na S nn中项：ac b =2（c b a ,,成等比）性质：若q p n m +=+ 则q p n m a a a a ⋅=⋅ 3、数列通项与前n 项和的关系⎩⎨⎧≥-===-)2()1(111n s s n a s a n nn4、数列求和常用方法公式法、裂项法、 错位相减法、倒序相加法八、平面向量1．向量加减 三角形法则，平行四边形法则=+BC AB AC 首尾相接，OC OB -=CB 共始点中点公式：⇔=+AD AC AB 2D 是BC 中点2． 向量数量积 ⋅=θcos ⋅⋅=2121y y x x +注：①b a ,夹角：00≤θ≤1800②b a ,同向：b a =⋅ 3．基本定理 2211e e a ρρρλλ+=（21,e e ρρ不共线--基底） 平行：⇔b a //b a λ=⇔1221y x y x =（≠） 垂直：0=⋅⇔⊥b a b a 02121=+⇔y y x x模：a ρ＝22y x +Λ=+=+2)(夹角：=θcos ||||b a注：①0ρ∥a ②()()c b a c b a ⋅⋅≠⋅⋅（结合律）不成立③c a b a ⋅=⋅c b =⇒（消去律）不成立九、复数与推理证明1．复数概念复数：bi a z +=(a,b )R ∈，实部a 、虚部b 分类：实数（0=b ），虚数（0≠b ），复数集C注：z 是纯虚数0=⇔a ，0≠b相等：实、虚部分别相等 共轭：bi a z -= 模：22b a z +=2z z z =⋅复平面：复数z 对应的点),(b a 2．复数运算加减：（a+bi ）±(c+di)=？ 乘法：（a+bi ）（c+di ）=？除法： di c bi a ++=))(())((di c di c di c bi a -+-+==…乘方：12-=i ，=n i rrk i i=+43．合情推理类比：特殊推出特殊归纳：特殊推出一般演绎：一般导出特殊（大前题→小前题→结论） 4．直接与间接证明综合法：由因导果比较法：作差—变形—判断—结论 反证法：反设—推理—矛盾—结论 分析法：执果索因分析法书写格式：要证A 为真，只要证B 为真，即证……，这只要证C 为真，而已知C 为真，故A 必为真注：常用分析法探索证明途径，综合法写证明过程 5．数学归纳法：(1)验证当n=1时命题成立,(2)假设当n=k(k ÎN* ，k ³1)时命题成立, 证明当n=k+1时命题也成立由(1)(2)知这命题对所有正整数n 都成立注：用数学归纳法证题时，两步缺一不可，归纳假设必须使用十、直线与圆1、倾斜角 范围[)0,π 斜率 2121tan y y k x x α-==-注：直线向上方向与轴正方向所成的最小正角倾斜角为90︒时，斜率不存在 2、直线方程点斜式)(00x x k y y -=-，斜截式b kx y += 两点式121121x x x x y y y y --=--， 截距式1=+bya x一般式0=++C By Ax注意适用范围：①不含直线0x x =②不含垂直x 轴的直线③不含垂直坐标轴和过原点的直线 3、位置关系（注意条件） 平行⇔12k k = 且21b b ≠垂直⇔121k k =- 垂直⇔12120A A B B += 4、距离公式两点间距离：|AB|=221221)()(y y x x -+- 点到直线距离：0022Ax By Cd A B++=+5、圆标准方程：222)()(r b y a x =-+- 圆心),(b a ，半径r圆一般方程：022=++++F Ey Dx y x （条件是？）圆心,22D E ⎛⎫-- ⎪⎝⎭ 半径2242D E Fr +-=6、直线与圆位置关系注：点与圆位置关系 ⇔>-+-22020)()(r b y a x 点()00,P x y 在圆外7、直线截圆所得弦长222AB r d =-十一、圆锥曲线一、定义椭圆： |PF 1|+|PF 2|=2a(2a>|F 1F 2|) 双曲线：|PF 1|-|PF 2|=±2a(0<2a<|F 1F 2|) 抛物线：与定点和定直线距离相等的点轨迹 二、标准方程与几何性质（如焦点在x 轴）椭圆12222=+b y a x ( a>b>0)双曲线12222=-by a x (a>0,b>0)中心原点 对称轴？ 焦点F 1(c,0)、F 2(-c,0) 顶点: 椭圆(±a,0),(0, ±b)，双曲线(±a,0) 范围: 椭圆-a x a,-b y b双曲线|x| a ，y R 焦距：椭圆2c （c=22b a -）双曲线2c （c=22b a +） 2a 、2b :椭圆长轴、短轴长，双曲线实轴、虚轴长离心率：e=c/a 椭圆0<e<1,双曲线e>1注：双曲线12222=-by a x 渐近线x a by ±=方程122=+ny mx 表示椭圆n m n m ≠>>⇔.0,0方程122=+ny mx 表示双曲线0<⇔mn抛物线y 2=2px(p>0)顶点（原点） 对称轴（x 轴）开口（向右） 范围x 0 离心率e=1焦点)0,2(p F准线2px -= 十二、矩阵、行列式、算法初步1. 矩阵是记录和管理批量数据的一种方法从具体问题人手，通过构造矩阵，利用矩阵的运算解决问题．由n m ⨯个数排成的m 行n 列的矩形表⎪⎪⎪⎪⎪⎭⎫ ⎝⎛mn m m n n a a a a a a a a a .....................212222111211称为一个m 行n 列的矩阵，简称n m ⨯矩阵，用n m A ⨯表示，简记为n m ij a A ⨯=)(或),...2,1;,...2,1)((n j m i a A ij ===，数ij a 称为矩阵A 的元素。

文案大全目录一、集合与常用逻辑 二、不等式 三、函数概念与性质 四、基本初等函数 五、函数图像与方程 六、三角函数 七、数 列 八、平面向量九、复数与推理证明 十、直线与圆 十一、曲线方程十二、矩阵、行列式、算法初步 十三、立体几何 十四、计数原理 十五、概率与统计一、集合与常用逻辑1．集合概念 元素：互异性、无序性 2．集合运算 全集U ：如U=R 交集：}{B x A x x B A ∈∈=且 并集：}{B x A x x B A ∈∈=⋃或补集：}{A x U x x A C U ∉∈=且 3．集合关系 空集A ⊆φ子集B A ⊆:任意B x A x ∈⇒∈B A B B A BA AB A ⊆⇔=⊆⇔=注：数形结合---文氏图、数轴 4．四种命题原命题：若p 则q 逆命题：若q 则p 否命题：若p ⌝则q ⌝ 逆否命题：若q ⌝则p ⌝原命题⇔逆否命题 否命题⇔逆命题5．充分必要条件p 是q 的充分条件：q P ⇒ p 是q 的必要条件：q P ⇐ p 是q 的充要条件：p ⇔q 6．复合命题的真值①q 真（假）⇔“q ⌝”假（真） ②p 、q 同真⇔“p ∧q ”真 ③p 、q 都假⇔“p ∨q ”假7.全称命题、存在性命题的否定 ∀∈M, p(x ）否定为: ∃∈M, )(X p ⌝ ∃∈M, p(x ）否定为: ∀∈M, )(X p ⌝文案大全二、不等式1．一元二次不等式解法若0>a ，02=++c bx ax 有两实根βα,)(βα<，则02<++c bx ax 解集),(βα02>++c bx ax 解集),(),(+∞-∞βα注：若0<a ，转化为0>a 情况 2．其它不等式解法—转化a x a a x <<-⇔<⇔22a x <⇔>a x a x >或a x -<⇔22a x >0)()(>x g x f ⇔0)()(>x g x f ⇔>)()(x g x f a a )()(x g x f >（a >1）⇔>)(log )(log x g x f a a f x f x g x ()()()><⎧⎨⎪⎩⎪0（01<<a ）3．基本不等式 ①ab b a 222≥+②若+∈R b a ,，则ab b a ≥+2注：用均值不等式ab b a 2≥+、2)2(b a ab +≤ 求最值条件是“一正二定三相等”三、函数概念与性质1．奇偶性f(x)偶函数⇔()()f x f x -=⇔f(x)图象关于y 轴对称 f(x)奇函数⇔()()f x f x -=-⇔f(x)图象关于原点对称注：①f(x)有奇偶性⇒定义域关于原点对称②f(x)奇函数,在x=0有定义⇒f(0)=0 ③“奇+奇=奇”（公共定义域内） 2．单调性f(x)增函数：x 1＜x 2⇒f(x 1)＜f(x 2)或x 1＞x 2⇒f(x 1) ＞f(x 2) 或0)()(2121>--x x x f x ff(x)减函数：？注：①判断单调性必须考虑定义域②f(x)单调性判断定义法、图象法、性质法“增+增=增” ③奇函数在对称区间上单调性相同文案大全偶函数在对称区间上单调性相反 3．周期性T 是()f x 周期⇔()()f x T f x +=恒成立（常数0≠T）4．二次函数解析式： f(x)=ax 2+bx+c ，f(x)=a(x-h)2+k f(x)=a(x-x 1)(x-x 2)对称轴：abx 2-= 顶点：)44,2(2a b ac a b -- 单调性：a>0，]2,(ab--∞递减，),2[+∞-a b 递增 当ab x 2-=，f(x)min a b ac 442-=奇偶性：f(x)=ax 2+bx+c 是偶函数⇔b=0闭区间上最值：配方法、图象法、讨论法--- 注意对称轴与区间的位置关系注：一次函数f(x)=ax+b 奇函数⇔b=0四、基本初等函数1．指数式 )0(10≠=a a n n a a 1=- m nm na a =2．对数式 b N a =log N a b=⇔（a>0,a ≠1）N M MN a a a log log log +=N M NM a a a log log log -=M n M a n a log log =a b b m m a log log log =ablg lg =na ab b n log log =ab log 1=注：性质01log =a 1log =a a N aNa =log常用对数N N 10log lg =，15lg 2lg =+ 自然对数N N e log ln =，1ln =e 3．指数与对数函数 y=a x与y=log a x定义域、值域、过定点、单调性？注：y=a x与y=log a x 图象关于y=x 对称（互为反函数）4．幂函数 12132,,,-====x y x y x y x yαx y =在第一象限图象如下：文案大全五、函数图像与方程1．描点法函数化简→定义域→讨论性质（奇偶、单调） 取特殊点如零点、最值点等 2．图象变换平移：“左加右减，上正下负”)()(h x f y x f y +=→=伸缩：)1()(x f y x f y ϖϖ=−−−−−−−−→−=倍来的每一点的横坐标变为原对称：“对称谁，谁不变，对称原点都要变”)()()()()()(x f y x f y x f y x f y x f y x f y y x --=−−→−=-=−→−=-=−→−=原点轴轴注：)(x f y =ax =→直线)2(x a f y -=翻折：→=)(x f y |()|y f x =保留x 轴上方部分，并将下方部分沿x 轴翻折到上方→=)(x f y (||)y f x =保留y 轴右边部分， 并将右边部分沿y 轴翻折到左边3．零点定理若0)()(<b f a f ，则)(x f y =在),(b a 内有零点 （条件：)(x f 在],[b a 上图象连续不间断）注：①)(x f 零点：0)(=x f 的实根②在],[b a 上连续的单调函数)(x f ，0)()(<b f a f 则)(x f 在),(b a 上有且仅有一个零点③二分法判断函数零点---0)()(<b f a f ？六、三角函实用标准文档文案大全2．弧长 r l ⋅=α 扇形面积lr S 21=3．定义 r y =αsin r x =αcos xy=αtan其中),(y x P 是α终边上一点，r PO =4．符号 “一正全、二正弦、三正切、四余弦” 5．诱导公式：“奇变偶不变，符号看象限”如ααπsin )2(-=-Sin ，ααπsin )2/cos(-=+ 6．特殊角的三角函数值7．基本公式 同角1cos sin22=+αααααtan cos sin = 和差sin cos cos sin sin ±=± sin sin cos cos cos =± ()βαβαβαtan tan 1tan tan tan ±=±倍角 αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα2tan 1tan 22tan -=降幂cos 2α=22cos 1α+ sin 2α=22cos 1α- 叠加 )4sin(2cos sin πααα+=+文案大全)6sin(2cos sin 3πααα-=-)sin(cos sin 22ϕααα++=+b a b a )(tan ba=ϕ8．三角函数的图象性质单调性： )2,2(ππ-增 ),0(π减 )2,2(ππ-增 注：Z k ∈9．解三角形基本关系：sin(A+B)=sinC cos(A+B)=-cosCtan(A+B)=-tanC 2cos 2sin CB A =+正弦定理：A a sin =B b sin =Ccsin A R a sin 2= C B A c b a sin :sin :sin ::=余弦定理：a 2=b 2+c 2－2bc cos A （求边） cos A =bcac b 2222-+（求角）面积公式：S △＝21ab sin C注：ABC ∆中，A+B+C=？ B A B A sin sin <⇔<a 2＞b 2+c 2 ⇔ ∠A ＞2π七、数 列1、等差数列定义：d a a n n =-+1 通项：d n a a n )1(1-+= 求和：2)(1n n a a n S += d n n na )1(211-+= 中项：2ca b +=（c b a ,,成等差） 性质：若q p n m +=+，则q p n m a a a a +=+2、等比数列 定义：)0(1≠=+q q a a nn通项：11-=n n q a a求和：⎪⎩⎪⎨⎧≠--==)1(1)1()1(11q qq a q na S nn中项：ac b =2（c b a ,,成等比）性质：若q p n m +=+ 则q p n m a a a a ⋅=⋅ 3、数列通项与前n 项和的关系⎩⎨⎧≥-===-)2()1(111n s s n a s a n n n4、数列求和常用方法文案大全公式法、裂项法、 错位相减法、倒序相加法八、平面向量1．向量加减 三角形法则，平行四边形法则=+BC AB AC 首尾相接，-=CB 共始点中点公式：⇔=+AD AC AB 2D 是BC 中点 2． 向量数量积 ⋅θcos ⋅=2121y y x x +注：①b a ,夹角：00≤θ≤1800②,同向：=⋅ 3．基本定理 2211e e a λλ+=（21,e e不共线--基底） 平行：⇔//λ=⇔1221y x y x =（≠） 垂直：0=⋅⇔⊥b a b a 02121=+⇔y y x x模：a ＝22y x +=+=+2)(b a夹角：=θcos ||||b a ba 注：①0∥a ②()()⋅⋅≠⋅⋅（结合律）不成立③c a b a ⋅=⋅c b =⇒（消去律）不成立九、复数与推理证明1．复数概念复数：bi a z +=(a,b )R ∈，实部a 、虚部b 分类：实数（0=b ），虚数（0≠b ），复数集C注：z 是纯虚数0=⇔a ，0≠b相等：实、虚部分别相等 共轭：bi a z -= 模：22b a z +=2z z z =⋅复平面：复数z 对应的点),(b a 2．复数运算加减：（a+bi ）±(c+di)=？ 乘法：（a+bi ）（c+di ）=？ 除法：di c bi a ++=))(())((di c di c di c bi a -+-+==… 乘方：12-=i ，=n i rr k i i=+4 3．合情推理类比：特殊推出特殊归纳：特殊推出一般演绎：一般导出特殊（大前题→小前题→结论） 4．直接与间接证明综合法：由因导果比较法：作差—变形—判断—结论 反证法：反设—推理—矛盾—结论 分析法：执果索因分析法书写格式：文案大全要证A 为真，只要证B 为真，即证……， 这只要证C 为真，而已知C 为真，故A 必为真 注：常用分析法探索证明途径，综合法写证明过程 5．数学归纳法：(1)验证当n=1时命题成立,(2)假设当n=k(k ∈N* ，k ≥1)时命题成立, 证明当n=k+1时命题也成立由(1)(2)知这命题对所有正整数n 都成立注：用数学归纳法证题时，两步缺一不可，归纳假设必须使用十、直线与圆1、倾斜角 范围[)0,π斜率 2121tan y y k x x α-==-注：直线向上方向与x 轴正方向所成的最小正角倾斜角为90︒时，斜率不存在 2、直线方程点斜式)(00x x k y y -=-，斜截式b kx y +=两点式121121x x x x y y y y --=--， 截距式1=+bya x一般式0=++C By Ax注意适用范围：①不含直线0x x = ②不含垂直x 轴的直线③不含垂直坐标轴和过原点的直线 3、位置关系（注意条件）平行⇔12k k = 且21b b ≠垂直⇔121k k =- 垂直⇔12120A A B B += 4、距离公式两点间距离：|AB|=221221)()(y y x x -+- 点到直线距离：d =5、圆标准方程：222)()(r b y a x =-+- 圆心),(b a ，半径r圆一般方程：022=++++F Ey Dx y x （条件是？）圆心,22D E ⎛⎫-- ⎪⎝⎭半径2r =6、直线与圆位置关系 注：点与圆位置关系 ⇔>-+-22020)()(r b y a x 点()00,P x y 在圆外7、直线截圆所得弦长AB =文案大全十一、圆锥曲线一、定义椭圆： |PF 1|+|PF 2|=2a(2a>|F 1F 2|) 双曲线：|PF 1|-|PF 2|=±2a(0<2a<|F 1F 2|) 抛物线：与定点和定直线距离相等的点轨迹 二、标准方程与几何性质（如焦点在x 轴）椭圆12222=+by a x ( a>b>0)双曲线12222=-by a x (a>0,b>0)中心原点 对称轴？ 焦点F 1(c,0)、F 2(-c,0) 顶点: 椭圆(±a,0),(0, ±b)，双曲线(±a,0) 范围: 椭圆-a ≤x ≤a,-b ≤y ≤b双曲线|x| ≥ a ，y ∈R 焦距：椭圆2c （c=22b a -）双曲线2c （c=22b a +） 2a 、2b :椭圆长轴、短轴长，双曲线实轴、虚轴长离心率：e=c/a 椭圆0<e<1,双曲线e>1注：双曲线12222=-by a x 渐近线x a by ±=方程122=+ny mx 表示椭圆n m n m ≠>>⇔.0,0 方程122=+ny mx 表示双曲线0<⇔mn 抛物线y 2=2px(p>0)顶点（原点） 对称轴（x 轴） 开口（向右） 范围x ≥0 离心率e=1 焦点)0,2(p F准线2px -= 十二、矩阵、行列式、算法初步1. 矩阵是记录和管理批量数据的一种方法从具体问题人手，通过构造矩阵，利用矩阵的运算解决问题．由n m ⨯个数排成的m 行n 列的矩形表⎪⎪⎪⎪⎪⎭⎫⎝⎛mn m m n n a a a a a a a a a .....................212222111211称为一个m 行n 列的矩阵，简称n m ⨯矩阵，用n m A ⨯表示，简记为n m ij a A ⨯=)(或),...2,1;,...2,1)((n j m i a A ij ===，数ij a 称为矩阵A 的元素。

目录一、集合与常用逻辑补集：CA{x xUxA}U且二、不等式三、函数概念与性质3．集合关系空集A四、基本初等函数子集AB:任意xAxB五、函数图像与方程六、三角函数ABAABABBAB七、数列注：数形结合---文氏图、数轴八、平面向量4．四种命题九、复数与推理证明原命题：若p则q逆命题：若q则p十、直线与圆否命题：若p则q逆否命题：若q则p十一、曲线方程原命题逆否命题否命题逆命题十二、矩阵、行列式、算法初步5．充分必要条件十三、立体几何p是q的充分条件：Pq十四、计数原理p是q的必要条件：Pq十五、概率与统计p是q的充要条件：p?q6．复合命题的真值①q真（假）?“q”假（真）一、集合与常用逻辑②p、q同真?“p∧q”真1．集合概念元素：互异性、无序性③p、q都假?“p∨q”假2．集合运算全集U：如U=R7.全称命题、存在性命题的否定交集：AB{xxA且xB}M,p(x）否定为:M,p(X)M,p(x）否定为:M,p(X)并集：AB{xxA 或xB}二、不等式三、函数概念与性质1．一元二次不等式解法2bxc若a0，ax0有两实根,()，则1．奇偶性2bxcax解集(,)f(x)偶函数f(x)f(x)f(x)图象关于y轴对称2bxcax0解集(,)(,)f(x)奇函数f(x)f(x)f(x)图象关于原点对称注：若a0，转化为a0情况注：①f(x)有奇偶性定义域关于原点对称②f(x)奇函数,在x=0有定义f(0)=02．其它不等式解法—转化xaaxa 2a2x③“奇+奇=奇”（公共定义域内）2．单调性xaxa或xa 2a2x f(x)增函数：x1＜x2f(x1)＜f(x2)或x1＞x2f(x1)＞f(x2)f (x) x)g( 0 f(x)g(x)0f(x)f(x)12或0xx12f(x)a gx()af(x)g(x)（a1）f(x)减函数：？log a f(x)log a g(x)f(x)0f(x)g(x) （0a1）注：①判断单调性必须考虑定义域②f(x)单调性判断3．基本不等式定义法、图象法、性质法“增+增=增”①a2b22ab ③奇函数在对称区间上单调性相同ab②若a,bR，则ab2 注：用均值不等式ab2ab、abab()22偶函数在对称区间上单调性相反3．周期性T是f(x)周期f(xT)f(x)恒成立（常数T0）求最值条件是“一正二定三相等”4．二次函数解析式：f(x)=ax 2+bx+c，f(x)=a(x-h)2+kf(x)=a(x-x1)(x-x2)对称轴：xb2a2b4acb顶点：(,)2a4anlog a blogbna1logba b单调性：a>0，](,2ab递减，[,)2a递增logN注：性质log a10log a a1aaN常用对数lgNlog10N，lg2lg51当xb2a，f(x)min4 ac4 ab2自然对数NNlnlog，lne1e3．指数与对数函数y=a x与y=logx与y=loga x奇偶性：f(x)=ax 2+bx+c是偶函数b=0闭区间上最值：配方法、图象法、讨论法---注意对称轴与区间的位置关系注：一次函数f(x)=ax+b奇函数b=0定义域、值域、过定点、单调性？x注：y=a与y=log a x图象关于y=x对称（互为反函数）1四、基本初等函数4．幂函数y x2,yx3,yx,yx2,yx3,yx,yx210a 1．指数式a1(0)ann1mmnaanay x在第一象限图象如下：b2．对数式logNbaNa（a>0,a≠1）1010 log a MNlog a Mlog a Nlog MalogMlogNaa Nn log a Mnlog aMlog mmlogbalogb a l g lg bayy五、函数图像与方程y=f(x)y=f(|x|) 1．描点法函数化简→定义域→讨论性质（奇偶、单调）aobcaoxbc x取特殊点如零点、最值点等3．零点定理若f(a)f(b)0，则yf(x)在(a,b)内有零点2．图象变换平移：“左加右减，上正下负”（条件：f(x)在[a,b]上图象连续不间断）yf(x)yf(xh)注：①f(x)零点：f(x)0的实根1每一点的横坐标变为原来的倍伸缩：)yf(x)yf(x ②在[a,b]上连续的单调函数f(x)，f(a)f(b)0 则f(x)在(a,b)上有且仅有一个零点③二分法判断函数零点---f(a)f(b)0？对称：“对称谁，谁不变，对称原点都要变”x轴yf(x)yf(x)六、三角函数y轴yf(x)yf(x)原点yf(x)yf(x) 1．概念第二象限角,2)(2kk(kZ)2注：yf(x) 直线x ayf(2ax)12．弧长lr扇形面积Slr2翻折：yf(x)y|f(x)|保留x轴上方部分，并将下方部分沿x轴翻折到上方3．定义sinyrcosxrtanyx 其中P(x,y)是终边上一点，POryyy=f(x)y=|f(x)|4．符号“一正全、二正弦、三正切、四余弦”5．诱导公式：“奇变偶不变，符号看象限”aocaoxbbcx如Sin(2)sin ，cos(/2)sinyf(x)yf(|x|)保留y 轴右边部分，6．特殊角的三角函数值并将右边部分沿y 轴翻折到左边364322a2b2asinbcosasin()(tan)bsin01222310128．三角函数的图象性质y=sinxy=cosxy=tanxcos13222121tg033 13/0/ 图象7．基本公式sin2tan2同角sincos1cos和差sinsincoscossincoscoscossinsin 单调性：)(,增(0,)减(,)增2222tantan1tant antansinxcosxtanx值域[-1，1][-1，1]无倍角sin22sincoscos2 2sin22cos112sin22cos奇偶奇函数偶函数奇函数tan21 2 tan2tan周期2π2ππ对称轴xk/2xk无降幂cos2α=1 cos22sin21α=cos22中心k,0/2k,0k/2,0叠加)sincos2sin(4注：kZ3sincos2sin() 62、等比数列9．解三角形基本关系：sin(A+B)=sinCcos(A+B)=-cosCa定义：1q(q0)nanABC tan(A+B)=-tanCsincos22absincsin正弦定理：==sinABCa2RsinAa:b:csinA:sin B:s i n C余弦定理：a2=b2+c2－2bccosA（求边）22c2bacosA=（求角）2bcn1通项：aaqn1na(q)1)(q1n求和：Sa(1qqn11)12（a,b,c成等比）中项：bac性质：若mnpq则aaaamnpq 3、数列通项与前n项和的关系面积公式：S△＝12absinC a ns1sna(n1sn1(n1)2)注：ABC中，A+B+C=？ABsinAsinB4、数列求和常用方法2＞b2+c2?∠A＞a 2公式法、裂项法、错位相减法、倒序相加法七、数列八、平面向量1．向量加减三角形法则，平行四边形法则1、等差数列定义：a n1a n d通项：a n a1(n1)d ABAC首尾相接，OBOC=CB共始点BCn(a1a n)1 求和：中项：中点公式：ABAC2ADD是BC中点abcos2．向量数量积ab==x1x2y1y2注：①a,b夹角：00≤θ≤1800≤θ≤1800 Snan(n1)dn122acb（a,b,c成等差）2：若mnpq，则a性质m aaa npq②a,b 同向：abab模： za2b2zzz2 3．基本定理 a 1ee （e 1,e 2不共线--基底）122复平面：复数z 对应的点(a,b) 平行：a//babx 1yxy （b0）2212．复数运算 加减：（a+bi ）±(c+di)=？垂直：abab0x 1x 2y 1y 20模：a ＝22y 2xab(a b )2乘法：（a+bi ）（c+di ）=？ 除法：a cb i di =(a (c b i )(cci)( di di2乘方：1i ，n ii4ki r) )==, r夹角：cosab |a||b |3．合情推理 类比：特殊推出特殊 归纳：特殊推出一般注：①0∥a ②abcabc （结合律）不成立演绎：一般导出特殊（大前题→小前题→结论）4．直接与间接证明综合法：由因导果③abacbc （消去律）不成立比较法：作差—变形—判断—结论 反证法：反设—推理—矛盾—结论 分析法：执果索因九、复数与推理证明分析法书写格式： 要证A 为真，只要证B 为真，即证,,，这只要证C 为真，而已知C 为真，故A 必为真1．复数概念注：常用分析法探索证明途径，综合法写证明过程复数：zabi(a,bR)，实部a、虚部b5．数学归纳法：分类：实数（b0），虚数（b0），复数集C(1)验证当n=1时命题成立,注：z是纯虚数a0，b0(2)假设当n=k(kN*，k1)时命题成立,相等：实、虚部分别相等证明当n=k+1时命题也成立共轭：zabi由(1)(2)知这命题对所有正整数n都成立注：用数学归纳法证题时，两步缺一不可，归纳假设必须使用1、倾斜角范围0,十、直线与圆2yDxEyF2圆一般方程：0x （条件是？）DE圆心,22半径 r224 DEF2斜率ktany y 21 xx 216、直线与圆位置关系注：直线向上方向与x 轴正方向所成的最小正角位置关系相切相交相离 倾斜角为90时，斜率不存在 2、直线方程 几何特征drdrdr点斜式yy 0k(xx 0)，斜截式ykxb代数特征△0△0△0两点式 AxByC0一般式y y 2 y 1 y 1 x x 2 x 1 x1xy ，截距式1ab注：点与圆位置关系222(xaybr 点 0)()Px 0,y 0在圆外注意适用范围：①不含直线 x x7、直线截圆所得弦长②不含垂直x 轴的直线 ③不含垂直坐标轴和过原点的直线22AB2rd3、位置关系（注意条件）平行 k k 且b 1b 2 12垂直4、距离公式 k 1k 21垂直A 1A 2B 1B 20十一、圆锥曲线两点间距离：|AB|=2(x 1x)(yy)2122一、定义 椭圆：|PF 1|+|PF 2|=2a(2a>|F 1F 2|)点到直线距离： d A xByC0022 AB双曲线：|PF 1|-|PF 2|=±2a(0<2a<|F 1F 2|) 抛物线：与定点和定直线距离相等的点轨迹二、标准方程与几何性质（如焦点在x轴）5、圆标准方程：2()22(x a)ybr圆心(a,b)，半径r22xy椭圆1(a>b>0)22ab 十二、矩阵、行列式、算法初步22xy双曲线1(a>0,b>0)22ab十、算法初步中心原点对称轴？焦点F1(c,0)、F2(-c,0)一．程序框图顶点:椭圆(±a,0),(0,±b)，双曲线(±a,0)程序框名称功能范围:椭圆-axa,-byb起止框起始和结束双曲线|x|a，yR输入和输出的信息焦距：椭圆2c（c= 2b2a）输入、输出框赋值、计算双曲线2c（c= 2b2a）处理框判断某一条件是否成立2a、2b:椭圆长轴、短轴长，判断框双曲线实轴、虚轴长离心率：e=c/a椭圆0<e<1,双曲线e>1循环框重复操作以及运算22xyb注：双曲线1渐近线xy22aba2ny2方程mx1表示椭圆m0,n0.mn2ny2方程mx1表示双曲线mn0 二．基本算法语句及格式抛物线y2=2px(p>0)2=2px(p>0)1输入语句：INPUT“提示内容”；变量2输出语句：PRINT“提示内容”；表达式顶点（原点）对称轴（x轴）3赋值语句：变量=表达式开口（向右）范围x0离心率e=1p 焦点,0)F(准线2 xp24条件语句“IF—THEN—ELSE”语句“IF—THEN”语句例1辗转相除法求得123和48最大公约数为3 IF 条件THENIF 条件THEN语句1语句例2已知f(x)=2x 5－5x 4－4x 3+3x 2－6x+7，秦九韶算法求f(5) 123＝2×48＋27v0=2ELSEENDIF48＝1×27＋21v1=2×5－5=5 语句227＝1×21＋6v2=5×5－4=21ENDIF21＝3×6＋3v 3=21×5+3=108 5循环语句6＝2×3+0v4=108×5－6=534当型循环语句直到型循环语句 WHILE 条件DO v5=534×5+7=2677 循环体循环体 WENDLOOPUNTIL 条件当型“先判断后循环”直到型“先循环后判断”十三、立体几何三．算法案例1、求两个数的最大公约数 1．三视图正视图、侧视图、俯视图辗转相除法：到达余数为0 2．直观图：斜二测画法'''0 XOY=45更相减损术：到达减数和差相等平行X 轴的线段，保平行和长度 2、多项式f (x)=a nx n+an-1x n-1+⋯.+a1x+a 0的求值n +an-1x n-1+⋯.+a1x+a 0的求值平行Y 轴的线段，保平行，长度变原来一半 秦九韶算法：v 1=a n x+a n －1v 2=v 1x+a n －23．体积与侧面积 v3=v2x+an －3vn=vn －1x+a0 注：递推公式v 0=anv k =v k－1X+a n －k (k=1,2,⋯n)求f(x)n 值，乘法、加法均最多次V 柱=S 底hV锥=1 3S 底hV 球=4 33πR3、进位制间的转换 S 圆锥侧=rlS 圆台侧=(Rr)lS24R球表=k 进制数转换为十进制数： 4．公理与推论确定一个平面的条件：nn1aa 1.....aa(k)akak.........aka nn10nn110①不共线的三点②一条直线和这直线外一点十进制数转换成k 进制数：“除k 取余法”③两相交直线④两平行直线若两个平面垂直，则一个平面内垂直于交公理：平行于同一条直线的两条直线平行P 定理：如果两个角的两条边分别对应平行，那么这两个角相等或互补。