excel双样本 t检验法的计算方法

Excel 中双样本t 检验之等方差异方差假设成组资料（非配对资料）的t 检验，是生物统计中必须掌握的基本技能贮备之一。

在Excel 完全安装情况下，加载“分析工具库”，之后会在菜单上出现“数据分析”选项，我们会发现“分析工具”中有两个选项，分别是：“t 检验：双样本等方差假设”、“t 检验：双样本异方差假设”。

那么，对于成组资料t 检验，什么时候用等方差，什么时候用异方差呢？最好的办法就是进行“F 检验 双样本方差”齐性检验。

如果通过检验，两个样本方差差异不显著，则选用“t 检验：双样本等方差假设”，如果两样本方差差异显著，则选用“t 检验：双样本异方差假设”。

例：有人曾对公雏鸡作了性激素效应试验。

将22只公雏鸡完全随机地分为两组，每组11只。

一组接受性激素A （睾丸激素）处理；另一组接受激素C （雄甾烯醇酮）处理。

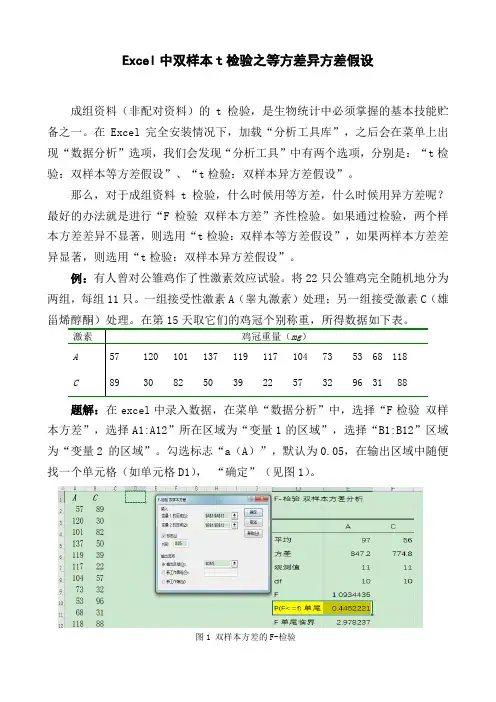
在第15天取它们的鸡冠个别称重，所得数据如下表。

题解：在excel 中录入数据，在菜单“数据分析”中，选择“F 检验 双样本方差”，选择A1:A12”所在区域为“变量1的区域”，选择“B1:B12”区域为“变量2 的区域”。

勾选标志“a （A ）”，默认为0.05，在输出区域中随便找一个单元格（如单元格D1）， “确定”（见图1）。

图1 双样本方差的F-检验图2 t-检验：双样本等方差假设检验 从上图可以看出，p=0.4452221﹥0.05，表示激素A 与激素C 的对应的鸡冠，方差差异不显著。

换言之，就是样本A 与样本B 为等方差，在t 检验时，就选择“t 检验：双样本等方差假设”，得到图2结果。

从图2输出结果可以看出，t检验的结果是p=0.003000143﹤0.01，表明差异极显著。

也就是说，激素A 处理的鸡冠重（97mg ）极显著地高于激素C 处理的鸡冠重（56mg ）。

目前不管是本科教材，还是高职高专教材，生物统计仍是以公式手动计算为主，所采用的基本都是按照“t 检验：双样本等方差假设”，而且很多资料也表示，如果双样本都来源于同一总体，可以采用“t 检验：双样本等方差假设”。

excel双样本t检验法的计算方法摘要：1.Excel双样本T检验的概念与原理2.准备工作：数据准备与输入3.执行双样本T检验：步骤与操作4.解读结果：假设检验与结论5.实际应用案例与注意事项正文：在数据分析和统计研究中，Excel双样本T检验法被广泛应用于比较两组数据的均值是否存在显著差异。

本文将详细介绍Excel双样本T检验的计算方法，包括操作步骤、结果解读以及实际应用案例。

1.Excel双样本T检验的概念与原理双样本T检验是一种统计分析方法，用于检验两个独立样本的均值是否存在显著差异。

它基于t分布理论，通过计算t统计量及其对应的p值来判断假设检验的结果。

2.准备工作：数据准备与输入在进行双样本T检验之前，需要首先准备好两组要分析的数据。

这两组数据可以来自不同来源、不同时间或不同条件下收集。

确保数据具有可比性，例如单位、尺度等要保持一致。

将数据输入Excel，建议将两组数据分别放在两个工作表中，以便于进行数据分析。

通常，第一列表示样本编号或组别，后续列表示各样本的观测值。

3.执行双样本T检验：步骤与操作在Excel中进行双样本T检验，可以遵循以下步骤：步骤1：打开Excel，点击“数据”菜单，选择“数据分析”。

步骤2：在“数据分析”对话框中，选择“t-检验：双样本假设检验”模块。

步骤3：分别选取两组数据所在的工作表和输出区域。

步骤4：点击“确定”，等待Excel计算结果。

4.解读结果：假设检验与结论Excel会输出双样本T检验的结果，包括t统计量、p值以及结论。

根据p 值与预设的显著性水平（通常为0.05）进行比较，可以得出以下结论：- 如果p值小于显著性水平，说明两组数据的均值存在显著差异；- 如果p值大于显著性水平，不能拒绝原假设，即两组数据的均值之间没有显著差异。

5.实际应用案例与注意事项实际应用中，双样本T检验可用于比较不同实验组之间的效果、评估干预措施的有效性等。

在进行双样本T检验时，请注意以下几点：- 确保数据具有可比性，如单位、尺度一致；- 检查数据是否存在异常值，如有需要，进行数据清洗；- 选择合适的显著性水平，根据实际情况调整；- 注意样本容量，确保样本足够大以获得可靠结果。

t检验计算公式t检验是一种用于比较两组数据均值是否有显著差异的统计方法。

在进行t检验之前，我们需要计算 t 值，以判断变量之间是否存在显著差异。

下面将介绍 t 检验的计算公式及步骤。

计算步骤：1. 收集数据：首先，我们需要收集两组数据，分别记为X和Y。

这两组数据可以是实验组和对照组，或者两个不同时间点的观测值等。

2. 计算样本均值：对于每一组数据，计算其样本均值。

记X的样本均值为X，Y的样本均值为Ȳ。

样本均值可以通过求和后除以观测值的个数来得到。

3. 计算样本标准差：计算每一组数据的样本标准差。

记X的样本标准差为sX，Y的样本标准差为sY。

样本标准差可以通过计算每个观测值与均值的差的平方和的平均值，再取平方根得到。

4. 计算自由度：自由度的计算公式为df = n1 + n2 - 2，其中n1和n2分别表示两组数据的观测值个数。

5. 计算标准误差：标准误差的计算公式为SE = sqrt(sX^2/n1 +sY^2/n2)，其中sX和sY分别表示两组数据的样本标准差。

6. 计算 t 值：t 值的计算公式为t = (X - Ȳ) / SE。

7. 查找临界 t 值：根据设定的显著性水平（通常为0.05或0.01），查找 t 分布表，找到与自由度对应的临界 t 值。

比较计算出的 t 值和临界 t 值，以确定是否拒绝原假设。

8. 进行假设检验：根据计算出的 t 值和临界 t 值，进行假设检验。

如果计算得到的 t 值大于临界 t 值，则拒绝原假设，即认为两组数据均值存在显著差异；反之，则接受原假设，即认为两组数据均值无显著差异。

总结：t检验计算公式包括样本均值、样本标准差、自由度、标准误差和t 值的计算。

通过计算出的t值与临界t值进行比较，判断两组数据均值是否存在显著差异。

对于实际应用中的问题，我们可根据t检验的计算公式进行数据分析，从而得出客观准确的结论。

Excel在生物统计学双样本异方差资料t检验中的应用作者：白俊艳杨帅武晓红王旭来源：《现代农业科技》2016年第22期摘要利用Excel对双样本异方差的数据资料进行t检验，并以在pH=5和pH=8条件下测定果蝇的TPI酶活性为案例详细阐述了其分析过程及其注意事项，利用显著性概率P（T≤t）来判定结果更为简单一些。

关键词 Excel；生物统计学；t检验；双样本异方差资料中图分类号 G642.0 文献标识码 A 文章编号 1007-5739（2016）22-0284-01生物统计学是畜牧、兽医、农学、微生物、医学等领域中不可缺少的统计工具，数据分析离不开生物统计学的原理。

随着计算机技术的发展，已有更多的软件被应用于生物统计学，如SPSS[1-4]、Excel[5]、SAS[6]等，但是不同的统计软件有不同的特点，如Excel统计功能虽然简单，但是操作方便，分析出来的结果更为直观，更适合生物统计学的初学者。

1 分析工具库的安装Excel一般并不直接带着“分析工具库”这一模块，需要在Excel的基础上自行安装。

安装步骤：Excel的工具—加载宏—分析工具库—确定。

2 双样本等方差数据资料的t检验一般很难从数据资料上确定2个样本的方差是否相等，需要对其做方差的齐性检验来判断。

下面以果蝇的TPI酶活性为例，阐述双样本异方差的t检验过程。

2.1 数据资料的建立为了比较果蝇中TPI酶活性在pH=5和pH=8时是否有区别，将10只果蝇随机分为2组，一组测定在pH=5下的TPI酶活性，另一组测定在pH=8下的TPI酶活性，问这2种pH值下的平均TPI活性是否有显著差异[7]。

首先在Excel中把分组的名称“pH=5”和“pH=8”分别填入每一列的最上方，然后在“pH=5”和“pH=8”下方录入其果蝇的TPI酶活性数据资料，具体如图1所示。

2.2 t检验分析因为在本数据资料里，没有提到2个总体方差相等还是不相等，因此有必要先对数据资料进行方差齐性检验。

t检验是一种常用的假设检验方法，用于判断样本均值与总体均值之间是否存在显著差异。

在统计学中，t检验常用于比较两个样本均值的差异性，或者判断某个样本均值与已知总体均值之间的关系。

让我们来简单了解一下t检验的原理。

t检验的原理基于样本和总体的均值和方差之间的关系，通过计算t值来判断样本均值与总体均值之间的差异是否显著。

在进行t检验时，我们需要首先计算样本的t值，然后根据自由度和置信水平查表或使用计算模板来确定t临界值，最终比较计算得到的t值和临界值来得出结论。

在实际应用中，我们可以借助Excel等软件来进行t检验的计算。

事实上，Excel提供了丰富的统计函数和计算模板，可以方便地进行t检验的计算和分析。

如果你不熟悉t检验的计算方法，可以使用Excel的内置函数来进行计算，这样可以节省大量的时间和精力，同时也避免了可能的计算错误。

在进行t检验计算时，我们需要提供样本数据、总体均值和显著性水平等参数，然后使用Excel的t检验函数或计算模板来进行计算。

通过这种方式，我们可以快速得到t值和p值等结果，从而进行结果解释和结论推断。

Excel还提供了丰富的图标和表格功能，可以帮助我们直观地展示t检验的结果，进一步提高分析的可视化效果。

t检验是一种重要的统计方法，可以帮助我们判断样本均值与总体均值之间是否存在显著差异。

在实际应用中，借助Excel等软件进行t检验的计算和分析可以帮助我们高效、准确地得出结论，为决策提供科学依据。

希望通过本文的介绍和讨论，你对t检验的计算模板和应用有了更深入的了解。

t检验是一种常用的假设检验方法，用于判断样本均值与总体均值之间是否存在显著差异。

在统计学中，t检验常用于比较两个样本均值的差异性，或者判断某个样本均值与已知总体均值之间的关系。

让我们来简单了解一下t检验的原理。

t检验的原理基于样本和总体的均值和方差之间的关系，通过计算t值来判断样本均值与总体均值之间的差异是否显著。

在进行t检验时，我们需要首先计算样本的t值，然后根据自由度和置信水平查表或使用计算模板来确定t临界值，最终比较计算得到的t值和临界值来得出结论。

实验二利用EXCEL软件进行平均数的t测验
一、实验目的：
1．巩固成组资料t测验及其区间估计的方法与步骤。

2．巩固成对资料t测验及其区间估计的方法与步骤。

3．熟练掌握Excel数据分析中“数据分析”工具使用方法与技能。

二、原理与步骤：
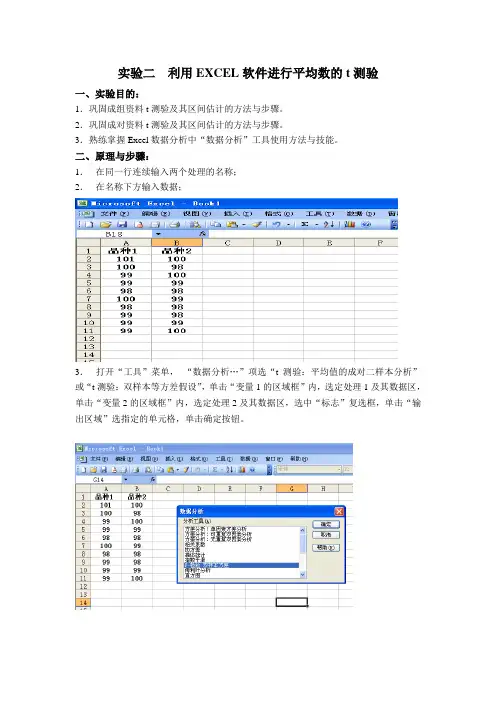
1．在同一行连续输入两个处理的名称；
2．在名称下方输入数据；
3．打开“工具”菜单，“数据分析…”项选“t测验：平均值的成对二样本分析”或“t测验：双样本等方差假设”，单击“变量1的区域框”内，选定处理1及其数据区，单击“变量2的区域框”内，选定处理2及其数据区，选中“标志”复选框，单击“输出区域”选指定的单元格，单击确定按钮。

4．输出结果判读、区间估计、作结论。

三、数据资料：
1．可用书中例题中的数据资料，作为验证性试验。

2．数据资料：
四、实验方式与分组要求：
一人一组，一人一台计算机。

五、作业：
使用Excel数据分析计算。

作t检验或成对t检验，并比较两种分析结果的异同，指出正确的分析方法，并解释为什么它是正确的分析方法。

t检验的公式t检验是一种常用的统计方法，用于比较两个样本的均值是否存在显著差异。

它是由英国统计学家William Sealy Gosset于1908年发表的，因为他在Guinness酒厂工作，所以以“学生”为笔名，称之为“学生t检验”。

t检验的公式如下：t = (x1 - x2) / sqrt(s1^2/n1 + s2^2/n2)其中，x1和x2分别表示两个样本的均值，s1和s2分别表示两个样本的标准差，n1和n2分别表示两个样本的样本量。

t值的绝对值越大，表示两个样本均值差异越显著。

在实际应用中，t检验常用于以下几个方面：1. 假设检验：t检验可以帮助我们判断两个样本的均值是否存在显著差异。

通过设定显著性水平（一般为0.05），当t值的绝对值大于临界值时（临界值可查t分布表得到），就可以拒绝原假设，认为两个样本的均值存在显著差异。

2. 置信区间估计：t检验可以用来估计两个样本均值的差异范围。

通过计算置信区间，可以得到均值差异的一个范围估计，从而对差异的大小进行评估。

3. 样本量确定：t检验可以帮助我们确定合适的样本量。

通过给定显著性水平、效应大小和统计功效，可以计算出需要的样本量，从而在实际研究中提供参考。

4. 相依样本的比较：除了比较独立样本的均值差异外，t检验还可以用于比较相依样本（如前后测量、配对样本）的差异。

相依样本的t检验是通过计算差值的均值和标准差来判断差异是否显著。

需要注意的是，在使用t检验时，需要满足以下前提条件：1. 总体分布近似正态分布：t检验基于正态分布的假设，因此样本数据应该近似服从正态分布。

如果数据不服从正态分布，可以考虑进行数据转换或使用非参数检验方法。

2. 样本独立性：两个样本应该是相互独立的，即一个样本的观测值不受另一个样本观测值的影响。

3. 方差齐性：两个样本的方差应该相等。

如果两个样本的方差差异较大，可以使用修正的t检验方法。

t检验是一种常用且实用的统计方法，可以帮助我们比较两个样本的均值差异。

利用Excel进行t检验分析在科学研究中，经常要对收集到的数据进行各种统计分析，而分析数据时，大多使用较著名的统计分析软件包，如SAS、SPSS等。

这些统计分析软件包功能强大，不仅能单变量分析，而且可做各种复杂的多变量分析。

然而，在对数据进行处理时，大多是使用简单统计描述，制作各种统计图表，或者进行t检验、方差分析、相关分析及回归分析。

作这些统计分析时，大多可使用Windows自带的Excel。

Excel是一种使用极方便的电子表格软件，它有强大的数据管理功能，能制作各种统计图表，具有丰富的财会和统计函数，并且在“分析工具库”中，提供了一组数据分析工具。

使用这些分析工具时，只需指出数据所在的单元格和提供必要的参数，该工具就会使用适宜的统计或工程函数，对数据做处理，给出相应的结果。

有些工具在输出时还能产生图表。

单击“工具”菜单中的“数据分析”命令，可以浏览已有的分析工具。

如果在“工具”菜单上没有“数据分析”命令，应在“工具”菜单上运行“加载宏”命令，在“加载宏”对话框中选择“分析工具库”。

在进行两个样本均值相等假设分析时，可使用t-检验分析，根据情况选择：成对双样本均值分析、双样本等方差假设分析和双样本异方差假设分析。

1.t-检验：成对双样本均值分析当样本中的观察值存在配对关系时，可以使用“成对双样本t-检验”。

例如对一个样本组在实验前后进行了2次检测，为确定实验前后样本均值是否相等，应使用成对t检验，此t-检验并不假设两个总体的方差是相等的。

例如，用克矽平治疗矽肺患者10例，治疗前后血红蛋白含量如下：治疗前113 150 150 135 128 100 110 120 130 123治疗后140 138 140 135 135 120 147 114 138 120在工作表中输入上面的数据，比如数据区为A1至K2。

分析时，在“工具”菜单中，单击“数据分析”命令。

在数据分析对话框中，选择t-检验：成对双样本均值分析，拉出成对双样本均值分析对话框，其中有如下输入项(其他分析工具对话框内容和用法与之相似)：变量1的区域：输入需要分析的第一个数据区域的单元格引用。

excel2007使用t检验的方法步骤详解excel2007使用t检验的方法步骤详解excel2007使用t检验的方法T检验步骤1：点击fx，类别选统计，找到TTEST。

excel2007使用t检验的方法图1excel2007使用t检验的方法图2T检验步骤2：Array1,2分别选择要进行检验的两组数值，Tails一般填2(双尾检验);Type填1就是配对t检验，填2就是等方差双样本检验，填3就是异方差双样本检验。

T检验步骤3：不懂的话，可以看填参数对话框下面的有关该函数的帮助excel2007使用t检验的方法图3在EXCEL中如何把B列与A列不同之处标识出来(一)、如果是要求A、B两列的同一行数据相比较：假定第一行为表头，单击A2单元格，点格式- 条件格式，将条件设为:单元格数值不等于=B2点格式- 字体- 颜色，选中红色，点两次确定。

用格式刷将A2单元格的条件格式向下复制。

B列可参照此方法设置。

(二)、如果是A列与B列整体比较(即相同数据不在同一行)：假定第一行为表头，单击A2单元格，点格式- 条件格式，将条件设为:公式=COUNTIF($B:$B,$A2)=0点格式- 字体- 颜色，选中红色，点两次确定。

用格式刷将A2单元格的条件格式向下复制。

B列可参照此方法设置。

按以上方法设置后，AB列均有的数据不着色，A列有B 列无或者B列有A列无的数据标记为红色字体。

EXCEL中怎样批量地处理按行排序假定有大量的数据(数值)，需要将每一行按从大到小排序，如何操作?由于按行排序与按列排序都是只能有一个主关键字,主关键字相同时才能按次关键字排序。

所以，这一问题不能用排序来解决。

解决方法如下：1、假定你的数据在A至E列，请在F1单元格输入公式：=LARGE($A1:$E1,COLUMN(A1))用填充柄将公式向右向下复制到相应范围。

你原有数据将按行从大到小排序出现在F至J列。

如有需要可用选择性粘贴/数值复制到其他地方。