第10章 达朗贝尔原理—习题(1-16)

129第十章 量子物理基础本章提要1． 光的量子性· 物体由于自身具有一定温度而以电磁波的形式向周围发射能量的现象称热辐射。

· 在任何温度下都能全部吸收照射到其表面上的各种波长的光（电磁波），的物体称为绝对黑体，简称黑体。

· 单位时间内从物体单位表面积发出的、波长在λ附近单位波长间隔内电磁波的能量称单色辐射本领（又称单色辐出度），用)(T M λ表示· 单位时间内物体单位表面积发出的包括所有波长在内的电磁波的辐射功率称为辐射出射度，用则M 表示，M 与)(T M λ的关系为0()d M M T λλ∞=⎰2． 维恩位移定律在不同的热力学温度T 下，单色辐射本领的实验曲线存在一个峰值波长λm ， T 和λm 满足如下关系：λm T b =其中，b 是维恩常量。

该式称维恩位移定律。

3． 斯忒藩—玻尔兹曼定律· 黑体的辐射出射度M 与温度T 的关系为4T M σ=其中，σ为斯忒藩—玻尔兹曼常量。

该结果称斯忒藩—玻尔兹曼定律。

· 对于一般的物体4T M εσ=ε称发射率。

4． 黑体辐射· 能量子假说：黑体辐射不是连续地辐射能量，而是一份份地辐射能量，并且每一份能量与电磁波的频率ν成正比，满足条件E nhv =，其中n ＝1，2，3，…，等正整数，h 为普朗克常数。

这种能量分立的概念被称为能量量子化，130每一份最小的能量E hv =称为一个能量子。

· 普朗克黑体辐射公式（简称普朗克公式）为112)(/52-=kT hc e hc T M λλλπ其中，h 是普朗克常量。

由普朗克公式可以很好地解释黑体辐射现象。

· 光子假说：光是以光速运动的粒子流，这些粒子称为光量子，简称光子。

一个光子具有的能量为νh E =动量为 λh p =5． 粒子的波动性· 实物粒子也具有波粒二象性，它的能量E 、动量p 与和它相联系的波的频率ν、波长λ满足关系2E mc h ν==λh p m u == 这两个公式称为德布罗意公式或德布罗意假设。

达朗贝尔原理一、是非题1. 在使用动静法时，凡是运动着的质点都应加上惯性力。

（ ⨯ ）2. 通过刚体上O 点的三根相互垂直的坐标轴，如果满足：J XY = J ZX =0，J XY = J YZ =0，则O X ，O Y ，O Z 一定是O 点的三根惯性主轴。

（ √ ）3. 平动刚体惯性力系可简化为一个合力，该合力一定作用在刚体的质心上。

（ √ ）4. 具有垂直于转轴的质量对称面的转动刚体，其惯性力系可简化为一个通过转轴的力和一个力偶，其中力偶的矩等于对转轴的转动惯量与刚体角加速度的乘积，转向与角加速度相反。

（ √ ）5. 应用达朗伯原理时，在质点系的每一质点上加上惯性力F gi 后，作用于每一质点的主动力F i 、约束力F N i ，与惯性力F gi 成平衡，即F i + F N i + F gi =0，因此，只须写出方程∑F i +∑F N i + ∑F gi =0即可求解。

（ ⨯ ）6. 平面运动刚体上惯性力系的合力必作用在刚体的质心上。

7. 刚体作定轴转动时，如果质心正好在其转动轴上，则附加动反力为零。

（ × ）8. 质点系达朗贝尔原理在空间力系问题中的六个平衡方程可写为：∑=0x F ，∑=0y F ，∑=0z F ，∑=0x M ，∑=0y M ，∑=0z M 。

是否可写为：A. 四投影二矩的形式（ × ）B. 四矩二投影的形式（ √ ）C. 五矩一投影的形式（ √ ）D.六矩的形式（ √ ） 9. 平面运动刚体惯性力系主矢的方向与质心加速度的方向相反，而主矩的转向与刚体的角加速度方向一致。

（ × ）10. 质点的达朗贝尔原理为0g N =++F F F ，对由n 个质点组成的质点系，将上式求和，有0)(1g N =++∑=n i i i iF F F ，这就是质点系的达朗贝尔原理，对吗？（ × ）11. 无论刚体作何运动，其惯性力系主矢都可由C m F a -=gR 确定吗？（gR F 为惯性力系主矢，m 为刚体总质量，C a 为质心加速度）（ √ ）。

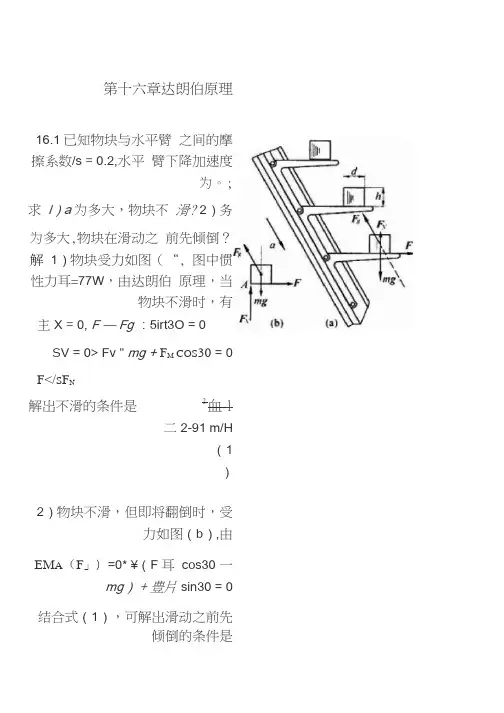
第十六章达朗伯原理16.1已知物块与水平臂之间的摩擦系数/s = 0.2,水平臂下降加速度为。

; 求l）a为多大，物块不滑? 2）务为多大,物块在滑动之前先倾倒？解1）物块受力如图（“, 图中惯性力耳=77W，由达朗伯原理，当物块不滑时，有主X = 0, F —Fg：5irt3O = 0SV = 0> Fv " mg + F M COS30 = 0 F</S F N解岀不滑的条件是2血l二2-91 m/H（1）2）物块不滑，但即将翻倒时，受力如图（b）,由EM A（F」）=0* ¥（F耳cos30 一mg）+ 豊片 sin30 = 0结合式（1），可解岀滑动之前先倾倒的条件是h、1 孑鼻泾E6.2已知曲柄OC = rM匀角速度如转动;连杆召C = I端连有质量为櫛的物A ;求杆AB所受的力。

解设杆长AB =趴则物A 的运动方程为j ： = b + r cos 爷 + I cos®cos® 1 — -y ^2 sin 2 卩j- = 6 + r cos 护 + I1 r2 . 2-2 7 s,n由达朗伯原理 SX = 0, mg - F - F* = 0得 AH 杆的力 F = 7ti[g + nw 2( cc^<p * y CQS 2^P )], 式中 ip — (Ait16.3已知 半径为『的圆轮对轴O 的转动惯量为丿*轮上 作用有恒力偶矩M 、轮缘上的销子C 推动质量为丹的滑槽ABD 沿水平滑道运动，滑道处摩擦系数为/ ■其余各处光滑；求 圆轮的转动微分方程。

解如图冷），圜盘角加速度为盘=花滑槽的运动方程和加 速度为J" = r COS 护， X = _ F （护2 8S 卩 + 0 审口爭）圆轮受力如图（b ）,图中惯性力偶距皿0 =北=宛•由达朗伯原式中 cosB 二 J 1 -尹 sin* <p物块受力如图（b ）,图中惯性力F 厂w(b)题16.3图乞Mo(F) = 0, A4 —- F.\r sin^j = 0得出J<p + F\r或1呻=M (1) 滑槽受力如图c、图中惯性力F f=豳，由达朗伯原理至X ~ 0* —P\ Fg l (F[ + F?) —0SY = 0, Fyp + F\i2 ~wg = 0 也及Fl =fFy；i, F2= JV池、Fy 二F、r 可得Fyj = Fv — ~ r>^ + fmg将式(2)代入式(1),得轮子的运动微分方程(J + mr~ sin2c：)G： + mr^ cos誓対口炉•炉'+ 6nijr sine? = M16.4已知物E质量m\ - 2 000 kg,物B质量酬2 =kg,物B下绳子拉力F r - 3 kN，不计滑轮的质量；求物E的加速度◎和绳FD的张力F HJC 解设物E*物B加速度如图*则a fl= 2a ;轮0和物E系统的受力.图中F曲=叱购=2叫;设轮O半径为厂2 .由达朗怕原理得SM Q( F) = 0, F( r；+ F测2「^1^2 什焜前2 =() ⑴轮C和物E系统的受力图中件=^2g, F；= Fi°设轮C半径为n，由达朗伯原理EM C(F)二0,_ *Fi厂I - F H Z I = 0SY = 0,F\ + F FD - mig - Eg = 0 (2) 由式(1)、(2)和其它各式，懈出一2丹七2如厂瞬“④讹/ni] +FfD^lg +-Wj-- = 10+21 kN16.5已知车重心为G,加速度为血’以及尺寸6f e t h ;求前后轮的压力；又，“为多大，方可使前后轮压力相等匸解设车质量为砒、受力如图，图中Fg = ma, P = mg 由达朗伯原理EM B(F) —0, (b+ c)F\x - 6P + hF K= 0SM A(F)= 0, -(b +CF.w + cP + = 0題込.4图4/2816.6已知曲杆线密度为宀圆弧半径为尸，以匀角速度绕轴O 转动，不计璽力，图(&)*求任意載面B处对AB段的约束反力。

可编辑修改精选全文完整版机械原理第十章习题一、单项选择题1.渐开线齿轮的齿廓曲线形状取决于( )A.分度圆B.齿顶圆C.齿根圆D.基圆2.计算蜗杆传动的传动比时，公式( )是错误的。

A. i=ω1/ω2B. i=n1/n2C. i=d2/d1D. i=Z2/Z13.在安装标准直齿轮时若中心距大于标准中心距，则将使( )A.重合度变大B.定角速比无法保证C.啮合角变大D.节圆压力角变小4. 单个渐开线齿轮（）A．分度圆等于节圆B．分度圆小于节圆C．分度圆大于节圆D．没有节圆5. 蜗轮的螺旋角β与蜗杆（）A．分度圆处的导程角γ大小相等，方向相反B．B．分度圆处的导程角γ大小相等，方向相同C．齿顶圆处的导程角γ1大小相等，方向相反D.齿顶圆处的导程角γ1大小相等，方向相同6.为了减少蜗轮刀具数目，有利于刀具标准化，规定（）为标准值。

A.蜗轮齿数B.蜗轮分度圆直径C.蜗杆头数D.蜗杆分度圆直径7. 渐开线齿轮的齿根圆（）A．总是小于基圆 B．总是等于基圆C．总是大于基圆 D．有时小于基圆，有时大于基圆8. 为了实现两根相交轴之间的传动，可以采用（）A．蜗杆传动B．斜齿圆柱齿轮传动C．直齿锥齿轮传动D．直齿圆柱齿轮传动9. 一对标准齿轮啮合传动时，其啮合角（）其分度圆压力角。

A.大于B.等于C.小于D.可能等于也可能大于10.用齿条刀具加工渐开线齿轮时，判断被加工齿轮产生根切的依据是（）。

A.刀具的齿顶线通过啮合极限点N1B.刀具的齿顶线超过啮合极限点N1C.刀具的中线超过啮合极限点N1D.刀具的中线不超过啮合极限点N111.在设计计算单个渐开线齿轮的几何尺寸时的基准圆是（）A.基圆B.齿根圆C.分度圆D.齿顶圆12. 一对正确啮合的斜齿圆柱齿轮传动的( )均为标准值。

A．法面模数、分度圆上的法面压力角B．端面模数、分度圆上的端面压力角C．端面模数、分度圆上的端面压力角、分度圆上的螺旋角D．法面模数、分度圆上的法面压力角、分度圆上的螺旋角13. 常用来传递空间两交错轴运动的齿轮机构是( )A.直齿圆柱齿轮B.直齿圆锥齿轮C.斜齿圆锥齿轮D.蜗轮蜗杆14.当一对渐开线齿轮制成后，即使两轮的中心距稍有改变，其传动比仍保持不变的原因是（）A．压力角不变B．啮合角不变 C．节圆半径不变D．基圆半径不变15．渐开线标准齿轮的根切现象发生在（）A．齿数较少时B．模数较小时C．模数较大时D．齿数较多时16．标准直齿圆锥齿轮的标准模数是（）A．大端模数B．小端模数C．平均模数D．求出平均模数后圆整所得的模数17.渐开线齿轮的齿廓曲线形状取决于( )A.分度圆B.齿顶圆C.齿根圆D.基圆18.在安装标准直齿轮时若中心距大于标准中心距，则将使( )A.重合度变大B.定角速比无法保证C.啮合角变大D.节圆压力角变小19.单个渐开线齿轮（）A．分度圆等于节圆B．分度圆小于节圆C．分度圆大于节圆D．没有节圆20.常用来传递空间两交错轴运动的齿轮机构是( )A.直齿圆柱齿轮B.直齿圆锥齿轮C.斜齿圆锥齿轮D.蜗轮蜗杆二、填空题1. 为了不产生过大的轴向力，在斜齿轮的基本参数中，___________不宜过大。

第10章 达朗贝尔原理——习题1-1610-1 均质细直杆AB 通过两根绳索挂在天花板上，已知杆的质量为m ，AB = O 1O 2 = O 1A = O 2B = l ，点C 为杆AB 的质心，绳索O 1A 的角速度为ω，角加速度为α，转向如图所示。

试求图示位置的达朗贝尔惯性力系分别向C ，A 两点的简化结果。

（题10.1答案：）10-2 均质细直杆AB 的质量为m ，长度为l ，绕O 轴作定轴转动，已知OA = l /3，杆的角速度、角加速度分别为ω、α，转向如图所示，试求其达朗贝尔惯性力系分别向质心C 和O 的简化结果。

（题10.2答案：）10-3 质量为mAB ，其两端与半径为r 的半圆形固定凹槽相接触，在图示位置，其角速度为ω，角加速度为α，转向都为顺时针，试求其达朗贝尔惯性力系分别向质心C 和圆心O 的简化结果。

（题10.3答案：）10-4 质量为m ，长度为2l 的均质细直杆AB 的两端分别沿水平地面和铅垂墙面运动，已知v A = 常矢，试求图示位置杆的达朗贝尔惯性力系分别向质心C 和点A 的简化结果。

题10-1图BC题10-2图A（题10.4答案：）10-5 均质杆AB 的质量为m ，长度为l ，用两根等长的绳索悬挂如图。

试求绳索OA 突然被剪断，杆开始运动的瞬时，绳索OB 的张力和杆AB 的角加速度。

（题10.5答案：）10-6 如图所示，质量为m ，长度为l 的均质杆由两根刚度系数为k ，质量不计的弹簧静止悬挂在空中，若突然将右边弹簧剪断，试求剪断瞬时杆AB 的角加速度和点A 的加速度。

（题10.6答案：）10-7 质量为m ，长度为2r 的均质杆AB 的一端A 焊接于质量为m ，半径为r 的均质圆盘的边缘上，圆盘可绕过圆盘中心的光滑水平轴O 转动，若在图示瞬间圆盘的角速度为ω，试求该瞬时圆盘的角加速度及杆AB 在焊接处所受到的约束力。

（题10.7答案：）题10-3图题10-4图题10-5图B题10-6图10-8 固连在一起的两轮子半径分别为r 、R ，它们的总质量为m 1，共同轮心C 为它们的质心，它们对过质心且垂直于纸面的轴的回转半径为ρ。

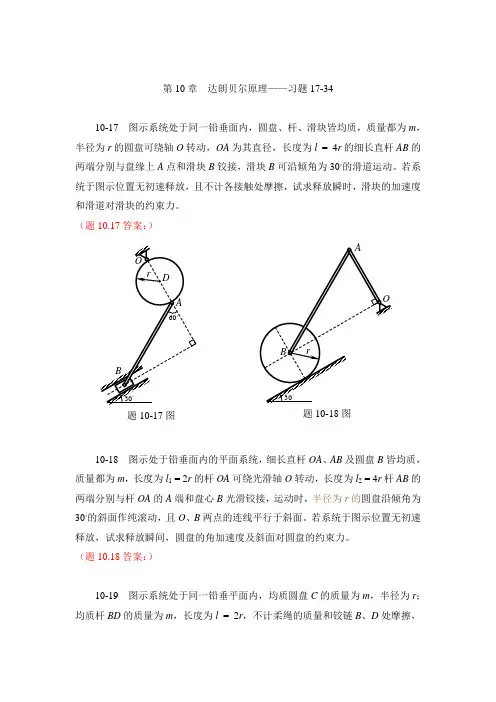
第10章 达朗贝尔原理——习题17-3410-17 图示系统处于同一铅垂面内，圆盘、杆、滑块皆均质，质量都为m ，半径为r 的圆盘可绕轴O 转动，OA 为其直径，长度为l = 4r 的细长直杆AB 的两端分别与盘缘上A 点和滑块B 铰接，滑块B 可沿倾角为30◦的滑道运动。

若系统于图示位置无初速释放，且不计各接触处摩擦，试求释放瞬时，滑块的加速度和滑道对滑块的约束力。

（题10.17答案：）10-18 图示处于铅垂面内的平面系统，细长直杆OA 、AB 及圆盘B 皆均质，质量都为m ，长度为l 1 = 2r 的杆OA 可绕光滑轴O 转动，长度为l 2 = 4r 杆AB 的两端分别与杆OA 的A 端和盘心B 光滑铰接，运动时，半径为r 的圆盘沿倾角为30◦的斜面作纯滚动，且O 、B 两点的连线平行于斜面。

若系统于图示位置无初速释放，试求释放瞬间，圆盘的角加速度及斜面对圆盘的约束力。

（题10.18答案：）10-19 图示系统处于同一铅垂平面内，均质圆盘C 的质量为m ，半径为r ；均质杆BD 的质量为m ，长度为l = 2r ，不计柔绳的质量和铰链B 、D 处摩擦，题10-17图题10-18图若系统于图示位置无初速释放，试求释放瞬时：（1）圆盘的角加速度；（2）柔绳的张力。

（题10.19答案：）10-20 图示系统处于同一铅垂平面内，均质圆盘的质量为m ，半径为r ；杆OD 的质量也为m ，质心C 离转轴O 的距离为3r /2，对转轴O 的回转半径为r 3=ρ；固连于圆盘B 边缘不计质量的销钉A 放置于杆的直槽内，直槽和轴承皆光滑。

已知运动时圆盘能沿水平地面作纯滚动，若系统于图示位置无初速释放，试求释放瞬时：（1）圆盘的角加速度；（2）地面对圆盘的摩擦力。

（题10.20答案：）10-21 图示系统处于同一铅垂平面内，均质杆OA 的质量为m ，长度为l = 2r ；均质圆盘D 的质量为m ，半径为r ；若不计铰链O 、A 处摩擦，系统于图示位置无初速释放，试求释放瞬时两刚体的角加速度。