大学理论力学十达朗贝尔原理答案

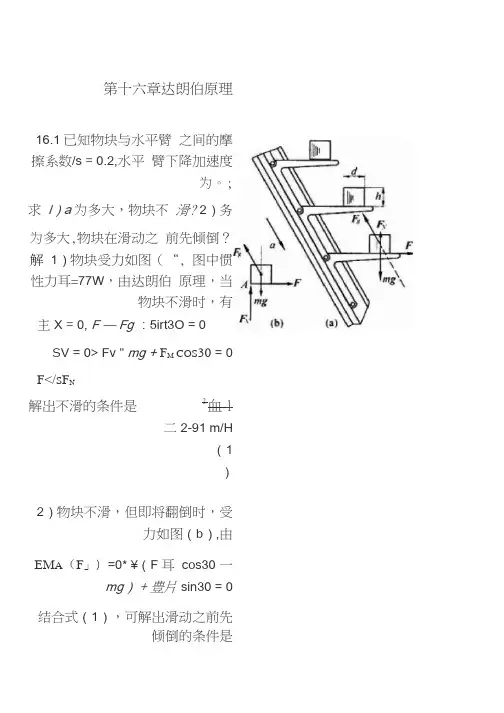
第十六章达朗伯原理16.1已知物块与水平臂之间的摩擦系数/s = 0.2,水平臂下降加速度为。

; 求l）a为多大，物块不滑? 2）务为多大,物块在滑动之前先倾倒？解1）物块受力如图（“, 图中惯性力耳=77W，由达朗伯原理，当物块不滑时，有主X = 0, F —Fg：5irt3O = 0SV = 0> Fv " mg + F M COS30 = 0 F</S F N解岀不滑的条件是2血l二2-91 m/H（1）2）物块不滑，但即将翻倒时，受力如图（b）,由EM A（F」）=0* ¥（F耳cos30 一mg）+ 豊片 sin30 = 0结合式（1），可解岀滑动之前先倾倒的条件是h、1 孑鼻泾E6.2已知曲柄OC = rM匀角速度如转动;连杆召C = I端连有质量为櫛的物A ;求杆AB所受的力。

解设杆长AB =趴则物A 的运动方程为j ： = b + r cos 爷 + I cos®cos® 1 — -y ^2 sin 2 卩j- = 6 + r cos 护 + I1 r2 . 2-2 7 s,n由达朗伯原理 SX = 0, mg - F - F* = 0得 AH 杆的力 F = 7ti[g + nw 2( cc^<p * y CQS 2^P )], 式中 ip — (Ait16.3已知 半径为『的圆轮对轴O 的转动惯量为丿*轮上 作用有恒力偶矩M 、轮缘上的销子C 推动质量为丹的滑槽ABD 沿水平滑道运动，滑道处摩擦系数为/ ■其余各处光滑；求 圆轮的转动微分方程。

解如图冷），圜盘角加速度为盘=花滑槽的运动方程和加 速度为J" = r COS 护， X = _ F （护2 8S 卩 + 0 审口爭）圆轮受力如图（b ）,图中惯性力偶距皿0 =北=宛•由达朗伯原式中 cosB 二 J 1 -尹 sin* <p物块受力如图（b ）,图中惯性力F 厂w(b)题16.3图乞Mo(F) = 0, A4 —- F.\r sin^j = 0得出J<p + F\r或1呻=M (1) 滑槽受力如图c、图中惯性力F f=豳，由达朗伯原理至X ~ 0* —P\ Fg l (F[ + F?) —0SY = 0, Fyp + F\i2 ~wg = 0 也及Fl =fFy；i, F2= JV池、Fy 二F、r 可得Fyj = Fv — ~ r>^ + fmg将式(2)代入式(1),得轮子的运动微分方程(J + mr~ sin2c：)G： + mr^ cos誓対口炉•炉'+ 6nijr sine? = M16.4已知物E质量m\ - 2 000 kg,物B质量酬2 =kg,物B下绳子拉力F r - 3 kN，不计滑轮的质量；求物E的加速度◎和绳FD的张力F HJC 解设物E*物B加速度如图*则a fl= 2a ;轮0和物E系统的受力.图中F曲=叱购=2叫;设轮O半径为厂2 .由达朗怕原理得SM Q( F) = 0, F( r；+ F测2「^1^2 什焜前2 =() ⑴轮C和物E系统的受力图中件=^2g, F；= Fi°设轮C半径为n，由达朗伯原理EM C(F)二0,_ *Fi厂I - F H Z I = 0SY = 0,F\ + F FD - mig - Eg = 0 (2) 由式(1)、(2)和其它各式，懈出一2丹七2如厂瞬“④讹/ni] +FfD^lg +-Wj-- = 10+21 kN16.5已知车重心为G,加速度为血’以及尺寸6f e t h ;求前后轮的压力；又，“为多大，方可使前后轮压力相等匸解设车质量为砒、受力如图，图中Fg = ma, P = mg 由达朗伯原理EM B(F) —0, (b+ c)F\x - 6P + hF K= 0SM A(F)= 0, -(b +CF.w + cP + = 0題込.4图4/2816.6已知曲杆线密度为宀圆弧半径为尸，以匀角速度绕轴O 转动，不计璽力，图(&)*求任意載面B处对AB段的约束反力。

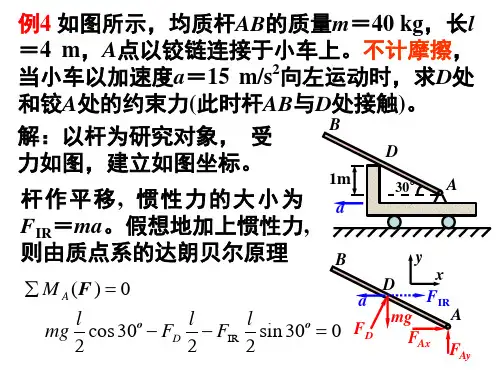
第10章 达朗贝尔原理——习题1-1610-1 均质细直杆AB 通过两根绳索挂在天花板上，已知杆的质量为m ，AB = O 1O 2 = O 1A = O 2B = l ，点C 为杆AB 的质心，绳索O 1A 的角速度为ω，角加速度为α，转向如图所示。

试求图示位置的达朗贝尔惯性力系分别向C ，A 两点的简化结果。

（题10.1答案：）10-2 均质细直杆AB 的质量为m ，长度为l ，绕O 轴作定轴转动，已知OA = l /3，杆的角速度、角加速度分别为ω、α，转向如图所示，试求其达朗贝尔惯性力系分别向质心C 和O 的简化结果。

（题10.2答案：）10-3 质量为mAB ，其两端与半径为r 的半圆形固定凹槽相接触，在图示位置，其角速度为ω，角加速度为α，转向都为顺时针，试求其达朗贝尔惯性力系分别向质心C 和圆心O 的简化结果。

（题10.3答案：）10-4 质量为m ，长度为2l 的均质细直杆AB 的两端分别沿水平地面和铅垂墙面运动，已知v A = 常矢，试求图示位置杆的达朗贝尔惯性力系分别向质心C 和点A 的简化结果。

题10-1图BC题10-2图A（题10.4答案：）10-5 均质杆AB 的质量为m ，长度为l ，用两根等长的绳索悬挂如图。

试求绳索OA 突然被剪断，杆开始运动的瞬时，绳索OB 的张力和杆AB 的角加速度。

（题10.5答案：）10-6 如图所示，质量为m ，长度为l 的均质杆由两根刚度系数为k ，质量不计的弹簧静止悬挂在空中，若突然将右边弹簧剪断，试求剪断瞬时杆AB 的角加速度和点A 的加速度。

（题10.6答案：）10-7 质量为m ，长度为2r 的均质杆AB 的一端A 焊接于质量为m ，半径为r 的均质圆盘的边缘上，圆盘可绕过圆盘中心的光滑水平轴O 转动，若在图示瞬间圆盘的角速度为ω，试求该瞬时圆盘的角加速度及杆AB 在焊接处所受到的约束力。

（题10.7答案：）题10-3图题10-4图题10-5图B题10-6图10-8 固连在一起的两轮子半径分别为r 、R ，它们的总质量为m 1，共同轮心C 为它们的质心，它们对过质心且垂直于纸面的轴的回转半径为ρ。

第13章作业答案
1、解 取圆柱形零件为研究对象，作受力分析，并虚加上零件的惯性力F I。

（1）零件不滑动时，受力如图b 所示，它满足以下条件：
（2）零件不滑动而倾倒时，约束力F N 已集中到左侧点A ，如图c 所示，零件在惯性力作用下将向左倾倒。

倾倒条件是
2、解 取车与矩形块为研究对象如图b 所示。

惯性力为
取矩形块为研究对象，如图c 所示，且矩形块惯性力为
由动静法，不翻倒的条件为
取物块为研究对象，惯性力如图3d 所示。

由动静法
3、解 取平板为研究对象，突然撤去销B 的瞬时平板的角速度ω =0，角加速度α ≠ 0。

平板对质心C 的转动惯量为
平板对A 的转动惯量为
把惯性力系向销A 简化（见图b）得
4、解 取2 球及杆CD 为研究对象如图b 所示，由动静法
5、解 忽略重力影响，惯性力F IC 作功
6、解 取整个系统为研究对象，受力如图b 所示。

因为转速n = 常量，所以角加速度α = 0，惯性力偶矩M I = 0。

（a ）习题11－1图第11章 达朗贝尔原理及其应用11－1 均质圆盘作定轴转动，其中图（a ），图（c ）的转动角速度为常数，而图（b ），图（d ）的角速度不为常量。

试对图示四种情形进行惯性力的简化。

解：设圆盘的质量为m ，半径为r ，则如习题11-1解图：（a ）2I ωmr F =，0I =O M（b ）2n I ωmr F =，αmr F =tI ，αα2I 23mr J M O O == （c ）0I =F ，0I =O M （d ）0I =F ，αα2I 21mr J M O O ==11－2矩形均质平板尺寸如图，质量27kg ，由两个销子 A 、B 悬挂。

若突然撤去销子B ，求在撤去的瞬时平板的角加 速度和销子A 的约束力。

解：如图（a ）：设平板的质量为m ，长和宽分别为a 、b 。

αα375.3I =⋅=AC m Fααα5625.0])(121[222I =⋅++==AC m b a m J M A A∑=0)(F AM ；01.0I =-mg M A ；2rad/s 04.47=α ∑=0x F ；0sin I =-Ax F F θ；其中：6.053sin ==θN 26.956.004.47375.3=⨯⨯=Ax F∑=0y F ；0cos I =-+mg F F Ay θ；8.054sin ==θ习题11－2图习题11-1解图（a ）（a ）N 6.1378.004.47375.38.927=⨯⨯-⨯=Ay F11－3在均质直角构件ABC 中，AB 、BC 两部分的质量各为3.0kg ，用连杆AD 、DE 以及绳子AE 保持在图示位置。

若突然剪断绳子，求此瞬时连杆AD 、BE 所受的力。

连杆的质量忽略不计，已知l = 1.0m ，φ = 30º。

解：如图（a ）：设AB 、BC 两部分的质量各为m = 3.0kg 。

直角构件ABC 作平移，其加速度为a = a A ，质心在O 处。

实验3 刚性转子动平衡实验一、实验目的1．掌握刚性转子动平衡的基本原理和步骤。

2．掌握虚拟基频检测仪和相关测试仪器的使用。

3．熟悉动静法的工程应用。

二、实验性质设计性实验。

三、实验装置（图1）1．动平衡机2．电涡流传感器3．前置器4．接线盒5．调速器6．电子天平7．配重8．微型计算机四、实验背景与基本原理工程中许多高速转动的机器：气轮机、发电机、电动机、陀螺马达等其转子都不是理想的对称刚体，在轴承上安装时也存在着误差（既有偏心又有偏角）。

所以工作时会产生不平衡的惯性力系，引起很大的轴承动约束力。

这种交变的动约束力可引起轴承支座和转轴本身的强烈振动，从而影响机器的工作性能和工作寿命。

消除动约束力的方法是对转子进行动平衡，即通过在转子上适当的地方附加（或除去）小块质量，用其产生的惯性力去平衡原来不平衡的惯性力系，使转轴成为有一定精度的中心惯性主轴。

本实验采用两平面影响系数法对一多圆盘刚性转子进行动平衡。

这是刚性转子动平衡操作的一种常用方法，其目标是使惯性力系的主矢和主矩同时趋近于零。

为此，先在转子上任意选定两个截面I、II（称校正平面）。

在离轴一定距离图11r 、2r （称校正半径），与转子上某一参考标记成夹角1θ、2θ处，分别附加一块质量为1m 、2m 的重块（称校正质量）。

如能使两质量1m 和2m 的惯性力（其大小分别为211ωr m 和222ωr m ，ω为转动角速度）正好与原不平衡转子的惯性力系相平衡，那么就实现了刚性转子的动平衡。

该方法可以不使用专用平衡机，只要求一般的振动测量，适合在转子工作现场进行动平衡作业。

本实验装置中，动平衡机的转子是工作转速低于最低阶临界转速的转子，称为刚性转子，反之称为柔性转子。

转子由调速器设定转速，由涡流传感器测量轴承的水平振动，经前置器、接线盒送给计算机，由专用程序进行处理。

图2转子系统与惯性力系简化两平面影响系数法的过程如下：1．在额定的工作转速或任选的平衡转速下，检测原始不平衡引起的轴承A、B 在水平方向的振动量A A A V V ψ∠=00，B B B V V ψ∠=00，其中0A V 和0B V 是振动位移的幅值，A ψ和B ψ是振动信号对于转子上参考标记有关的参考脉冲的相位角。