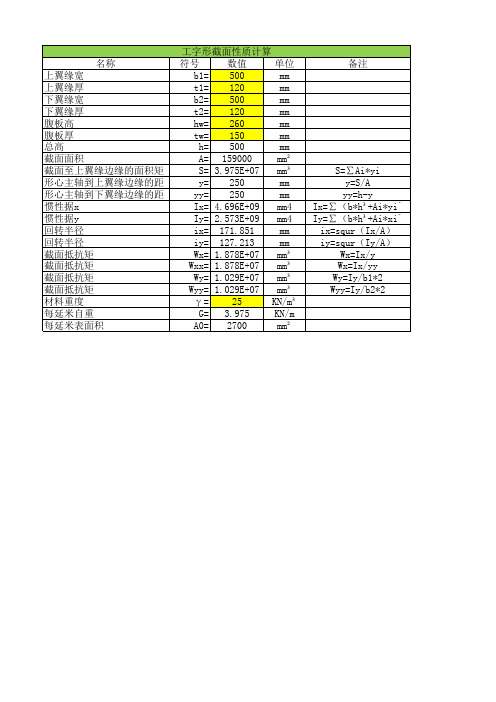
工字型截面性质计算

格式：xls
大小：17.50 KB
文档页数：2

下载文档原格式

/ 2

钢结构基础课后习题答案

4钢结构基础(第二版)课后习题答案(总18页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《钢结构基础》习题参考答案题：答：（1）按制作方法的不同分为型钢截面和组合截面两大类。

型钢截面又可分为热轧型钢和冷弯薄壁型钢两种。

组合截面按连接方法和使用材料的不同，可分为焊接组合截面（焊接截面）、铆接组合截面、钢和混凝土组合截面等。

（2）型钢和组合截面应优先选用型钢截面，它具有加工方便和成本较低的优点。

题：解：由附录1中附表1可得I20a 的截面积为3550mm 2，扣除孔洞后的净面积为3249275.213550A n =⨯⨯-=mm 2。

工字钢较厚板件的厚度为，故由附录4可得Q235钢材的强度设计值为215f =N/mm 2，构件的压应力为2155.138324910450A N 3n <≈⨯==σN/mm 2，即该柱的强度满足要求。

新版教材工字钢为竖放，故应计入工字钢的自重。

工字钢I20a 的重度为m ，故19712.19.8169.27N g =⨯⨯⨯=N ；构件的拉应力为215139.113249197110450A N N 3n g <≈+⨯=+=σN/mm 2，即该柱的强度满足要求。

题：解：1、初选截面假定截面钢板厚度小于16mm ，强度设计值取215f =，125f v =。

可变荷载控制组合：24kN .47251.410.22.1q =⨯+⨯=，永久荷载控制组合：38.27kN 250.71.410.235.1q =⨯⨯+⨯=简支梁的支座反力（未计梁的自重）129.91kN ql/2R ==，跨中的最大弯矩为m 63kN .1785.547.2481ql 81M 22max ⋅≈⨯⨯==，梁所需净截面抵抗矩为 36x max nx 791274mm 2151.051063.178f M W ≈⨯⨯==γ，梁的高度在净空方面无限值条件；依刚度要求，简支梁的容许扰度为l/250，参照表3-2可知其容许最小高度为229mm 24550024l h min ≈==，按经验公式可得梁的经济高度为347mm 3007912747300W 7h 33x e ≈-=-=，由净截面抵抗矩、最小高度和经济高度，按附录1中附表1取工字钢 I36a ，相应的截面抵抗矩3nx 791274mm 875000W >=，截面高度229mm 360h >=且和经济高度接近。

工字形构件的有效截面

工字形构件的有效截面工字形构件是现代工程中常用的一种构件，其形状如同一个“工”字，具有良好的承载能力和加工易度。

工字形构件的有效截面是指在承载过程中起主要作用的截面，也称为抗弯截面或抗剪截面。

在工程设计和使用中，了解并正确计算工字形构件的有效截面至关重要。

本文将介绍工字形构件的有效截面，并探讨其计算方法和应用。

一、工字形构件的剖面结构工字形构件的剖面结构由上盖板、下底板和中央翼缘三部分组成。

上盖板和下底板连接着中央翼缘，构成一个张力或压力载荷下的梁。

工字形构件的中央翼缘一般为等边矩形或等距梯形，翼缘与上盖板和下底板之间的距离称为截面高度h，上盖板和下底板的厚度分别为tf和tw。

由于工字形构件在受载过程中的受力形式较为复杂，因此其有效截面的计算较为繁琐。

二、工字形构件的有效截面分类根据工字形构件在受载过程中的不同受力方式，其有效截面可分为以下几种类型。

1. 抗弯截面工字形构件在纵向受力情况下，上盖板和下底板承担的主要作用是抵抗弯矩。

因此，在纵向受力情况下，工字形构件的有效截面可按照抵抗弯矩能力划分为上盖板、下底板和翼缘三种部分。

一般情况下，上盖板和下底板的有效截面形状为矩形，中央翼缘的有效截面形状则为梯形或直角三角形。

2. 抗剪截面工字形构件在横向受力情况下，中间翼缘承担的主要作用是抵抗剪力。

因此，工字形构件的抗剪截面通常为梯形或等距矩形。

在设计时，应根据结构的要求和受力情况正确地选择有效的抗剪截面，以保证整个结构的稳定性和安全性。

3. 抗扭截面工字形构件在承受扭矩时，其受力状态比较复杂，因此有效截面的计算也受到很大的影响。

计算抗扭截面应综合考虑中央翼缘的宽度、高度、腹板厚度、夹板宽度等多个因素，以确保整个结构的强度和稳定性。

三、工字形构件的有效截面计算方法在实际工程中，计算工字形构件的有效截面时，需要综合考虑其受力情况、材料的强度和稳定性等多种因素。

常用的有效截面计算方法主要包括弯曲底线法、弯矩比法和刚度比法等。

工字形截面性能计算表

工字形截面性质计算名称符号数值单位备注上翼缘宽 b1= 500 mm 上翼缘厚 t1= 120 mm 下翼缘宽 b2= 500 mm 下翼缘厚 t2= 120 mm 腹板高 hw= 260 mm 腹板厚 tw= 150 mm 总高 h= 500 mm 截面面积 A= 159000 mm² 截面至上翼缘边缘的面积矩 S= 3.975E+07 mm³ S=∑Ai*yi 形心主轴到上翼缘边缘的距离 y= 250 mm y=S/A 形心主轴到下翼缘边缘的距离 yy= 250 mm yy=h-y 惯性据x Ix= 4.696E+09 mm4 Ix=∑（b*h³+Ai*yi`²）惯性据y Iy= 2.573E+09 mm4 Iy=∑（b*h³+Ai*xi`²）回转半径 ix= 171.851 mm ix=squr（Ix/A）回转半径 iy= 127.213 mm iy=squr（Iy/A）截面抵抗矩 Wx= 1.878E+07 mm³ Wx=Ix/y 截面抵抗矩 Wxx= 1.878E+07 mm³ Wx=Ix/yy 截面抵抗矩 Wy= 1.029E+07 mm³ Wy=Iy/b1*2 截面抵抗矩 Wyy料重度 γ = 25 KN/m³ 每延米自重 G= 3.975 KN/m 每延米表面积 A0= 2700 mm²

钢结构算量好帮手13：焊接工字截面特性参数计算

注意：以下各公式黑色部分为公式，不可修改，不要填入数值，否
双轴对称焊接工字形截面等截面梁截面特性计算
外包高（H）翼缘宽（b）
300 200
(mm) (mm)
说明：
腹板厚度(tw）
6
(mm)
与相同规格热扎型钢比较，热轧型钢各
翼板厚度（t）
8
(mm) 截面特性比焊接型钢
此公式中惯性矩是根据中国建筑工业出版社第
建筑结构静力计上得来，计算
结果与钢结构教科书中公式（上面）计算结果有一点误差，但误差很小，不影响使用。
IX= Y2=
C27-Y2=
理论单重（G）
38.50 (kg/m) 截面特性偏大，我想可能焊接型钢计算时
截面面积(A)
49.0 (cm2) 忽略了焊缝，不过焊接型钢截面特性设计
惯性矩(Ix)
7966.4 (cm4) 手册上就是这样计算的，热轧型钢截面特
惯性矩(Iy)
1066.7 (cm4) 性敬请查阅相关表格。
惯性半径(ix)
12.75 (cm)
惯性半径(iy)
4.67 (cm)
截面模数(Wx)
531.1 (cm3)
单轴对称焊接工字形截面等截面梁截面特性计算
外包高（H）
300
(mm) 此公式中惯性矩是根据
上翼缘宽（b1）
200
(mm) 中国建筑工业出版社第
下翼缘宽（b2）
200
(mm) 二版《建筑结构静力计
腹板厚度(tw）上翼厚度（t1）下翼厚度（t2）理论单重（G）
6
(mm) 算手册》上得来，计算
8

截面的几何性质面积矩惯性矩惯性积平行移轴公式

HOHAI UNIVERSITY
1
HOHAI UNIVERSITY
2
HOHAI UNIVERSITY
例1 求如图矩形Sz和Sy
解：Sz
ydA
A
ah
ybdy
a
bh(a h) 2
A yC
同样地
Sy
bh(d
b) 2
A
zC
z b/2 b/2 a
y h/2
h/2
dy
y
d
3
HOHAI UNIVERSITY
解： A1 15050mm 2 A2 18050mm 2
150
A3 250 50mm 2
50
C1
yC1 255mm yC2 140mm
5c0
C2
yC3 25mm zC1 zC2 zC3 0
50
C3
z
yC
A1
yC1 A2 yC2 A1 A2 A3
A3
yC 3
250
y
15050 255 18050140 25050 25 mm 15050 18050 25050
i=1
同理
n
Iz =∑ Izi
i=1
n
Iyz =∑ Iyzi
i=1
12
HOHAI UNIVERSITY
例5 图示矩形中，挖去两个直径为d 的圆形，求余下图形对z轴的惯性矩。
b/2 b/2
z
Iz
1 bh3 12
5 d 4
32y13HOHAI UNIVERSITY
14
HOHAI UNIVERSITY
作业题求图示工字形截面对z轴的惯性矩。
b d
z
15

钢结构第四章计算题

y
长细比：
l 3000 x x 43 ix 69.7
3000 y 48 iy 62.5
ly
2、整体稳定性验算
因为绕y轴属于弯扭失稳，必须计算换算长细比yz 因T形截面的剪力中心在翼缘板和腹板中心线的交点，所以剪力中心距形心的距离e0等于yc。即：
2 2 2 2 i0 e0 ix iy 34.252 69.72 62.52
-250×8
回转半径：
Ix 1.1345 108 ix 119.1mm A 8000 x
x y
iy
Iy
3.126 107 62.5mm A 8000
长细比：
x
l x 6000 50.4 ix 119.1
3000 y 48.0 i y 62.5
ly
故整体稳定性满足要求
（2）局部整体稳定验算
b1 250 8 235 8.9 10 0.1 49.56 14.59 t 2 14 235
h0 250 235 31.25 25 0.5 49.56 49.75 tw 8 235
故局部稳定性满足要求
1 Iy 2 1.4 253 25 0.83 3645 cm 4 12

ix
Ix 13250 12.13cm A 90
iy
Iy A

3645 6.36cm 90
2、截面验算
因截面无孔削弱，可不验算强度。
（1）刚度和整体稳定验算
x
l ox 600 49.46 150 ix 12.13
截面面积惯性矩：
A 250 12 2 250 8 8000mm2

钢结构基本原理课后习题与答案完全版

如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版 (1)

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

材料力学考试重点及其公式

外力偶矩传动轴所受的外力偶矩通常不是直接给出，而是根据轴的转速 n 与传递的功率P 来计算当功率P 单位为千瓦（kW ,转速为n （r/min ）时，外力偶矩为PM e =9549 （N.m ）n当功率P 单位为马力（PS ，转速为n （r/min ）时，外力偶矩为PM e =7024（N.m ） n2.5.2切应力计算公式T P横截面上某一点切应力大小为p =—（3-12）1 p式中I p 为该截面对圆心的极惯性矩，「为欲求的点至圆心的距离。

式中W t =5称为扭转截面系数，R 为圆截面半径。

R2.5.3切应力公式讨论（1）切应力公式（3-12）和式（3-13）适用于材料在线弹性范围内、小变形时的等圆截面直杆；对小锥度圆截面直杆以及阶梯形圆轴亦可近似应用，其误差在工程允许范围内。

（2）极惯性矩I p 和扭转截面系数W t 是截面几何特征量，计算公式见表3-3。

在面积不变情况下，材料离散程度高，其值愈大；反映出轴抵抗扭转破坏和变形的能力愈强。

因此，设计空心轴比实心轴更为合理。

表实心圆（外径为d ）.4 ndI p一 p32nd 3 W t =—— 16空心圆（外径为D, 内径为d ）HD 44I p - ”(I a 4) 32d a - D兀D 4 4 w =」H1—a 4)162.5.4强度条件圆轴扭转时，全轴中最大切应力不得超过材料允许极限值，否则将发生破坏。

因此，强度条件为材料的许用切应力圆截面周边上的切应力为maxTW t(3-13)max/ 、匚^t .max(3-14)对等圆截面直杆T maxmaxW t（3-15）式中L 丨为3.1.1中性层的曲率与弯矩的关系1 _JM 匚=EI(3-16)式中，r 是变形后梁轴线的曲率半径；E 是材料的弹性模量；I E 是横截面对中性轴Z 轴的惯性矩。

3.1.2横截面上各点弯曲正应力计算公式-挣(3-17)式中，M 是横截面上的弯矩；I z 的意义同上；y 是欲求正应力的点到中性轴的距离I 1 jr式中，W z=h 称为抗弯截面系数。

7-2对称配筋、工形截面偏心受压、双向偏心受压构件计算

⑤当ηei(或M／N＋ea)＞0.3h，且Nb＞N时，为大偏心受压。x=N/α1fcb
(7-29)或式(7-30)求出As=As’。
淮海工学院土木工程系（/jiangong/index.htm）
第7章钢筋混凝土偏心受力构件承载力计算
Huaihai Institute of Technology
第7章钢筋混凝土偏心受力构件承载力计算
Huaihai Institute of Technology
②小偏心受压情况(ξ＞ξb)
在这种情况下。通常受压区高度已进人腹板(x＞hf ’)，按下列公式计算
N 1 f c Ac f y A s s A s
' '
(7-38)
Ne 1 f c S c f y A s h0 a s
淮海工学院土木工程系（/jiangong/index.htm）
第7章钢筋混凝土偏心受力构件承载力计算
Huaihai Institute of Technology
⑴非对称配筋截面
①大偏心受压情况(ξ≤ξb)
与T形截面受弯构件相同，按受压区高度x的不同可分为两类(图7-17)。

'
Ne 1 f c bx h0 0 . 5 x b f b h f h0 0 . 5 h f
' '

(7-37)
h 2
f y A s h0 a s
' ' '

’ 公式适用条件： x≥2as x≤ξbh0
e ei
as
淮海工学院土木工程系（/jiangong/index.htm）

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

工字型截面性质计算
b＝ t＝ bb＝ tt＝ hw＝ tw＝ h＝ A＝ S＝ y＝ yy＝ Ix＝ Iy＝ ix＝ iy＝ Wx＝ Wxy＝ Wy＝ Wyy＝ γ = G＝ 200 16 350 16 1100 10 1132 19800 1.2840E+07 6.4851E+02 4.8349E+02 3.7632E+09 6.7925E+07 4.3596E+02 543;06 7.7832E+06 6.7925E+05 3.8814E+05 78.5 1.5543 (mm) (mm) (mm) (mm) (mm) (mm) (mm) (mm) (mm3) (mm) (mm) (mm4) (mm4) (mm) (mm) (mm3) (mm3) (mm3) (mm3) (kN/m3) (kN/m)
截面性质计算
上翼缘宽 b 上翼缘厚 t 下翼缘宽 bb 下翼缘厚 tt 腹板净高 h0 腹板厚 tw 总高 h 截面面积 A 截面对上翼缘边缘轴的面积矩 S=∑Ai*yi 形心主轴到上翼缘边缘的距离 y=S/A 形心主轴到下翼缘边缘的距离 yy=h-y 转动惯量 Ix=∑(Ix1+Ai*yi^2) 转动惯量 Iy=∑(Iy1+Ai*xi^2) 回转半径 ix=sqrt(Ix/A) 回转半径 iy=sqrt(Iy/A) 截面抵抗矩 Wx=Ix/b*2 截面抵抗矩 Wx=Ix/bb*2 截面抵抗矩 Wy=Iy/t*2 截面抵抗矩 Wy=Iy/tt*2 材料重度 γ (钢材为78.5kN/m3) 每延米自重 G=Aγ