5.2 惯性矩和平行移轴公式

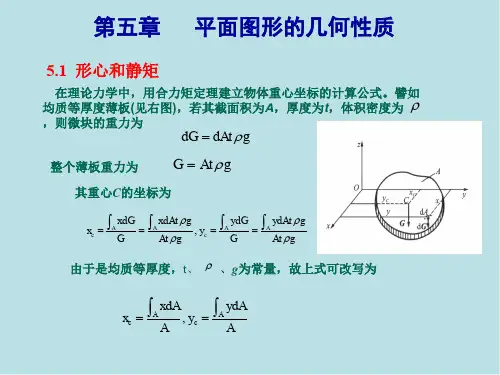
惯性矩的计算⽅法第1节静矩和形⼼静矩和形⼼任何受⼒构件的承载能⼒不仅与材料性能和加载⽅式有关，⽽且与构件截⾯的⼏何形状和尺⼨有关．如：计算杆的拉伸与压缩变形时⽤到截⾯⾯积 A ，计算圆轴扭转变形时⽤到横截⾯的极惯性矩 I等． A 、 I等是从不同⾓度反映了截⾯的⼏何特性，因此称它们为截⾯图形的⼏何性质．静矩和形⼼设有⼀任意截⾯图形如图 4 — 1 所⽰，其⾯积为 A ．选取直⾓坐标系 yoz ，在坐标为 (y,z) 处取⼀微⼩⾯积 dA ，定义微⾯积dA 乘以到 y 轴的距离 z ，沿整个截⾯的积分，为图形对 y 轴的静矩 S，其数学表达式(4 -1a )同理，图形对 z 轴的静矩为(4-1b)图 4-1截⾯静矩与坐标轴的选取有关，它随坐标轴 y 、 z 的不同⽽不同．所以静矩的数值可能是正，也可能是负或是零．静矩的量纲为长度的三次⽅．确定截⾯图形的形⼼位置 ( 图 4-1 中 C 点 ):(4 -2a )(4-2b)式中 y、 z 为截⾯图形形⼼的坐标值．若把式 (4-2) 改写成(4-3)性质：若截⾯图形的静矩等于零，则此坐标轴必定通过截⾯的形⼼．若坐标轴通过截⾯形⼼，则截⾯对此轴的静矩必为零．由于截⾯图形的对称轴必定通过截⾯形⼼，故图形对其对称轴的静矩恒为零。

4 ）⼯程实际中，有些构件的截⾯形状⽐较复杂，将这些复杂的截⾯形状看成是由若⼲简单图形 ( 如矩形、圆形等 ) 组合⽽成的．对于这样的组合截⾯图形，计算静矩 (S) 与形⼼坐标 (y、 z ) 时，可⽤以下公式(4-4)(4-5)式中 A， y ， z 分别表⽰第个简单图形的⾯积及其形⼼坐标值， n 为组成组合图形的简单图形个数．即：组合图形对某⼀轴的静矩等于组成它的简单图形对同⼀轴的静矩的代数和．组合图形的形⼼坐标值等于组合图形对相应坐标轴的静矩除以组合图形的⾯积．组合截⾯图形有时还可以认为是由⼀种简单图形减去另⼀种简单图形所组成的．例 4-1 已知 T 形截⾯尺⼨如图 4-2 所⽰，试确定此截⾯的形⼼坐标值．图 4-2解： (1) 选参考轴为 y 轴， z 轴为对称轴，(2) 将图形分成 I 、两个矩形，则(3) 代⼊公式 (4-5)惯性矩、惯性积和惯性半径设任⼀截⾯图形 ( 图 4 — 3) ，其⾯积为 A ．选取直⾓坐标系 yoz ，在坐标为 (y 、 z) 处取⼀微⼩⾯积 dA ，定义此微⾯积 dA 乘以到坐标原点o的距离的平⽅，沿整个截⾯积分，为截⾯图形的极惯性矩 I．微⾯积 dA 乘以到坐标轴 y 的距离的平⽅，沿整个截⾯积分为截⾯图形对 y 轴的惯性矩 I．极惯性矩、惯性矩常简称极惯矩、惯矩．数学表达式为极惯性矩 (4-6)对 y 轴惯性矩 (4 -7a )同理，对 z 轴惯性矩 (4-7b)图 4-3由图 4-3 看到所以有即(4-8) 式 (4 — 8) 说明截⾯对任⼀对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。

前引360知识：惯性矩是一个物理量，通常被用作描述一个物体抵抗弯曲的能力。

惯性矩的国际单位为(m^4)。

百度知识：惯性矩(moment of inertia of an area)是一个几何量，通常被用作描述截面抵抗弯曲的性质。

惯性矩的国际单位为(m4)。

即面积二次矩，也称面积惯性矩，而这个概念与质量惯性矩（即转动惯量）是不同概念。

截面惯性矩（I=截面面积X截面轴向长度的二次方）结构构件惯性矩I x结构设计和计算过程中，构件惯性矩I x为截面各微元面积与各微元至与X轴线平行或重合的中和轴距离二次方乘积的积分。

主要用来计算弯矩作用下绕X轴的截面抗弯刚度。

结构构件惯性矩I y结构设计和计算过程中，构件惯性矩I y为截面各微元面积与各微元至与Y轴线平行或重合的中和轴距离二次方乘积的积分。

主要用来计算弯矩作用下绕Y轴的截面抗弯刚度。

工程构件典型截面几何性质的计算2.1面积矩1．面积矩的定义图2-2.1任意截面的几何图形如图2-2.1所示为一任意截面的几何图形(以下简称图形)。

定义：积分和分别定义为该图形对z轴和y轴的面积矩或静矩，用符号S z和S y，来表示，如式(2—2.1)(2—2.1)面积矩的数值可正、可负，也可为零。

面积矩的量纲是长度的三次方，其常用单位为m3或mm3。

2．面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成，如式(2—2.3)(2—2.3)面积矩的几何意义：图形的形心相对于指定的坐标轴之间距离的远近程度。

图形形心相对于某一坐标距离愈远，对该轴的静距（面积矩）绝对值愈大。

图形对通过其形心的轴的静距（面积矩）等于零；反之，图形对某一轴的面积矩等于零，该轴一定通过图形形心。

形心确定的规律：（a）图形有对称轴时，形心必在此对称轴上。

（b）图形有两个对称轴时，形心必在此两对称轴的交点处。

3．组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。

本章重点1、静矩与形心2、惯性矩、极惯性矩和惯性积3、平行移轴公式、转轴公式关键概念静矩、惯性矩、极惯性矩、惯性积、主惯性轴、形心主惯性轴目录§I-1 静矩和形心§I-2极惯性矩·惯性矩·惯性积§I-3 平行移轴公式§I-4 惯性矩和惯性积的转轴公式.截面的§I -1 静矩和形心一、基本概念1. 静矩（或一次矩）O xd A y yx C x ydA x ⋅——微面积对y 轴的静矩dA y ⋅——微面积对x 轴的静矩A x S A y d ⎰=A y S A x d ⎰=——整个平面图形对y 轴的静矩——整个平面图形对x 轴的静矩2.形心坐标公式AS A Ay y A S A A x x x A yA ====⎰⎰d d 常用单位：m 3或mm 3。

数值：可为正、负或0 。

3.静矩与形心坐标的关系yA S x A S x y ==推论：截面对形心轴的静矩恒为0，反之，亦然。

1.组合截面的静矩根据静矩的定义：整个平面图形对某轴的静矩应等于它的各组成部分对同一轴的静矩的代数和，即：∑=∑===ni i i x n i i i y y A S x A S 11 和面积。

个简单图形的形心坐标分别为第和　式中：　i A y x i i i ,二、讨论：2.组合截面的形心坐标公式∑=∑===n i i i x n i i i y y A S x A S 11 组合截面静矩∑==n i i A A 1组合截面面积组合截面的形心坐标公式为：∑∑==∑∑======n i i ni i i x n i i n i i i y A y A A S y A x A A S x 1111 ，例I —1：计算由抛物线、y 轴和z 轴所围成的平面图形对y 轴和z 轴的静矩，并确定图形的形心坐标。

z h y b =-⎛⎝ ⎫⎭⎪122O y z 解：S z A y A =⎰2d S y A z A =⎰d =-⎛⎝ ⎫⎭⎪⎰12102222b h y b y d =-⎛⎝ ⎫⎭⎪⎰yh y b y b0221d =4152bh =b h 24O y z y d y bh A A A =⎰d =-⎛⎝ ⎫⎭⎪⎰0221b h y b y d =23bh 形心坐标为:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧======52321548332422hbh bh A S z bbh bhA S y y C z C例I —2：确定图示图形形心C 的位置。

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点：(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形，取其单元如面积dA ，定义它对任意轴的一次矩为它对该轴的静矩，即ydAdSx xdA dS y == 整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS （I-1） 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0AS y x= ， A S x y = （I-2）推论1 如果y 轴通过形心（即0=x ），则静矩0=y S ；同理，如果x 轴通过形心（即0=y ），则静矩0=Sx ；反之也成立。

推论2 如果x 、y 轴均为图形的对称轴，则其交点即为图形形心；如果y 轴为图形对称轴，则图形形心必在此轴上。

3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成，且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ；；，则图形对y 轴和x轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii ni yi y y A S S x A S 1111S （I-3）截面图形的形心坐标为∑∑===ni ini ii AxA x 11 ， ∑∑===ni ini ii AyA y 11 （I-4）4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。

(2) 静矩有的单位为3m 。

(3) 静矩的数值可正可负，也可为零。

图形对任意形心轴的静矩必定为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。

(4) 若已知图形的形心坐标。

则可由式（I-1）求图形对坐标轴的静矩。

若已知图形对坐标轴的静矩，则可由式（I-2）求图形的形心坐标。

组合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静矩，然后由式（I-4）求出其形心坐标。

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点：(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形，取其单元如面积dA ，定义它对任意轴的一次矩为它对该轴的静矩，即ydAdSx xdA dS y == 整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS （I-1） 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0AS y x=， A S x y = （I-2）推论1 如果y 轴通过形心（即0=x ），则静矩0=y S ；同理，如果x 轴通过形心（即0=y ），则静矩0=Sx ；反之也成立。

推论2 如果x 、y 轴均为图形的对称轴，则其交点即为图形形心；如果y 轴为图形对称轴，则图形形心必在此轴上。

3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成，且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ；；，则图形对y 轴和x 轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii n i yi y y A S S x A S 1111S （I-3）截面图形的形心坐标为∑∑===ni ini ii AxA x 11 ， ∑∑===ni ini ii AyA y 11 （I-4）4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的，故静矩与坐标轴有关。

(2) 静矩有的单位为3m 。

(3) 静矩的数值可正可负，也可为零。

图形对任意形心轴的静矩必定为零，反之，若图形对某一轴的静矩为零，则该轴必通过图形的形心。

(4) 若已知图形的形心坐标。

则可由式（I-1）求图形对坐标轴的静矩。

若已知图形对坐标轴的静矩，则可由式（I-2）求图形的形心坐标。

组合图形的形心位置，通常是先由式（I-3）求出图形对某一坐标系的静矩，然后由式（I-4）求出其形心坐标。

I等． I等是从不同角度反映了截S，其数学表达式(4 -1a )(4-1b)(4 -2a )(4-2b)式中 y、 z 为截面图形形心的坐标值．若把式 (4-2) 改写成(4-3)性质：•若截面图形的静矩等于零，则此坐标轴必定通过截面的形心．•若坐标轴通过截面形心，则截面对此轴的静矩必为零．•由于截面图形的对称轴必定通过截面形心，故图形对其对称轴的静矩恒为零。

4 ）工程实际中，有些构件的截面形状比较复杂，将这些复杂的截面形状看成是由若干简单图形 ( 如矩形、圆形等 ) 组合而成的．对于这样的组合截面图形，计算静矩 (S) 与形心坐标 (y、 z ) 时，可用以下公式(4-4)(4-5)式中 A， y ， z 分别表示第个简单图形的面积及其形心坐标值， n 为组成组合图形的简单图形个数．即：组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和．组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积．组合截面图形有时还可以认为是由一种简单图形减去另一种简单图形所组成的．例 4-1 已知 T 形截面尺寸如图 4-2 所示，试确定此截面的形心坐标值．、两个矩形，则设任一截面图形 ( 图 4 — 3) ，其面积为 A ．选取直角坐标系 yoz ，在坐标为 (y 、 z) 处取一微小面积 dA ，定义此微面积 dA 乘以到坐标原点o的距离的平方，沿整个截面积分，为截面图形的极惯性矩 I．微面积 dA 乘以到坐标轴 y 的距离的平方，沿整个截面积分为截面图形对 y 轴的惯性矩 I．极惯性矩、惯性矩常简称极惯矩、惯矩．数学表达式为极惯性矩 (4-6)对 y 轴惯性矩 (4 -7a )同理，对 z 轴惯性矩 (4-7b)由图 4-3 看到所以有即(4-8) 式 (4 — 8) 说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。

在任一截面图形中 ( 图 4 —3) ，取微面积 dA 与它的坐标 z 、 y 值的乘积，沿整个截面积分，定义此积分为截面图形对 y 、z 轴的惯性积，简称惯积．表达式为(4-9)惯性矩、极惯性矩与惯性积的量纲均为长度的四次方． I,I,I恒为正值．而惯性积 I其值能为正，可能为负，也可能为零．若选取的坐标系中，有一轴是截面的对称轴，则截面图形对此轴的惯性积必等于零．当截面图形对某一对正交坐标轴的惯性积等于零时，称此对坐标轴为截面图形的主惯性轴．对主惯性轴的惯性矩称为主惯性矩．而通过图形形心的主惯性轴称为形心主惯性轴 ( 或称主形心惯轴 ) ．截面对形心主惯性轴的惯性矩称为形心主惯性矩 ( 或称主形心惯矩 ) ．例如，图 4-4 中若这对 yz 轴通过截面形心，则它们就是形心主惯性轴．对这两个轴的惯性矩即为形心主惯性矩．工程应用中 ( 如压杆稳定中 ) ，有时将惯性矩表示成截面面积与某一长度平方的乘积，即,或写成, （ 4-10 ）式中 i分别称为截面图形对 y 轴、 z 轴的惯性半径．其量纲为长度的一次方．例 4-2 已知矩形截面的尺寸 b,h( 图 4-5) ，试求它的形心主惯性矩．解：取形心主惯性轴 ( 即对称轴 )y,z ，及 dA=dy，代入公式 (I— 7a ,) 得同理：例 4-3 设圆的直径为 D( 图 4-6) ，试求图形对其形心轴的惯性矩及惯性半径值．解： (1) 求惯性矩因为图形对称， y,z 为对称轴，所以 I＝ I这是较简单的解法．本例也可取出图 4-6 上的微面积 dA ，按积分法来求得。