2021版高考数学一轮复习单元评估检测(四)苏教版

江苏省扬州市2021届新高考数学四模考试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若x yi +(,)x y ∈R 与31i i +-互为共轭复数，则x y +=（ ） A ．0B ．3C ．－1D ．4 【答案】C【解析】【分析】 计算3121i i i+=+-，由共轭复数的概念解得,x y 即可. 【详解】3121i i i+=+-Q ，又由共轭复数概念得：x 1,y 2==-， 1x y ∴+=-.故选：C【点睛】本题主要考查了复数的运算，共轭复数的概念.2．设x 、y 、z 是空间中不同的直线或平面，对下列四种情形：①x 、y 、z 均为直线；②x 、y 是直线，z 是平面；③z 是直线，x 、y 是平面；④x 、y 、z 均为平面.其中使“x z ⊥且y z x y ⊥⇒∥”为真命题的是（ ） A ．③④B ．①③C ．②③D ．①②【答案】C【解析】【分析】①举反例，如直线x 、y 、z 位于正方体的三条共点棱时②用垂直于同一平面的两直线平行判断.③用垂直于同一直线的两平面平行判断.④举例，如x 、y 、z 位于正方体的三个共点侧面时.【详解】①当直线x 、y 、z 位于正方体的三条共点棱时,不正确；②因为垂直于同一平面的两直线平行,正确；③因为垂直于同一直线的两平面平行,正确；④如x 、y 、z 位于正方体的三个共点侧面时, 不正确.故选:C.【点睛】此题考查立体几何中线面关系，选择题一般可通过特殊值法进行排除，属于简单题目.3．《九章算术》“少广”算法中有这样一个数的序列：列出“全步”（整数部分）及诸分子分母，以最下面的分母遍乘各分子和“全步”，各自以分母去约其分子，将所得能通分之分数进行通分约简，又用最下面的分母去遍乘诸（未通者）分子和以通之数，逐个照此同样方法，直至全部为整数，例如：2n =及3n =时，如图：记n S 为每个序列中最后一列数之和，则6S 为（ ）A ．147B ．294C ．882D ．1764【答案】A【解析】【分析】根据题目所给的步骤进行计算，由此求得6S 的值.【详解】依题意列表如下： 上列乘6 上列乘5 上列乘21 6 30 6012 3 15 3013 2 10 2014 32 152 1515 65 6 1216 1 5 10所以6603020151210147S =+++++=.故选：A【点睛】本小题主要考查合情推理，考查中国古代数学文化，属于基础题.4．设0.08log 0.04a =，0.3log 0.2b =，0.040.3c =，则a 、b 、c 的大小关系为（ ）A ．c b a >>B ．a b c >>C ．b c a >>D ．b a c >> 【答案】D【解析】【分析】【详解】 因为0.080.080.080.08log 0.042log 0.2log 0.2log 10a ===>=，0.30.3log 0.2log 10b =>=， 所以0.20.211log 0.08,log 0.3a b==且0.2log y x =在()0,∞+上单调递减，且0.080.3< 所以11a b>，所以b a >， 又因为0.080.08log0.2log 0.081a =>=，0.0400.30.31c =<=，所以a c >，所以b a c >>.故选：D.【点睛】本题考查利用指对数函数的单调性比较指对数的大小，难度一般.除了可以直接利用单调性比较大小，还可以根据中间值“0,1”比较大小.5．为比较甲、乙两名高中学生的数学素养，对课程标准中规定的数学六大素养进行指标测验（指标值满分为100分，分值高者为优），根据测验情况绘制了如图所示的六大素养指标雷达图，则下面叙述不正确的是（ ）A ．甲的数据分析素养优于乙B ．乙的数据分析素养优于数学建模素养C ．甲的六大素养整体水平优于乙D ．甲的六大素养中数学运算最强【答案】D【解析】根据所给的雷达图逐个选项分析即可.【详解】对于A ，甲的数据分析素养为100分，乙的数据分析素养为80分，故甲的数据分析素养优于乙，故A 正确；对于B ，乙的数据分析素养为80分，数学建模素养为60分，故乙的数据分析素养优于数学建模素养，故B 正确；对于C ，甲的六大素养整体水平平均得分为10080100801008031063+++++=， 乙的六大素养整体水平均得分为806080606010025063+++++=，故C 正确； 对于D ，甲的六大素养中数学运算为80分，不是最强的，故D 错误；故选：D【点睛】本题考查了样本数据的特征、平均数的计算，考查了学生的数据处理能力，属于基础题.6．已知集合A ＝{0，1}，B ＝{0，1，2}，则满足A ∪C ＝B 的集合C 的个数为（ ）A ．4B ．3C ．2D ．1【答案】A【解析】【分析】由A C B ⋃=可确定集合C 中元素一定有的元素，然后列出满足题意的情况，得到答案.【详解】由A C B ⋃=可知集合C 中一定有元素2，所以符合要求的集合C 有{}{}{}{}2,2,0,2,1,2,0,1，共4种情况，所以选A 项.【点睛】考查集合并集运算，属于简单题.7．已知双曲线C ：2222x y a b-=1（a ＞0，b ＞0）的焦距为8，一条渐近线方程为y =，则C 为（ ） A ．221412x y -= B ．221124x y -= C ．2211648x y -= D ．2214816x y -= 【答案】A【分析】由题意求得c 与b a 的值，结合隐含条件列式求得a 2，b 2，则答案可求. 【详解】由题意，2c ＝8，则c ＝4，又b a=a 2+b 2＝c 2， 解得a 2＝4，b 2＝12.∴双曲线C 的方程为221412x y -=. 故选：A.【点睛】本题考查双曲线的简单性质，属于基础题.8．根据散点图，对两个具有非线性关系的相关变量x ，y 进行回归分析，设u= lny ，v=(x-4)2，利用最小二乘法，得到线性回归方程为ˆu=-0.5v+2，则变量y 的最大值的估计值是（ ） A ．eB ．e 2C ．ln2D ．2ln2【答案】B【解析】【分析】 将u= lny ，v=(x-4)2代入线性回归方程ˆu=-0.5v+2，利用指数函数和二次函数的性质可得最大估计值. 【详解】解：将u= lny ，v=(x -4)2代入线性回归方程ˆu=-0.5v+2得： ()2ln 0.542y x =--+，即()20.542x y e--+=， 当4x =时，()20.542x --+取到最大值2，因为x y e =在R 上单调递增，则()20.542x y e --+=取到最大值2e .故选：B.【点睛】本题考查了非线性相关的二次拟合问题，考查复合型指数函数的最值，是基础题,.9．已知函数21,0()ln ,0x x f x x x +≤⎧=⎨>⎩,则方程[]()3f f x =的实数根的个数是（ ） A ．6B ．3C ．4D ．5【答案】D【解析】画出函数21,0()ln ,0x x f x x x +≤⎧=⎨>⎩,将方程[]()3f f x =看作()(),3t f x f t ==交点个数，运用图象判断根的个数．【详解】画出函数21,0()ln ,0x x f x x x +≤⎧=⎨>⎩令()(),3t f x f t =∴=有两解()()120,1,1,+t t ∈∈∞ ，则()()12,t f x f x t ==分别有3个，2个解，故方程[]()3f f x =的实数根的个数是3+2=5个故选：D【点睛】本题综合考查了函数的图象的运用，分类思想的运用，数学结合的思想判断方程的根，难度较大，属于中档题．10．某市政府决定派遣8名干部（5男3女）分成两个小组，到该市甲、乙两个县去检查扶贫工作，若要求每组至少3人，且女干部不能单独成组，则不同的派遣方案共有（ ）种A ．240B ．320C ．180D ．120【答案】C【解析】【分析】在所有两组至少都是3人的分组中减去3名女干部单独成一组的情况，再将这两组分配，利用分步乘法计数原理可得出结果.【详解】两组至少都是3人，则分组中两组的人数分别为3、5或4、4，又因为3名女干部不能单独成一组，则不同的派遣方案种数为432882221180C C A A ⎛⎫+-= ⎪⎝⎭. 故选：C.【点睛】本题考查排列组合的综合问题，涉及分组分配问题，考查计算能力，属于中等题.11．设n S 为等差数列{}n a 的前n 项和，若33a =-，77S =-，则n S 的最小值为（ ）A ．12-B ．15-C ．16-D ．18-【答案】C【解析】【分析】根据已知条件求得等差数列{}n a 的通项公式，判断出n S 最小时n 的值，由此求得n S 的最小值.【详解】 依题意11237217a d a d +=-⎧⎨+=-⎩，解得17,2a d =-=，所以29n a n =-.由290n a n =-≤解得92n ≤，所以前n 项和中，前4项的和最小，且4146281216S a d =+=-+=-.故选：C【点睛】本小题主要考查等差数列通项公式和前n 项和公式的基本量计算，考查等差数列前n 项和最值的求法，属于基础题.12．公比为2的等比数列{}n a 中存在两项m a ，n a ，满足2132m n a a a =，则14m n +的最小值为（ ） A ．97 B ．53 C ．43 D ．1310【答案】D【解析】【分析】根据已知条件和等比数列的通项公式，求出,m n 关系，即可求解.【详解】22211232,7m n m n a a a a m n +-==∴+=，当1,6m n ==时，1453m n +=，当2,5m n ==时，141310m n +=， 当3,4m n ==时，1443m n +=，当4,3m n ==时，141912m n +=，当5,2m n ==时，14115m n +=，当6,1m n ==时，14256m n +=， 14m n +最小值为1310. 故选:D.【点睛】本题考查等比数列通项公式，注意,m n 为正整数，如用基本不等式要注意能否取到等号，属于基础题.二、填空题：本题共4小题，每小题5分，共20分。

第40课等比数列【自主学习】第40课等比数列(本课时对应同学用书第页)自主学习回归教材1.(必修5P49习题1改编)已知数列{a n}为正项等比数列，a2=9，a4=4，则数列{a n}的通项公式a n=.【答案】9·-2 23n⎛⎫ ⎪⎝⎭【解析】设等比数列{a n}的公比为q，则q2=42aa=49.又由于q>0，所以q=23，所以an=9·-223n⎛⎫⎪⎝⎭.2.(必修5P49习题1改编)假如-1，a，b，c，-9成等比数列，那么b=，a·c=.【答案】-39【解析】由等比数列的性质可得ac=(-1)×(-9)=9；b×b=9，且b与奇数项的符号相同，故b=-3.3.(必修5P58练习6改编)若对于实数x，有a n=x n，则数列{a n}的前n项和S n=.【答案】001(1-)011-nxn xx xx xx⎧⎪=⎪⎪=⎨⎪⎪≠≠⎪⎩，，，，，且【解析】当x=0时，S n=0；当x=1时，S n=n；当x≠0且x≠1时，S n=(1-)1-nx xx.4.(必修5P61习题3改编)若等比数列的通项公式为a n=4×31-n，则数列{a n}是数列.(填“递增”或“递减”)【答案】递减5.(必修5P67习题3改编)设{a n}是等比数列，给出下列四个命题：①{2na}是等比数列；②{na an+1}是等比数列；③1na⎧⎫⎨⎬⎩⎭是等比数列；④{lg|an|}是等比数列.其中正确的命题是.(填序号)【答案】①②③【解析】④是等差数列.1.等比数列的定义及通项假如一个数列从其次项起，每一项与它的前一项的比都等于同一个常数，那么这个数列就叫作等比数列.这个常数叫作等比数列的公比.等比数列的通项公式：a n=a1q n-1=1aq·q n(n∈N*)；推广：a n=a m q n-m.2.等比数列求和公式S n=11(1-)11-1na qqqna q⎧≠⎪⎨⎪=⎩，，，=11-11-1na a qqqna q⎧≠⎪⎨⎪=⎩，，，.3.等比数列的性质设数列{a n}是等比数列，公比为q.(1)若m+n=p+q(m，n，p，q∈N*)，则a m a n=a p a q ；(2)数列{ka n}(k为非零常数)，1na⎧⎫⎨⎬⎩⎭，{k n a}(k∈Z且为常数)也是等比数列；(3)每隔k项取出一项(k∈N*)，按原来的挨次排列，所得新数列仍为等比数列；(4)若{a n}的前n项和为S n，则S k，S2k-S k，S3k-S2k，…仍组成等比数列(各项不为0).【要点导学】要点导学各个击破等比数列的基本量运算例1(2021·苏锡常镇、宿迁一调)已知等比数列{a n}的各项均为正数，若a4=22a，a2+a4=516，求数列{a n}的通项公式.【思维引导】将a4=a2q2代入a4=22a，a2+a4=516，求出q及a2，再求a n.【解答】设等比数列{a n}的公比为q.由于a4=22 a，所以a2q2=22a.又a2≠0，所以a2=q2.由于22a+a2-516=0，所以a2=14或a2=-54(舍去)，所以q2=14.又q>0，所以q=12，所以an=a2q n-2=q n=12n⎛⎫⎪⎝⎭.【精要点评】此题主要考查等比数列的通项公式.求等比数列的通项就是要求基本量a1和q，要留意q=1的状况.【高频考点·题组强化】1.(2021·广东卷)若三个正数a，b，c成等比数列，其中a6c6，则b=.【答案】1【解析】由于三个正数a，b，c成等比数列，所以b2=ac66又由于b>0，所以b=1.2.(2022·苏州期中)已知等比数列{a n}的公比大于1，若a5-a1=15，a4-a2=6，则a3=.【答案】4【解析】设等比数列{a n}的公比为q，由题意知411311-15-6a q aa q a q⎧=⎨=⎩，，解得112aq=⎧⎨=⎩，或1-1612aq=⎧⎪⎨=⎪⎩，(舍去)，故a3=a1q2=1×22=4.3.(2022·扬州一模)设S n是等比数列{a n}的前n项的和，若a5+2a10=0，则2010SS=.【答案】54【解析】设等比数列公比为q，则由a5+2a10=0，得q5=-12，所以2010SS=201101(1-)1-(1-)1-a qqa qq=1+q10=1+14=54.4.已知等比数列{a n}的各项均为正数，且a1，12a3，2a2成等差数列，那么91078a aa a++=.【答案】3+22【解析】依题意可得2×3 1 2 a⎛⎫⎪⎝⎭=a1+2a2，即a3=a1+2a2，则有a1q2=a1+2a1q，可得q2=1+2q，解得q=1+2或q=1-2(舍去)，所以91078a aa a++=89116711a q a qa q a q++=231q qq++=q2=3+22.5.(2021·全国卷)在数列{a n}中，已知a1=2，a n+1=2a n，S n为{a n}的前n项和.若S n=126，则n=.【答案】6【解析】由a1=2，a n+1=2a n可知数列{a n}为等比数列，公比为2，所以S n=2(1-2)1-2n=126，得n=6.等比数列的通项公式例2设数列{a n}的前n项和为S n，a1=1，S n+1=4a n+2(n∈N*)，若b n=a n+1-2a n，求数列{b n}的通项公式.【思维引导】由S n+2=4a n+1+2，a n+2=S n+2-S n+1=4(a n+1-a n)，得a n+2-2a n+1=2(a n+1-2a n)，所以b n+1=2b n，再求出首项b1=3≠0，判定{b n}是公比为2的等比数列.【解答】由于a1=1，S n+1=4a n+2(n∈N*)，所以S n+2=4a n+1+2.则a n+2=S n+2-S n+1=4(a n+1-a n)，所以a n+2-2a n+1=2(a n+1-2a n)，即b n+1=2b n，所以{b n}是公比为2的等比数列，且b1=a2-2a1.由于a1=1，a2+a1=S2，即a2+a1=4a1+2，所以a2=3a1+2=5，所以b1=5-2=3.所以b n=3·2n-1.【精要点评】推断一个数列是不是等比数列，依据定义，看前一项与后一项的比是不是同一个常数，同时还要求b1≠0.等比数列的求和问题例3已知公比不为1的等比数列{a n}的首项a1=12，前n项和为Sn，且a4+S4，a5+S5，a6+S6成等差数列.(1)求等比数列{a n}的通项公式及前n项和S n；(2)对n∈N*，在a n与a n+1之间插入3n个数，使这3n+2个数成等差数列，记插入的这3n个数的和为b n，求数列{b n}的前n项和T n.【思维引导】(1)由等比数列的通项公式可求得数列{a n}的通项公式.(2)由等差数列的前n项和公式可得插入的3n个数的和为b n=12n na a++·3n，由(1)可求得b n的表达式，再依据等比数列的前n 项和公式即可得到结论.【解答】(1)设等比数列{a n}的公比为q，由于a4+S4，a5+S5，a6+S6成等差数列，所以a5+S5-a4-S4=a6+S6-a5-S5，即2a6-3a5+a4=0，所以2q2-3q+1=0，由于q≠1，所以q=12，所以等比数列{an}的通项公式为a n=12n.S n=111-2211-2n⎡⎤⎛⎫⎢⎥⎪⎝⎭⎢⎥⎣⎦=1-12n⎛⎫⎪⎝⎭.(2)b n=12n na a++·3n=3342n⎛⎫⎪⎝⎭，所以T n=133-322341-2n+⎛⎫⎪⎝⎭=93-142n⎡⎤⎛⎫⎢⎥⎪⎝⎭⎢⎥⎣⎦.【精要点评】本题主要考查等比数列前n项和公式的运用，同时考查构造新数列求通项、求和的方法.变式(2021·四川卷)设数列{a n}的前n项和S n满足S n=2a n-a3，且a1，a2+1，a3成等差数列.(1)求数列{a n}的通项公式；(2)求数列1na⎧⎫⎨⎬⎩⎭的前n项和Tn.【解答】(1)由于S n=2a n-a3，所以a n=S n-S n-1=2a n-2a n-1(n≥2)，即a n=2a n-1(n≥2).从而a2=2a1，a3=2a2=4a1，又由于a1，a2+1，a3成等差数列，即a1+a3=2(a2+1)，所以a1+4a1=2(2a1+1)，解得a1=2.所以数列{a n}是首项为2、公比为2的等比数列，所以a n=2n.(2)由(1)得1na=12n，所以T n=12+212+…+12n=111-2211-2n⎡⎤⎛⎫⎢⎥⎪⎝⎭⎢⎥⎣⎦=1-12n.等差、等比数列的综合问题例4(2021·南通二调)设{a n}是公差为d的等差数列，{b n}是公比为q(q≠1)的等比数列，记c n=a n+b n.(1)求证：数列{c n+1-c n-d}为等比数列；(2)已知数列{c n}的前4项分别为4，10，19，34，求数列{a n}和{b n}的通项公式.【解答】(1)由题意得c n+1-c n-d=(a n+1+b n+1)-(a n+b n)-d=(a n+1-a n)-d+(b n+1-b n)=b n(q-1)≠0，从而211----n nn nc c dc c d+++=1(-1)(-1)nnb qb q+=q.又由于c2-c1-d=b1(q-1)≠0，所以{c n+1-c n-d}是首项为b1(q-1)，公比为q的等比数列.(2)方法一：{c n+1-c n-d}的前3项为6-d，9-d，15-d，则(9-d)2=(6-d)(15-d)，解得d=3，从而q=2.又由于111143210a ba b+=⎧⎨++=⎩，，解得a1=1，b1=3，所以a n=3n-2，b n=3·2n-1.方法二：由题意得1111211311410219334a ba db qa db qa db q+=⎧⎪++=⎪⎨++=⎪⎪++=⎩，，，，消去a1，得112113211-6-9-15d b q bd b q b qd b q b q+=⎧⎪+=⎨⎪+=⎩，，，消去d，得211132111-23-26b q b q bb q b q b q⎧+=⎨+=⎩，，消去b1，得q=2，从而解得a1=1，b1=3，d=3.所以a n=3n-2，b n=3·2n-1.【精要点评】等差数列与等比数列的综合运用主要还是考查基本量的运算，同时考查同学综合分析问题的力量.变式(2021·北京卷)已知等差数列{a n}满足a1+a2=10，a4-a3=2.(1)求数列{a n}的通项公式；(2)设等比数列{b n}满足b2=a3，b3=a7，问：b6与数列{a n}的第几项相等?【解答】(1)设等差数列{a n}的公差为d.由于a4-a3=2，所以d=2.又由于a1+a2=10，所以2a1+d=10，解得a1=4.所以a n=4+2(n-1)=2n+2.(2)设等比数列{b n}的公比为q.由于b2=a3=8，b3=a7=16，所以q=2，b1=4.所以b6=4×26-1=128.由128=2n+2，得n=63.所以b6与数列{a n}的第63项相等.1.(2021·泰州二模)在等比数列{a n}中，已知a3=4，a7-2a5-32=0，则a7=.【答案】64【解析】设公比为q，则有a3q4-2a3q2-32=0，即q4-2q2-8=0，解得q2=4(负值舍去)，所以a7=a3q4=64.2.在正项等比数列{a n}中，若a3a11=16，则log2a2+log2a12=.【答案】4【解析】由于等比数列{a n}中，a3a11=16，所以a2a12=a3a11=16，所以log2a2+log2a12=log2(a2a12)=log216=4.3.在等比数列{a n}中，若S5=4，S10=12，则S15=.【答案】28【解析】由等比数列的性质知S5，S10-S5，S15-S10成等比数列，S5=4，S10-S5=8，所以S15-S10=16，则S15=28.4.(2022·苏北四市期中)在等比数列{a n}中，若a1=1，a3a5=4(a4-1)，则a7=.【答案】4【解析】由题知a3a5=4(a4-1)=24a，得a4=2，又a1=1，所以由24a=a1·a7，得a7=4.5.(2021·安徽卷)已知数列{a n}是递增的等比数列，且a1+a4=9，a2a3=8.(1)求数列{a n}的通项公式；(2)设S n为数列{a n}的前n项和，b n=11nn naS S++，求数列{b n}的前n项和T n.【解答】(1)由题设知a1a4=a2a3=8，联立a1+a4=9，解得1418aa=⎧⎨=⎩，或1481aa=⎧⎨=⎩，(舍去).由a4=a1q3，得公比q=2，所以a n=a1q n-1=2n-1.(2)S n=1(1-)1-na qq=2n-1，又b n=11nn naS S++=11-n nn nS SS S++=1nS-11nS+，所以T n=b1+b2+…+b n=1211-S S⎛⎫⎪⎝⎭+2311-S S⎛⎫⎪⎝⎭+…+（1nS-11nS+）=11S-11nS+=1-112-1n+.趁热打铁，事半功倍.请老师布置同学们完成《配套检测与评估》中的练习第79~80页.【检测与评估】第40课等比数列一、填空题1.(2021·全国卷)若等比数列{a n}满足a1=14，a3a5=4(a4-1)，则a2=.2.在等比数列{a n}中，S n为其前n项和，已知a5=2S4+3，a6=2S5+3，那么此数列的公比q=.3.(2021·湖南卷)设S n为等比数列{a n}的前n项和，若a1=1，且3S1，2S2，S3成等差数列，则a n=.4.若方程x2-5x+m=0与x2-10x+n=0的四个根适当排列后，恰好组成一个首项为1的等比数列，则m∶n值为.5.(2021·泰州期末)在等比数列{a n}中，若a1+32a6=0，a3a4a5=1，则数列的前6项和为.6.(2021·镇江期末)设等比数列{a n}的前n项和为S n，若S3=7，S6=63，则a7+a8+a9=.7.若等比数列{a n}的各项均为正数，且a10a11+a9a12=2e5，则ln a1+ln a2+…+ln a20=.8.已知a n=1n sinπ25n，S n=a1+a2+…+a n，那么在S1，S2，…，S100中，正数的个数是.二、解答题9.(2022·福建卷)在等比数列{a n}中，已知a2=3，a5=81.(1)求数列{a n}的通项公式；(2)设b n=log3a n，求数列{b n}的前n项和S n.10.(2021·苏州调查)已知数列{a n}共有2k项(k≥2，k∈N*)，数列{a n}的前n项和为S n，满足a1=2，a n+1=(p-1)S n+2(n=1，2，…，2k-1)，其中常数p>1.(1)求证：数列{a n}是等比数列；(2)若p=22-12k，数列{bn}满足b n=1n log2(a1a2…a n)(n=1，2，…，2k)，求数列{b n }的通项公式.11.(2021·湖南卷)设数列{a n}的前n项和为S n，已知a1=1，a2=2，且a n+2=3S n-S n+1+3，n∈N*.(1)求证：a n+2=3a n；(2)求S n.三、选做题(不要求解题过程，直接给出最终结果)12.(2021·桐乡一中)在数列{a n}中，S n为它的前n项和，已知a2=4，a3=15，且数列{a n+n}是等比数列，则S n=.13.已知数列{a n}满足a1=1，a n+1·a n=2n(n∈N*)，则S2 017=.【检测与评估答案】第40课等比数列1.12 【解析】由于{a n }为等比数列，所以a 3a 5=4(a 4-1)=24a ，得a 4=2.又a 1=4114a a ，=214=8=q 3，得公比q=2，所以a 2=14×2=12.2.3 【解析】由a 5=2S 4+3，a 6=2S 5+3，两式相减得a 6-a 5=2a 5，得a 6=3a 5，所以公比q=3.3.3n-1 【解析】设等比数列{a n }的公比为q.由3S 1，2S 2，S 3成等差数列，得4S 2=3S 1+S 3，即3S 2-3S 1=S 3-S 2，所以3a 2=a 3，得公比q=3，所以a n =a 1q n-1=3n-1.4.14 【解析】设方程x 2-5x+m=0的两根为x 1，x 2，方程x 2-10x+n=0的两根为x 3，x 4，则34123412105··x x x x x x n x x m +=+=⎧⎧⎨⎨==⎩⎩，，，，由题意知x 1=1，x 2=4，x 3=2，x 4=8，所以m=4，n=16，所以m ∶n=14.5.-214 【解析】由a 1+32a 6=0，得61a a =-132=q 5，所以q=-12.又a 3a 4a 5=1，即34a =1，所以a 4=1，则a 1=43a q =-8，所以{a n }的前6项和S 6=61-81--2112⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+=-214.6.448 【解析】由于a 1+a 2+a 3=7，a 1+a 2+a 3+…+a 6=63，所以a 4+a 5+a 6=56.由于a 1+a 2+a 3，a 4+a 5+a 6，a 7+a 8+a 9成等比数列，所以a 7+a 8+a 9=2567=448.7.50 【解析】由题意得2a 10a 11=2e 5⇒a 10a 11=e 5，所以ln a 1+ln a 2+…+lna 20=ln(a 1·a 2·…·a 20)=ln(a 10a 11)10=10×ln e 5=50.8. 100 【解析】当1≤n ≤24时，a n >0；当26≤n ≤49时，a n <0，但其确定值要小于1≤n ≤24时相应的值；当51≤n ≤74时，a n >0；当76≤n ≤99时，a n <0，但其确定值要小于51≤n ≤74时相应的值.所以当1≤n ≤100时，均有S n >0.9.(1)设等比数列{a n }的公比为q.依题意得141381a q a q =⎧⎨=⎩，，解得113a q =⎧⎨=⎩，， 所以a n =3n-1.(2)由于b n =log 3a n =n-1，所以S n =1()2n n b b +=2-2n n .10. (1) 由于a n+1=(p-1)S n +2(n=1，2，…，2k-1)，所以a n =(p-1)S n -1+2 (n=2，3，…，2k )， 则当n=2，3，…，2k-1时，两式相减，得a n+1-a n =(p-1)(S n -S n -1)，即a n+1-a n =(p-1)a n . 所以a n+1=pa n (n=2，3，…，2k-1).原式中，令n=1，得a 2=(p-1)a 1+2=2(p-1)+2=2p=pa 1.所以a n+1=pa n ，即1n n a a +=p ≠0(n=1，2，…，2k-1). 所以数列{a n }是等比数列. (2) 由(1)得a n =a 1p n-1.所以b n =1n log 2(a 1a 2…a n ) =1n log 2(a 1·a 1p ·a 1p 2·…·a 1p n-1) =1n log 2(1n a ·12-1n p +++)=log 2(a 1·-12n p)=1+-12n log 2p=1+-12n·22-1k=1+-1 2-1 n k.11. (1) 由于对任意的n∈N*，有a n+2=3S n-S n+1+3，所以对任意的n∈N*，n≥2，有a n+1=3S n-1-S n+3.两式相减，得a n+2-a n+1=3a n-a n+1，即a n+2=3a n，n≥2.又由于a1=1，a2=2，所以a3=3S1-S2+3=3a1-(a1+a2)+3=3a1.所以对一切n∈N*，a n+2=3a n.(2) 由(1)知，a n≠0，所以2nnaa+=3，于是数列{a2n-1}是首项a1=1，公比为3的等比数列；数列{a2n}是首项a2=2，公比为3的等比数列.因此a2n-1=3n-1，a2n=2×3n-1.于是S2n=a1+a2+…+a2n=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)=(1+3+…+3n-1)+2×(1+3+…+3n-1)=3×(1+3+…+3n-1)=3(3-1)2n⨯，从而S2n-1=S2n-a2n=3(3-1)2n⨯-2×3n-1=32×(5×3n-2-1).综上，S n=-3223(53-1)23(3-1).2nnnn⎧⨯⨯⎪⎪⎨⎪⨯⎪⎩，为奇数，，为偶数12.3n-222n n++【解析】由于{a n+n}是等比数列，所以q=3232aa++=3，a2+2=6，所以a n+n=6×3n-2=2×3n-1，所以a n=2×3n-1-n，S n=2(1-3)1-3n-(1)2n n+=3n-222n n++.13.21 010-3【解析】依据题意，a2=2，由a n+1·a n=2n(n∈N*)，得a n+2·a n+1=2n+1，两式相除得2nnaa+=2，所以数列的奇数项和偶数项分别成等比数列，而数列的前2 017项中有1 009项奇数项和1 008项偶数项，而且奇数项和偶数项构成的数列分别是以1和2为首项，以2为公比的等比数列，所以S2017=10091-21-2+10082(1-2)1-2=21 010-3.。

2021版高考北师大版文科数学一轮复习单元评估检测（四）（第九章）含解析温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例,答案解析附后。

关闭Word文档返回原板块.单元评估检测（四）（第九章）（120分钟150分)一、选择题(本大题共12小题，每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列结论正确的是()A.各个面都是三角形的几何体是三棱锥B。

以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥C。

棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线【解析】选D。

A错误.如图①所示,由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形,但它不是棱锥。

B错误.如图②，若△ABC不是直角三角形或是直角三角形,但旋转轴不是直角边所在直线,所得的几何体都不是圆锥。

C错误。

由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.D正确。

2.设x，y,z是空间不同的直线或平面，对下列四种情形：①x，y，z均为直线;②x,y是直线,z是平面；③z是直线,x,y是平面；④x，y,z均为平面。

其中使“x⊥z且y⊥z⇒x∥y"为真命题的是（)A。

③④B.①③ C.②③D。

①②【解析】选C.由正方体模型可知①④为假命题；由线面垂直的性质定理可知②③为真命题。

3.如图，正方体ABCD—A1B1C1D1中，E为棱BB1的中点，用过点A，E,C1的平面截去该正方体的下半部分,则剩余几何体的主视图是()【解析】选A.正方体ABCD-A1B1C1D1中,过点A,E,C1的平面截去该正方体的下半部分后,剩余部分的直观图如图:则该几何体的主视图为选项A.4.关于空间两条直线a，b和平面α，下列命题正确的是() A。

若a∥b,bα，则a∥αB。

若a∥α,bα,则a∥bC。

2021届江苏高三数学新高考模拟卷4（原卷版）一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．若集合A ={x ∈N||x −1|≤1 }, B ={x|y =√1−x 2}，则A ∩B 的真子集的个数为（ ） A ．3 B ．4C ．7D ．82． 已知1xi+＝1－yi ，其中x ，y 是实数，i 是虚数单位，则x －y ＝( ) A ．1B ．2C ．3D ．43． “θ为第一或第四象限角”是“cos 0θ>”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．如图是函数()y f x =的导函数()'y f x =的图象,则下列说法正确的是( )A ．x a =是函数()y f x =的极小值点B ．当x a =-或x b =时,函数()f x 的值为0C ．函数()y f x =关于点()0,c 对称D ．函数()y f x =在(),b +∞上是增函数5．一个放射性物质不断衰变为其他物质，每经过一年就有34的质量发生衰变,剩余质量为原来的14.若该物质余下质量不超过原有的1%，则至少需要的年数是（ ） A ．3B ．4C ．5D ．66．已知向量()()4,1,5,2a b =-=-且()()//a b ma b +-，则m = A ．1B ．1-C ．75D ．75-7．已知函数()f x 是定义域在R 上的偶函数，且()()11f x f x =+-，当[]0,1x ∈时，()3f x x =，则关于x 的方程()cos f x x π=在15,22⎡⎤-⎢⎥⎣⎦上所有实数解之和为（ ）A ．1B ．3C ．6D ．78．已知随机变量X 的分布列是：当a 变化时，下列说法正确的是（ ） A ．E (X )，D (X )均随着a 的增大而增大 B ．()(),E X D X 均随着a 的增大而减小C ．E (X )随着a 的增大而增大，D (X )随着a 的增大而减小 D ．E (X )随着a 的增大而减小(),D X 随着a 的增大而增大二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得3分.9．如图，在四面体ABCD 中，截面PQMN 是正方形，则在下列命题中，正确的为（ ）A ．AC BD ⊥B ．//AC 截面PQMN C ．AC BD =D ．异面直线PM 与BD 所成的角为45︒A ．函数3y x =是圆O 的一个太极函数B ．圆O 的所有非常数函数的太极函数都不能为偶函数C ．函数sin y x =是圆O 的一个太极函数D ．函数()f x 的图象关于原点对称是()f x 为圆O的太极函数的充要条件11．已知抛物线C ：()220y px p =>的准线经过点()1,1M -，过C 的焦点F 作两条互相垂直的直线1l ，2l ，直线1l 与C 交于A ，B 两点，直线2l 与C 交于D ，E 两点，则下列结论正确的是（ ）A ．2p =B ．AB DE +的最小值为16C ．四边形ADBE 的面积的最小值为64D ．若直线1l 的斜率为2，则90AMB ∠=︒12．古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点,A B 的距离之比为定值()1λλ≠的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系xOy 中,()()2,0,4,0,A B -点12PA P PB=满足.设点P 的轨迹为C ,下列结论正确的是（ ） A ．C 的方程为()2249x y ++=B ．在x 轴上存在异于,A B 的两定点,D E ,使得12PD PE=C ．当,,A B P 三点不共线时,射线PO 是APB ∠的平分线D ．在C 上存在点M ,使得2||MO MA =三、填空题（本题共4小题，每小题5分，其中第16题分值分配为前3分、后2分，满分共20分）13．已知2()⎛= ⎝nf x x x 的展开式中第三项的二项式系数为15，则n =__________，该展开式中常数项为__________.14．函数2()ln f x x ax x =-在2(,2)e上不单调，则实数a 的取值范围是_____．15．已知过点(10)， 的直线与抛物线2x y = 交于A 、B 两点，线段AB 的垂直平分线经过点(0)2，，F 为抛物线的焦点，则||||AF BF += __________．16．设n S 是数列{}n a 的前n 项和，若1(1)2nn n n S a =-+，则1211S S S ++⋯+=_____.四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤.17．(本题10分) 已知在ABC 中，角A 、B 、C 的对边分别为a 、b 、c，且满足cossin ,2B Ca B a +== （1）求角A 的大小；（2）若点M 为边AC 边上一点，且,2MC MB ABM π=∠=，求ABC 的面积．18．(本题10分) 已知{}n a 是递增的等比数列，11a =，且22a 、332a 、4a 成等差数列.（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）设21231log log n n n b a a ++=⋅，n *∈N ，求数列{}n b 的前n 项和n S .19．(本题12分) 《山东省高考改革试点方案》规定：从2017年秋季高中入学的新生开始，不分文理科；2020年开始，高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成．将每门选考科目的考生原始成绩从高到低划分为A 、B +、B 、C +、C 、D +、D 、E 共8个等级．参照正态分布原则，确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%．选考科目成绩计入考生总成绩时，将A 至E 等级内的考生原始成绩，依照等比例转换法则，分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间，得到考生的等级成绩．某校高一年级共2000人，为给高一学生合理选科提供依据，对六个选考科目进行测试，其中物理考试原始成绩基本服从正态分布(60,169)N ．（1）求物理原始成绩在区间(47,86)的人数；（2）按高考改革方案，若从全省考生中随机抽取3人，记X 表示这3人中等级成绩在区间[61,80]的人数，求X 的分布列和数学期望． （附：若随机变量()2~,N ξμσ，则()0.682P μσξμσ-<<+=，(22)0.954P μσξμσ-<<+=，(33)0.997P μσξμσ-<<+=）20．(本题12分) 已知过圆1C ：221x y +=上一点1,22E ⎛ ⎝⎭的切线，交坐标轴于A 、B 两点，且A 、B 恰好分别为椭圆2C ：()222210x y a b a b+=>>的上顶点和右顶点.（1）求椭圆2C 的方程；（2）已知P 为椭圆的左顶点，过点P 作直线PM 、PN 分别交椭圆于M 、N 两点，若直线MN 过定点()1,0Q -，求证：PM PN ⊥.21．(本题13分) 如图，四棱锥P ABCD -，四边形ABCD 为平行四边形，AD BD ⊥，ACBD O =，2AD BD ==，PB PD ⊥，PB PD =，PA PC =，M 为PD 中点.（1）求证：//OM 平面PBC ； （2）求证：平面PAD ⊥平面PBD ； （3）求二面角A PB C --的余弦值.22．(本题13分)已知函数()()()ln ,1f x x g x ax a R ==-∈（1）讨论函数()()()h x f x g x =-的单调性；（2）若函数()f x 与()g x 的图象有两个不同的交点()()112212),(,, A x y B x y x x < （i ）求实数a 的取值范围（ii ）求证：110,y -<<且122(y ye e e +>为自然对数的底数).。

江苏省连云港市2021届新高考数学四模考试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

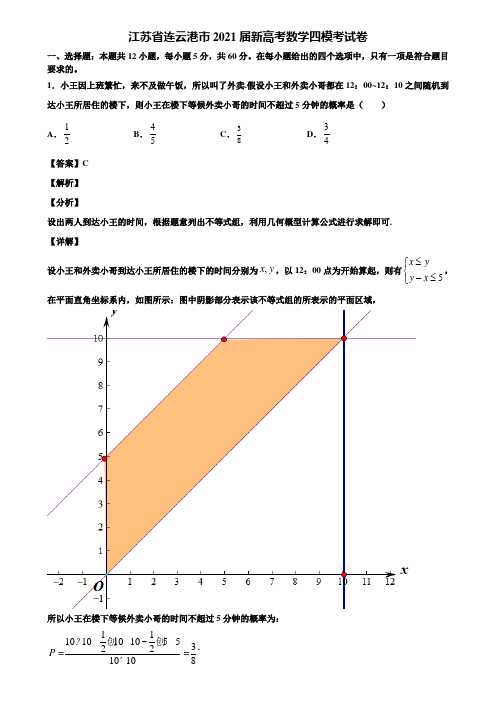
1．小王因上班繁忙，来不及做午饭，所以叫了外卖.假设小王和外卖小哥都在12：00~12：10之间随机到达小王所居住的楼下，则小王在楼下等候外卖小哥的时间不超过5分钟的概率是（ ） A ．12B ．45C ．38D ．34【答案】C 【解析】 【分析】设出两人到达小王的时间，根据题意列出不等式组，利用几何概型计算公式进行求解即可. 【详解】设小王和外卖小哥到达小王所居住的楼下的时间分别为,x y ，以12：00点为开始算起，则有5x yy x ≤⎧⎨-≤⎩，在平面直角坐标系内，如图所示：图中阴影部分表示该不等式组的所表示的平面区域，所以小王在楼下等候外卖小哥的时间不超过5分钟的概率为：11101010105532210108P ?创-创==´.故选：C 【点睛】本题考查了几何概型中的面积型公式，考查了不等式组表示的平面区域，考查了数学运算能力.2．设a r ，b r是非零向量，若对于任意的R λ∈，都有a b a b λ-≤-r r r r 成立，则A ．//a bB ．a b ⊥v vC ．()-⊥r r r a b aD ．()-⊥a b b rr r【答案】D 【解析】 【分析】画出a r，b r，根据向量的加减法，分别画出()a b λ-rr的几种情况，由数形结合可得结果. 【详解】由题意，得向量()a b -r r 是所有向量()a b λ-r r中模长最小的向量，如图，当AC BC ⊥，即()-⊥a b b r r r 时，||AC 最小，满足a b a b λ-≤-r r r r，对于任意的R λ∈，所以本题答案为D. 【点睛】本题主要考查了空间向量的加减法，以及点到直线的距离最短问题，解题的关键在于用有向线段正确表示向量，属于基础题.3．设O 为坐标原点，P 是以F 为焦点的抛物线()220y px p =>上任意一点，M 是线段PF 上的点，且2PM MF =,则直线OM 的斜率的最大值为( )A 3B ．23C 2D ．1【答案】C 【解析】试题分析：设200,)2y P y p （，由题意(,0)2p F ，显然00y <时不符合题意，故00y >，则 2001112()(,)3333633y y p OM OF FM OF FP OF OP OF OP OF p =+=+=+-=+=+u u u u r u u u r u u u u r u u u r u u u r u u u r u u u r u u u r u u ur u u u r ，可得：2000232263OM y k y p y p p y p ==≤=++，当且仅当22002,y p y ==时取等号，故选C ． 考点：1．抛物线的简单几何性质；2．均值不等式．【方法点晴】本题主要考查的是向量在解析几何中的应用及抛物线标准方程方程，均值不等式的灵活运用，属于中档题．解题时一定要注意分析条件，根据条件2PM MF =，利用向量的运算可知200(,)633y y p M p +，写出直线的斜率，注意均值不等式的使用，特别是要分析等号是否成立，否则易出问题．4．双曲线22:21C x y -=的渐近线方程为( ) A．0x ±= B ．20x y ±= C0y ±= D ．20x y ±=【答案】A 【解析】 【分析】将双曲线方程化为标准方程为22112y x -=，其渐近线方程为2212y x -=，化简整理即得渐近线方程. 【详解】双曲线22:21C x y -=得22112y x -=，则其渐近线方程为22012y x -=，整理得0x =. 故选：A 【点睛】本题主要考查了双曲线的标准方程，双曲线的简单性质的应用.5．如图，在矩形OABC 中的曲线分别是sin y x =，cos y x =的一部分，,02A π⎛⎫⎪⎝⎭，()0,1C ，在矩形OABC内随机取一点，若此点取自阴影部分的概率为1P ，取自非阴影部分的概率为2P ，则（ ）A ．12P P <B ．12P P >C ．12P P =D ．大小关系不能确定【答案】B 【解析】 【分析】先用定积分求得阴影部分一半的面积，再根据几何概型概率公式可求得． 【详解】根据题意，阴影部分的面积的一半为：()4cos sin 21x x dx π-=⎰，于是此点取自阴影部分的概率为)()12142141.41122 3.22P ππ-=⨯=>=． 又21112P P =-<，故12P P >． 故选B ． 【点睛】本题考查了几何概型，定积分的计算以及几何意义，属于中档题．6．已知直线l ：310kx y k --+=与椭圆22122:1(0)x yC a b a b+=>>交于A 、B 两点，与圆2C ：()()22311x y -+-=交于C 、D 两点.若存在[]2,1k ∈--，使得AC DB =u u u r u u u r ，则椭圆1C 的离心率的取值范围为（ ）A ．36,33⎣⎦B ．33C ．3D ．63【答案】A 【解析】 【分析】由题意可知直线过定点即为圆心，由此得到,A B 坐标的关系，再根据点差法得到直线的斜率k 与,A B 坐标的关系，由此化简并求解出离心率的取值范围. 【详解】设()()1122,,,A x y B x y ，且线:310l kx y k --+=过定点()3,1即为2C 的圆心，因为AC DB =u u u r u u u r，所以1212236212C D C D x x x x y y y y +=+=⨯=⎧⎨+=+=⨯=⎩，又因为2222221122222222b x a y a b b x a y a b ⎧+=⎨+=⎩，所以()()2222221212b x x a y y -=--， 所以2121221212y y x x b x x a y y -+=-⋅-+，所以[]2232,1b k a=-∈--，所以2212,33b a ⎡⎤∈⎢⎥⎣⎦，所以22212,33a c a -⎡⎤∈⎢⎥⎣⎦，所以()2121,33e ⎡⎤-∈⎢⎥⎣⎦，所以33e ∈⎣⎦.故选：A. 【点睛】本题考查椭圆与圆的综合应用，着重考查了椭圆离心率求解以及点差法的运用，难度一般.通过运用点差法达到“设而不求”的目的，大大简化运算.7．《聊斋志异》中有这样一首诗：“挑水砍柴不堪苦，请归但求穿墙术.得诀自诩无所阻，额上坟起终不悟.”在这里，我们称形如以下形式的等式具有“穿墙术”：====，则按照以上规律，若=“穿墙术”，则n =（ ）A ．48B ．63C ．99D ．120【答案】C 【解析】 【分析】观察规律得根号内分母为分子的平方减1，从而求出n. 【详解】解：观察各式发现规律，根号内分母为分子的平方减1 所以210199n =-= 故选：C. 【点睛】本题考查了归纳推理，发现总结各式规律是关键，属于基础题.8．若[]x 表示不超过x 的最大整数(如[]2.52=，[]44=，[]2.53-=-)，已知2107n n a ⎡⎤=⨯⎢⎥⎣⎦，11b a =，()*110,2n n n b a a n n -=-∈≥N ，则2019b =（ ）A ．2B ．5C ．7D ．8【答案】B 【解析】 【分析】求出1b ，2b ，3b ，4b ，5b ，6b ，判断出{}n b 是一个以周期为6的周期数列，求出即可． 【详解】解：2107n n a ⎡⎤=⨯⎢⎥⎣⎦.*111(102)n n n b a b a a n n --∈≥N ＝，＝，，∴112027[]a b ＝＝＝，2200[287]a ＝＝， 2281028b -⨯＝＝，同理可得：332855a b ＝，＝；4428577a b ＝，＝；55285711a b ＝，＝.662857144a b ＝，＝；72857142a ＝，72b ＝，…….∴6n n b b +＝.故{}n b 是一个以周期为6的周期数列， 则20196336335b b b ⨯+＝＝＝. 故选：B. 【点睛】本题考查周期数列的判断和取整函数的应用．9．如图所示，正方体1111ABCD A B C D -的棱AB ，11A D 的中点分别为E ，F ，则直线EF 与平面11AA D D 所成角的正弦值为（ ）A 5B ．30C 6 D 25【答案】C 【解析】 【分析】以D 为原点，DA ，DC ，DD 1 分别为,,x y z 轴，建立空间直角坐标系，由向量法求出直线EF 与平面AA 1D 1D 所成角的正弦值． 【详解】以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，设正方体ABCD ﹣A 1B 1C 1D 1的棱长为2，则()2,1,0E ，()1,0,2F ，()1,1,2EF =--u u u v， 取平面11AA D D 的法向量为()0,1,0n =r，设直线EF 与平面AA 1D 1D 所成角为θ，则sinθ＝|6cos ,|6EF n EF n EF n ⋅==⋅u u u v ru u u v r u u u v r， ∴直线EF 与平面11AA D D 所成角的正弦值为6.故选C ．【点睛】本题考查了线面角的正弦值的求法，也考查数形结合思想和向量法的应用，属于中档题． 10．在ABC V 中，点P 为BC 中点，过点P 的直线与AB ，AC 所在直线分别交于点M ，N ，若AM AB λ=u u u u r u u u r ，(0,0)AN AC μλμ=>>u u ur u u u r ，则λμ+的最小值为（ ）A ．54B ．2C ．3D ．72【答案】B 【解析】 【分析】由M ，P ，N 三点共线，可得11122λμ+=，转化11()22λμλμλμ⎛⎫+=++ ⎪⎝⎭，利用均值不等式，即得解. 【详解】因为点P 为BC 中点，所以1122AP AB AC =+u u u r u u u r u u u r，又因为AM AB λ=u u u u r u u u r ，AN AC μ=u u ur u u u r ，所以1122AP AM ANλμ=+u u u r u uu u r u u u r．因为M，P，N三点共线，所以11122λμ+=，所以111111()122222222λμλμλμλμλμμλμλ⎛⎫⎛⎫+=++=++++⨯⋅=⎪ ⎪⎝⎭⎝⎭…，当且仅当,11122λμμλλμ⎧=⎪⎪⎨⎪+=⎪⎩即1λμ==时等号成立，所以λμ+的最小值为1．故选：B【点睛】本题考查了三点共线的向量表示和利用均值不等式求最值，考查了学生综合分析，转化划归，数学运算的能力，属于中档题.11．如下的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b分别为176，320，则输出的a为（）A．16 B．18 C．20 D．15【答案】A【解析】【分析】根据题意可知最后计算的结果为a b，的最大公约数.【详解】输入的a，b分别为176,320,根据流程图可知最后计算的结果为a b，的最大公约数，按流程图计算320-176=144,176-144=32,144-32=112,112-32=80,80-32=48,48-32=16,32-16=16,易得176和320的最大公约数为16， 故选:A. 【点睛】本题考查的是利用更相减损术求两个数的最大公约数,难度较易.12．二项式22)nx+的展开式中只有第六项的二项式系数最大，则展开式中的常数项是( ) A ．180 B ．90C ．45D ．360【答案】A 【解析】试题分析：因为22)nx+的展开式中只有第六项的二项式系数最大，所以10n =，551021101022•?()2r r rr r rr T C C x x--+==，令5502r -=，则2r =，23104180T C ==.考点：1.二项式定理；2.组合数的计算.二、填空题：本题共4小题，每小题5分，共20分。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

核心考点·精准研析考点一条件概率、事件的独立性1.市场调查发现,大约的人喜欢在网上购买家用小电器,其余的人则喜欢在实体店购买家用小电器.经工商局抽样调查发现网上购买的家用小电器合格率约为,而实体店里的家用小电器的合格率约为.现工商局12315电话接到一个关于家用小电器不合格的投诉,则这台被投诉的家用小电器是在网上购买的可能性是( )A. B. C. D.2.甲、乙、丙、丁四名同学报名参加假期社区服务活动,社区服务活动共有关怀老人、环境监测、教育咨询、交通宣传四个项目,每人限报其中一项,记事件A为“4名同学所报项目各不相同”,事件B为“只有甲同学一人报关怀老人项目”,则P(A|B)的值为( )A. B.C. D.3.甲、乙两人玩投篮游戏,规则如下:两人轮流投篮,每人至多投2次,甲先投,若有人投中即停止投篮,结束游戏,已知甲每次投中的概率为,乙每次投中的概率为,求:乙投篮次数不超过1次的概率.世纪金榜导学号【解析】1.选A.不合格小电器在网上购买的概率为×=,不合格小电器在实体店购买的概率为×=,所以这台被投诉的家用小电器是在网上购买的可能性是=.2.选C.因为P(B)=,P(AB)=,所以P(A|B)==.3.记“甲投篮投中”为事件A,“乙投篮投中”为事件B.“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中,再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,所求的概率是P=P(A+·B+··A)=P(A)+P(·B)+P(··A)=P(A)+P()·P(B)+P()·P()·P(A)=+×+××=.所以乙投篮次数不超过1次的概率为.1.条件概率的3种求法定义法先求P(A)和P(AB),再由P(B|A)=求P(B|A)基本事件法借助古典概型概率公式,先求事件A包含的基本事件数n(A),再求事件AB所包含的基本事件数n(AB),得P(B|A)=缩样法缩小样本空间的方法,就是去掉第一次抽到的情况,只研究剩下的情况,用古典概型求解,它能化繁为简2.相互独立事件同时发生的概率的两种求法(1)直接法:利用相互独立事件的概率乘法公式.(2)间接法:从对立事件入手计算.考点二n次独立重复试验、二项分布【典例】1.种植某种树苗,成活率为0.9.若种植这种树苗5棵,则恰好成活4棵的概率约为( )A.0.33B.0.66C.0.5D.0.452.某气象站天气预报的准确率为80%,计算:(结果保留到小数点后2位)(1)5次预报中恰有2次准确的概率.(2)5次预报中至少有2次准确的概率.(3)5次预报中恰有2次准确,且其中第3次预报准确的概率. 【解题导思】序号联想解题1种5棵成活4棵联想到n次独立重复试验恰好发生k次的概率公式2 (1)联想到用公式p k(2)由“至少2次”联想到对立事件“最多1次”,即0次,1次(3)转化为4次独立重复试验恰好发生1次试验模型【解析】1.选A.根据n次独立重复试验中,事件A恰好发生k次的概率公式得到种植这种树苗5棵,则恰好成活4棵的概率为0.94(1-0.9)≈0.33.2.令X表示5次预报中预报准确的次数,则X～B5,,故其分布列为P(X=k)=k1-5-k(k=0,1,2,3,4,5).(1)“5次预报中恰有2次准确”的概率为P(X=2)=2×1-3=10××≈0.05.(2)“5次预报中至少有2次准确”的概率为P(X≥2)=1-P(X=0)-P(X=1)=1-×0×1-5-××1-4=1-0.000 32-0.006 4≈0.99. (3)“5次预报中恰有2次准确,且其中第3次预报准确”的概率为××1-3×≈0.02.1.熟记概率公式n次独立重复试验中事件A恰好发生k次的概率为p k(1-p)n-k.2.判断某随机变量是否服从二项分布的关键点(1)在每一次试验中,事件发生的概率相同.(2)各次试验中的事件是相互独立的.(3)在每一次试验中,试验的结果只有两个,即发生与不发生.1.位于坐标原点的一个质点P按下述规则移动:质点每次移动一个单位,移动的方向为向上或向右,并且向上、向右移动的概率都是,质点P移动五次后位于点(2,3)的概率是( )A. B. C. D.【解析】选B.如图,由题可知,质点P必须向右移动2次,向上移动3次才能位于点(2,3),问题相当于5次重复试验向右恰好发生2次的概率.所求概率为P=×2×3=×5=.2.设随机变量ξ～B(2,p),η～B(4,p),若P(ξ≥1)=,则P(η≥1)=________.【解析】P(ξ≥1)=1-P(ξ<1)=1-p0·(1-p)2=,所以p=,P(η≥1)=1-P(η=0)=1-04=1-=.答案:3.在一次数学考试中,第14题和第15题为选做题.规定每位考生必须且只需在其中选做一题.设4名考生选做这两题的可能性均为.设这4名考生中选做第15题的学生数为ξ,求ξ的分布列.【解析】随机变量ξ的可能取值为0,1,2,3,4,且ξ～B4,.所以P(ξ=k)=k1-4-k=4(k=0,1,2,3,4).所以变量ξ的分布列为ξ0 1 2 3 4P考点三正态分布命题精解读考什么:(1)正态曲线的应用.(2)正态分布与统计的综合应用.怎么考:正态分布作为考查数学应用意识的重要载体,在高考题中经常出现,试题常以选择题、填空题形式出现.学霸好方法巧用正态曲线的性质解题(1)正态曲线关于直线x=μ对称,用此性质可以进行灵活转化.(2)正态曲线与x轴之间的面积是1.正态曲线的应用【典例】1.已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,则P(-2≤ξ≤2)= ( )A.0.447B.0.628C.0.954D.0.9772.为了了解某地区高三男生的身体发育状况,抽查了该地区1 000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5 kg小于等于62.5 kg属于正常情况,则这1 000名男生中属于正常情况的人数是( )A.997B.954C.819D.683【解析】1.选C.因为随机变量ξ服从标准正态分布N(0,σ2), 所以正态曲线关于直线x=0对称.又P(ξ>2)=0.023,所以P(ξ<-2)=0.023.所以P(-2≤ξ≤2)=1-2×0.023=0.954.2.选D.由题意,可知μ=60.5,σ=2,所以P(58.5<X<62.5)=P(μ-σ<X<μ+σ)≈0.683,从而属于正常情况的人数是1 000×0.683≈683.如何利用正态曲线的性质解题?提示:充分利用正态曲线的对称性及正态曲线与x轴之间的面积为1.①正态曲线关于直线x=μ对称,从而在关于x=μ对称的区间上概率相等.②P(X<a)=1-P(X≥a),P(X≤μ-a)=P(X≥μ+a).3σ原则的应用【典例】1.在如图所示的矩形中随机投掷30 000个点,则落在曲线C 下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )附:正态变量在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)内取值的概率分别是0.683,0.954,0.997.A.4 985B.8 185C.9 970D.24 5582.工厂制造的某机械零件尺寸X服从正态分布N4,,问在一次正常的试验中,取1 000个零件时,不属于区间(3,5]这个尺寸范围的零件大约有多少个? 世纪金榜导学号【解析】1.选B.由题意P(0<X<3)=P(0<X≤2)+P(2<X<3)=0.683+(0.954-0.683)=0.818 5,所以落在曲线C下方的点的个数的估计值为30 000×=8 185.2.因为X～N4,,所以μ=4,σ=.所以不属于区间(3,5]的概率为P(X≤3)+P(X>5)=1-P(3<X≤5)=1-P(4-1<X≤4+1)=1-P(μ-3σ<X≤μ+3σ)≈1-0.997=0.003,所以1 000×0.003=3个,即不属于区间(3,5]这个尺寸范围的零件大约有3个.正态分布与统计的交汇问题【典例】近年来“双十一”已成为中国电子商务行业的年度盛事,并且逐渐影响到国际电子商务行业.某商家为了准备今年“双十一”的广告策略,随机调查了1 000名客户在去年“双十一”前后10天内网购所花时间T(单位:时),并将调查结果绘制成如图所示的频率分布直方图.由频率分布直方图可以认为,这10天网购所花的时间T近似服从N(μ,σ2),其中μ用样本平均值代替,σ2=0.24.(1)计算μ,并利用该正态分布求P(1.51<T<2.49).(2)利用由样本统计获得的正态分布估计整体,将这10天网购所花时间在(2,2.98)小时内的人定义为目标客户,对目标客户发送广告提醒.现若随机抽取10 000名客户,记X为这10 000人中目标客户的人数. (ⅰ)任取一人,求该人是目标客户的概率;(ⅱ)问:10 000人中目标客户的人数X为何值时概率最大?附:若随机变量Z服从正态分布N(μ,σ2),则P(μ-σ<Z<μ+σ)≈0.683,P(μ-2σ<Z<μ+2σ)≈0.954,P(μ-3σ<Z<μ+3σ)≈0.997,≈0.49. 世纪金榜导学号【解析】(1)μ=0.4×(0.050×0.8+0.225×1.2+0.550×1.6+0.825×2.0+0.600×2.4+0.200×2.8+0.050×3.2)=2,从而T服从N(2,0.24),又σ=≈0.49,从而P(1.51<T<2.49)=P(μ-σ<T<μ+σ)≈0.683.(2)(ⅰ)任意抽取1名客户,该客户是目标客户的概率为P(2<T<2.98)=P(μ<T<μ+2σ)=P(μ-2σ<T<μ+2σ)≈×0.954=0.477.(ⅱ)X服从B(10 000,0.477),P(X=k)=0.477k(1-0.477)10 000-k=0.477k·0.52310 000-k(k=0,1,2,…,10 000).设当X=k(k≥1,k∈N)时概率最大,则有得解得4 770-0.523<k<4 770+0.477,所以k=4 770.所以10 000人中目标客户的人数为4 770时概率最大.1.已知随机变量X服从正态分布N(3,σ2),则P(X<3)等于( )A. B. C. D.【解析】选D.由正态分布图象知,μ=3为该图象的对称轴,P(X<3)=P(X>3)=.2.随机变量X服从标准正态分布,则X的总体在区间(-3,3)内取值的概率为( ) A.0.998 B.0.997C.0.944D.0.841【解析】选B.标准正态分布N(0,1),σ=1,区间(-3,3),即(-3σ,3σ),概率P=0.997.1.设随机变量ξ服从正态分布N(1,σ2),则函数f(x)=x2+2x+ξ不存在零点的概率为 ( )A. B. C. D.【解析】选C.函数f(x)=x2+2x+ξ不存在零点,则Δ=4-4ξ<0,ξ>1,因为ξ～N(1,σ2),所以μ=1,P=.2.“过大年,吃水饺”是我国不少地方过春节的一大习俗.2019年春节前夕, A市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数 (同一组中的数据用该组区间的中点值作代表);(2)①由直方图可以认为,速冻水饺的该项质量指标值Z服从正态分布N(μ,σ2),利用该正态分布,求Z落在(14.55,38.45)内的概率;②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于(10,30)内的包数为X,求X 的分布列.附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为σ=≈11.95;②若Z～N(μ,σ2),则P(μ-σ<Z<μ+σ)≈0.683,P(μ-2σ<Z<μ+2σ)≈0.954.【解析】(1)所抽取的100包速冻水饺的该项质量指标值的样本平均数为=5×0.1+15×0.2+25×0.3+35×0.25+45×0.15=26.5.(2)①因为Z服从正态分布N(μ,σ2 ), μ=26.5,σ≈11.95,所以P(14.55<Z<38.45)=P(26.5-11.95<Z<26.5+11.95)≈0.683,所以Z落在区间(14.55,38.45)内的概率约为0.683.②根据题意得X～B4,,所以P(X=0)=4=,P(X=1)=4= ;P(X=2)=4= ;P(X=3)=4= ;P(X=4)=4=.所以X的分布列为X 0 1 2 3 4P关闭Word文档返回原板块快乐分享，知识无界！感谢您的下载!由Ruize收集整理！。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

滚动评估检测(二)(第一至第五章)(120分钟150分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={x|x2-1<0},B=,则A∩B= ( )A.(-1,1)B.(1,+∞)C. D.【解析】选D.A={x|x2-1<0}={x|-1<x<1},B=,所以A∩B=.2.“<1”是“>1”的( )A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件【解析】选A.由题意得,根据<1,解得x>0,又由>1,解得0<x<1,所以“<1”是“>1”的必要不充分条件.3.(2020·苏州模拟)已知向量a=(,1),b=(-3,),则向量b在向量a方向上的投影为( )A.-B.C.-1D.1【解析】选A.由投影的定义可知:向量b在向量a方向上的投影为:|b|·cos<a,b>,又因为a·b=|a|·|b|·cos<a,b>.所以|b|·cos<a,b>===-.4.设a=,b=,c=ln,则( )A.c<a<bB.c<b<aC.a<b<cD.b<a<c【解析】选B.由<1可得c=ln<0,由题意可得a>0,b>0,又因为函数f(x)=在区间(0,e)上单调递增,故f>f,即:>,则ln>ln,据此有:ln>ln,结合对数函数的单调性有:>,即a>b,综上可得:a>b>c.5.(2019·扬州模拟)已知向量a=(1,m),b=(m,1),则“m=1”是“a∥b”成立的 ( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】选A.向量a=(1,m),b=(m,1),若a∥b,则m2=1,即m=±1,所以“m=1”是“a∥b”的充分不必要条件.6.(2020·嘉兴模拟)函数y=sin x+sin2x的部分图象大致是 ( )【解析】选C.由奇函数的定义得y=sin x+sin2x是奇函数,排除选项B,又y=sin x+sin2x=sin x+sin xcos x=sin x(1+cos x),所以当x∈(0,π)时,函数y=sin x(1+cos x)>0,当x∈(π,2π)时,y=sin x(1+cos x)<0,排除选项D,又y′=cos x+cos2x,当x=π时,y′=0,所以函数在点(π,0)处的切线为x轴,排除选项A,故选C.7.已知A(2,1),B(6,x),C(10,0),D(3,8),若在上的投影为,则实数x的值为 ( )A.2B.-2C.4D.-4【解析】选C.依题意,=(4,x-1),=(7,-8),则在上的投影为===,解得x=4,故选C.8.△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,则= ( )A.+B.+C.+D.+【解析】选C.建立如图所示的直角坐标系,可得:C(0,0),A(0,3),B(4,0),由图知=λ,解得=λ+(1-λ)=(4-4λ,3λ),又⊥,=(4,-3),所以4×(4-4λ)+(-3)×3λ=0,λ=,所以=+.二、多项选择题(本题共4小题,每小题5分,共20分,多选题全部选对得5分,选对但不全对的得3分,有选错的得0分)9.已知集合A={0,1,2},B={a,2},若B⊆A,则a的值为( )A.0B.1C.2D.【解析】选AB.由B⊆A可知B={0,2}或B={1,2},所以a=0或1.10.定义在实数集R上的函数f(x)满足f(x)+f(x+2)=0,且f(4-x)=f(x).则以下说法正确的是( )A.函数f(x)的周期是4B.f(x)的图象关于直线x=2对称C.f(x)是偶函数D.f(x)是奇函数【解析】选ABC.由f(x)+f(x+2)=0得f(x+2)=-f(x),即f(x+4)=-f(x+2)=f(x),即f(x)的周期是4,又由f(4-x)=f(x)得f(x)的图象关于直线x=2对称;由f(4-x)=f(x)与f(x+4)=f(x)得f(4-x)=f(-x),f(-x)=f(x),即函数f(x)为偶函数.11.在△ABC中,内角A,B所对的边分别为a,b,若acos A=bcos B,则△ABC的形状是( )A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形【解析】选AB.由acos A=bcos B可得sin Acos A=sin Bcos B,即sin 2A=sin 2B,故2A=2B或2A+2B=π,故A=B或A+B=,即△ABC是等腰三角形或直角三角形.12.若x=1是函数f(x)=ax+ln x的极值点,则下列结论不正确的是( )A.f(x)有极大值-1B.f(x)有极小值-1C.f(x)有极大值0D.f(x)有极小值0【解析】选BCD.因为x=1是函数f(x)=ax+ln x的极值点,所以f′(1)=0,所以a+=0,所以a=-1,所以f(1)=-1,f′(x)=-1+=,当x>1时,f′(x)<0,当0<x<1时,f′(x)>0,因此f(x)有极大值-1. 三、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.已知函数f(x)=sin (ωx+φ)的图象过点,若f(x)≤f对x∈R恒成立,则ω的值为______;当ω最小时,函数g(x)=f-在区间[0,22]的零点个数为________. 【解析】由题意得φ=,且当x=时,函数f(x)取到最大值,故ω+=+2kπ,k∈Z,解得ω=1+12k,k∈N,又因为ω>0,所以ω的最小值为1,因此,g(x)=f-=sin x-在区间[0,22]上的零点个数是8个.答案:1+12k(k∈N) 814.(2019·菏泽模拟)如图,有5个全等的小正方形,=x+y,则x+y的值是________.【解析】因为=-,=2,=+=2-,所以=-=2-(2-)=3-2,又,不共线,=x+y,所以x+y=3-2,所以x=3,y=-2,x+y=1. 答案:115.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-log2x,则不等式f(x)<0的解集是______________. 世纪金榜导学号【解析】由题意得,f(x)<0等价于或即或解得x>2或-2<x<0,所以不等式的解集是(-2,0)∪(2,+∞).答案:(-2,0)∪(2,+∞)16.函数y=f(x)=x2e x在区间(a,a+1)上存在极值点,则实数a的取值范围为________.【解析】y′=2xe x+x2e x=xe x·(x+2),令y′=0,则x=0或-2,当-2<x<0时,f(x)在(-2,0)上单调递减,在(-∞,-2),(0,+∞)上单调递增,所以0或-2是函数的极值点.因为f(x)=x2e x在(a,a+1)上存在极值点,所以a<-2<a+1或a<0<a+1,所以-3<a<-2或-1<a<0.答案:(-3,-2)∪(-1,0)四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)(2020·石家庄模拟)已知二次函数f(x)的最小值为-4,且关于x的不等式f(x)≤0的解集为{x|-1≤x≤3,x∈R}.(1)求函数f(x)的解析式.(2)求函数g(x)=-4ln x的零点个数.【解析】(1)因为f(x)是二次函数,且关于x的不等式f(x)≤0的解集为{x|-1≤x≤3,x∈R},所以f(x)=a(x+1)(x-3)=ax2-2ax-3a,且a>0,f(x)min=f(1)=-4a=-4,a=1. 所以f(x)的解析式为f(x)=x2-2x-3.(2)因为g(x)=-4ln x=x--4ln x-2(x>0),所以g′(x)=1+-=.令g′(x)=0,得x1=1,x2=3.当x变化时,g′(x),g(x)的变化情况如表:x (0,1) 1 (1,3) 3 (3,+∞)g′(x) + 0 - 0 +g(x) ↗极大值↘极小值↗当0<x≤3时,g(x)≤g(1)=-4<0.又因为g(x)在(3,+∞)上单调递增,所以g(x)在(3,+∞)上只有1个零点.所以g(x)在(0,+∞)上只有1个零点.18.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,且ccos B+bcos C=2acos A.(1)求A;(2)若a=2,且△ABC的面积为,求△ABC的周长.【解析】(1)因为ccos B+bcos C=2acos A,所以sin Ccos B+sin Bcos C=2sin Acos A.所以sin(B+C)=2sin Acos A,sin A=2sin Acos A.因为A∈(0,π),所以sin A≠0,cos A=,所以A=.(2)因为△ABC的面积为,所以bcsin A=bc=,bc=4.由a=2,A=及a2=b2+c2-2bccos A,得4=b2+c2-4,所以b2+c2=8,又bc=4,所以b=c=2,所以△ABC的周长为6.19.(12分)(2019·大庆模拟)已知向量a=,b=(sin x,cos x),f(x)=a·b.(1)求f(x)的最大值及f(x)取最大值时x的取值集合M.(2)在△ABC中,a,b,c是角A,B,C的对边,若+∈M且c=1,求△ABC的周长的取值范围.【解析】(1)a=(cos x,-cos x),f(x)=a·b=sin xcos x-cos2x=sin 2x-cos 2x-=sin-,所以f(x)的最大值为1-,此时2x-=2kπ+,即x=kπ+,k∈Z,所以M=.(2)因为+∈M,所以+=kπ+,k∈Z,C=2kπ+,k∈Z,因为C∈(0,π),所以C=,因为c=1,由c2=b2+a2-2abcos C得c2=a2+b2-ab=(a+b)2-3ab≥(a+b)2-=,所以a+b≤2,又因为a+b>1,所以2<a+b+c≤3,即△ABC的周长的取值范围为(2,3].20.(12分)(2019·泰州模拟)已知函数f(x)=e x cos x-x. 世纪金榜导学号(1)求曲线y=f(x)在点(0,f(0))处的切线方程.(2)求函数f(x)在区间上的最大值和最小值.【解析】(1)因为f(x)=e x·cos x-x,所以f(0)=1,f′(x)=e x(cos x-sin x)-1,所以f′(0)=0,所以y=f(x)在(0,f(0))处的切线方程为y-1=0·(x-0),即y=1.(2)f′(x)=e x(cos x-sin x)-1,令g(x)=f′(x),则g′(x)=-2e x sin x≤0在上恒成立,且仅在x=0处等号成立,所以g(x)在上单调递减,所以g(x)≤g(0)=0,所以f′(x)≤0且仅在x=0处等号成立,所以f(x)在上单调递减,所以f(x)max=f(0)=1,f(x)min=f=-.21.(12分)已知函数f(x)=ln x-ax(a∈R).(1)当a=时,求f(x)的极值.(2)讨论函数f(x)在定义域内极值点的个数.【解析】(1)当a=时,f(x)=ln x-x,f(x)定义域为(0,+∞),f′(x)=-=,令f′(x)=0,得x=2,当x变化时,f′(x),f(x)的变化情况如表.x (0,2) 2 (2,+∞)f′(x) + 0 -f(x) ↗ln 2-1 ↘所以f(x)极大值为f(2)=ln 2-1,无极小值.(2)由(1)知,f(x)的定义域为(0,+∞),f′(x)=-a=(x>0).①当a≤0时,f′(x)>0在(0,+∞)上恒成立,即f(x)在(0,+∞)上单调递增,f(x)无极值点;②当a>0时,当x∈时,f′(x)>0,当x∈时,f′(x)<0,所以f(x)在x=处有极大值.综上,当a≤0时,f(x)无极值点,当a>0时,f(x)有一个极大值点x=.22.(12分)(2020·重庆模拟)已知函数f(x)=Asin(ωx+φ),其中A>0,ω>0,φ∈(0,π),x∈R,且f(x)的最小值为-2,f(x)的图象的相邻两条对称轴之间的距离为2π,f的图象关于原点对称. 世纪金榜导学号(1)求函数f(x)的解析式和单调递增区间.(2)在△ABC中,角A、B、C所对的边分别为a、b、c,且(4a2-2ac)cos B=a2+b2-c2,求f(B).【解析】(1)由已知,A=2,因为f(x)图象的相邻两条对称轴之间的距离为2π,所以T==4π,解得ω=,又因为f的图象关于原点对称,所以f(x)的图象关于对称,所以×+φ=kπ,k∈Z,解得φ=+kπ,k∈Z,又因为φ∈(0,π),所以φ=,所以f(x)=2sin.由-+2kπ≤x+≤+2kπ,k∈Z,得-+4kπ≤x≤+4kπ,k∈Z,所以f(x)的单调递增区间为,k∈Z.(2)在△ABC中,由已知及余弦定理得(4a2-2ac)=a2+b2-c2,即a2+c2-b2=ac,所以cos B=,又B∈(0,π),所以B=,f(B)=f=2sin=.关闭Word文档返回原板块快乐分享，知识无界！感谢您的下载!由Ruize收集整理！。

江苏省连云港市2021届新高考数学四模试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知双曲线222:1(0)3-=>y x C a a 的一个焦点与抛物线28x y =的焦点重合，则双曲线C 的离心率为（ ）A ．2B ．3C ．3D ．4 【答案】A【解析】【分析】根据题意，由抛物线的方程可得其焦点坐标，由此可得双曲线的焦点坐标，由双曲线的几何性质可得234a +=，解可得1a =，由离心率公式计算可得答案．【详解】根据题意，抛物线28x y =的焦点为(0,2)， 则双曲线22213y x a -=的焦点也为(0,2)，即2c =， 则有234a +=，解可得1a =，双曲线的离心率2c e a==. 故选：A ．【点睛】本题主要考查双曲线、抛物线的标准方程，关键是求出抛物线焦点的坐标，意在考查学生对这些知识的理解掌握水平．2．已知某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）A ．24πB ．28πC ．32πD ．36π【答案】C由三视图可知，几何体是一个三棱柱，三棱柱的底面是底边为23，高为1的等腰三角形，侧棱长为4，利用正弦定理求出底面三角形外接圆的半径，根据三棱柱的两底面中心连线的中点就是三棱柱的外接球的球心，求出球的半径，即可求解球的表面积.【详解】由三视图可知， 几何体是一个三棱柱，三棱柱的底面是底边为23，高为1的等腰三角形，侧棱长为4，如图：由底面边长可知，底面三角形的顶角为120o ， 由正弦定理可得2324sin120AD ==o ，解得2AD =， 三棱柱的两底面中心连线的中点就是三棱柱的外接球的球心，所以222222OA =+=该几何体外接球的表面积为：(24232S ππ=⋅=.故选：C 【点睛】 本题考查了多面体的内切球与外接球问题，由三视图求几何体的表面积，考查了学生的空间想象能力，属于基础题.3．已知点()11,A x y ，()22,B x y 是函数()2f x a x bx =的函数图像上的任意两点，且()y f x =在点1212,22x x x x f ⎛++⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭处的切线与直线AB 平行，则( ) A ．0a =，b 为任意非零实数 B ．0b =，a 为任意非零实数C ．a 、b 均为任意实数D ．不存在满足条件的实数a ，b 【答案】A【解析】【分析】求得()f x 的导函数，结合两点斜率公式和两直线平行的条件：斜率相等，化简可得0a =，b 为任意非依题意()'2f x bx =+，()y f x =在点1212,22x x x x f ⎛++⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭处的切线与直线AB平行，即有()1221b x x +=()1221a b x x x x =++-=，由于对任意12,x x 上式都成立，可得0a =，b 为非零实数.故选：A【点睛】本题考查导数的运用，求切线的斜率，考查两点的斜率公式，以及化简运算能力，属于中档题．4．在ABC V 中，D 为BC 边上的中点，且||1,|2,120AB AC BAC ==∠=︒u u u r u u u r ，则||=uuu r AD （）A B ．12 C ．34 D 【答案】A【解析】【分析】由D 为BC 边上的中点，表示出()12AD AB AC =+u u u r u u u r u u u r ，然后用向量模的计算公式求模. 【详解】解：D 为BC 边上的中点，()12AD AB AC =+u u u r u u u r u u u r ， ()12=2AD AB AC =+===u u u r u u u r u u u r故选：A【点睛】在三角形中，考查中点向量公式和向量模的求法，是基础题.5．根据最小二乘法由一组样本点(),i i x y （其中1,2,,300i =L ），求得的回归方程是ˆˆˆybx a =+，则下列说法正确的是( )A ．至少有一个样本点落在回归直线ˆˆˆybx a =+上 B ．若所有样本点都在回归直线ˆˆˆybx a =+上，则变量同的相关系数为1 C ．对所有的解释变量i x （1,2,,300i =L ），ˆˆibx a +的值一定与i y 有误差 D ．若回归直线ˆˆˆybx a =+的斜率ˆ0b >，则变量x 与y 正相关 【答案】D【解析】【分析】对每一个选项逐一分析判断得解.【详解】回归直线必过样本数据中心点，但样本点可能全部不在回归直线上﹐故A 错误；所有样本点都在回归直线ˆˆˆybx a =+上，则变量间的相关系数为1±，故B 错误； 若所有的样本点都在回归直线ˆˆˆy bx a =+上，则ˆˆbx a +的值与y i 相等，故C 错误；相关系数r 与ˆb符号相同，若回归直线ˆˆˆy bx a =+的斜率ˆ0b >，则0r >，样本点分布应从左到右是上升的，则变量x 与y 正相关，故D 正确．故选D ．【点睛】本题主要考查线性回归方程的性质，意在考查学生对该知识的理解掌握水平和分析推理能力.6．已知x,y 满足不等式组2202100x y x y x +-≤⎧⎪--≤⎨⎪≥⎩,则点(),P x y 所在区域的面积是( )A ．1B ．2C ．54D ．45【答案】C【解析】【分析】画出不等式表示的平面区域，计算面积即可.【详解】不等式表示的平面区域如图：直线220x y +-=的斜率为2-，直线21x y --的斜率为12，所以两直线垂直，故BCD ∆为直角三角形，易得(1,0)B ，1(0,)2D -，(0,2)C ，52BD =，5BC =所以阴影部分面积115552224BCD S BD BC ∆=⋅=⨯⨯=. 故选：C.【点睛】本题考查不等式组表示的平面区域面积的求法，考查数形结合思想和运算能力，属于常考题.7．某地区教育主管部门为了对该地区模拟考试成进行分析，随机抽取了200分到450分之间的2000名学生的成绩，并根据这2000名学生的成绩画出样本的频率分布直方图，如图所示，则成绩在[250，350]内的学生人数为（ ）A ．800B ．1000C ．1200D ．1600【答案】B【解析】【分析】由图可列方程算得a ，然后求出成绩在[250,350]内的频率，最后根据频数=总数×频率可以求得成绩在[250,350]内的学生人数.【详解】由频率和为1，得(0.0020.00420.002)501a +++⨯=，解得0.006a =，所以成绩在[250,350]内的频率(0.0040.006)500.5=+⨯=，所以成绩在[250,350]内的学生人数20000.51000=⨯=.故选：B【点睛】本题主要考查频率直方图的应用，属基础题.8．古希腊数学家毕达哥拉斯在公元前六世纪发现了第一、二个“完全数”6和28，进一步研究发现后续三个“完全数”分别为496，8128，33550336，现将这五个“完全数”随机分为两组，一组2个，另一组3个，则6和28恰好在同一组的概率为( )A ．15B ．25C ．35D ．110【答案】B【解析】【分析】推导出基本事件总数，6和28恰好在同一组包含的基本事件个数，由此能求出6和28恰好在同一组的概率．【详解】解：将五个“完全数”6，28，496，8128，33550336，随机分为两组，一组2个，另一组3个，基本事件总数2353C 10n C ==，6和28恰好在同一组包含的基本事件个数202123234m C C C C =+=，∴6和28恰好在同一组的概率42105m p n ===． 故选：B ．【点睛】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题． 9．执行如图所示的程序框图，输出的结果为（ ）A ．193B ．4C ．254D ．132【答案】A【解析】【分析】模拟执行程序框图，依次写出每次循环得到的,x M 的值，当3x =，1943M =>，退出循环，输出结果. 【详解】程序运行过程如下： 3x =，0M =；23x =，23M =；12x =-，16M =； 3x =，196M =；23x =，236M =； 12x =-，103M =；3x =，1943M =>，退出循环，输出结果为193， 故选：A.【点睛】该题考查的是有关程序框图的问题，涉及到的知识点有判断程序框图输出结果，属于基础题目. 10．某程序框图如图所示，若输出的120S =，则判断框内为（ ）A ．7?k >B ．6?k >C ．5?k >D ．4?k >【答案】C【解析】 程序在运行过程中各变量值变化如下表：K S 是否继续循环 循环前1 1 第一圈2 4 是 第二圈3 11 是 第三圈4 26 是 第四圈5 57 是 第五圈6 120 否故退出循环的条件应为k>5?本题选择C 选项.点睛：使用循环结构寻数时，要明确数字的结构特征，决定循环的终止条件与数的结构特征的关系及循环次数．尤其是统计数时，注意要统计的数的出现次数与循环次数的区别．11．已知函数3(1),1()ln ,1x x f x x x ⎧-≤=⎨>⎩，若()()f a f b >，则下列不等关系正确的是（ ）A ．221111a b <++BC ．2a ab <D ．()()22ln 1ln 1a b +>+ 【答案】B【解析】【分析】 利用函数的单调性得到,a b 的大小关系，再利用不等式的性质，即可得答案.【详解】∵()f x 在R 上单调递增，且()()f a f b >，∴a b >.∵,a b 的符号无法判断，故2a 与2b ，2a 与ab 的大小不确定，对A ，当1,1a b ==-时，221111a b =++，故A 错误； 对C ，当1,1a b ==-时，21,1a ab ==-，故C 错误；对D ，当1,1a b ==-时，()()22ln 1ln 1a b +=+，故D 错误；对B ，对a b >B 正确.故选：B.【点睛】本题考查分段函数的单调性、不等式性质的运用，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，属于基础题. 12．过双曲线22221x y a b-= (0,0)a b >>的左焦点F 作直线交双曲线的两天渐近线于A ,B 两点，若B 为线段FA 的中点，且OB FA ⊥（O 为坐标原点），则双曲线的离心率为（ ）AB C ．2 D 【答案】C【解析】 由题意可得双曲线的渐近线的方程为b y x a=±. ∵B 为线段FA 的中点，OB FA ⊥∴OA OF c ==，则AOF ∆为等腰三角形.∴BOF BOA ∠=∠由双曲线的的渐近线的性质可得BOF xOA ∠=∠∴60BOF BOA xOA ∠=∠=∠=︒ ∴tan 603b a =︒=，即223b a =. ∴双曲线的离心率为2222c a b a e aa a+==== 故选C. 点睛：本题考查了椭圆和双曲线的定义和性质，考查了离心率的求解，同时涉及到椭圆的定义和双曲线的定义及三角形的三边的关系应用，对于求解曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出,a c ，代入公式c e a=；②只需要根据一个条件得到关于,,a b c 的齐次式，转化为,a c 的齐次式，然后转化为关于e 的方程(不等式)，解方程(不等式)，即可得e (e 的取值范围)．二、填空题：本题共4小题，每小题5分，共20分。

江苏省淮安市2021届新高考数学四模考试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．定义：{}()()N f x g x ⊗表示不等式()()f x g x <的解集中的整数解之和.若2()|log |f x x =，2()(1)2g x a x =-+，{}()()6N f x g x ⊗=，则实数a 的取值范围是 A ．(,1]-∞- B ．2(log 32,0)-C ．2(2log 6,0]-D ．2log 32(,0]4- 【答案】D 【解析】 【分析】 【详解】由题意得，{}()()6N f x g x ⊗=表示不等式22|log |(1)2x a x <-+的解集中整数解之和为6.当0a >时，数形结合（如图）得22|log |(1)2x a x <-+的解集中的整数解有无数多个，22|log |(1)2x a x <-+解集中的整数解之和一定大于6.当0a =时，()2g x =，数形结合（如图），由()2f x <解得144x <<.在1(,4)4内有3个整数解，为1，2，3，满足{}()()6N f x g x ⊗=，所以0a =符合题意.当0a <时，作出函数2()|log |f x x =和2()(1)2g x a x =-+的图象，如图所示.若{}()()6N f x g x ⊗=，即22|log |(1)2x a x <-+的整数解只有1，2，3.只需满足(3)(3)(4)(4)f g f g <⎧⎨≥⎩，即2log 342292a a <+⎧⎨≥+⎩，解得2log 3204a -<≤，所以2log 3204a -<<. 综上，当{}()()6N f x g x ⊗=时，实数a 的取值范围是2log 32(,0]4-.故选D. 2．设函数()sin (0)5f x x πωω⎛⎫=+> ⎪⎝⎭，若()f x 在[0,2]π上有且仅有5个零点，则ω的取值范围为（ ） A ．1229,510⎡⎫⎪⎢⎣⎭B ．1229,510⎛⎤⎥⎝⎦ C ．1229,510⎛⎫⎪⎝⎭D ．1229,510⎡⎤⎢⎥⎣⎦【答案】A 【解析】 【分析】由02x π≤≤求出5x ωπ+范围，结合正弦函数的图象零点特征，建立ω不等量关系，即可求解. 【详解】当[0,2]x πÎ时，,2555x πππωπω⎡⎤+∈+⎢⎥⎣⎦， ∵()f x 在[]0,2π上有且仅有5个零点， ∴5265ππωππ≤+<，∴1229510ω≤<. 故选:A. 【点睛】本题考查正弦型函数的性质，整体代换是解题的关键，属于基础题.3．如图，在平面四边形ABCD 中，,,120,1,AB BC AD CD BAD AB AD ⊥⊥∠===o 若点E 为边CD 上的动点，则AE BE ⋅u u u v u u u v的最小值为 （ ）A ．2116B ．32C ．2516D ．3【答案】A 【解析】 【分析】【详解】分析：由题意可得ABD △为等腰三角形，BCD V 为等边三角形，把数量积AE BE ⋅u u u v u u u v分拆，设(01)DE tDC t =≤≤u u u v u u u v，数量积转化为关于t 的函数，用函数可求得最小值。

江苏省连云港市2021届新高考数学第四次押题试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若，则（ ）A ．B ．C ．D ．【答案】B 【解析】 【分析】由三角函数的诱导公式和倍角公式化简即可. 【详解】 因为，由诱导公式得，所以.故选B 【点睛】本题考查了三角函数的诱导公式和倍角公式，灵活掌握公式是关键，属于基础题. 2．,,a b αβαβ//////，则a 与b 位置关系是 ( ) A ．平行 B ．异面C ．相交D ．平行或异面或相交【答案】D 【解析】结合图(1)，(2)，(3)所示的情况，可得a 与b 的关系分别是平行、异面或相交．选D ．3．一只蚂蚁在边长为4的正三角形区域内随机爬行，则在离三个顶点距离都大于2的区域内的概率为( ) A ．316π-B ．34C ．36π D ．14【解析】 【分析】求出满足条件的正ABC ∆的面积，再求出满足条件的正ABC ∆内的点到顶点A 、B 、C 的距离均不小于2的图形的面积，然后代入几何概型的概率公式即可得到答案．【详解】满足条件的正ABC ∆如下图所示：其中正ABC ∆的面积为23443ABC S ∆== 满足到正ABC ∆的顶点A 、B 、C 的距离均不小于2的图形平面区域如图中阴影部分所示， 阴影部分区域的面积为21222S ππ=⨯⨯=. 则使取到的点到三个顶点A 、B 、C 的距离都大于2的概率是311643P π==-. 故选：A. 【点睛】本题考查几何概型概率公式、三角形的面积公式、扇形的面积公式的应用，考查计算能力，属于中等题．4．已知抛物线C ：28x y =，点P 为C 上一点，过点P 作PQ x ⊥轴于点Q ，又知点()5,2A ，则PQ PA+的最小值为（ ） A ．132B ．102C ．3D ．5【答案】C 【解析】 【分析】由2PQ PF =-,再运用,,P F A 三点共线时和最小，即可求解. 【详解】22523PQ PA PF PA FA +=-+≥-=-=.故选：C本题考查抛物线的定义，合理转化是本题的关键，注意抛物线的性质的灵活运用，属于中档题． 5．若不相等的非零实数x ，y ，z 成等差数列，且x ，y ，z 成等比数列，则x yz+=（ ） A ．52-B ．2-C ．2D ．72【答案】A 【解析】 【分析】 由题意，可得2x z y +=，2z xy =，消去y 得2220x xz z +-=,可得2x z =-，继而得到2z y =-，代入即得解 【详解】由x ，y ，z 成等差数列， 所以2x zy +=，又x ，z ，y 成等比数列， 所以2z xy =，消去y 得2220x xz z +-=，所以220x xz z⎛⎫+-= ⎪⎝⎭，解得1x z =或2x z =-，因为x ，y ，z 是不相等的非零实数，所以2x z =-，此时2zy =-， 所以15222x y z +=--=-． 故选：A 【点睛】本题考查了等差等比数列的综合应用，考查了学生概念理解，转化划归，数学运算的能力，属于中档题. 6．已知函数，其中04?,?04b c ≤≤≤≤，记函数满足条件：(2)12{(2)4f f ≤-≤为事件A ，则事件A 发生的概率为 A ．14B ．58C ．38D ．12【答案】D 【解析】 【分析】由(2)12{(2)4f f ≤-≤得4212424b c b c ++≤⎧⎨-+≤⎩，分别以,b c 为横纵坐标建立如图所示平面直角坐标系，由图可知，()12P A =.7．在平面直角坐标系xOy 中，将点()1,2A 绕原点O 逆时针旋转90︒到点B ，设直线OB 与x 轴正半轴所成的最小正角为α，则cos α等于( ) A ．25-B ．5-C ．5 D ．25-【答案】A 【解析】 【分析】设直线直线OA 与x 轴正半轴所成的最小正角为β，由任意角的三角函数的定义可以求得sin β的值，依题有OA OB ⊥,则90αβo=+，利用诱导公式即可得到答案.【详解】如图，设直线直线OA 与x 轴正半轴所成的最小正角为β因为点()1,2A 在角β的终边上，所以2225sin 512β==+依题有OA OB ⊥,则90αβo=+，本题考查三角函数的定义及诱导公式，属于基础题. 8．将函数()2sin(3)(0)f x x ϕϕπ=+<<图象向右平移8π个单位长度后，得到函数的图象关于直线3x π=对称，则函数()f x 在,88ππ⎡⎤-⎢⎥⎣⎦上的值域是（ ）A ．[1,2]-B ．[2]C ．⎡⎤⎢⎥⎣⎦D ．[2]【答案】D 【解析】 【分析】由题意利用函数sin()y A x ωϕ=+的图象变换规律，三角函数的图象的对称性，余弦函数的值域，求得结果. 【详解】解：把函数()2sin(3)(0)f x x ϕϕπ=+<<图象向右平移8π个单位长度后， 可得32sin 38y x πϕ⎛⎫=-+ ⎪⎝⎭的图象； 再根据得到函数的图象关于直线3x π=对称，33382k πππϕπ∴⨯-+=+，k Z ∈， 78πϕ∴=，函数7()2sin 38f x x π⎛⎫=+⎪⎝⎭.在,88ππ⎡⎤-⎢⎥⎣⎦上，753,824x πππ⎡⎤+∈⎢⎥⎣⎦，sin 382x π⎡⎤⎛⎫∴-∈-⎢⎥ ⎪⎝⎭⎣⎦，故()2sin 3[8f x x π⎛⎫=-∈ ⎪⎝⎭，即()f x 的值域是[2]，故选：D. 【点睛】本题主要考查函数sin()y A x ωϕ=+的图象变换规律，三角函数的图象的对称性，余弦函数的值域，属于中档题．9．若AB 为过椭圆22116925x y +=中心的弦，1F 为椭圆的焦点，则△1F AB 面积的最大值为（ ）【分析】先设A 点的坐标为(,)x y ，根据对称性可得(,)B x y --，在表示出1F AB ∆面积，由图象遏制，当点A 在椭圆的顶点时，此时1F AB ∆面积最大，再结合椭圆的标准方程，即可求解. 【详解】由题意，设A 点的坐标为(,)x y ，根据对称性可得(,)B x y --， 则1F AB ∆的面积为122S OF y c y =⨯⨯=， 当y 最大时，1F AB ∆的面积最大，由图象可知，当点A 在椭圆的上下顶点时，此时1F AB ∆的面积最大，又由22116925x y +=，可得椭圆的上下顶点坐标为(0,5),(0,5)-，所以1F AB ∆的面积的最大值为16925560S cb ==-⨯=. 故选：D.【点睛】本题主要考查了椭圆的标准方程及简单的几何性质，以及三角形面积公式的应用，着重考查了数形结合思想，以及化归与转化思想的应用.10．某几何体的三视图如图所示，则此几何体的体积为（ ）A．23B．1 C．43D．83【答案】C【解析】该几何体为三棱锥，其直观图如图所示，体积114222323V⎛⎫=⨯⨯⨯⨯=⎪⎝⎭．故选C.11．各项都是正数的等比数列{}n a的公比1q≠，且2311,,2a a a成等差数列，则3445a aa a++的值为()A15-B51+C51-D51+51-【答案】C【解析】分析：解决该题的关键是求得等比数列的公比，利用题中所给的条件，建立项之间的关系，从而得到公比q所满足的等量关系式，解方程即可得结果.详解：根据题意有213122a a a+=⋅，即210q q--=，因为数列各项都是正数，所以15q+= 34151a a+-===，故选C.点睛：该题应用题的条件可以求得等比数列的公比q ，而待求量就是1q，代入即可得结果. 12．双曲线()221x y m c m-=>的一条渐近线方程为20x y +=，那么它的离心率为（ ）A B ．C D 【答案】D 【解析】 【分析】根据双曲线()221x y m c m-=>的一条渐近线方程为20x y +=，列出方程，求出m 的值即可.【详解】∵双曲线()221x y m c m-=>的一条渐近线方程为20x y +=，12=，∴4m =，∴双曲线的离心率c e a ==. 故选：D. 【点睛】本小题主要考查双曲线离心率的求法，属于基础题. 二、填空题：本题共4小题，每小题5分，共20分。