精心整理的运筹学重点11.决策论
- 格式:pdf
- 大小:181.86 KB
- 文档页数:6


何谓决策论?决策论详述决策论(DecisionTheory)是根据信息和评价准则,用数量方法寻找或选取最优决策方案的科学,是运筹学的一个分支和决策分析的理论基础。
在实际生活与生产中对同一个问题所面临的几种自然情况或状态,又有几种可选方案,就构成一个决策,而决策者为对付这些情况所取的对策方案就组成决策方案或策略。
中文名:决策论含义:选取最优决策方案外文名:Decision Theory时间:1815年1、决策论:决策论是在概率论的基础上发展起来的。
随着概率论的发展,早在1763年贝叶斯发表贝叶斯定理时起,统计判定理论就已发萌芽。
1815年拉普拉斯用此定理估计第二天太阳还将升起的概率,把统计判定理论推向一个新阶段。
统计判定理论实际上是在风险情况下的决策理论。
这些理论和对策理论概念上的结合发展成为现代的决策论。
决策论在包括安全生产在内的许多领域都有着重要应用。
2、决策问题的分类:决策问题根据不同性质通常可以分为确定型、风险型(又称统计型或随机型)和不确定型三种。
确定型决策:是研究环境条件为确定情况下的决策。
如某工厂每种产品的销售量已知,研究生产哪几种产品获利最大,它的结果是确定的。
确定型决策问题通常存在着一个确定的自然状态和决策者希望达到的一个确定目标(收益较大或损失较小),以及可供决策者选择的多个行动方案,并且不同的决策方案可计算出确定的收益值。
这种问题可以用数学规划,包括线性规划、非线性规划、动态规划等方法求得最优解。
但许多决策问题不一定追求最优解,只要能达到满意解即可。
风险型决策:是研究环境条件不确定,但以某种概率出现的决策。
风险型决策问题通常存在着多个可以用概率事先估算出来的自然状态,及决策者的一个确定目标和多个行动方案,并且可以计算出这些方案在不同状态下的收益值。
决策准则有期望收益最大准则和期望机会损失最小准则。
风险情况下的决策方法通常有最大可能法,损益矩阵法和决策树法三种。
最大可能法是在一组自然状态中当某个状态出现的概率比其他状态的大得多,而它们相应的益损值差别又较小的情况下所采用的一种方法。

1.科学决策科学决策是指决策者凭借科学思维,利用科学手段和科学技术所进行的决策。
程序性:在正确的理论指导下,按照一定的程序,正确运用决策技术和方法来选择行为方案。
创造性:决策总是针对需要解决的问题和需要完成的新任务,运用多种思维方法进行的创造性劳动。
择优性:在多个方案的对比中寻求能获取较大效益的行动方案,择优是决策的核心。
指导性:决策结果必须指导实践。
2. 运筹学运筹学是一种科学决策方法。
是依据给定目标和条件从众多方案中选择最优方案的最优化技术。
是一门寻求在给定资源条件下,如何设计和运行一个系统的科学决策方法。
与管理科学关系:管理科学涵盖的领域比运筹学更宽一些。
可以说,运筹学是管理科学最重要的组成部分。
与系统科学、系统分析、工业工程的关系:系统科学、系统分析、工业工程等学科的研究内容比运筹学的研究内容窄一些。
3.运筹学研究的特点科学性:运筹学是在科学方法论的指导下通过一系列规范化步骤进行的;运筹学是广泛利用多种学科的科学技术知识进行的研究。
运筹学研究不仅仅涉及数学,还要涉及经济科学、系统科学、工程物理科学等其它学科。
实践性:运筹学以实际问题为分析对象,通过鉴别问题的性质、系统的目标以及系统内主要变量之间的关系,利用数学方法达到对系统进行最优化的目的。
分析获得的结果要能被实践检验,并被用来指导实际系统的运行。
系统性:运筹学用系统的观点来分析一个组织(或系统),它着眼于整个系统而不是一个局部,通过协调各组成部分之间的关系和利害冲突,使整个系统达到最优状态。
综合性:运筹学研究是一种综合性的研究,它涉及问题的方方面面,应用多学科的知识,因此,要由一个各方面的专家组成的小组来完成。
4.运筹学模型运筹学研究的模型主要是抽象模型:数学模型。
数学模型的基本特点是用一些数学关系(数学方程、逻辑关系等)来描述被研究对象的实际关系(技术关系、物理定律、外部环境等)。
4.1模型特点它们大部分为最优化模型。
一般来说,运筹学模型都有一个目标函数和一系列的约束条件,模型的目标是在满足约束条件的前提下使目标函数最大化或最小化。

运筹学中的优化理论和决策分析运筹学是一种科学理论和方法论,主要研究如何制定最优决策,以实现效益最大化。
它主要通过数学模型和计算机仿真等手段,对复杂系统进行优化分析和决策支持,以达到最优化的结果。
优化理论作为运筹学的核心竞争力,是运用数学、工程等学科的方法来解决最优化问题的理论体系,旨在实现最佳决策的目的。
本文将围绕运筹学中的优化理论和决策分析展开讨论。
一、优化理论优化理论是指通过数学分析和计算机仿真等手段,对具有一定复杂性的系统进行分析,从而实现最优化的结果。
优化问题是指在一定的限制条件下,寻求某种指标或目标函数的最优值。
如何处理约束条件和目标函数之间的相互制约关系,是优化问题研究中的核心难题。
因此,优化理论主要通过建立数学模型和算法设计等手段,实现最优决策的目标。
1. 建立数学模型建立数学模型是优化理论的核心。
数学模型通常包括决策变量、目标函数、约束条件等要素。
决策变量是指决策者的选择变量,而目标函数则是指要优化的指标或目标。
约束条件则是指决策制定过程中需要考虑的各类限制因素。
通过将系统建模,可以得到系统的优化方案,并为制定最优决策提供途径。
2. 算法设计算法设计是实现最优化的核心。
常见的算法包括线性规划、非线性规划、动态规划、整数规划等。
不同种类的算法在面对不同的优化问题时,具有各自的优缺点。
因此,在实际应用中,需要根据优化问题特征选择相应的算法进行求解。
3. 求解方法求解方法是指实现算法的具体操作过程,包括求解器、迭代算法、搜索算法等。
求解方法的选择与算法种类密切相关。
通过对数学模型建立算法,并运用求解方法进行求解,可以在有限的时间内得到最优化结果。
二、决策分析决策分析是指对决策问题进行全面、系统地分析,从而为制定最优决策提供支持。
决策分析主要涵盖了决策建模、风险分析、方案评估和数据挖掘四个方面。
1. 决策建模决策建模是指对问题进行抽象、形式化的过程,将现实问题映射到数学模型中进行分析和求解。



判断题判断正误,如果错误请更正第十一章决策论1.在不确定型决策中,最小机会损失原则比等可能性则保守性更强。
2.决策树比决策矩阵更适于描述序列决策过程。
3.在折衷主义原则中,乐观系数α的确定与决策者对风险的偏好有关。
选择题在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。
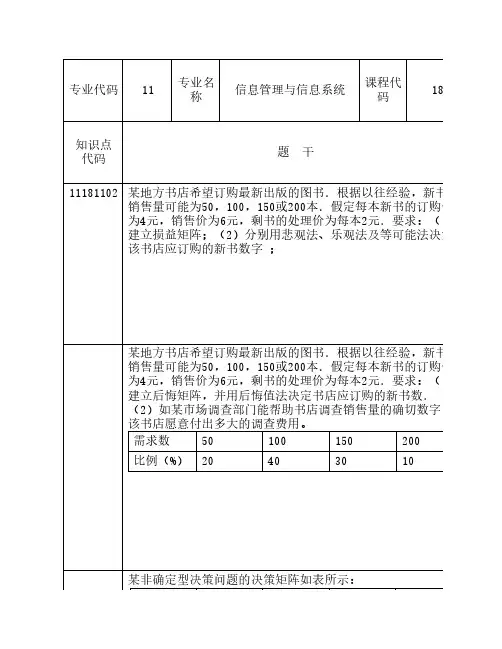
第11章决策论1.对于不确定型的决策有主观者的态度不同基本可分为以下几种准则A 乐观主义准则 B 悲观主义准则 C 最大期望收益准则 D 等可能性准则 E 最小机会损失准则2.对于不确定型的决策,某人采用乐观注意准则进行决策,则应在收益表中 A 大中取大 B 大中取小C 小中取大D 小中取小3.下列哪项不属于按环境分类的决策 A 确定型 B 不确定型 C 风险型 D单项决策型4.下列哪项是面向决策结果的方法的程序 A 收集信息→确定目标→提出方案→方案优化→决策 B确定目标→收集信息→决策→提出方案→方案优化 C B确定目标→收集信息→提出方案→方案优化→决策 D确定目标→提出方案→收集信息→方案优化→决策5.按决策过程过程的连续性应将决策分为哪几类 A 暂时决策 B 序贯决策 C长期决策 D 单项决策 E 程序化决策计算题11.1某地方书店希望订购最新出版的图书.根据以往经验,新书的销售量可能为50,100,150或200本.假定每本新书的订购价为4元,销售价为6元,剩书的处理价为每本2元.要求:(1)建立损益矩阵;(2)分别用悲观法、乐观法及等可能法决策该书店应订购的新书数字;(3)建立后悔矩阵,并用后悔值法决定书店应订购的新书数.(4)书店据以往统计资料新书销售量的规律见表11-13,分别用期望值法和后悔值法决定订购数量;(5)如某市场调查部门能帮助书店调查销售量的确切数字,该书店愿意付出多大的调查费用。
表11-13(21423(3)后悔矩阵如表11.1-2所示。
23(4)按期望值法和后悔值法决策,书店订购新书的数量都是100本。



运筹学复习要点第二章线性规划与单纯形法一、标准型:规定具有下述条件的线性规划问题为标准型式的线性规划问题:1、目标函数为求最大;2、约束条件为等式约束;3、决策变量为非负。
二、线性规划问题具有的特征:1、每一问题都用一组决策变量(x1, x2, . . . ,xn)表示某一方案;2这组决策变量的值就代表一个具体方案,一般这些变量值是非负的;3、存在一定的约束条件,它们可用线性等式或不等式表示;4、都有一个要求达到的目标,它们可用决策变量的线性函数表示,称目标函数。
根据问题不同,要求目标函数实现最大化或最小化。
三、图解法的结论:1、可行域一定是凸集,即该区域内任意两点间连线上的点仍在该区域内;2、线性规划最优解不可能在凸集内的点上实现;3、线性规划问题有可能存在无穷多最优解;4、如果可行域无界,则最优解可能是无界解;5、如果不存在可行域,则没有可行解,也一定不存在最优解;6图解法只适用于两个决策变量的情况。
四、单纯形法:其基本思路是首先确定一个初始基可行解,然后判断该基可行解是否为最优解。
如果是最优解,则求解过程结束;如果不是最优解,则在此基础上变换找出另一个基可行解,该基可行解的目标函数值应该优于原基可行解。
再判断新的基可行解是否为最优解,如果是最优解,则求解过程结束;如果不是最优解,则在此基础上变换再找出另一个新基可行解,如此进行下去,直到找到最优解为止。
五、最优性检验与解的形式:最优解的判别定理,若X(0) = (b′1, b′2, ……… ,b′m, 0, …… , 0)T为对应于基B的一个基可行解,且对于一切j = m + 1, …… , n,有σj6 0,则X(0)为最优解,称σj为检验数。
无穷最多解判别定理,若X(0) = (b′1, b′2, …… , b′m, 0, …… , 0)T为对应于基B的一个基可行解,且对于一切j = m + 1, …… , n,有σj6 0,又存在某个非基变量的检验数σm+k= 0,则线性规划问题有无穷多最优解。
第十一章 决策论 1.决策过程:1)确定目标;2)建立可行方案;3)方案的评价和选择;4)方案实施 由于决策信息不足,决策者无法知道各自然状态发生的任何信息,因此决策的结果往往取决于决策者的主观态度。
不同的心理、不同的冒险精神的人可以选用不同的方法。
1)乐观法决策(最大最大准则):从每个策略行取最大值,再从列中再取最大。
Max---max策略。
2)悲观法决策(华尔德准则,最大最小准则):从每个策略行取最小值,再从列中再取最大。
Min---max策略。
3)折中法决策(郝威茨准则,乐观系数法):用折中系数α算出每个策略的折中值,再选最大的。
max策略 max min max{|(1)}i i ij ij h h a a αα=+− 4)等可能性决策(拉普拉斯准则):以全部状态的期望损益值作为决策依据,比折中法更好。
缺点是认为各种状态的概率相等,不大现实。
12111max{...}j j mj j j ja a a n n n +++∑∑∑ 5)最小后悔值法:后悔值矩阵中采用Max---min策略 从每个状态(列)找出最大值;用这个最大值减去该列每个策略的效益值,得到后悔值表;在后悔值表中选择每一行中的最大值加入右列;从所有最大后悔值中选择最小的。
3.风险型决策 1)最大期望收益准则:根据各事件发生的概率,计算每一个策略的期望收益值,并从中选择最大的期望收益值。
2)最小期望损失准则(后悔值):首先构造后悔值矩阵,然后分别计算不同策略的期望机会损失,从中选择最小的一个。
3)全情报价值EVPI(Expected value of perfect information):计算出如果获得这项情报而使决策者的期望收益提高的数额,这个数额称为完全情报的期望值,如果它大于采集情报所花的费用,则采集这一情报是有价值的,否则就得不偿失,因此把EVPI作为采集情报费用的上限。
2)按最大期望收益准则公司应该选择方案1a ,期望收益为32万元。
3)假定情报指出销路好,公司就选取2a 策略,可获利75万,假定情况指出销路一般,公司就选取1a 策略,可获利40万,假定情报是销路差,公司选择3a 策略,获利0万。
由于在获取全情报之前无法确切知道情报内容,故只能算出期望收益0.3*75+0.5*40+0.2*0=42.5万。
4)可知全情报会使期望收益增加,即EVPI=42.5-32=10.5万。
5)只要获得全情报的花费不超过10.5万,就值得去获取全情报。
4)贝叶斯决策 全概率公式:1()()(|)ni i i P B P A P B A ==∑ 贝叶斯公式:1()()(|)(|)()()(|)k k k k n i i i P A B P A P B A P A B P B P A P B A ===∑ 1、已知类条件概率密度参数表达式和先验概率。
2、利用贝叶斯公式转换成后验概率。
3、根据后验概率大小进行决策分类。
例:公司委托某市场机构进行相关市场调查。
为了了解该机构的可靠性,对其以往的调查记录进行分析,得到有关数据表如下,表中数据的意义是:当实际结果为销路好时,调查结果也是销路好的条件概率为'11(|)0.7P s s =,调查结果是销路一般的条件概率为'21(|)0.2P s s =,调查结果为销路差的条件概率为'31(|)0.1P s s =。
其余类推。
进行市场首先计算出各种调查结果出现的概率 ''''1111212313()()(|)()(|)()(|)0.3*0.70.5*0.150.2*0.10.305P s P s P s s P s P s s P s P s s =++=++= ''''2121222323()()(|)()(|)()(|)0.3*0.20.5*0.700.2*0.20.45P s P s P s s P s P s s P s P s s =++=++= ''''2131232333()()(|)()(|)()(|)0.3*0.10.5*0.150.2*0.70.245P s P s P s s P s P s s P s P s s =++=++= 由贝叶斯公式1()()(|)(|)()()(|)k k k k n i i i P A B P A P B A P A B P B P A P B A ===∑计算出后验概率'(|)j i P s s '(|)j iP s s 销路好'1s (0.3) 销路一般'2s (0.5) 销路差'3s (0.2) 销路好1s 0.689 0.133 0.122 销路一般2s 0.246 0.778 0.306 销路差3s 0.065 0.089 0.572 表:市场调查后的后验概率表 123()0.689*600.246*400.065*(30)49.23()0.689*750.246*350.065*(50)57.035()0.689*500.246*200.065*039.37E a E a E a =++−==++−==++= 应选择2a 如果市场调查的结果是销路一般,各方案的期望值为: 123()0.133*600.778*400.089*(30)36.43()0.133*750.778*350.089*(50)32.755()0.133*500.778*200.089*022.21E a E a E a =++−==++−==++= 应选择1a 如果市场调查的结果是销路差,各方案的期望值为: 123()0.122*600.306*400.572*(30) 2.40()0.122*750.306*350.572*(50)8.74()0.122*500.306*200.572*012.22E a E a E a =++−==++−=−=++= 应选择3a 根据后验概率进行决策的期望利润为: 0.305*57.035+0.45*36.43+0.345*12.22=36.783万元 仅根据先验信息进行决策时的期望利润为32万,进行市场调查科增加期望利润,也就是市场调查所获得的补充信息的价值为36.783-32=4.783万元,大于进行市场调查的费用,因而委托调查机构进行市场调查是合算的. 1211122122*122221121122(1)(1)()()a p a p a p a p a a p a a a a +−=+−−=+−+当*p p =两方案无差异,*p p >方案1s 优于2s 即12s s >,当*p p <,方案2s 优于1s ,即21s s <(灵敏度分析) 5.马尔科夫决策 例3 某地区有甲、乙、丙三家公司,过去的历史资料表明,这三家公司某产品的市场占有率分别为50%,30%和20% 。
不久前,丙公司制定了一项把甲、乙两公司的顾客吸引到本公司来的销售和服务措施。
设三家公司的销售和服务是以季度为单位考虑的。
市场调查表明,在丙公司新的经营方针的影响下,顾客的转移概率矩阵为: 使用马尔科夫分析方法研究此销售问题,并分别求出三家公司在第一、二季度各拥有的市场占有率和最终的市场占有率。
解:设随机变量Xt=1,2,3(t =1,2,3)分别表示顾客在t季度购买甲、乙和丙公司的产品,显然{Xt}是一个有限状态的马尔科夫链。
已知P(X0=1)=0.5, P(X0=2)=0.3, P(X0=3)=0.2,又已知马尔科夫链的一步转移概率矩阵,于是第一季度的销售份额为 即第一季度甲、乙、丙三公司占有市场的销售份额分别为39%,30%和31%。
再求第二季度的销售份额,有 即第二季度三家公司占有市场的销售份额分别为31.9%,29.4%和38.7%。
设π1 ,π2 ,π3为马尔科夫链处于状态1,2,3的稳态概率,由于P是一个标准概率矩阵,因此有 解得π =( π1 ,π2 ,π3 )=(0.1765,0.2353,0.5882)故甲、乙、丙三家公司最终将分别占有18%,23%和59%的市场销售份额。
定理:设P是标准概率矩阵,则必存在非零向量π = (π1 ,π2 , ・・・, πn)使得π P= π,称π为P的平衡向量。
如果进一步满足:π1+ π2+ ・・・+ πn=1 称此πj为状态sj 的稳态(平衡)概率。
P的这一特性在实用中有重要的价值。
通常在市场预测中,所讨论的用户转移概率矩阵就属于标准概率矩阵,它可以通过几步转移达到稳定(平衡)状态。
在这种情况下,各厂家的用户占有率不再发生变化,此时的π称为最终用户的占有率P向量。
例4 考虑例3的销售问题。
为了对付下降的销售趋势,甲公司考虑两种对付的策略: 第一种策略是保留策略,即力图保留原有顾客的较大百分比,并对连续两期购货的顾客给予优惠价格,可使其保留率提高到85%,新的转移概率矩阵为 第二种策略是争取策略,即甲公司通过广告宣传或跟踪服务来争取另外两家公司的顾客,新的转移概率矩阵为 试问: (1)分别求出在甲公司的保留策略和争取策略下,三家公司最终分别占有市场的份额;(2)若实际这两种策略的代价相当,甲公司应采取哪一种策略? 解: (1)在保留策略下,有 解得π = (π1 ,π2 ,π3 ) = (0.316, 0.263, 0.421),即在保留策略下,三家公司最终将各占31.6%, 26.3%和42.1%的市场份额。
同理可以求得在争取策略下的市场占有份额,三家公司最终将各占33.3%, 22.2%和44.5%的市场份额。
(2)在保留策略下甲公司将占31.6%的市场份额,而在争取策略下将占33.3%的市场份额,故甲公司应采取争取策略。
。