薄膜干涉等厚条纹共25页

λ 明环： δ = 2e + = kλ r 2 e= 代入 2R λ λ 暗环：δ = 2e + = ( 2k + 1) 2 2 得 o · ( 2 k − 1) R λ R 明环半径： rk = λ 2 r 平凸透镜 e r = kR λ 暗环半径： k 平晶 条纹特点： (1) rk与环的级次的平方根成正比； (2)中心为0级暗斑，越往外级次越高； (3) 越向外环越密，即内疏外密。
肥皂膜显示的明亮颜色， 火玛瑙： 是什么原因造成的呢？ 为什么会闪出火红色的晕 答案在本次讲课中。 彩，而称其为火玛瑙呢？
中国石油大学，冯金波
第3章
光的干涉
§3.2 相干光 §3.1 杨氏双缝干涉 §3.5 光程 §3.6 薄膜干涉（一）——等厚干涉 §3.7 薄膜干涉（二）——等倾干涉 §3.8 迈克尔孙干涉仪 §3.3 光的非单色性对干涉条纹的影响 §3.4 光源的大小对干涉条纹的影响
∆e 条纹间距：L = sin θ
λ L= 2 n sin θ λ ≈ 2 nθ
�等厚干涉条纹
劈尖
不规则表面
中国石油大学，冯金波
引子：五彩缤纷的肥皂膜（答案）
δ (e ) = kλ , k = 1,2 ,3 ,… 干涉相长 λ δ (e ) = ( 2k + 1) , k = 0 ,1,2 ,… 2 干涉相消 λ δ (e ) = 2ne + 2
f
λ n + ′ − δ = ( AB + BC ) n AD 2 e AB = BC = cos r
S
i
n′ n > n′ n′
·
i
1
i
2
i
A
· ·ri · ·

3
利用光具组将同一列波分解，使它们经过不同的途径后重 新相遇，由于这样的两列波由同一列波分解而来，它们频 率相同，位相差稳定，振动方向也可做到基本平行，因而 满足相干条件，能产生干涉图样。实际的干涉装置按分解 波列的方法不同分为两种： i）分波前法将点光源的波前分割为两部分的波列分解法称 为分波前法，杨氏双缝是分波前法的典型代表 ii）分振幅法利用两种媒质的界面将振幅分解为反射和透 射两部分的波列分解法称为分振幅法。分振幅法的典型代 表是薄膜干涉和迈克尔逊干涉仪。
膜厚增大，条纹细锐 中心条纹没有周围细锐
28
2.观察等倾条纹时扩展光源的作用
29
3.薄膜干涉的定域问题
30
31
32
33
i) 条纹偏离等厚线：
14
ii) 反衬度下降：
15
6. 薄膜的颜色、增透膜和高反膜
16
增透膜
17
18
高反膜
（1） （2） （3） （4） （5） （6） （1） （2） （3） （4） （5） （6） H L H L H L H
基底
19
20
降低反射率
黑硅
21
作业：P300， 2, 3, 5, 6
8
2.薄膜表面的等厚条纹（i固定h变化）
光程差计算：
9
10
3.楔形薄膜的等厚干涉
11
12
4.牛顿圈（环）
13
5.等厚干涉条纹的观测方法及倾角的影响
严格的等厚干涉要求点光源、正入射。但扩展光源、斜入射，用眼睛 也能观察到干涉现象。主要是眼睛的瞳孔对光束进行了限制，只是干 涉的结果会受到一定的影响。
中心处条纹较稀疏。
膜厚增大，条纹变密。
27

n
h
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2.6 薄膜的颜色、增透膜和高反膜 薄膜的颜色：干涉导致不同波长光的反射率不同。 增透膜：
n1 < n < n 2 nh = λ 4 , n1 n n2
例： n1 = 1,
3λ 4 ,
n1 n 2 时完全消光
→ n 0 = 1 . 23
2.2 薄膜表面的等厚条纹（i固定，h变化） 光程差计算：
Q
i1
C
n
A
i
B
P
h
Δ L ( P ) = ( QABP ) − ( QP ) = ( QA ) − ( QP ) + ( ABP ) Δ L ( P ) ≈ 2 nh cos i
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2 nh cos i = conL ) = − 2 nh sin i δ i + 2 n cos i δ h = 0
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2.5 等厚干涉条纹的观测方法及倾角的影响 ii)反衬度下降： 眼睛瞳孔限制扩展光源 参与干涉的区域。光源 不同处的 i 不同， h 越 大，反衬度越低。
rk2+ m − rk2 R= mλ
由于半波损失，中心时暗纹。
rk
DP k2 = CP k2 − CD 2 rk2 = R 2 − ( R − h k ) 2 = 2 Rh k − h k2
第三章：干涉装置 光场的时空相干性 § 2 薄膜干涉（一）——等厚条纹
2.5 等厚干涉条纹的观测方法及倾角的影响 严格的等厚干涉要求点光源、正入射。但扩展光源、斜入 射，用眼睛也能观察到干涉现象。主要是眼睛的瞳孔对光 束进行了限制，只是干涉的结果会受到一定的影响。 i) 条纹偏离等厚线： 干涉条纹：

六、迈克耳孙干涉仪
M2 M1
2
G1 S G2 1 1
光束2′和1′发生干涉
M1
若M1、M2平行 等倾条纹 若M1、M2有小夹角 等厚条纹
半透半 反膜 2
若条纹为等厚条纹， M1 平移d 时，干涉条移过N 条，则有：
应用： •微小位移测量 •测折射率
d N
2
D

L
ek 1 ek b sin 2n2 sin 2n2
D L
在入射单色光一定时，劈尖的楔角愈小，则b 愈大， 干涉条纹愈疏； 愈大，则b 愈小，干涉条纹愈密。 当用白光照射时，将看到由劈尖边缘逐渐分开的
彩色直条纹。
3.劈尖干涉的应用：
干涉膨胀仪：利用空气劈尖干涉原理测定样品 的热膨胀系数 平板 玻璃
k 1,2,3 明条纹
r kR
k 0,1,2 暗条纹
r
( 2k 1) R 2
k 1,2,3 明条纹
r kR
k 0,1,2 暗条纹

•随着牛顿环半径的增大，条纹变得 越来越密。 • e=0,两反射光的光程差 =/2，为 暗斑。
标准 待测
暗 纹
• 检验透镜球表面质量
17-4 等倾干涉 等厚干 涉 利用薄膜上、下两个表面对入射光的反射和折
射，可在反射方向（ 或透射方向）获得相干光束。 分振幅法
一、薄膜干涉 扩展光源照射下的薄膜干涉
在一均匀透明介质n1中 放入上下表面平行,厚度
n1 为e 的均匀介质 n2(>n1)， n A 2 用扩展光源照射薄膜，其 n1
反射和透射光如图所示
实心劈尖：n1=1,垂直入射i=0
干涉条件
对空气劈尖：n2=1

加热时，待测 材料膨胀，上表 面上升，条纹有 什么变化？
待测材料膨胀后，空气膜变薄，条纹向远离劈棱 的方向移动。 每移动一个条纹，空气膜厚度变化为：h=/2 移过m条，则说明膨胀: h=m(/2)
next next
2
13
14
白光入射薄膜时，条纹如何分布？ 白光照射下的肥皂膜
例：检查光学平面的平整度 标准平面 空气 待测平面
next
3、光程差
/ 2 2hn 2 cos i 2 0 0
3
二、劈尖干涉 劈尖：上下表面都是平面的透明体，两表面之间有 一个很小的夹角。 1. 条纹形状

4
上、下表面夹角很小时，在局部可近似认为是平行膜：
0和i2固定，只与h 有关， 同一级条纹出现 在薄膜厚度相同处，故称 等厚条纹。 条纹的特点由薄膜厚h度变化的规律决定。
n2 2n2
21
22
r1 : r2 : r3 : ...... 1 : 2 : 3 : ...... 无额位光程差时， r1 : r2 : r3 : ...... 1 : 3 : 5 : ...... 有额位光程差时，
条纹内疏外密，级次内低外高 透镜上移时: 条纹收缩，中心条纹被吞没。 透镜下移时: 条纹扩展，中心有条纹冒出。 球面半径变化时，条纹如何变化？
25
两个力在竖直方向平衡： d·Fn·cos= g·dm 水平方向满足：d·Fn·sin=2r·dm tan = 2r/g
tan dy dr
26
水旋转时表面为旋转对称曲面，取过水面最低点的 竖直线为y轴，原点o在水盘底面。 取水表面上某一点P处质量为dm的水元。

y
1 2 2 r C 表示水膜的厚度 2 g

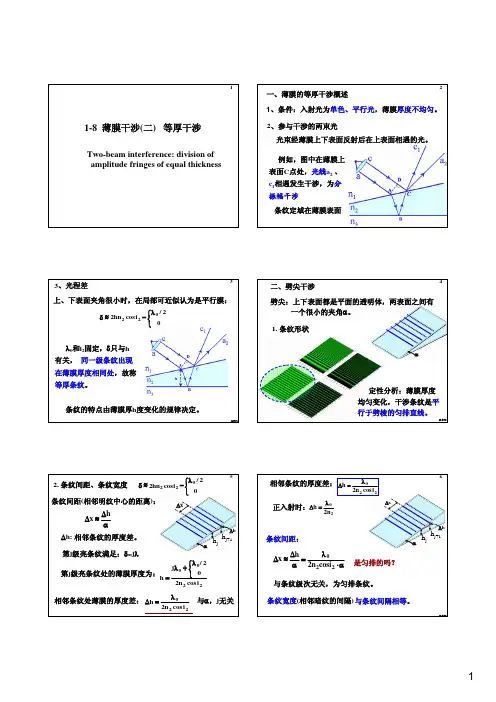
一、薄膜的等厚干涉概述1、条件：入射光为单色、平行光，薄膜各处厚度不同。

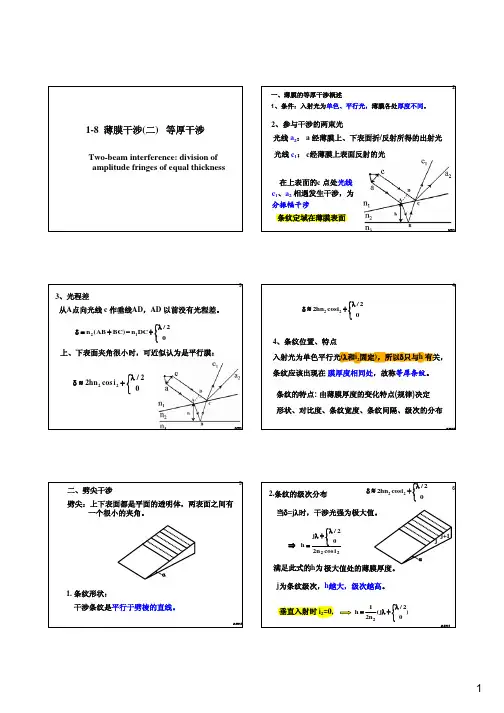
光线c 1：c 经薄膜上表面反射的光2、参与干涉的两束光光线a 2：a 经薄膜上、下表面折/反射所得的出射光在上表面的c 点处光线c 1、a 2相遇发生干涉，为分振幅干涉条纹定域在薄膜表面next2⎩⎨⎧λ+−+=δ02/DC n )BC AB (n 1222/22hn cos i 0λ⎧δ≈+⎨⎩3、光程差从A 点向光线c 作垂线AD ，AD 以前没有光程差。

上、下表面夹角很小时，可近似认为是平行膜：next3红线对应膜厚相同的位置。

劈角由小变大时，条纹由疏变密，反之亦然i＝0，∆h≈λ/2。

2处为暗条纹。

2、测量微小变化例：干涉膨胀仪平玻璃与被测材料表面之间形成空气劈尖，光垂直照射，看反射光的干涉条纹。

加热，被测材料膨胀，表面上升，条纹有什么变化？next19待测材料膨胀后，空气膜变薄，如图所示，虚线纹局部弯曲，变为：若条纹的最大变形线度为单色平行光垂直入射为圆心的圆，所以条纹是以O 点条纹位置由圆条纹半径决定。

2/⎧λ25条纹向中间收缩，中心条纹被吞没。

10.5mm ，则水的旋转角速度为多少？解：①求旋转水的上表面所应满足的方程取水面最低点O 为坐标原点，y 轴竖直向上，r 沿半径方向。

水以角速度ω旋转时，水表面为一旋转对称曲面，取水表面上某一点P 处质量为dm 的水元。

next 水元共受到两个力的作用，作匀速圆周运动。

29：重力, 竖直向下两个力在竖直方向平衡：d·F n ·cos θ= g·dm 水平方向满足：d·F n ·sin θ=ω2r·dm ∴tan θ= ω2r/g drdyan t =θ∵C r g21y 22+=ω假设水面最低点处水膜厚度为h 0，即：r=0 时，y=h 0∴C=h 022h r g21y +ω=∴为一抛物线，所以水表面为旋转抛物面。

Hale Waihona Puke 光波在薄膜上的多次反射与折射
θ
tn
薄膜干涉的复杂性
• 仅仅从一个点光源发出的光波，经过薄膜不同表 面的多次反射就可以在各处进行干涉（非定域）
• 点光源为理想光源，且强度弱，不易观察
S
薄膜干涉的复杂性
• 实际为扩展光源发出的光波，可增强干涉视场强度
• 干涉条纹并非在整个空间可见，而只能在特定的区 域出现（定域干涉）
光波在薄膜上的多次反射与折射仅仅从一个点光源发出的光波经过薄膜不同表面的多次反射就可以在各处进行干涉非定域干涉条纹并非在整个空间可见而只能在特定的区域出现定域干涉所以要采用一定的方法或装置观察某一类光波的干涉两类典型的薄膜干涉一等倾干涉平行光波之间的干涉薄膜上下表面相互平行二等厚干涉光波在薄膜表面处的干涉薄膜上下表面不平行第一列反射光有半波损失而其他的反射光没有半波损失产生了附加相位等效于产生了半波损失
得第N条亮纹的角半径（半径对透镜中心所张开的角，入射角）：
i1N
=
1 n1
n2 Nλ
h
相应的干涉圆环半径：
rN = i1N f
相邻亮纹的角间距：
i1N
=
n2λ
2n12hi1N
相邻亮纹间距：
rN =i1N f
n1 i1 i1 n2 i2
j +1 j
δ i1 ∆i1
第j级亮条纹
λ
2n2h cos i2 = (2 j +1) 2
2n2h sin i2δi2 = λ / 2
δ i2
=
λ
4n2h sin i2
膜厚增大，条纹细锐
中心条纹没有周围细锐
条纹中心疏，周围密
2.6.2. 等厚干涉 （薄膜两表面不平行）

解：由暗纹条件 = 2ne = (2k+1） /2 (k=0,1,2…)
SiO2
Si
M O
知,第9条暗纹对应于k=8,代入上式得 e = (2k+1) /4n = 1.72(m) 所以SiO2薄膜的厚度为1.72 m。
应用2:检测工件平面的平整度
例2 利用空气劈尖的等厚干涉条纹可以检测工 件表面存在的极小的加工纹路， 在经过精密加 工的工件表面上放一光学平面玻璃，使其间形 成空气劈形膜，用单色光照射玻璃表面，并在 显微镜下观察到干涉条纹， 如图所示，试根据干涉条纹 a 的弯曲方向，判断工件表面 b 是凹的还是凸的；并证明凹 ba 凸深度可用下式求得 ：
2k k 1,2,3 2 2n2e 2k 1 k 0,1,2 2
二、劈尖膜 1.装置： 两光学平板玻璃一端接触，另 一端垫一薄纸或细丝 单色、平行光垂直入射 i 0 2 2 2 2e n2 n1 sin i
2n2 e
应用1:测量微小直径，厚度
例1 在半导体元件生产中，为了测定硅片上SiO2薄 膜的厚度，将该膜的一端腐蚀成劈尖状，已知SiO2 的 折射率n =1.46，用波长 =5893埃的钠光照射后，观 察到劈尖上出现9条暗纹，且第9条在劈尖斜坡上端点 M处，Si的折射率为3.42。试求SiO2薄膜的厚度。
ek-1
b ba
h
ek
h
e sin b h sin a
所以:
a h b2
ba
a b
h
ek-1
ek
h
三、牛顿环 1.装置
平板玻璃上放置曲率半径很大的平凸透镜
显微镜 T
L
S
R

大学物理
1
相干条件：频率相同、相位差恒定 、光矢量振动方向平行
相干叠加 I P I1 I 2 2 I1I 2 co s
普通光源 相干光: 同一原子的同一次发光
获得相干光的方法 1. 分波阵面法 2. 分振幅法
杨 氏
δ

r2

r1

xd D
双 缝 干 涉
=

2k
λ 2
,
dmax

kλ 2n2

7.2 107
m
(3) 最外暗环逐渐向外扩大，中心点明暗交替变化，
条纹级数逐渐减少
14
二. 等倾干涉(厚度均匀的薄膜)
两条光线的光程差
S
P
L
E
n2 AB BC n1AD
2n2dcos
考虑到有半波损失
δ

2n2dcosγ

λ 2
iD
n1
a
相邻条纹之间距 asinθ
心心
讨论
2

(1) 空气劈尖顶点处是一暗纹 —— 半波损失 dk

2
dk+1
(2) 可测量小角度θ、微位移 x、微小直径 D、波长 λ 等
(3) 测表面不平整度
等厚条纹
平晶
D
待测工件
9
2. 牛顿环
C
R
光程差
L
2d
2
B
r
A O
S d
R 2 r 2 ( R d ) 2 R>>d, 消去d2 d r 2
2
n1 1 i D
n2
AC

d

尖劈状肥皂膜的干涉图样(左图为倒象)
1. 劈尖干涉 两块平面玻璃片，一端接触，另一端夹一薄纸片，即在两玻 璃片之间形成一劈尖型的空气薄膜，劈尖的夹角 很小（秒数量 级） 当平行单色光垂直玻璃表面入射 时，在空气劈尖上下表面引起的 反射光将形成相干光，
k 加强 2d 减弱 2 (2k 1) 2 k 1,2.... k 0,1,2....
相邻条纹之间距 3.

2
lsinθ


dk dk+1
2

2
空气劈尖顶点处是一暗纹,这是半波损失的一个有力证明。
d 0
/2
设劈尖夹角 ，相邻明条纹(或暗条纹)之间距离 l
2 一定，当 大，l 小，条纹密，当 相当大时，条纹将密得 无法辨认，
则
l sin d k 1 d k
i
A
2
D
C
n1 sin i n2 sin
2n2 AB n1 DC
2

B
d
2n2
2n2
d 2dtg n2 sin cos 2
d (1 sin 2 ) cos 2
2n2 d cos

2
k 加强 2 2d n2 n12 sin 2 i ( 2 k 1 ) 减弱 2 2
k 明纹 光程差 2n2 d （ 2 k 1 ) 暗纹 2

n3
对k值取法 棱边d=0，=0明纹
2n2 d k k应取9，即共有9个间隔，且明纹与暗纹间隔为 4n 2
薄膜厚度： D k 19

d2
8Ra
k
六 注意事项
• 钠光灯不要随意开关 • 读数显微镜的镜筒移至主尺中央（使被测物在 工作区内） • 调节目镜，直至获得清晰的叉丝像 • 将镜筒调到最低（眼睛在镜筒的侧面看），接 近被测物，然后自下而上缓缓提高镜筒（镜筒 只许往上调，不许往下调，以免损坏被测物）， 直到看见清晰的被测物 • 测量中注意“零点”及丝干与螺母之间的空隙 对测量引起的误差
实验18ningboinstitutetechnologyningboinstitutetechnologyzhejianguniversityzhejianguniversity光的干涉实验证实了光的波动性薄膜层的上下表面有一很小的倾角时由同一光源发出的光经薄膜的上下表面反射后在上表面附近相遇时产生干涉在厚度相同的地方形成同一干涉条纹这种干涉就叫等厚干涉牛顿环和劈尖是等厚干涉两个最典型的例子光的等厚干涉原理在生产实践中具有广泛的应用它可用于检测透镜的曲率测量光波波长精确地测量微小长度厚度和角度检验物体表面的光洁度平整度等掌握等厚干涉原理及光束垂直入射时有关劈尖和牛顿圈干涉的计算用等厚干涉法测量曲率半径和薄膜厚度当两片很平的玻璃叠合在一起在一端垫入薄片两玻璃片之间形成一楔形空气薄层空气劈
一 实验目的
• 掌握等厚干涉原理及光束垂直入射 时有关劈尖和牛顿圈干涉的计算 • 用等厚干涉法测量曲率半径和薄膜 厚度 • 进一步学会逐差法处理数据 • 学会使用读数显微镜
二 实验原理
(1) 劈尖 当两片很平的玻璃叠合在一起，在一端垫入薄片， 两玻璃片之间形成一楔形空气薄层（空气劈）。 在单色光垂直照射时，在尖劈膜厚为 e 处，从劈 尖上、下表面反射两条反射光线。 光程差及干涉条件: δ = 2e+λ/2=kλ δ = 2e+λ/2=(2k+1) λ/2

δ1 = 2dn2 cosr = 2d n − n sin r
2 2 2 2 2
P Q 1
= 2d n − n sin i
2 2 2 1 2
半波损失带来的附加光程差 δ 2 :
n1
n2
i D
A
i
2 C
n 1、 1 < n2 ,n3 < n2 或 n1 > n2 ,n3 > n2 、
r
B
d
λ 则： δ2 = 2
2 2 2 1 2
=
550×10−9 m 4 1.332 −12 sin2 30°
= 1.22×10−7 m
λ 垂直入射： 垂直入射： δ = 2n2d + = kλ 2
λ1 = 649.0 nm （k = 1） 红 ）
2n2d ∴λ = 1 k− 2
λ2 = 216.3 nm （k = 2） 不可见光 ）
λ λ 2ndk + = kλ 2ndk+1 + = (k + 1)λ 2 2
∆d
l=
sinθ
=
2nsinθ
≈
2nθ
说明： 说明：
θ 一定，l与λ 的关系 一定， 与 白光照射形成彩纹
1. 条纹级次 k 随着劈尖的厚度而变化，因此这种干 随着劈尖的厚度而变化， 涉称为等厚干涉 等厚干涉。 涉称为等厚干涉。 2、条纹为一组平行与棱边的直条纹。 、条纹为一组平行与棱边的直条纹。 3 . 由于存在半波损失，棱边上为零级暗纹。 由于存在半波损失，棱边上为零级暗纹。 4、厚度 增大，干涉级 增大。 增大， 增大。 、厚度d增大 干涉级k增大 5、相邻条纹等间距。 、相邻条纹等间距。
R
r

等厚干涉明条纹公式等厚干涉明条纹公式，这可是物理学中的一个重要知识点呢！在咱们的物理世界里，等厚干涉明条纹公式就像是一把神奇的钥匙，能帮我们打开探索光的奥秘的大门。

先来说说什么是等厚干涉。

想象一下，有一块楔形的薄膜，或者是两个表面不完全平行的玻璃板夹着一层空气，光透过这些的时候，就会发生等厚干涉现象。

这就好比光在这些地方经历了一场奇妙的冒险。

咱们的等厚干涉明条纹公式是2nh + λ/2 = mλ ，这里的 n 是介质的折射率，h 是薄膜的厚度，λ 是光的波长，m 则是条纹的级数。

记得有一次，我在课堂上给学生们讲解这个公式的时候，有个学生一脸疑惑地问我：“老师，这公式怎么这么复杂，感觉像一团乱麻！”我笑着回答他：“别着急，咱们一步步来，把这团乱麻解开。

” 于是，我拿起一个简单的模型，一块楔形的玻璃片，用一束激光照过去，让同学们亲眼看到那一道道明暗相间的条纹。

“同学们，你们看，这些条纹的出现，就是因为光在不同厚度的地方走过的路程不一样，导致了光的干涉。

”我指着那些条纹说道。

然后，我结合这个模型，一点点地给他们推导公式，解释每个变量的含义。

在实际应用中，等厚干涉明条纹公式用处可大啦！比如说，在检测光学元件表面平整度的时候，通过观察干涉条纹的形状和分布，就能判断出表面是不是平整。

还有在制造高精度的光学仪器时，也得依靠这个公式来保证质量。

再比如，在一些科学研究中，通过精确测量干涉条纹的间距和级数，能够得出微小的厚度变化或者折射率的差异。

这就像是给了科学家们一双超级敏锐的眼睛，让他们能够洞察那些细微到几乎看不见的变化。

学习等厚干涉明条纹公式，不仅仅是记住那几个字母和符号，更重要的是理解背后的物理原理，以及它在实际生活中的应用。

就像我们在生活中，不能只看到表面的现象，而要深入去探究背后的原因和规律。

总之，等厚干涉明条纹公式虽然看起来有点复杂，但只要我们用心去理解，多观察、多思考、多实践，就一定能够掌握它，让它成为我们探索物理世界的有力工具。