离散数学 函数

f3(a)=0, f3(b)=1, f3(c)=0, f4(a)=0, f4(b)=1, f4(c)=1, f7(a)=1, f7(b)=1, f7(c)=0, f8(a)=1, f8(b)=1, f8(c)=1, 但仅有3 个不同的函数, 从B到A但仅有 2 = 9个不同的函数 它们是 到 但仅有 个不同的函数 它们是: f1(0)=a, f1(1)=a, f5(0)=b, f5(1)=b, f7(0)=c, f7(1)=a, f9(0)=c, f9(1)=c. f2(0)=a, f2(1)=b, f6(0)=b, f6(1)=c, f8(0)=c, f8(1)=b, f3(0)=a, f3(1)=c, f4(0)=b, f4(1)=a,
函数的性质(特殊函数 特殊函数) 二、 函数的性质 特殊函数
1、特殊函数 、
定义：设A、B是集合，f 是A到B的函数，对于A 定义： 是集合， 到 的函数， 是集合 的函数 中任意两个元素x1和x2，当x1≠x2时f(x1)≠f(x2), 中任意两个元素 的单射函数。 则称 f 为A到B的单射函数。 到 的单射函数 单射函数要求不同的自变元其函数值也不相同。 射函数要求不同的自变元其函数值也不相同。
函
数
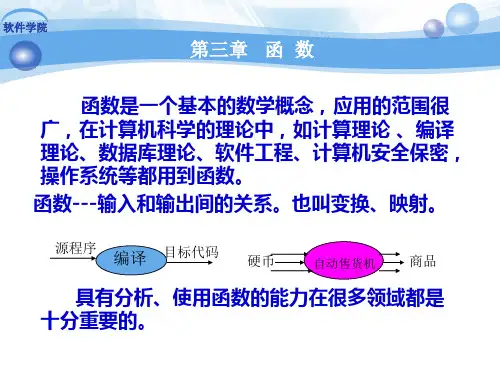
函数是数学中最基本的概念之一， 函数是数学中最基本的概念之一，在高等数学 中，函数的定义域和值域都是在实数集合上讨论 的．本章将函数的概念予以推广，把函数看作是 本章将函数的概念予以推广， 一种特殊的关系， 一种特殊的关系，函数的定义域和值域可以是各 类集合． 类集合．
4.6 函数的定义与性质
2、从 A 到 B 的函数 、
为集合, 定义 设A, B为集合 如果 f 为函数 为集合 domf = A ranf ⊆ B, 为从A到 的函数 的函数, 则称 f 为从 到B的函数 记作 f：A→B. ： 实例 f：N→N, f(x)=2x 是从 N 到 N 的函数 ： g：N→N, g(x)=2也是从 N 到 N 的函数 ： 也是从
f1(x)=1 f2(x)=1 f3(x)=2 f4(x)=2 f5(x)=3 f6(x)=3
f1(y)=2 f2(y)=3 f3(y)=1 f4(y)=3 f5(y)=1 f6(y)=2
2
A到B的单射函数共有 P 到 的单射函数共有 3
= 6 种。
的满射函数是： （2）B到A的满射函数是： ） 到 的满射函数是
判别下列二元关系中哪个能构成函数。 例. 判别下列二元关系中哪个能构成函数。
（1） A={1,2,3},B={4,5,6}, 当a∈A,b∈B，且a<b时，(a,b) ∈f 。 ） ∈ ∈ ， 时 是自然数集合， 的二元关系， （2） 设N是自然数集合，f是N到N的二元关系， ） 是自然数集合 是 到 的二元关系 对于a,b∈ 当 对于 ∈N,当a+b=10时，（a,b）∈f 。 时 ） （3） A＝{2,3,5,}, B={0,1},对于 ∈A,当a为素数时（a,0）∈f. ） ＝ 对于a∈ 当 为素数时（ ） 对于 为素数时 解（1） 显然 f 不是 到B的函数，如对于元素 ∈A， 不是A到 的函数 如对于元素1∈ ， 的函数， ） 中元素1 有（1，4）∈f, (1,5) ∈f, (1,6) ∈f，这表明 中元素 ， ） ，这表明A中元素 个元素有关系， 不是A到 的函数 的函数。 与B中3个元素有关系，所以 f 不是 到B的函数。 中 个元素有关系 中仅有0， ， ， 中元素相关， （2）因为 中仅有 ，1，2，……，10与N中元素相关， ）因为N中仅有 ， 与 中元素相关 所以f 不是N到N的函数。 所以 不是 到 的函数。 的函数 的函数， （3）f 是A到B的函数，且f(2)=f(3)=f(5)=0. ） 到 的函数
例: 设A={x,y}，B={1,2,3}，写出： ， ，写出： (1)A到B的所有单射函数； 到 的所有单射函数 的所有单射函数； (2)B到A的所有满射函数； 到 的所有满射函数 的所有满射函数； (3)B到B的所有双射函数。 到 的所有双射函数 的所有双射函数。 的单射函数为： 解（1） A到B的单射函数为： ） 到 的单射函数为
定义： 是集合， 的函数， 定义： 设A、B是集合，f 是A到B的函数，如果 函数的值域恰好是B 则称 的满射函数。 函数的值域恰好是B，则称f 为A到B的满射函数。 定义： 是集合， 的函数， 定义：设A、B是集合，f 是A到B的函数，如果 f 既是单射函数又是满射函数，则称 f 为A到B的 既是单射函数又是满射函数， 双射函数。双射函数也称为一一对应函数。 双射函数。双射函数也称为一一对应函数。 易知，当A和B是有限集合时， 易知， 是有限集合时， 如果f是 的单射函数，必须有|A|≤|B| |A|≤|B|； 如果 是A到B的单射函数，必须有|A|≤|B|； 如果f是 的满射函数，必须有|A|≥|B| |A|≥|B|； 如果 是A到B的满射函数，必须有|A|≥|B|； 的双射函数，必须有|A|=|B| |A|=|B|。 如果 f 是A到B的双射函数，必须有|A|=|B|。
如集合Ａ＝ 个球， 如集合Ａ＝{b1,b2,b3}，其中 1,B={r,g,w},其中 表示红色，g 表示绿色，w表示白色， 其中r表示红色 表示白色， 其中 表示红色， 表示绿色， 表示白色 的函数， 则 是 到 的函数 令f ={( b1 , r),( b2 , r ),( b3 , g)}.则f是A到B的函数， 函数f表明了第一 表明了第一， 且f(b1)=r, f(b2)=r, f(b3)=g, 函数 表明了第一，二个球 是红色的，第三个球是绿色的。 是红色的，第三个球是绿色的。
从函数的定义可知，函数是一种特殊的二元关系， 从函数的定义可知，函数是一种特殊的二元关系， 其特殊之处在于 : (1) 函数的定义域是集合 而不能是 的某一个真子集 函数的定义域是集合A而不能是 的某一个真子集; 而不能是A的某一个真子集 (2) 对于 ∈A，只能在Ｂ中的一个元素 与之相关， 对于a∈ ，只能在Ｂ中的一个元素b 与之相关， 即不能有f(a)=b ， 又有 又有f(a)=c(b≠c); 即不能有 (3)每一个函数中序偶的第一个元素一定是互不相同的, 每一个函数中序偶的第一个元素一定是互不相同的, 每一个函数中序偶的第一个元素一定是互不相同的 F的这种性质称为单值。 的这种性质称为单值。 例如集合Ａ＝ 例如集合Ａ＝{a,b,c}, B={α，β，γ，ω}， Ａ＝ ， ， ， ， f={(a, β),(b, γ),(c, α)},则f是A到Ｂ的函数， 则 是 到 的函数， 且f(a)= β, f(b)＝γ，f(c)= α。
4、函数的像
定义 设函数 f：A→B, A1⊆A， ： ， 下的像是f(A ∈ 则A1 在 f 下的像是 1) = { f(x) | x∈A1 } 是函数的像。 当A1=A时 ， f(A1) = f(A)=ranf是函数的像。 时 是函数的像 注意： 注意： 是不一样的， 对任意 x∈A, f(x) 与 f(A)是不一样的， f(x)是 ∈ 是不一样的 是 的值， 函数在 x 的值，也可以当作 x在 f 下的像，它是像 在 下的像， 中的一个元素， 集f(A)中的一个元素，即 f(x) ∈ f(A)。 中的一个元素 。
• 函数的定义
– 函数定义 – 从A到B的函数 到 的函数 – 函数的像
• 函数的性质
– 函数的单射、满射、双射性 函数的单射、满射、 – 构造双射函数
• 鸽洞原理
一、 函数的定义
1、函数定义 、
函数也称映射,它表明了两个集合的元素之间的 函数也称映射 它表明了两个集合的元素之间的 对应关系. 对应关系 定义： 和 是集合 是集合， 的二元关系， 定义：A和B是集合，f 是A到B的二元关系，如 到 的二元关系 果f 满足：对于A中每一个元素 ，存在着B中的一个 满足：对于 中每一个元素a，存在着 中的一个 中每一个元素 元素b， 的函数。 元素 ，使(a,b)∈f, 则f为A到B的函数。常把 ∈ 为 到 的函数 常把(a,b)∈f, ∈ 记作f(a)=b, 并称 为自变元或原像，b 为对应于 的 并称a为自变元或原像 为自变元或原像， 为对应于a 记作 函数值或映像。集合 称为函数 的定义域。 函数值或映像。集合A称为函数 f 的定义域。
有关函数的计数问题： 有关函数的计数问题： 是集合， 试问： 例 设A，B是集合，且 A = 3, B = 2 ，试问：从A到B可定义 ， 是集合 到 可定义 多少种不同的函数？ 多少种不同的函数？ 的函数仅含有3个有序对 解：每一个A到B的函数仅含有 个有序对， 每一个 到 的函数仅含有 个有序对， 另外B中两个元素中任意一个都可作为其映象， 另外 中两个元素中任意一个都可作为其映象， 中两个元素中任意一个都可作为其映象 个不同的函数。 故可定义 23 = 8个不同的函数。 一般地， 都是有限集合时， 一般地，当A和B都是有限集合时，且 A = n, B = m ， 和 都是有限集合时 个不同的函数。 则A到B可定义 m 个不同的函数。 到 可定义
是整数集合， 是自然数集合 是 到 的函数 是自然数集合， 的函数， 例： 设I是整数集合，N是自然数集合，f是I到N的函数， 是整数集合 对于任意的整数i， 试判断函数是单射函数、 对于任意的整数 ，f(i)=i2。试判断函数是单射函数、 满射函数、双射函数。 满射函数、双射函数。 不是I到 的单射函数 的单射函数， 解： f 不是 到N的单射函数， 也不是I到N的满射函数， 的满射函数， 也不是 到 的满射函数 也不是I到 的双射函数 的双射函数。 也不是 到N的双射函数。
例：判断下列函数哪些是单射函数、满射函数、双射函数。 判断下列函数哪些是单射函数、满射函数、双射函数。 的函数， （1） 集合 ） 集合A={a,b,c},B={1,2,3,4},f 是A到B的函数， 到 的函数 且f(a)=1，f(b)=2， f(c)=4 。 是正整数集合， 是正偶数集合， （2） 设I+是正整数集合，E+是正偶数集合，f 是I+到E+的 ） 函数，且对于任意的正整数 都有 都有f(n)=2n。 函数，且对于任意的正整数n都有 。 3） I是整数集合 B={0,1}， 是整数集合， I到B的函数 的函数， （3） 设I是整数集合，B={0,1}，f 是I到B的函数，对于 任意的整数i， 为偶数时 为偶数时， 为奇数时， 任意的整数 ，当i为偶数时，f(i)=0；当i为奇数时，f(i)=1。 ； 为奇数时 。 的单射函数； 解（1）f 是A到B的单射函数； ） 到 的单射函数 （2）f 是I+到E+的双射函数 ； ） 的满射函数。 （3）f 是I到B的满射函数。 ） 到 的满射函数