当前位置：文档之家 › 勾股定理说课.ppt

勾股定理说课.ppt

  • 格式：ppt
  • 大小：747.00 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

勾股定理数学优秀ppt课件

勾股定理数学优秀ppt课件
实际应用
在建筑、工程等领域，经常需要利用勾股定理求解直角三角形的边长问题，如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式，则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中，斜边是最长的一边，通过勾股定理可以判断
哪条边是斜边，哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中，直角边的平方和等于斜边的平方，即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形（如正方形、梯形等）的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用，如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础，通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中，勾股定理可以表示 为两个向量的点积等于它们模长的 平方和，这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用，如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一， 也是几何学中的基础概念，对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期，但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国，商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用， 如求解三角形边长、角度、面积等问题，以及力学、光学等领 域的计算。

1.1探索勾股定理说课课件

1.1探索勾股定理说课课件
3题图
研究拓展
• 学生自主操作
• 在给定方格纸中，有一个顶点都在 格点的正方形ABCD，存在一个顶点也 都在格点的直角三角形ABE以其边长AB 为斜边。现分别以三角形的直角边AE、 BE为边长向三角形外作两个正方形，此 时三个正方形的面积有什么关系呢？按 这样的方式又可以作出四个新的小正方 形，这四个小正方形和正方形ABCD的 面积又有什么关系呢？
提出问题
实验探究
教
得出结论
学
例题讲授
过
程
练习反馈
设 计
研究拓展
课堂小结
布置作业
实验探究
• 旧知引出探究方向 • 运算推演进行探究
旧知引出探究方向
a
b
a
a b2 a2 2ab b2
b
运算推演进行探究
直角三角形AOB的两直角边分 别为3和4，三个顶点均在格点上， 分别以三边为边长向三角形外作三 个正方形，试求三个正方形的面积。 （每个方格的边长取“1”）
得出结论
勾股定理（gou-gutheorem)
直角三角形两直角边的平方和等于斜边
的平方.
B
如果直角三角形两直角边分别为a、b,斜
c
边为c，那么 a2 b2 c2
a
C
b
A
或表示为 BC2 AC2 AB2
例题讲授
如图，三角形ABC中，AB⊥AC （1）若BC=25，AB=20，求AC的长度； （2）若BC=10，AB:AC=4：3，求三角形 ABC的面积。
学情分析
• 八年级学生具有一定的几何图形视察能力，抽象思维、逻辑 推理能力也有了一定的发展；
• 所授班级学生基础较好，大部分学生求知欲强，学生希望老 师创设可以引发他们思考的问题情境，让他们进行实际操作 ，给他们发表自己见解和表现自己才华的机会。

勾股定理公开课课件

勾股定理公开课课件
（项明达证明） 项明达:清代数学家
勾股定理的证明
走 进 数 学 史
勾股定理是几何学中的明珠，所以它充满魅力，千百年
来，人们对它的证明趋之若骛，其中有著名的数学家，也有
业余数学爱好者，有普通的老百姓，也有尊贵的政要权贵，
甚至有国家总统。也许是因为勾股定理既重要又简单，更容
易吸引人，才使它成百次地反复被人炒作，反复被人论证。
b
即 直角三角形两直角边的平方和等 于斜边的平方。
表示为：Rt△ABC中，∠C=90°
则 a2 b2 c2
议一议：判断下列说法是否正确,并说明理由： (1)在△ABC中,若a=3,b=4,则c=5 (2)在Rt△ABC中，如果a=3，b=4,则c=5. (3)在Rt△ABC中，∠C=90° , 如果a=3，b=4,则c=5.
快 方法小结: 可用勾股定理建立方程.
！
１、如图,一个长8 米,宽6 米的草地,需在相对角的
顶点间加一条小路,则小路的长为 ( )
C
A.8 米 B.9 米 C.10米 D.14米
化简得： a2 b2 c2
方法三：
c
b b-a c
a c
c
S正
c2
4
1 2
ab
(b
a)2
，
化简得： a2 b2 c2
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
2.求下列直角三角形中未知边的长:
比
5
一
比8
17
看
x
16
x 12
看
x
谁
20
算
得

勾股定理 说课课件(一)

勾股定理 说课课件(一)

教学目标
【知识与技能目标】1、了解勾股定理的文化背景，体验勾理的探索过程，了 解利用拼图验证勾股定理的方法。 2、了解勾股定理的内容。 3、能利用已知两边求直角三角形另一边的长。 【能力与方法目标】1、通过拼图活动，体验数学思维的严谨性，发展形象思维。 2、在探索活动中，学会与人合作，并能与他人交流思维的 过程和探索的结果。
课后习题16.1 1.必做题: 复习巩固 练习 综合运用 习题1.2.3. 2.选做题: 了解勾股定理的多种证明方法.
(根据自己的知识能力掌握情况选择完成.)
如果直角三角形两直角边分别为a、b,
板 书 设 计 ：
斜边为c，那么
c a
┏
b
a2+b2=c2
直角三角形两直角边的平方和 等于斜边的平方.
在我国，把直角三角形的这一个 特佂叫做勾股定理
2、时间分配
1、创设情境
2、实验操作
2分钟
10分钟
3、归纳验证
4、问题解决
10分钟
10分钟
5、课堂小结
6、推荐作业
6分钟
2分钟
A
B
C
A、B、C的面积有什么关系？
SA+SB=SC
直角三角形三边有什么关系？ 两直边的平方和等于斜边的平方
设：直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系？
A a
B b
SA+SB=SC
c
C
a2+b2=c2
如果直角三角形两直角边分别为a、b,
斜边为c，那么
c a
┏
b
a2+b2=c2
勾 股 世 界
我国是最早了解勾股定理的国 家之一。早在三千多年前，周 朝数学家商高就提出，将一根 直尺折成一个直角，如果勾等 于三，股等于四，那么弦就等 于五，即“勾三、股四、弦 五”，它被记载于我国古代著 名的数学著作《周髀算经》中。

数学：18.1勾股定理说课课件(人教新课标八年级下)

数学：18.1勾股定理说课课件(人教新课标八年级下)

教学方法、教学手段的选择

数学是一门培养人的思维，发展人的思维的重 要学科，因此在教学中，不仅要使学生“知其 然”，而且还要使学生“知其所以然”。针对 八年级学生的认知结构和心理特征，本节课选 择“引导探索法”，由浅到深，由特殊到一般 的提出问题,引导学生自主探索，合作交流， 这种教学理念紧随新课改理念，也反映了时代 精神。基本的教学程序是“提出问题-实验操 作 -归纳验证-问题解决-课堂小结-布置作业” 六个方面。
学法指导
新课标明确提出要培养“可持续发展的
学生”，因此教师要有组织、有目的、 有针对性的引导学生并参入到学习活动 中，鼓励学生采用自主探索，合作交流 的研讨式学习方式，培养学生“动手”、 “动脑”、“动口”的习惯与能力，使 学生真正成为学习的主人。
教学程序设计
教学流程图
创 设 情 境 探 索 新 知 实 验 操 作 获 取 新 知 归 纳 验 证 完 善 新 知 问 题 解 决 应 用 新 知 课 堂 小 结 巩 固 新 知
2、再问：
当边长不为整数的直角三角形是否也存在这一结论 呢？投影例题：一个边长分别为1.5，3.6，3.9这种含有 小数的直角三角形，让学生计算。
3.6
3.9
1.5
归纳验证
对于定理的证明，是本堂课的难点，所以我采取 四人小组进行分组讨论，让学生尝试解决。学生讨论 时，我进行巡回指导。如果有些学生感到困难，可以 进行适当点拨, 在这一环节中，学生充分讨论，各抒己 见，充分暴露其思维过程。通过学生的互相讨论，激 发学生的思维活动，可以发现一些解题的方法。 学生代表上台展示拼图结果,对学生的不同解法用 实物投影仪展示出来，选一种方法用电脑显示详细解 题过程.
10分钟
5、课堂小结

人教版八年级下册数学《勾股定理》说课研讨教学复习课件

人教版八年级下册数学《勾股定理》说课研讨教学复习课件

课堂检测
拓广探索题
如图，边长为1的正方体中，一只蚂蚁从顶点A出发沿着
正方体的外表面爬到顶点B的最短距离是（ B ）
A.3
B. 5
C.2
D.1
2
B
C
B
1
1
A
A
2
提示： 由于蚂蚁是沿正方体的外表面爬行的，
故需把正方体展开成平面图形（如图）.
课堂小结
勾股定理 的应用
化非直角三角形为直角三角形 将实际问题转化为直角三角形模型
解：在Rt△AOB中，∵OA=5，OB=4, ∴AB2＝OA2+OB2＝52+42＝41,
∴AB= 41 .
∴A、B两点间的距离为 41 .
课堂检测
4.一木杆在离地面3米处折断，木杆顶端落在离木杆底端4米处. 木杆折断之前有多高？
解：由题意可知，在Rt△RPQ中， ∵PR=3，PQ=4，
∴RQ2＝PR2+PQ2＝32+42＝25, ∴RQ＝5，PR+RQ＝3+5＝8.
小于AC即可. 3.怎样判定这块木板能否通过木框？
求出斜边的长，与木板的宽比较.
探究新知
解：在Rt△ABC中，根据勾股定理， AC2=AB2+BC2=12+22=5． AC= 5 ≈2.24． 因为AC大于木板的宽2.2 m，所
以木板能从门框内通过．
巩固练习
如图，池塘边有两点A，B，点C是与BA方向成直角的AC方 向上一点，测得BC=60 m，AC=20m.求A，B两点间的距离
1.求出下列直角三角形中未知的边.
B
B
AC=8 6
C
10
8
15
A
C

《勾股定理》PPT优质课件(第1课时)

《勾股定理》PPT优质课件(第1课时)

A． 3
B．3
C． 5
D．5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12，则斜边的
长为（ C）
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17，一条直角边长为15，则
另一直角边长为（ A ）
A.8
B.40
C.50
D.36
3.在Rt△ABC中，∠C=90°，若a︰b=3︰4，c=100，则 a= _6_0___，b = __8_0___.
课堂检测
4．如图，所有的四边形都是正方形，所有的三角形都是直角三角 形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面 积之和为_____4_9_____cm2 ．
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：
当AB为斜边时，如图，BC 42 32 7;
形，拼成一个新的正方形.
探究新知 剪、拼过程展示：
b
a ca
朱实
b 朱实 黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实 朱实
a
朱实
证明：∵S大正方形＝c2， S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
探究新知
毕达哥拉斯证法：请先用手中的四个全等的直角三角形按图 示进行拼图，然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152，

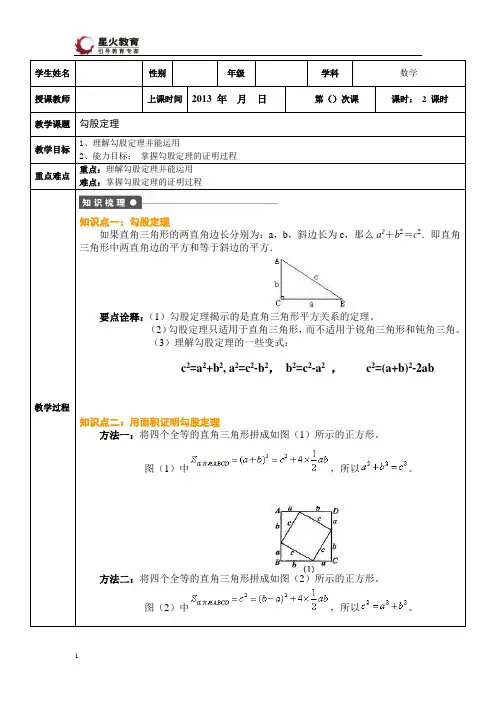
(完整版)勾股定理课件

(完整版)勾股定理课件

学生姓名性别年级学科数学授课教师上课时间2013 年月日第（）次课课时：2 课时教学课题勾股定理教学目标1、理解勾股定理并能运用2、能力目标：掌握勾股定理的证明过程重点难点重点：理解勾股定理并能运用难点：掌握勾股定理的证明过程教学过程知识点一：勾股定理如果直角三角形的两直角边长分别为：a，b，斜边长为c，那么a2＋b2＝c2．即直角三角形中两直角边的平方和等于斜边的平方．要点诠释：（1）勾股定理揭示的是直角三角形平方关系的定理。

（2）勾股定理只适用于直角三角形，而不适用于锐角三角形和钝角三角。

（3）理解勾股定理的一些变式：c2=a2+b2, a2=c2-b2，b2=c2-a2，c2=(a+b)2-2ab知识点二：用面积证明勾股定理方法一：将四个全等的直角三角形拼成如图（1）所示的正方形。

图（1）中，所以。

方法二：将四个全等的直角三角形拼成如图（2）所示的正方形。

图（2）中，所以。

知识点三：勾股定理的作用1．已知直角三角形的两条边长求第三边；2.已知直角三角形的一条边，求另两边的关系；3．用于证明平方关系的问题；4．利用勾股定理，作出长为的线段。

(3)在理解的基础上熟悉下列勾股数满足不定方程x2+y2=z2的三个正整数，称为勾股数（又称为高数或毕达哥拉斯数），显然，以x,y,z为三边长的三角形一定是直角三角形。

熟悉下列勾股数，对解题是会有帮助的：①3、4、5②5、12、13；③8、15、17；④7、24、25；⑤10、24、26；⑥9、40、41．如果(a,b,c)是勾股数，当t>0时，以at,bt,ct为三角形的三边长，此三角形必为直角三角形。

经典例题透析类型一：勾股定理的直接用法1、在Rt△ABC中，∠C=90°(1)已知a=6，c=10，求b，(2)已知a=40，b=9，求c；(3)已知c=25，b=15，求a.举一反三【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?类型二：勾股定理的构造应用2、如图，已知：在中，，，. 求：BC的长.举一反三【变式1】如图，已知：，，于P. 求证：.【变式2】已知：如图，∠B=∠D=90°，∠A=60°，AB=4，CD=2。

冀教版八年级上册数学《勾股定理》说课研讨复习教学课件

冀教版八年级上册数学《勾股定理》说课研讨复习教学课件
能够成为直角三角形三条边长的 三个正整数
建模思想，即将实际问题转化为 数学问题
D
CD长为3尺，点B被红莲吹斜后花朵的位置，
BC部分长6尺.设水深AC为x尺.
C
B 在Rt△ABC中，
∴AC2+BC2=AB2（勾股定理）.
又∵AB=AD=（x+3）尺,
A
∴（x+3）2=x2+62，化简解得x=4.5.
答：湖水深4.5尺.
知识讲解
归纳：勾股定理的实际应用的一般步骤：
（1）读懂题意，分析已知、未知间的关系； （2）构造直角三角形； （3）利用勾股定理等列方程； （4）解决实际问题.
BaC
勾股定理的逆定理是直角三角形的判定定理，即已知三角形的三边长， 且满足两条较小边的平方和等于最长边的平方，即可判断此三角形为直角 三角形 ，最长边所对应的角为直角.
知识讲解
例1 判断由线段a，b，c组成的三角形是不是直角三角形?
(1) a=15，b=8，c=17; (2) a=13，b=14，c=15.
基本思想方法：勾股定理把“形”与
C
“数”有机地结合起来，即把直角三角
形这个“形”与三边关系这一“数”结
A
B
合起来，它是数形结合思想的典范．
知识讲解
C 解：在△ABC中，
∵∠ACB=90°，
A
B
∴AC2+BC2=AB2(勾股定理).
∵AB=200 m，BC=160 m，
AC AB2 BC2 2002 1602 120 (m). 答：点A和点C间的距离是120 m.
a勾
b2 = c2 - a2
新课导入
观看下面同一根长竹竿以三种不同的方式进门的情况，

(精选幻灯片)勾股定理ppt课件

(精选幻灯片)勾股定理ppt课件
2 2 22
“总统证法”． 比较上面二式得 c2=a2+b2
16
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
17
做一做：
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
b c
a2+b2=c2吗？
• 1881年，伽菲尔 德就任美国第二
A b 1 E aB ∵ S梯形ABCD= 2 a+b2
十任总统.后来， 1
人们为了纪念他 对勾股定理直观、 简捷、易懂、明
= (a2+2ab+b2) 2
又∵ S梯形 ABCD=S
AED+S
EBC+S
CED
了的证明，就把 这一证法称为
1 1 11 = ab+ ba+ c2= (2ab+c2)
33
34
C A
（2）在图2-2中，正 方形A，B，C中各含 有多少个小方格？它 们的面积各是多少？
B C
图2-1
A
（3）你能发现图2-1 中三个正方形A，B， C的面积之间有什么
B 图2-2
关系吗？
（图中每个小方格代表一个单位面积） SA+SB=SC
即：两条直角边上的正方形面积之和等于
斜边上的正方形的面积
3
s1 s2
s3
返 拼回 图 4
合作 & 交S流1+☞S2=S3
a等²+腰a直²=角c三²角形两直角边

北师大版八年级上册数学《一定是直角三角形吗》勾股定理PPT说课教学

北师大版八年级上册数学《一定是直角三角形吗》勾股定理PPT说课教学

D
C
A
B
1- 16
D
1 3
C
45 1
A3 B 2
1- 17
解： ∵在R
AB2+AD2=9+16=25=BD2 ∴△ABD是直角三角形，∠A是直角 ∵在△BCD中， BD2+BC2=25+144=169=CD2 ∴△BCD是直角三角形，∠DBC是直角
因此这个零件符合要求。
随堂练习
1.如果三角形的三边长a＜b ＜ c满足 _______________，那么这个三角形是直角三角形； 2.写出三组勾股数： _______________________________; 3.一艘帆船在海上航行，由于风向的原因，帆船 先向正东方向航行9千米，然后向正北方向航行40 千米，这时它离开出发点_________千米。
5. 以∆ABC的三条边为边长向外作正方形, 依次得到的面
积是25, 144 , 169, 则这个三角形是_直___角__三角形。
6. 四边形ABCD中已知AB=3, BC=4,
CD=12, DA=13, 且∠ABC=900,求这个
D
四边形的面积。
A
B
C
7.请你写出三组勾股数。
8.一组勾股数的倍数一定是勾股数吗？为什么?
4.下列几组数能否作为直角三角形的三边长？ 说说你的理由。
√ √ （1）9，12，15； （2）15，36，39；
（3）12，35，36； （4）12，18，22。
5.判断下列哪组数是勾股数： （1）6，7，8； （2）8，15，6；
√（3）a=n2-1，b=2n，c=n2+1 （n＞1） √（4）a=m2-n2，b=2mn，c=m2+n2 （m＞n＞0）

勾股定理ppt课件

勾股定理ppt课件

创设情境 数学是科技发展中最重要的学科，2002年全球最顶级数学家大 会在北京召开，大会会徽是：
赵爽弦图
数学文化 赵爽，名婴，字君卿，是我国三国时期杰出的数学家， 他在注解《周髀算经》时给出的这个图.
创设情境 请你观察这个图中有哪些基本几何图形？2002年的数学家大会为 什么用这个图作为会徽呢？
继续探究
1.如图，表格中左、右各有一组图，每组图中的三个正方形的面积分 别是多少，它们之间有什么关系？（设表格中每个小正方形面积为1）
C A
B
C A
B
继续探究 2.观察图形，请完成下面表格：
两个图中正 方形C的面积 如何求呢？
项目
左图 右图 A、B、C 面积关系
A的面积 4 16
B的面积 9 9
A
8
B 6
C
应用新知
例2 如图，图中所有的三角形都是直角三角形，四边形都是正方形，已知正方形 B，D的边长分别是16，12，SE=625，S1=400，求正方形A、C的边长. 解：依题意，得SB=162=256，SD=122=144， ∵S1=SA+SB且S1=400， ∴SA=S1-SB=400-256=144， ∴正方形A的边长为 144 12， ∵SE=S1+S2且SE=625，S1=400， ∴S2=SE-S1=625-400=225， ∵S2=SC+SD，∴SC=S2-SD=225-144=81， ∴正方形C的边长 81 9 .
证明2： 如图，四个全等直角三角形拼成
如图所示的正方形，直角边为a、
b，斜边为c. S四个直角三角形面积和= 4 1 ab 2ab，
2
S四个直角三角形面积和=(a+b)2-c2

《勾股定理》数学教学PPT课件(10篇)

《勾股定理》数学教学PPT课件(10篇)
= (DE+CE)·( DE- BE)
=BD·
CD.
D
B
E
C
课堂小
结
利用勾股定理解
决实际问题
勾股定理
的应用
构造直角三角形
解决实际问题
第十七章 勾股定理
17.1 勾股定理
第3课时
利用勾股定理作图和计算
知识要点
1.勾股定理与数轴、坐标系
2.勾股定理与网格
3.勾股定理与几何图形
新知导入
想一想：
我们知道数轴上的点有的表示有理数，有的表示无理数，你
能在数轴上画出表示 13 的点吗？
如果能画出长为 13 的线段，就能在数轴上画出表示 13 的
2
点.容易知道，长为
的线段是两条直角边的长都为1的直角三
角形的斜边.
长为 13 的线段能是直角边的长为正整数的直角三角形的
斜边吗？
新知导入
想一想：
利用勾股定理，可以发现，直角边的长为正整数2, 3
知识
的直角三角形的斜边长为
AC2+BC2=AB2
由上面的例子，我们猜想：
命题1 如果直角三角形的两条直角边长分别为a,b，斜边
长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
a
c
b
课程讲授
1
勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c
证明：∵S大正方形＝c2，
S小正方形＝(b-a)2,
b
a
b-a
例 如图是由4个边长为1的正方形构成的“田字格”，只用没有刻
度的直尺在这个“田字格”中最多可以作出长度为
8
_____条．

勾股定理的应用PPT课件

勾股定理的应用PPT课件

2
0.3
0.2
A
B
A
B
C
2m
(0.2×3＋0.3×3)m
选作： 1. 如图，长方形中AC=3,CD=5,DF=6,求蚂蚁沿表面从A爬到F的最短距离.
3
5
6
A
C
D
E
B
F
已知：如图，在△ABC中，∠ACB＝90º，AB＝5cm，BC＝3cm，CD⊥AB于D，求CD的长.
已知：如图，在 中， ，是 边上的中线， 于， 求证：.
如图，将长为10米的梯子AC斜靠 在墙上，BC长为6米。
A
B
C
10
6
(1)求梯子上端A到墙的底端B的距离AB。
（2）若梯子下部C向后移动2米到C1点，那么梯子上部A向下移动了多少米？
A1
C1
2
一位工人叔叔要装修家，需要一块长3m、宽2.1m的薄木板，已知他家门框的尺寸如图所示，那么这块薄木板能否从门框内通过?为什么?
B
C
A
3
2
1
B
C
A
(1)当蚂蚁经过前面和上底面时，如图，最短路程为
解:
A
B
2
3
A
B
1பைடு நூலகம்
C
AB＝
＝
＝
(2)当蚂蚁经过前面和右面时，如图，最短路程为
A
B
3
2
1
B
C
A
AB＝
＝
＝
(3)当蚂蚁经过左面和上底面时，如图，最短路程为
A
B
AB＝
＝
＝
3
2
1
B
C
A
2.如图，是一个三级台阶，它的每一级的长、宽、高分别为2m、0.3m、0.2m，A和B是台阶上两个相对的顶点，A点有一只蚂蚁，想到B点去吃可口的食物，问蚂蚁沿着台阶爬行到B点的最短路程是多少？

勾股定理说课课件Microsoft PowerPoint 演示文稿

勾股定理说课课件Microsoft PowerPoint 演示文稿

• （1）动手制作：每人用硬纸板/片制作四个两条 1 动手制作：每人用硬纸板/ 直角边分别为6cm 8cm的直角三角形模型 6cm和 的直角三角形模型； 直角边分别为6cm和8cm的直角三角形模型；边长 分别为2cm 6cm、8cm、10cm的正方形各一个 2cm、 的正方形各一个。 分别为2cm、6cm、8cm、10cm的正方形各一个。 • （2）事先准备好的标有统一单位的直角坐标系。 事先准备好的标有统一单位的直角坐标系。 • （3）学生分史故事，每组至少要搜集3 股定理的历史故事，每组至少要搜集3个不同的故 事。
GOUGUDINGLI
勾 股 定 理
课内探究
一、填空： 填空：
1、Rt△ABC中，∠C＝ 90°a=6，c=10。求b＝＿＿＿＿ 、 △ 中 ＝ ° ， 。 ＝＿＿＿＿ 2、已知：已知直角三角形的两边长分别为 、4，求第三边 、已知：已知直角三角形的两边长分别为3、 ， 长为＿＿＿＿＿ 长为＿＿＿＿＿
GOUGUDINGLI
勾 股 定 理
目标定位 .重点 重点、 2 .重点、难点
教学重点： 教学重点：勾股定理的探索及简单应用 . 教学难点： 教学难点：勾股定理的证明 . 突破方法：采用学生动手拼图， 突破方法：采用学生动手拼图，自主探 合作交流法. 索，合作交流法.
GOUGUDINGLI
勾 股 定 理
勾 股 定 理
优胜小组评选： 优胜小组评选： G1： ： G2: G3: G4: G5: G6: G7: G8:
板书设计
§5.2 勾股定理
数学表达式
学生习题板书： 学生习题板书：
学生习题板书： 学生习题板书：
GOUGUDINGLI
诚请各位专家同行指导
2010-7

勾股定理ppt

勾股定理ppt
勾股定理与两直线垂直的关系
如果一个直角三角形的斜边为c，其中一条直角边为a，另一条直角边为b，那么 以a和b为直径的圆与斜边c相切。
勾股定理与三角函数的联系
勾股定理与正弦函数的关系
正弦函数是三角函数的一种，它表示直角三角形中锐角度数 的对边与斜边的比值，即sinA=a/c。
勾股定理与余弦函数的关系
勾股定理的逆定理
逆定理的表述
勾股定理的逆定理是指如果三角形的三边长a、b、c满足a²+b²=c²，那么这 个三角形是直角三角形。
逆定理的证明方法
勾股定理逆定理的证明方法比较简单，可以通过三角形全等的判定方法“边 边边”进行证明。也可以通过反证法进行证明，假设三角形不是直角三角形 ，则可以推导出矛盾的结果，从而证明了逆定理的正确性。
间的距离、求圆的直径等。
勾股定理在日常生活中的应用
建筑学
勾股定理在建筑学中有着广泛的应用，例如确定建筑物的结构、设计建筑物的外 观等。
制作直角工具
勾股定理可以用来制作直角工具，例如勾股尺、勾股定理板等。
勾股定理在金融和投资领域的应用
确定投资组合
在金融和投资领域中，勾股定理可以用来确定投资组合，以 实现最大收益和最小风险。
勾股定理的一般形式
勾股定理不仅仅适用于直角三角形，对于一般的三角形同样适用，其一般形 式为：c² = a² + b² - 2abcosθ，其中θ为两直角边的夹角。
勾股定理与平面几何的联系
勾股定理与三角形面积的关系
勾股定理可以用来求三角形的面积，其中一条直角边为底边，另外两条为高，三 角形的面积为1/2底边乘以高。
学习技巧
学习技巧包括制定学习计划、合理安排时间、掌握学习重点 和难点、积极参与课堂讨论等。同时，需要注重实践和应用 ，将理论知识应用到实际问题的解决中。

勾股定理说课稿ppt课件

勾股定理说课稿ppt课件

（二）学情分析
八年级学生已初步具有几何图形的 观察，几何证明的理论思维能力。希 望老师预设便于他们进行观察的几何 环境，给他们发表自己见解和表现自 己才华的机会，希望老师满足他们的 创造愿望，让他们实际操作，使他们 获得施展自己创造才能的机会。
580 630
（三）教学方法
数学是一门培养人的思维,发展人的思维的重要学 科,因此,在教学中,要展现获取知识和方法的思维过 程, 针对八年级学生的知识结构和心理特征，本节 课采取引导探索法，由浅入深，由特殊到一般地提 出问题。以导为主,采用设疑的形式，让学生通过观 察、分析、讨论、操作、归纳，理解定理，提高学 生动手操作能力，以及分析问题和解决问题的能力。 5 使学生得到获得新知的成功感受，从而激发学生钻 m 研新知。并利用教具与多媒体进行教学。
2m
活动2、探索勾股定理
探究一（观察特例→发现新知）
{问题一}：在图中你能发现哪些基本图形？ {问题二}：与等腰直角三角形相邻的正方形面积之间 有怎样的关系？ {问题三}：如图，每个小方格的面积为1个单位，你能 写出正方形A、Ｂ、Ｃ的面积吗？ {问题四}：由此你可以得出等腰直角三角形三边存在着一种怎样特殊的数量关 系吗？ 学生在独立探究的基础上观察图片，计算面积，分组交流， 猜想和归纳。 教师参与学生小组活动，指导，倾听学生交流。 设计意图：通过讲传说故事来激发学生学习兴趣，引导学生进入学习状态。 学生会很积极的投入到探索这个问题的实践中。 “问题是思维的起点”，通过层层设问，引导学生发现新知。由正方形的面 积等于边长的平方归纳出：等腰直角三角形两条直角边的平方和等于斜边的平 方。 {问题五}：等腰直角三角形三边具有这样的特殊关系，那么一般的直角三角形 呢？
B
Ｂ
350 A

《勾股定理》PPT

《勾股定理》PPT
综合题：3.如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1，求 △ABC的周长．
小贴士
为什么叫勾股定理这个名称呢？ 在中国古代，人们把弯曲成直角的手臂的上半部分称 为“勾”，下半部分称为“股”.我国古代学者把直角三 角形较短的直角边称为“勾”，较长的直角边称为 “股”，斜边称为“弦”.由于命题1反映的正好是直 角三角形三边的关系，所以叫做勾股定理.
勾
股
勾2+股2=弦2 国外又叫毕达哥拉斯定理
当BC为斜边时，如图，BC 42 32 5.
B B
4
3
C 图 A
4
A
3
图
C
归纳 当直角三角形中所给的两条边没有指明是斜边或 直角边时，其中一较长边可能是直角边，也可能是斜 边，这种情况下一定要进行分类讨论，否则容易丢解.
当堂练习
1.下列说法中,正确的是
（ C）
A.已知a,b,c是三角形的三边，则a2+b2=c2
新知应用
例1 如图，在Rt△ABC中， ∠C=90°.
（1）若a=b=5,求c;
B
（2）若a=1,c=2,求b.
a
解：(1)在Rt△ABC中， ∠C=90°
C
c a2 b2 52 52 50 5 2;
c
A
b
(2)在Rt△ABC中， ∠C=90°
b c2 a2 22 12 3.
注意：1.看好哪个角是直角,选择正确的公式来求边长
C
问题2 图中正方形A、B、C所围成的等腰直角三角 形三边之间有什么数量关系？
AB C
S正方形A S正方形B S正方形C
一直角边2 +
另一直角边2 =
斜边2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
新课标明确提出要培养“以学生为主体的学习理念” ，因此教师要有组织、有目的、有针对性的引导学生 并参入到学习活动中，鼓励学生采用自主探索，合作 交流的研讨式学习方式，培养学生“动手”、“动脑 ”、“动口”的习惯与能力，使学生真正成为学习的 主人。
四、教学过程
（一）创设情境，由故事引入，引发兴趣
2、教学目标
知识目标：
（1）掌握勾股定理并理解勾股定理反映的直角三角形三
遍之间的数量关系（2）学会运用勾股定理求解和证明
能力目标：
（1）通过探索发现勾股定理的过程，发展学生的合理推
理意识，主动探究的习惯（2）通过拼图在勾股定理证明中渗透的数形结合的 思想方法，增强学生的逻辑思维能力（3）通过求解例题提高学生的运算能力
数学是一门培养人的思维，发展人的思维的重要学科 ，因此在教学中，不仅要使学生“知其然”，而且还 要使学生“知其所以然”。针对初中年级学生的认知 结构和心理特征，本节课选择“引导探索”的教学方 法，由浅到深，由特殊到。引导学生自主探索，合作 交流，这种教学理念紧随新课改理念。基本的教学程 序是“创设情景-引入课题-证明定理-巩固练习-课堂 小结-布置作业”六个方面。
勾股定理
说 课 内 容
教材分析
教学重难点
教学方法与手引入课题 证明定理 巩固练习 课堂小结 布置作业
一、教材分析
1、教材内容的地位及作用
这节课是九年制义务教育课程标准实验教科书八 年级第一章第一节探索勾股定理第一课时，教学 内容是勾股定理公式的推导、证明及其简单的应 用。勾股定理是几何中几个重要定理之一，它揭 示的是直角三角形中三边的数量关系。它在数学 的发展中起过重要的作用，在现时世界中也有着 广泛的作用。学生通过对勾股定理的学习，可以 在原有的基础上对直角三角形有进一步的认识和 理解.
情感目标：
（1）通过自主学习体验解决问题方法的多样性，体验数
学之美探究之趣（2）通过对问题的探索，培养学生的合作交流意识和探索精 神（3）通过获得成功的经验和克服困难的经历，增进数学学习的信心
二、教学重点与难点
教学重点：运用勾股定理来解决一些简单的问题
教学难点：勾股定理的证明
三、教学方法与教学手段
1、你这节课学到了什么知识点？ 2、你学会了什么学习方法？
（六）作业
1、必做题：书课后习题 2、选做题：勾股定理的其他证明方法
五、教学反思
运用多媒体教学的优缺点 如何引起学生的兴趣 勾股定理的证明
谢谢！ 再见
（三）拼图证明勾股定理
方法一：
A
a
b
B
C
D
方法二: H
c
G
E
F
（四）例题
课堂练习，使学生巩固基础知识，强化提 高解题能力
1 .在Rt△ABC ,∠C=90 °. (1) 已知：a=6，ｂ=8，求c； （2）已知a=5，b=12，求c (3) 已知：c=13，b=12，求a；
（五）课堂小结
1、在中国，大约公元前1世纪前后成书的《周髀算经》里记 载着 3000多年前有个叫商高的人对周公说，把一根直尺折成直 角，两端连接得到一个直角三角形，如果勾是3，股是4，那么 弦等于5。
2、在国外，尤其在西方，勾股定理通常被称为毕达哥拉斯定 理．这是由于，他们认为最早发现直角三角形具有“勾2+股2= 弦2”这一性质并且最先给出严格证明的是古希腊的数学家毕达 哥拉斯．
（二）引入知识点
由特殊到一般进行探索
等腰直角三角 形三边关系
一般直角三角 形三边关系
1、特殊
等 腰 直 角 三 角 形
网格画图 面积计算 面积关系 得出结论
2、一般
一 般 直 角 三 角 形
网格画图 面积计算 面积关系 得出结论
得出结论：直角三角形两直角边的平方和 等于斜边的平方。
勾股定理：如果直角三角形两直角边分别 为a、b,斜边为c，那么a2+b2=c2