当前位置：文档之家 › 勾股定理说课PPT课件

勾股定理说课PPT课件

  • 格式：ppt
  • 大小：107.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

勾股定理说课.ppt

勾股定理说课.ppt
新课标明确提出要培养“以学生为主体的学习理念” ，因此教师要有组织、有目的、有针对性的引导学生 并参入到学习活动中，鼓励学生采用自主探索，合作 交流的研讨式学习方式，培养学生“动手”、“动脑 ”、“动口”的习惯与能力，使学生真正成为学习的 主人。
四、教学过程
（一）创设情境，由故事引入，引发兴趣
2、教学目标
知识目标：
（1）掌握勾股定理并理解勾股定理反映的直角三角形三
遍之间的数量关系（2）学会运用勾股定理求解和证明
能力目标：
（1）通过探索发现勾股定理的过程，发展学生的合理推
理意识，主动探究的习惯（2）通过拼图在勾股定理证明中渗透的数形结合的 思想方法，增强学生的逻辑思维能力（3）通过求解例题提高学生的运算能力
数学是一门培养人的思维，发展人的思维的重要学科 ，因此在教学中，不仅要使学生“知其然”，而且还 要使学生“知其所以然”。针对初中年级学生的认知 结构和心理特征，本节课选择“引导探索”的教学方 法，由浅到深，由特殊到。引导学生自主探索，合作 交流，这种教学理念紧随新课改理念。基本的教学程 序是“创设情景-引入课题-证明定理-巩固练习-课堂 小结-布置作业”六个方面。
勾股定理
说 课 内 容
教材分析
教学重难点
教学方法与手引入课题 证明定理 巩固练习 课堂小结 布置作业
一、教材分析
1、教材内容的地位及作用
这节课是九年制义务教育课程标准实验教科书八 年级第一章第一节探索勾股定理第一课时，教学 内容是勾股定理公式的推导、证明及其简单的应 用。勾股定理是几何中几个重要定理之一，它揭 示的是直角三角形中三边的数量关系。它在数学 的发展中起过重要的作用，在现时世界中也有着 广泛的作用。学生通过对勾股定理的学习，可以 在原有的基础上对直角三角形有进一步的认识和 理解.

勾股定理说课PPT

勾股定理说课PPT

1
说教材
二、教学目标
１．知识技能 知道勾股定理的由来，能说出勾股定理的内容，理解并掌握勾股定理证 明方法，并能进行简单的计算运用 ２．过程性目标 让学生经历“观察－猜想－归纳－验证”的数学过程，并从中体会数形 结合、转化及从特殊到一般的数学思想。培养学生观察、比较、分析、推理 的能力。 ３．情感、价值观目标 介绍我国古代在研究勾股定理方面取得的伟大成就，激发学生热爱祖国与 热爱祖国悠久文化的思想感情，培养他们的民族自豪感在探索问题的过程中， 培养学生的合作交流意识和探索精神。 重点：勾股定理的探索与发现过程
勾
股
自豪的数学史，激发学生的 数学热情以及民族自豪感。
5
说作业的安排和板书设计
1、必 做题 ： 教科书P68 练习1,2 ． 2 、选做题 ： 通 过上网、查看 书籍 ，了解勾股定理的 文化背景和收集有关勾股定理的证明方法 ，下节课展示 交流
必做题是为了巩固学生今天所学的内容 选做题给学生留有继续学习的空间和兴趣 ，提高学生的 实践 能力 与创新 意识 ，让每个同学都能获得良好的数 学教育，不 同的学生在数学上得到不同的发展
设计意图： 1、数格子已经蕴含一定的割补思想方法，给同学们找出其他方法一定 的启发 2、通过对已知公式的回忆，引领同学们利用先知探究未知，以便得 出所要结论，强调知识之前的联系性，并体现了一定的数形结合思想。 3、分小组讨论加强了同学之间的合作与交流
p
R
Q
割
补
学生通过计算可得到P+Q=R，继而得到a² +b² =c² 从探究边的关系转为探究正方形面积之间的关系， 从边不在格子上的图形，转变为可计算格点的图形
(A) 斜边为5 ( C )斜边为 25 （ B ）三角形的周长为 12

勾股定理说课PPT课件

勾股定理说课PPT课件
观察猜测 动手操作 交流讨论 归纳总结
教学程序设计
教学流程图
回顾小结深化新知 学以致用拓展新知 学生活动验证新知 拼图验证归纳新知 观察特例发现新知 创设情境引入新课
《 勾股定理》说课
《 勾股定理》说课
教学程序设计
第一环节 创设情境 引入新课
赵爽弦图 中国——赵爽
北京欢迎您！
18.1勾股定理（1）
勾股命定题理1： 如果直角三角形的两直角边长分别为
, a，斜b 边长为 ，那c 么 a2 b2 c2.
勾
弦
c
a
股bΒιβλιοθήκη 股世界两千两多千多年年前前，，古古希希腊有腊个有哥拉个毕达哥拉斯 学斯学派派，，他他们们首首先发先现发了勾现股了定勾理，股因定此 理，因此在 在国国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 定理理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯，1学95派5 ，1955年 年希希腊腊曾曾经经发发行行了一了枚一纪念枚票纪。念邮票。
结论：
a2 b2 c2
a
b c
a
c
b
(a b)2 c2 4 1 ab 2
a2 b2 c2
《 勾股定理》说课
教学程序设计
第五环节 学以致用 拓展新知
基础训练
1、分别求出图中A、B的面积
A
81
144
B 196
289
基础训练
2 .求出下列直角三角形中未知边的长度.
A
A
B
17
3 C4
B
《 勾股定理》说课
教学程序设计
第四环节 学生活动 验证新知
动y动=手0
尝试用下面四个全等的直角三角形围成一个 正方形，然后通过面积分割法和整体计算法分别 求出正方形的的面积，看看你有什么发现。

勾股定理 说课ppt

勾股定理 说课ppt
观察特例 发现新知
(1)等腰直角三角形都有上述性质吗?观察下图，并填表：
A的面积 B的面积 C的面积 (单位面积) (单位面积) (单位面积) 图1 图2
9 4
9 4
18 8
(2)用语言描述你发现的等腰直角三角形的性质。 由正方形面积之间的数量关系引出直角三角形三边之间 的数量关系，让学生充分感受不同量之间的相互转化，由 学生总结出结果，有利于培养学生的语言表达能力．
我国有资料记载的 让学生模拟数学家的 对勾股定理的最早 思维方式和思维过程, 亲身体验勾股定理的 证法.表现了我国 探索与验证，使学生 古人对数学的钻研 对定理的理解更加深 刻，体会数形结合思 精神和聪明才智. 它是我国古代数学 想，发展创造性思维 的骄傲．正因如此， 能力.活动中教师应 重点关注：学生能否 这个图案被选为 进行合理的分割，对 2002年在北京召 不同层次的学生有针 开的国际数学家大 对性地给予分析、帮 助。教师对比介绍古 会的会徽．
☆☆☆ 猜想探索 得出定理 ☆☆☆
观察特例 发现新知
你能发现图中的等腰直角三角形有什么性质吗？
留给学生充分的思考时间，学生交流合作，得出结 论．通过让学生观察计算，发现等腰直角三角形，满足两直 角边的平方和等于斜边的平方。让学生亲历发现、探究结论 的过程，体会数形结合的思想．
☆☆☆ 猜想探索 得出定理 ☆☆☆
在本次活动中，教师应关注：①能否通过拼图计算面积的方 法得到直角三角形的三边关系．②学生能否积极主动地参与拼 图活动．让学生通过拼图、分析面积之间的关系，证明直角三 角形的三边关系，培养学生的动手操作能力和创新意识．
☆☆☆ 动手实践 加深理解 ☆☆☆ 试一试：剪两刀拼成一个正方形。 赵爽弦图 创设目的
说课

(精选幻灯片)勾股定理ppt课件

(精选幻灯片)勾股定理ppt课件
2 2 22
“总统证法”． 比较上面二式得 c2=a2+b2
16
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
17
做一做：
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
b c
a2+b2=c2吗？
• 1881年，伽菲尔 德就任美国第二
A b 1 E aB ∵ S梯形ABCD= 2 a+b2
十任总统.后来， 1
人们为了纪念他 对勾股定理直观、 简捷、易懂、明
= (a2+2ab+b2) 2
又∵ S梯形 ABCD=S
AED+S
EBC+S
CED
了的证明，就把 这一证法称为
1 1 11 = ab+ ba+ c2= (2ab+c2)
33
34
C A
（2）在图2-2中，正 方形A，B，C中各含 有多少个小方格？它 们的面积各是多少？
B C
图2-1
A
（3）你能发现图2-1 中三个正方形A，B， C的面积之间有什么
B 图2-2
关系吗？
（图中每个小方格代表一个单位面积） SA+SB=SC
即：两条直角边上的正方形面积之和等于
斜边上的正方形的面积
3
s1 s2
s3
返 拼回 图 4
合作 & 交S流1+☞S2=S3
a等²+腰a直²=角c三²角形两直角边

《勾股定理》PPT课件5 (共24张PPT)

《勾股定理》PPT课件5 (共24张PPT)

b
弦 股
勾
我们用另外一种方法来说明勾股定理是正确的 c c c c a a a a b b a c c c c b b a b b
用两种方法表示大正方形的面积:
( a b)
2
b
1 4 ( a b) c 2 2
a
b 对比两种表示方法,你得到勾股定理了吗?
a
例 题
【例】如图,一根旗杆在离地面9米处折裂,旗杆顶部落在离 旗杆底部12米处.旗杆原来有多高?
（约公元1千多年）有个叫商高的人对周
公说，把一根直尺折成直角，两端连接得 一个直角三角形，如果勾是3，股是4，那 么弦等于5.
弦 5
勾
∟
3
人们还发现， 在直角三角形中， 勾是6， 62=36, 勾是5， 股是8， 82=64, 股是12， 弦一定是10； 102=100 弦一定是13， 62+82=102
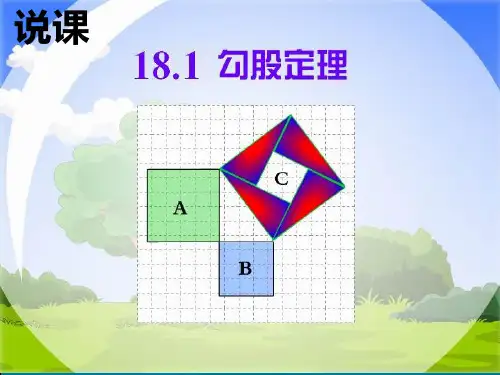
有 9 个小方格，即A的面积 是 9 个单位面积. 正方形B的面积是____ 9 个
单位面积.
正方形C的面积是_____ 18 个单位面积.
（图中每个小方格代表一个单位面积）
（2）（3）
C A B C
S正方形c
1 4 3 3 18 2
（单位面积）
A
B
（图中每个小方格代表一个单位面积）
9米
12米
【解析】设旗杆顶部到折裂处的距离为x米，根据勾股定
理得
9 12 x
2 2
2
x=15, 15+9=24 答：旗杆原来高24米.
跟踪训练
如图,太阳能热水器的支架AB长为 90cm,与AB垂直的BC长120cm.太阳 能真空管AC有多长?

勾股定理说课稿ppt课件

勾股定理说课稿ppt课件

（二）学情分析
八年级学生已初步具有几何图形的 观察，几何证明的理论思维能力。希 望老师预设便于他们进行观察的几何 环境，给他们发表自己见解和表现自 己才华的机会，希望老师满足他们的 创造愿望，让他们实际操作，使他们 获得施展自己创造才能的机会。
580 630
（三）教学方法
数学是一门培养人的思维,发展人的思维的重要学 科,因此,在教学中,要展现获取知识和方法的思维过 程, 针对八年级学生的知识结构和心理特征，本节 课采取引导探索法，由浅入深，由特殊到一般地提 出问题。以导为主,采用设疑的形式，让学生通过观 察、分析、讨论、操作、归纳，理解定理，提高学 生动手操作能力，以及分析问题和解决问题的能力。 5 使学生得到获得新知的成功感受，从而激发学生钻 m 研新知。并利用教具与多媒体进行教学。
2m
活动2、探索勾股定理
探究一（观察特例→发现新知）
{问题一}：在图中你能发现哪些基本图形？ {问题二}：与等腰直角三角形相邻的正方形面积之间 有怎样的关系？ {问题三}：如图，每个小方格的面积为1个单位，你能 写出正方形A、Ｂ、Ｃ的面积吗？ {问题四}：由此你可以得出等腰直角三角形三边存在着一种怎样特殊的数量关 系吗？ 学生在独立探究的基础上观察图片，计算面积，分组交流， 猜想和归纳。 教师参与学生小组活动，指导，倾听学生交流。 设计意图：通过讲传说故事来激发学生学习兴趣，引导学生进入学习状态。 学生会很积极的投入到探索这个问题的实践中。 “问题是思维的起点”，通过层层设问，引导学生发现新知。由正方形的面 积等于边长的平方归纳出：等腰直角三角形两条直角边的平方和等于斜边的平 方。 {问题五}：等腰直角三角形三边具有这样的特殊关系，那么一般的直角三角形 呢？
B
Ｂ
350 A

18.1勾股定理精品PPT课件

18.1勾股定理精品PPT课件

1．观察图1-1（图中每个小方格代表一个单位面积）
正方形A中含有 9 个
小方格，即A的面积是
9 个单位面积．
正方形B的面积是
9 个单位面积．
正方形C的面积是
18 个单位面积．
1 2 3 继续
C A
B
图1-1
你是怎样得到上面的 结果的？与同伴交流
交流．
正方形周边上的 格点数L=12
正方形内部的格 点数N=13
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
§18.1
活动 1
你见过这个图案吗？ 你听说过勾股定理吗？
这就是本届大会 会徽的图案．
这个图案是我国汉代数学 家赵爽在证明勾股定理时用到 的，被称为“赵爽弦图”．
活动 2
相传2500年前，毕达哥拉斯有一次 在朋友家里做客时，发现朋友家用砖铺 成的地面中反映了直角三角形三边的某 种数量关系．
我们也来观察右 图中的地面，看看有 什么发现？
其实勾股定理 中国比西方早 500多年就发现
了哦！
勾股世界
我国是最早了解勾股定理的国家 之一。早在三千多年前，周朝数 学家商高就提出，将一根直尺折 成一个直角，如果勾等于三，股 等于四，那么弦就等于五，即 “勾三、股四、弦五”，它被记 载于我国古代著名的数学著作 《周髀算经》中。
1945年，人们在研究古巴比伦人遗 留下的一块数学泥板时，惊讶地发 现上面竟刻有15组能构成直角三角 形三边的数，其年代远在商高之前。
所以，正方形C的 面积为：
•

勾股定理说课(完整版)PPT课件

勾股定理说课(完整版)PPT课件

教学目标
（1）、知识与技能： 理解勾股定理的两种 证明方法——毕达哥拉斯证法和赵爽的弦图 证法；应用勾股定理解决简单的直角三角形 三边计算问题 （2）、过程与方法：通过对直角三角形三边 关系的猜想验证，经历从特殊到一般的探索 过程，发展合情推理，体会数形结合的思想 （3）、情感态度与价值观：在勾股定理的探 索过程中感受数学文化的内涵，增进数学学 习的信心
2、直角ABC的一条直角边a=10,斜边 c=26，则b=
( 24 )。
３、已知：∠C＝90°，a=6， a：b＝3：4， 求b和c。
c=10 b=8
ac
b
1.说一说本节课我有哪些收获? 2.本节课我还有哪些疑惑?
-
作业
必做题：课本69页第一题。 选做题：收集有关勾股定理的其它 证明方法，下节课展示、交流。
图2
4
9
13
图2
C
A
B
图3
图3
9 25 34
A、B、 C面积 关系
直角三 角形三 边关系
sA+sB=sC
两直角边的平方和 等于斜边的平方
ac
结论
b
直角三角形两直角边的平方和等于斜边的平方．
是不是所有的直角三角形都具有这样的特点呢？ 这就需要我们对一个一般的直角三角形进行证 明．到目前为止，对这个命题的证明方法已有几百 种之多．下面我们就来看一看我国数学家赵爽是怎 样证明这个命题的．
教学重点、难点
重点：探究并理解勾股定理 难点：探索勾股定理的验证方法
教法 分析
平行线的性质是学生对图形性质的第一 次系统研究，对于研究过程和研究方法都 是陌生的，所以学生需要在老师的引导下 类比研究平行线的判定的过程来构建平行 线的性质的研究过程。

勾股定理说课获奖课件(共34张PPT)

勾股定理说课获奖课件(共34张PPT)
学法分析
在教师的组织引导下，学生采用自主探究合作交流的研讨式学习方式,使学生真正
成为学ห้องสมุดไป่ตู้的主人
CONTENTS
04 Part Four 教学过程与设计
01 创设情境
探索新知
06 板书设计及
课堂反思
02
互动新授
05 作业布置
03 分层练习
04 课堂小结
(一)、情境导入
• 2002年世界数学家大会在我国北京召开，会标中央 的图案是一个与“勾股定理”有关的图形，数学家曾 建议用“勾股定理”的图来作为与“外星人”联系的信 号．今天我们就来一同探索勾股定理吧
方法1：补形法(把以斜边为边长的正方形补成各边都 在网格线上的正方形）：
方法2：分割法(把以斜边为边长的正方形分割成易求出
面积的三角形和四边形）：
正方形面积间的关系：SA+SB=SC
猜想:两直角边a、b与斜边c 之间的关系？
两条直角边上的正方形面
A
积之和等于斜边上的正方
a
形的面积．
Bb c C
Sa+Sb=Sc
a2+b2=c2
猜想： 如果直角三角形的两直角边长分别是
a、b，斜边长是c，那么a2+b2=c2。
a2+b2=c2
弦
c
是不是所有的直角三角形都具有这样的特点呢？
股 这就需要我们对一般的直角三角形进行证明．到目
b 前为止，对这个命题的证明方法已有几百种之
┏
勾a
多．下面我们就来看一看我国数学家赵爽是怎样证 明这个命题的．
感谢您的观看 THANKS
勾股定理
x
1 第1,2,3,4,题。
方法1：补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形）：

勾股定理说课稿ppt课件

勾股定理说课稿ppt课件

2.5m
驶向胜利 的彼岸
（五）教学过程
根据学生的认知规律和学习心理，本节课分 六个活动进行学习，为了扩大课堂容量节省时间 提高课堂效率，拟采用多媒体教学。
活动1、了解勾股定理 （创设情境→激发兴趣 ）
2002年在北京召开的第24届国际数学家大会， 2.5m 它是最高水平的全球性数学科学学术会议， 被誉为数学界的“奥运会”。这就是本届大会 会徽的图案（著名的赵爽弦图）。 它象一个 转动的风车，挥舞着手臂，欢迎来自世界各 国的数学家们。 （1）你见过这个图案吗？（2）你听说过“勾股定理”吗？ 5 设计意图：在学生欣赏赵爽弦图的过程中，进行爱国主 5 义教育，可以让他们充分体会到我国古代在数学研究方面取 m m 得的伟大成就，从而激发学生的爱国热情和民族自豪感。激 发学生学习兴趣，自然引出本节课的课题。
2m
活动2、探索勾股定理
探究一（观察特例→发现新知）
{问题一}：在图中你能发现哪些基本图形？ {问题二}：与等腰直角三角形相邻的正方形面积之间 有怎样的关系？ {问题三}：如图，每个小方格的面积为1个单位，你能 写出正方形A、Ｂ、Ｃ的面积吗？ {问题四}：由此你可以得出等腰直角三角形三边存在着一种怎样特殊的数量关 系吗？ 学生在独立探究的基础上观察图片，计算面积，分组交流， 猜想和归纳。 教师参与学生小组活动，指导，倾听学生交流。 设计意图：通过讲传说故事来激发学生学习兴趣，引导学生进入学习状态。 学生会很积极的投入到探索这个问题的实践中。 “问题是思维的起点”，通过层层设问，引导学生发现新知。由正方形的面 积等于边长的平方归纳出：等腰直角三角形两条直角边的平方和等于斜边的平 方。 {问题五}：等腰直角三角形三边具有这样的特殊关系，那么一般的直角三角形 呢？
2

《勾股定理》PPT

《勾股定理》PPT
综合题：3.如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1，求 △ABC的周长．
小贴士
为什么叫勾股定理这个名称呢？ 在中国古代，人们把弯曲成直角的手臂的上半部分称 为“勾”，下半部分称为“股”.我国古代学者把直角三 角形较短的直角边称为“勾”，较长的直角边称为 “股”，斜边称为“弦”.由于命题1反映的正好是直 角三角形三边的关系，所以叫做勾股定理.
勾
股
勾2+股2=弦2 国外又叫毕达哥拉斯定理
当BC为斜边时，如图，BC 42 32 5.
B B
4
3
C 图 A
4
A
3
图
C
归纳 当直角三角形中所给的两条边没有指明是斜边或 直角边时，其中一较长边可能是直角边，也可能是斜 边，这种情况下一定要进行分类讨论，否则容易丢解.
当堂练习
1.下列说法中,正确的是
（ C）
A.已知a,b,c是三角形的三边，则a2+b2=c2
新知应用
例1 如图，在Rt△ABC中， ∠C=90°.
（1）若a=b=5,求c;
B
（2）若a=1,c=2,求b.
a
解：(1)在Rt△ABC中， ∠C=90°
C
c a2 b2 52 52 50 5 2;
c
A
b
(2)在Rt△ABC中， ∠C=90°
b c2 a2 22 12 3.
注意：1.看好哪个角是直角,选择正确的公式来求边长
C
问题2 图中正方形A、B、C所围成的等腰直角三角 形三边之间有什么数量关系？
AB C
S正方形A S正方形B S正方形C
一直角边2 +
另一直角边2 =
斜边2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
感谢阅读！为了方便学习和使用，本文档的内容可以在下载后随意修改，调整和打印。欢迎下载！
汇报人：XXXX 日期：20XX年XX月XX日
7
山阴六中 白晋晓
2020/10/13
1
《勾股定理》的探究是人教版 数学八年级下册第十八章第一节 第一课时的内容。我将从教材分 析、教学目标分析、教法与学法 分析、教学过程分析四个方面对 本节课的教学设计进行说明。
2020/10/13
2
一、教材分析
1、教材的地位和作用
勾股定理在数学学习中有着至关重要的作用。它是
教学难点
用拼图方法、面积法证明 勾股定理。
2020/10/13
5
三、教学与学法
本节课采用探究发现式教学，由浅入 深，由特殊到一般地提出问题，鼓励学生 采用观察分析，自主探索，合作交流的学 习方法，让学生经历数学知识的形成与应 用的过程。
2020/10/13
Байду номын сангаас
6
谢谢您的指导
THANK YOU FOR YOUR GUIDANCE.
决实际问题。
过程与方法
让学生经历用面积法、拼图法探索勾股定理的过程，
体会数形结合的思想，渗透观察、归纳、猜测、验证的数
学方法，体验从特殊到一般的逻辑推理过程。
情感、态度与价值观
通过了解勾股定理的历史，激发学生热爱祖国，热爱祖
国的悠久文化，激励学生发奋学习。
2020/10/13
4
教学重点:
探索和验证勾股定理 。
2、学情分析
勾股定理是学生在已经掌握了直角三角形的有关性
质的基础上进行学习的，学生已经对图形的探索、验证
有了一定的推理能力.
2020/10/13
3
二、教学目标分析
根据本节课的内容和学生的认知特点，我将本节课的教
学目标设置为：
知识与技能：
使学生在探索勾股定理的过程中，掌握直角三角形三
边之间的数量关系。运用勾股定理进行简单的计算，并解
数形结合的代表，是用数学方法来解决几何问题的基础
桥梁。
本节课的主要内容是对勾股定理的探索和验证。它
是直角三角形的一条非常重要的性质，揭示了一个直角
三角形三条边之间的数量关系。在此基础上，让学生利
用勾股定理来解决一些实际问题。在中学数学学习中，
勾股定理也为后面三角函数的学习及一些图形的计算打
下必要的基础。