材料力学(柴国钟、梁利华)第5章答案

材料力学刘德华版课后习题答案word版2.1 试求图示杆件各段的轴力，并画轴力图。

2.2 已知题2.1图中各杆的直径d =20mm ，F =20kN ， q =10kN/m ，l =2m ，求各杆的最大正应力，并用图形表示 正应力沿轴线的变化情况。

答 （1）63.66MPa ，（2）127.32MPa ，（3）63.66MPa ，（4）-95.5MPa ，（5）127.32MPa15kN 15kN 20kN10kN(4)10kN10kN 30kN+---FN 图-+++FFFF20k N 40k N 40k N20k N (2)(1)F N图图NF l(5)qFq l(5)qF +127.32MPa15kN 15kN 20kN10kN(4)31.85MPa+---Fs 图31.85MPa95.5MPa 4m 4mabF题2.4图FF2.8 图示钢杆的横截面积 A=1000mm2，材料的弹性模量E=200GPa ，试求：（1）各段的轴向变形；（2）各段的轴向线应变；（3）杆的总伸长。

解：轴力图如图所示2.10 图示结构中，五根杆的抗拉刚度均为EA ，杆AB 长为l ，ABCD 是正方形。

在小变形条件下，试求两种加载情况下，AB 杆的伸长。

解 （a ）受力分析如图，由C 点平衡可知： F ’AC=F ’CB=0； 由D 点平衡可知： F ’AD=F ’BD=0 再由A 点的平衡：因此（b ）受力分析如图，由C 点平衡可知：-+20kN20kN ⅠⅡⅢ20kN20kN1m 1m 2m12320N 0N 20N N N N F k F k F k ===-11196243339620120010100010020221020010100010N N F l L EA L m F l L m EA ---⨯∆==⨯⨯⨯∆=⨯∆===-⨯⨯⨯⨯4411122244333101010210102L ml mL l L ml mεεε----∆===∆==∆-⨯===-41243100210L m L m L m--∆=∆=∆=-⨯I II III 0.1mm 00.2mm 0.1mm l l l l ∆=∆+∆+∆=+-=-2222AC AD F FF F='=F F (a )ABCD C A F F F F F F F AB AC AD AC ADD F CBF F AB F x AB =0:=F F F ∑AB AB F l Fl L EA EA ∆==C F F AF F AB C DF(b )AF CBF F AB0:0:2x ACBC y oF F F F =''==∑∑再由A 点的平衡：因此2.12 图示结构中，水平刚杆AB 不变形，杆①为钢杆，直径d1=20mm ，弹性模量E1=200GPa ；杆②为铜杆，直径d2=25mm ，弹性模量E2=100GPa 。

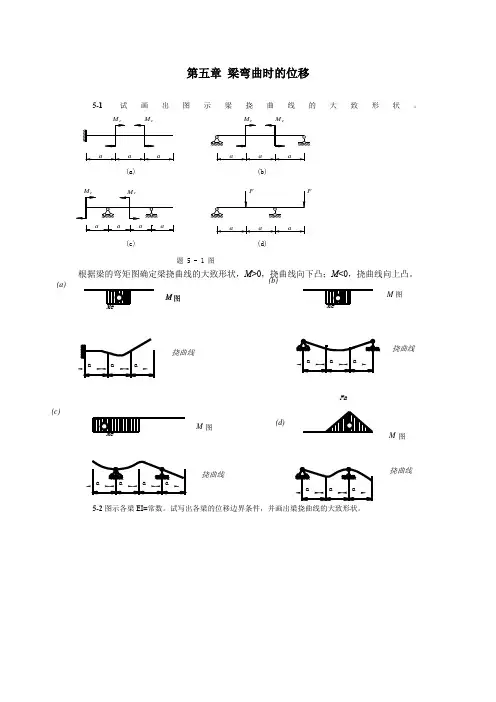
+-++(a)(b)(c)(d)M M M MeMeMeFa图图图M 图挠曲线挠曲线挠曲线挠曲线第五章梁弯曲时的位移5-1试画出图示梁挠曲线的大致形状。

根据梁的弯矩图确定梁挠曲线的大致形状，M >0，挠曲线向下凸；M <0，挠曲线向上凸。

5-2图示各梁EI=常数。

试写出各梁的位移边界条件，并画出梁挠曲线的大致形状。

F(c)题 5 - 1 图(a)(b)(d)++-M 图M 图FL/2m/32m/3FL挠曲线挠曲线(a)(b)设梁的最左端断点为坐标原点，x 轴正方向向右。

则各梁边界条件、弯矩图及梁的挠曲线大致形状如下： (a)(0)0ω=(b)(0)()0L ωω== (c)(0)()0L ωω== (d)(0)(2)0a ωω==(e)()(3)0a a ωω==(f)(0)0ω=(a)(b)qL/4F(d)(c)L(f)(e)题 5 - 2 图+--M 图M 图+qL2/64qL2/8FaFa挠曲线挠曲线(c)(d)+-M 图M 图-2mmFL挠曲线挠曲线(e)(f)5-3试画出图示梁挠曲线的大致形状。

2(a)(b)(c)题 5 - 3 图（3）++--qa2qa/423qa/42qa2/2qa2/2(a)(b)+-m(c)5-4如要使图示结构B端的挠度为零，则长度x应为多少？试画出此时AB梁的挠曲线大致形状。

答：Lx32=解:固定端约束反力如图所示。

则AB梁上距离A端l处的横截面上的弯矩为M（l）=Fl-F（L-x）由挠曲线微分方程得：EIω”=-M（l）=F（L-x）-Fl积分得：EIω’=F（L-x）l-2Fl2+C1;再积分得：EIω=2F（L-x）l2-6Fl3+C1l+C2；由边界条件l=0 ，ω’=0得C1=0；由ω=0得C2=0L题 5 - 4 图题 5 - 5 图刚性杆qBB∴EI ω=2F （L -x ）l 2-6F l 3；由题意知l =L 时，ω=0得x =32L AB 梁挠曲线大致形状：M （l ）=Fl -3F L ；0<l <3L 时，M （l ）<0;3L<l <L 时，M （l ）>05-5图示刚架在端点C 处受集中力F 作用，试求当B 点的铅垂位移为零时La的比值。

5.1 试确定图示梁的危险截面，分别计算图示三种截面上1、2、3点处的正应力。

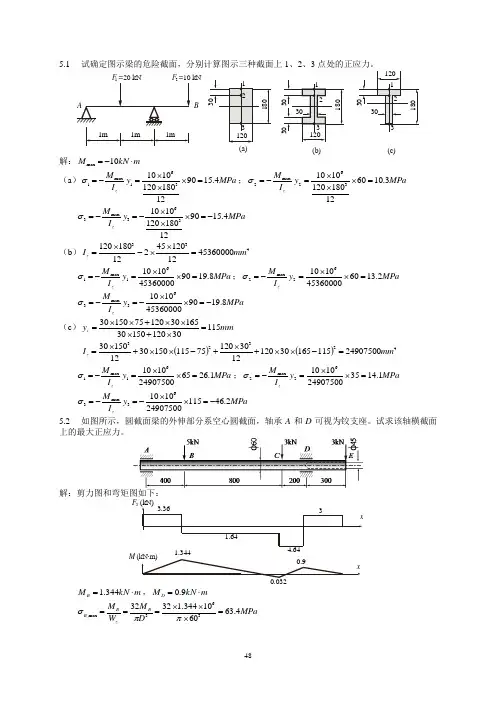
F =20kNF =10kN1m 1m 1m1203BA 122180301120321803030301(a)(b)(c)1203218030301解：m kN M ⋅-=10max（a ）MPa y I M z 4.1590121801201010361max 1=⨯⨯⨯=-=σ；MPa y I M z3.1060121801201010362max 2=⨯⨯⨯=-=σMPa y I M z4.1590121801201010363max 3-=⨯⨯⨯-=-=σ（b ）433453600001212045212180120mm I z =⨯⨯-⨯=MPa y I M z 8.199045360000101061max 1=⨯⨯=-=σ；MPa y I M z 2.136045360000101062max 2=⨯⨯=-=σMPa y I M z 8.199045360000101063max 3-=⨯⨯-=-=σ（c ）mm y c 1153012015030165301207515030=⨯+⨯⨯⨯+⨯⨯=()()423232490750011516530120123012075115150301215030mm I z =-⨯⨯+⨯+-⨯⨯+⨯=MPa y I M z 1.266524907500101061max 1=⨯⨯=-=σ；MPa y I M z 1.143524907500101062max 2=⨯⨯=-=σMPa y I M z 2.4611524907500101063max 3-=⨯⨯-=-=σ5.2 如图所示，圆截面梁的外伸部分系空心圆截面，轴承A 和D 可视为铰支座。

试求该轴横截面上的最大正应力。

解：剪力图和弯矩图如下：3.361.3440.91.644.643F (kN)S xxM (kN m)m kN M B ⋅=344.1，m kN M D ⋅=9.0MPa D M W M B z B B 4.636010344.13232363max,=⨯⨯⨯===ππσ()()MPa D M W M D z D D 1.6275.0160109.03213243643max,=-⨯⨯⨯⨯=-==παπσ 故，MPa 4.63max =σ5.3 图示简支梁受均布载荷作用。

二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d)解：。

2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：返回2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）返回2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此返回2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

试求C点的水平位移和铅垂位移。

解：（1）受力图（a），。

（2）变形协调图（b）因，故=（向下）（向下）为保证，点A移至，由图中几何关系知；返回第三章扭转3-13-23-33-43-53-63-73-83-93-103-113-123-1 一传动轴作匀速转动，转速，轴上装有五个轮子，主动轮Ⅱ输入的功率为60kW，从动轮，Ⅰ，Ⅲ，Ⅳ，Ⅴ依次输出18kW，12kW,22kW和8kW。

二、轴向拉伸和压缩2-1 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d) 解：。

2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：返回2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6) 图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）返回2-7(2-9) 一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11) 受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此返回2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

试求C点的水平位移和铅垂位移。

解：（1）受力图（a），。

（2）变形协调图（b）因，故=（向下）（向下）为保证，点A移至，由图中几何关系知；返回第三章扭转3-13-23-33-43-53-63-73-83-93-103-113-123-1 一传动轴作匀速转动，转速，轴上装有五个轮子，主动轮Ⅱ输入的功率为60kW，从动轮，Ⅰ，Ⅲ，Ⅳ，Ⅴ依次输出18kW，12kW,22kW和8kW。

+-++(a)(b)(c)(d)M M M MeMeMeFa图图图M 图挠曲线挠曲线挠曲线挠曲线第五章梁弯曲时的位移5-1试画出图示梁挠曲线的大致形状。

根据梁的弯矩图确定梁挠曲线的大致形状，M >0，挠曲线向下凸；M <0，挠曲线向上凸。

5-2图示各梁EI=常数。

试写出各梁的位移边界条件，并画出梁挠曲线的大致形状。

F(c)题 5 - 1 图(a)(b)(d)++-M 图M 图FL/2m/32m/3FL挠曲线挠曲线(a)(b)设梁的最左端断点为坐标原点，x 轴正方向向右。

则各梁边界条件、弯矩图及梁的挠曲线大致形状如下： (a)(0)0ω=(b)(0)()0L ωω== (c)(0)()0L ωω== (d)(0)(2)0a ωω==(e)()(3)0a a ωω==(f)(0)0ω=(a)(b)qL/4F(d)(c)L(f)(e)题 5 - 2 图+--M 图M 图+qL2/64qL2/8FaFa挠曲线挠曲线(c)(d)+-M 图M 图-2mmFL挠曲线挠曲线(e)(f)5-3试画出图示梁挠曲线的大致形状。

2(a)(b)(c)题 5 - 3 图（3）++--qa2qa/423qa/42qa2/2qa2/2(a)(b)+-m(c)5-4如要使图示结构B端的挠度为零，则长度x应为多少？试画出此时AB梁的挠曲线大致形状。

答：Lx32=解:固定端约束反力如图所示。

则AB梁上距离A端l处的横截面上的弯矩为M（l）=Fl-F（L-x）由挠曲线微分方程得：EIω”=-M（l）=F（L-x）-Fl积分得：EIω’=F（L-x）l-2Fl2+C1;再积分得：EIω=2F（L-x）l2-6Fl3+C1l+C2；由边界条件l=0 ，ω’=0得C1=0；由ω=0得C2=0L题 5 - 4 图题 5 - 5 图刚性杆qBB∴EI ω=2F （L -x ）l 2-6F l 3；由题意知l =L 时，ω=0得x =32L AB 梁挠曲线大致形状：M （l ）=Fl -3F L ；0<l <3L 时，M （l ）<0;3L<l <L 时，M （l ）>05-5图示刚架在端点C 处受集中力F 作用，试求当B 点的铅垂位移为零时La的比值。

第5章作业答案5-1解：1-1截面弯矩 21111000160011300N m 2M −=−×−××=−i A 点应力 3113130010(55)122.54MPa 100150A A z M y I σ−−××−×===× （拉应力） B 点应力 311313001035121.62MPa 100150B B z M y I σ−−×××===−× （压应力） 5-4解:（1）求支座反力由 0=ΣA m ，0212=×+×−×a P a P a R B 解得 6=B R kN由 0=ΣY ，012=−++−A B R P P R 解得 22=A R kN（2）作弯矩图8.4−=×−=a P M A kN•m6.3=×=a R M B C kN•m(3)求最大拉压应力由弯矩图可知，截面A 的上边缘及截面C 的下边缘受拉；截面A 的下边缘及截面C 的上边缘受压。

虽然C A M M >，但 12y y <，所以只有分别计算此二截面的拉应力，才能判断出最大拉应力所对应的截面；截面A 下边缘的压应力最大。

截面A 上边缘处36101033.51040108.4126332=×××××==−−z A t I y M σMPa 截面C 下边缘处54101033.51080106.3126331=×××××==−−z C t I y M σMPa 比较可知在截面C 下边缘处产生最大拉应力，其值为54max =t σMPa 截面A 下边缘处72101033.51080108.4126331max=×××××==−−z A c I y M σMPa5-5解：1)计算最大弯矩：33max 2200N 239510m= 5.26910N m M −=−××−×⋅ 2)确定最大正应力：()()()max max max33344666mm0611108mm 5268N m π2π10810m 212106113232247110Pa=24.71MPaM M D W ασα−==⋅===××−×−=×....5-7解：1)计算截面弯矩m-m 截面弯矩 m-m 20kN m M =in-n 截面弯矩 n-n 2015325kN m M =−×=−i 2)计算各点应力 m-m 截面：A 点 62201067.4MPa 180300m m A z M W σ−××=−=−=−× （压应力） B 点 632010100124.9MPa 180300m m B B z M y I σ−×××===×（拉应力） C 点 6320100120180300m m C C z M y I σ−×××===× D 点 62201067.4MPa 180300m m D z M W σ−××=−==× （拉应力） n-n 截面：A 点 62251069.3MPa 180300n n A z M W σ−××===× （拉应力） B 点 632510100126.2MPa 180300n n B B z M y I σ−−×××===−×（压应力） C 点0C σ=D 点 62251069.3MPa 180300n n D z M W σ−××=−=−=−× （压应力）5-85-11 答案见课件5-16 答案见课件5-175-19解：1）画弯矩图C 截面左侧弯矩为-30 kN ·m ，右侧弯矩为40 kN ·m ，左右两截面均可能为危险截面。

第五章弯曲应力5-1 直径为d的金属丝，环绕在直径为D的轮缘上。

试求金属丝内的最大正应变与最大正应力。

已知材料的弹性模量为E。

解：5-2 图示直径为d的圆木，现需从中切取一矩形截面梁。

试问：(1) 如欲使所切矩形梁的弯曲强度最高，h和b应分别为何值；(2) 如欲使所切矩形梁的弯曲刚度最高，h和b应分别为何值；解：(1) 欲使梁的弯曲强度最高，只要抗弯截面系数取极大值，为此令(2) 欲使梁的弯曲刚度最高，只要惯性矩取极大值，为此令5-3 图示简支梁，由№18工字钢制成，在外载荷作用下，测得横截面A 底边的纵向正应变ε=3.0×10-4，试计算梁内的最大弯曲正应力。

已知钢的弹性模量E =200GPa ，a =1m 。

解：梁的剪力图及弯矩图如图所示，从弯矩图可见：5-4 No.20a 工字钢梁的支承和受力情况如图所示。

若[]MPa 160=σ，试求许可载荷F 。

5-5 图示结构中，AB 梁和CD 梁的矩形截面宽度均为b 。

如已知AB 梁高为1h ，CD 梁高为2h 。

欲使AB 梁CD 梁的最大弯曲正应力相等，则二梁的跨度1l 和2l 之间应满足什么样的关系？若材料的许用应力为[σ]，此时许用载荷F 为多大？5-6 某吊钩横轴，受到载荷kN 130F =作用，尺寸如图所示。

已知mm 300=l ，mm 110h =，mm 160b =，mm 75d 0=，材料的[]MPa 100=σ，试校核该轴的强度。

5-7 矩形截面梁AB，以固定铰支座A及拉杆CD支承，C点可视为铰支，有关尺寸如图所示。

设拉杆及横梁的[]MPaσ，试求作用于梁B端的许可载荷F。

=1605-8 图示槽形截面铸铁梁，F=10kN，M e=70kN·m，许用拉应力[σt]=35MPa，许用压应力[σc]=120MPa。

试校核梁的强度。

解：先求形心坐标，将图示截面看成一大矩形减去一小矩形惯性矩弯矩图如图所示，C截面的左、右截面为危险截面。

5-1构件受力如图5-26所示。

试：(1)确定危险点的位置；(2)用单元体表示危险点的应力状态（即用纵横截面截取危险点的单元体，并画出应力）。

题5-1图解：a) 1) 危险点的位置：每点受力情况相同，均为危险点；2）用单元体表示的危险点的应力状态见下图。

b) 1) 危险点的位置：外力扭矩3T与2T作用面之间的轴段上表面各点；2）应力状态见下图。

c) 1) 危险点：A点，即杆件最左端截面上最上面或最下面的点；2）应力状态见下图。

d) 1）危险点：杆件表面上各点；2）应力状态见下图。

5-2试写出图5-27所示单元体主应力σ1、σ2和σ3的值，并指出属于哪一种应力状态（应力单位为MPa）。

10题5-2图AAT（a）（c）（d）364dFlπτ=a) b) c) d)a) b) c)解： a) 1σ=50 MPa, 2σ=3σ=0,属于单向应力状态b) 1σ=40 MPa, 2σ=0, 3σ=－30 MPa ，属于二向应力状态 c) 1σ=20 MPa, 2σ=10 MPa, 3σ=－30 MPa ，属于三向应力状态5-3已知一点的应力状态如图5-28所示（应力单位为MPa ）。

试用解析法求指定斜截面上的正应力和切应力。

题5-3图解：a) 取水平轴为x 轴，则根据正负号规定可知： x σ=50MPa , y σ=30MPa , x τ=0, α=－30 带入式（5-3），（5-4）得 ατασσσσσα2sin 2cos 22x yx yx --++==45MPaατασστα2cos 2sin 2x yx +-== -8.66MPab) 取水平轴为x 轴，根据正负号规定：x σ= -40MPa , y σ=0 , x τ=20 MPa , α=120带入公式，得：240sin 20240cos 20402040---++-=ασ=7.32MPa x τ= 240cos 20240sin 2040+--=7.32MPac) 取水平轴为x 轴，则x σ= -10MPa , y σ=40MPa , x τ= -30MPa,α=30代入公式得：60sin )30(60cos 2401024010----++-=ασ=28.48MPa x τ= 60cos 3060sin 24010---=-36.65MPaa)b)c)5-4已知一点的应力状态如图5-29所示（应力状态为MPa ）。

材料力学课后答案材料力学是研究材料内部力学性质和行为的学科，它是材料科学与工程学的重要基础课程之一。

通过学习材料力学，我们可以了解材料的力学性能和行为，为材料的设计、加工和应用提供理论基础和指导。

在课堂学习之外，课后习题是巩固知识、提高能力的重要途径。

下面是一些材料力学课后习题的答案，希望能对大家的学习有所帮助。

1. 什么是应力？应变？它们之间的关系是什么？答，应力是单位面积上的力，通常用σ表示，其公式为σ=F/A，其中F为作用在物体上的力，A为物体的受力面积。

应变是物体单位长度的形变，通常用ε表示，其公式为ε=ΔL/L0，其中ΔL为长度变化量，L0为原始长度。

应力和应变之间的关系由杨氏模量E来描述，公式为σ=Eε。

2. 什么是弹性模量？它有哪些类型？答，弹性模量是描述材料在弹性阶段的刚度和变形能力的物理量。

常见的弹性模量包括杨氏模量、剪切模量、泊松比等。

3. 什么是拉伸、压缩、剪切？答，拉伸是指物体在外力作用下沿着其长度方向发生的形变；压缩是指物体在外力作用下沿着其长度方向发生的缩短形变；剪切是指物体在外力作用下沿着其平面内部发生的相对位移形变。

4. 什么是胶性变形？塑性变形？答，胶性变形是指材料在受力作用下发生的可逆形变，即在去除外力后，材料可以恢复到原来的形状；塑性变形是指材料在受力作用下发生的不可逆形变，即在去除外力后，材料无法完全恢复到原来的形状。

5. 什么是材料的疲劳破坏？有哪些影响因素？答，材料的疲劳破坏是指在交变应力作用下，材料在循环载荷下发生的破坏。

影响因素包括应力幅值、载荷次数、材料的强度和韧性等。

以上是对材料力学课后习题的部分答案，希望能够帮助大家更好地理解和掌握材料力学的知识。

在学习过程中，要多做习题、多思考、多讨论，相信通过努力，一定能够取得好成绩。