变中找不变

在变中寻找不变作文800英文回答：In the ever-changing tapestry of life, finding constants can serve as an anchor amidst the chaos. Like a beacon in a tempestuous sea, they provide a sense of stability and orientation.Throughout history, great minds have grappled with the notion of permanence amidst change. Heraclitus, the enigmatic Greek philosopher, famously declared, "Everything flows." Yet, even in this relentless flux, he recognized the enduring nature of change itself. Centuries later, the Roman poet Ovid echoed this sentiment, writing, "Everything changes, yet everything remains the same."In the realm of science, the laws of nature and the fundamental forces of the universe stand as steadfast principles that govern the seemingly chaotic dance of particles and energy. From the motion of celestial bodiesto the interactions of subatomic particles, these laws provide an unwavering framework that transcends the ephemeral nature of individual events.In the human experience, too, there are constants that endure despite the passage of time. Love, compassion, and the indomitable spirit of resilience have anchored countless hearts across generations. These qualities, deeply rooted in our humanity, serve as a reminder of our shared experiences and the profound connections that bind us.Our own bodies, subject to the ravages of time, undergo constant renewal and regeneration. Cells divide and replenish, tissues repair themselves, and the intricate machinery of our being continues to function with remarkable resilience. While the superficial aspects of our bodies may change, the underlying processes that sustain life remain remarkably similar.Likewise, in the realm of culture and society, certain traditions, values, and beliefs have proven remarkablydurable. They shape our identities, guide our interactions, and provide a sense of continuity in a rapidly evolving world. From the rituals of religious observance to the shared narratives of our collective past, these cultural touchstones offer a sense of belonging and stability.In the face of adversity, whether personal or global,it is often the search for constancy that gives us hope. We seek refuge in familiar routines, draw strength from cherished relationships, and find solace in the unwavering rhythms of nature. By embracing the immutable, we find the fortitude to navigate the unpredictable currents of life.中文回答：在变幻莫测的人生织锦中，寻找不变的事物可以成为一片混乱中的锚点。

（２）如图 ２，连接 ＡＤ，与 （１）相比较 ，少 Ｊ，条件 ＡＢ＝ＡＣ，故不能 运用 “三线 合一 ”，但 由条件 “Ｄ
为 ＢＣ的 中点 ”仍 可得 ：ＳＡ ４ＢＤ￣Ｓ 所 以 １ ＡＢ·
ＤＭ＝ ＡＣ‘ＤＮ，所以 ＝
＝ １ ，
：（￣
ＡＤＥＭ
一△ＤＦⅣ的基础上，得：丽ＤＥ＝ ＝去。
这样 的试题具有从特殊 到一般 ．不断深入 的特 点 ，由问题 （１）到 问题 （３）归纳 起来 ，其 中 变 化 的有 ：将 等腰 变 成 非 等腰 、将 点 Ｄ为 ＢＣ 的 中点 变为 非 中点 ，问题 逐 步一 般化 。但解 决 问题 的思路 有两个不 变 ：① ＡＡＢＤ与 ＡＡＣＤ 面积关 系转化 为数量 关系的方法不变 ；②证 明 ＡＤＥＭ￣＂ＡＤＦＮ的方 法没 有改 变 。抓住 了这 两点 ，即可对线段之间 的关系进 行转化 。
并说 明理 由 。（３）如 图 ３，若 ：。，且 ＝６，
一 ” ， 故连接 ＡＤ得 ＡＤ平 分ＬＢＡＣ。从 结论上分 析 ，需要构 造两个三 角形 全等进 行证明 ，若过 点 Ｄ分别作 ＤＭ＿ＬＡＢ，ＤＮ＆ＡＣ，根据 “角平 分线 定理”可得 ＤＭ＝ＤＮ。
也可 根据 Ｄ为 ＢＣ的 中点得 ：ＳＡＡＢＤ＝ｓ 再得 ：ＤＭ＝ＤＮ，结 合四 边形 ＡＭＤＮ中 ，Ｚ．ＭＤＮ＋ ／＿ＢＡＣ＝１８０。和 条件 中 ＺＥＤＦ＋Ｚ＿ＢＡＣ＝Ｉ８０。，得 Ｚ＿ＭＤＮ＝ＬＥＤＦ，同 时 减 去 公 共 角 ＺＭＤＦ后 ， 得 到 Ｚ￣ＤＭ＝／ＦＤＮ，从 而运 用 全 等 三 角形 证 得 结 论 。
例题 在 ＡＡＢＣ中，点Ｄ为ＢＣ边上的任意 一 点 。以 点 Ｄ为 顶 点 的 ＤＦ的 两 边 分 别 与 边 ＡＢ，ＡＣ交于点 Ｅ，Ｆ，且 Ｚ．ＥＤＦ与 互补 。

浅谈六年级数学教学中“变中有不变”思想的渗透发布时间：2021-11-16T07:52:28.282Z 来源：《教育学》2021年8月总第257期作者：王盼桃[导读] 老师通过实验活动探究几个大小不同的圆的周长与直径来探索圆周率。

陕西省渭南市临渭区北塘实验小学714000摘要：小学阶段，在学习数学或用数学解决问题的过程中会面对千变万化的对象，在这些变化中找到不变的性质和规律，发现数学的本质，这就是“变中有不变”的思想。

所谓“万变不离其宗”，恰当通俗地概括了这一思想。

小学数学虽然是数学中最基础、最简单的部分，从容量和难度来看都不算大，但对于小学生来说确实是有难度的，这是由小学生的认知特点决定的。

在课堂教学中，如果能够多体现“变中有不变”的思想，将有利于更好地认识数学的本质和解决问题。

关键词：变中有不变渗透本质一、在探索抽象公式的过程中渗透“变中有不变”思想1.圆的周长公式的探索中渗透“ 变中有不变”思想。

六年级上册第一单元《圆》中圆的周长，在这个公式的探讨过程中，通过学生动手操作用绳测法或滚动法把圆的周长化曲为直，然后提出圆的周长与它的直径长短有关系。

老师通过实验活动探究几个大小不同的圆的周长与直径来探索圆周率。

为了找到其中不变的或者有规律性的变化，学生会用这两组数据中相对应的两个数相除。

通过小组一系列的计算探究出圆周率是一个圆周长除以它的直径所得的商，是一个固定不变的数。

通过教师的指引让学生知道圆的周长随着它的直径变化而变化，而圆周长(C)与它的直径(d)所得商却是一个不变的固定的数，它就是圆周率(π)。

圆的周长和直径是变化的，而它们两数之间对应的商却是不变的，理解圆的周长计算公式为C=πd，让学生在“变中有不变”，领悟圆周率是一个固定的数。

2.圆柱的体积公式的探索中渗透“变中有不变”思想方法。

在圆柱体积公式的探究过程中，通常把圆柱转化为近似长方体，再推导出圆柱体积的计算公式。

在这一推导过程中很多老师都强调了“转化”的数学思想方法，其实还有“变中有不变”的数学思想。

变化中寻不变探究中求推广
变与不变是永恒的话题。

由不变“到”变，是生活中的常态，也是进步的源泉。

变与不变的矛盾性实际是一种矛盾的博弈，变的多少有着明确的范围和度量，在探究中求推广的可能性也便展露无余。

变与不变实质上有着印象深刻的对立性，变迁引发深刻变化，而不变则拒绝突变，稳定起来像一副张力背后存在的另一侧，让我们有机会去探询这种对比变化之间的动态。

有了变与不变，发展才能有更多可能性，不变可以稳定某一状态，守护它、保护它不受外界影响，变则可以向更高境界靠拢，创造出新的可能性。

在发展的种种过程中，克服不变的状态，通过不断的变与不变的平衡，推动发展的有机分子在变与不变之间动态结合，推动发展变得更加健康。

万物来去，唯有变与不变的对立定律存在相对的稳定，这才是我们永恒的发展动力，才能在一波波变化中寻求更加深入的理解，更加全面而深刻的认识。

在变与不变之间，探究发展源头，从其中求得推广，是努力追求着平衡发展的理想目标。

———自编教材《转化单位“1”》教学例谈文|钱定娟蒋明玉（特级教师）【教学过程】一、回忆策略，唤醒“转化”师：同学们，我们学习了很多解决问题的策略：从条件想起、从问题想起、列表策略、画图策略、列举策略、转化策略、假设策略（课件相应演示每个例题图）。

五年级下学期学习的转化策略，你还记得吗？生：通过平移、旋转等方法，把不规则图形转化成规则图形。

师：图形中有转化，计算中也有转化：12+14+18+116。

生：1-116。

师：不直接相加，而是用1减去空白部分，把繁琐的分数连加转化为相对简单的分数减法。

有人说，数学学习就是不断学会转化，把复杂的转化为简单的，把未知的转化为已知的，把陌生的转化为熟悉的。

【设计意图：小学从三年级起学了一系列的数学思想方法以及解决问题的策略，配合相应例题图一一呈现，唤起学生的回忆，聚焦“转化”策略，再一次感受“转化”的魅力，也为下文的“转化”埋下伏笔。

】二、例题教学，凸显“转化”1.转化单位“1”，已知量作单位“1”。

出示：星河小学美术组男生人数占总人数的25。

已知女生有21人，男生有多少人？师：谁来读题？关系句是男生人数占总人数的25，表示数量间有怎样的关系？你还能想到什么？生：总人数平均分成5份，男生有这样的2份。

生：男生2份，女生3份，还可以画个图，让数量关系变得更加清晰。

师：想法真不错！（展示学生画的线段图）更清楚地看出男生人数是2份，女生人数是3份。

师：你会解答这一题吗？比一比谁的解法更简便。

生1：21÷（1-25）×25先求出总人数是多少人，男生占总人数的25，再求总人数的25是多少人。

生2：5-2=3，女生人数3份，女生21人，先求出1份多少人，再求男生2份多少人。

生3：直接用21×23就可以求出男生有多少人了。

师：21×23，23是表示谁是谁的23？生：男生人数是女生人数的23。

师：题目中原来是以“总人数”作单位“1”，现在他把谁作单位“1”了？60Copyright©博看网. All Rights Reserved.生：女生人数作单位“1”。

2023年高考语文作文猜题及范文分析：在变局中寻“变”与“不变”
之道
阅读下面的材料，根据要求写作。

宋代苏轼在《赤壁赋》中说：“盖将自其变者而观之，则天地曾不能以一瞬；自其不变者而观之，则物与我皆无尽也！”
现代的我们常常说，变则通，通则达，在竞争激烈的今天，我们若不想被淘汰，就要时刻站在时代的前沿，我们要懂得这样一个道理一这个世界上唯一不变的就是变化。

请你认真阅读上面的材料，结合现实生活，以“变与不变”为主题写一篇文章，可以侧重于“变”或“不变”，也可重点论述两者的关系。

要求：选准角度，确定立意，明确文体，自拟标题；不要套作，不得抄袭；不得泄露个人信息；不少于800字。

【分析】本题考查学生的写作能力。

审题：
这是一道引语式材料作文题。

材料第一段引用了苏轼在《赤壁赋》中“盖将自其变者而观之，则天地曾不能以一瞬……”的语句，意思是从事物易变的一面看来，天地间万事万物时刻在变动，连一眨眼的工夫都不停止；从事物不变的一面看，那么客观事物与我们人类都是无穷无尽，永远长存的。

前者表明“变”是物质运动的规律。

后者强调的则是生生不息的相对的“变”。

第二段则结合当今时代让学生思考如何应对这个快速变化的世界，同
第1页共6页。

在变化中找不变高中物理“力的平衡”一章里“力的分析”是大部分学生学习的障碍，许多学生对“力的变化问题”更是感觉力不从心。

笔者从事高中物理教学多年来，逐渐摸索出了一些关于“力的变化”问题的解决方法、思路，总结为一句话是“在变化中找不变”。

在多年的教学实践应用中，发现使用这种方法使学生接受该部分知识的速度大大加快，解题能力也相应提高，课堂反应良好。

“力的变化”问题的分析方法比较多，有平行四边形法、三角形法、相似形法等。

若涉及求极值、可能值问题，三角形法和平行四边形法比较易于确定极值状态。

本文拟对”力的变化”问题进行类型、方法的分类，为解决“力的变化”这类问题提供一种思维方法。

问题出现的语言特征：1.力如何变化、力的变化情况。

（显性表达）2.力的最大值或最小值、力的大小可能值。

（隐形表达）也就是说，一旦我们在读题时遇到上述的语言表述时，就可以把该题归结为“力的变化”题型，就可以采用以下的方法进行解题。

一、力的变化问题解决此类问题的方法首先是在变化中找到“不变”的因素，如不变力的大小、方向，并画出不变力的大小、方向的示意图。

1.若能找到一个不变的力和一个不变方向的力，则运用“平行四边形法则”。

平行四边形法：（1）首先作出物体所受不变力的示意图（大小或方向不变的力）。

（2）作出两个变力的合力（与不变力等大反向，相当于平行四边形的对角线）。

（3）过作用点作出方向不变力的作用线（相当于平行四边形的一条边的方向）。

（4）再过合力（相当于平行四边形的对角线）的顶点作出已知方向的力的平行线（这是关键一步），这样就构成了平行四边形的一条对角线和一对对边。

（5）运用平行四边形法则，过合力的始端作出方向变化的力的可能作用线，构成平行四边形，这样两条对边的长度变化即为两个变力的大小或方向的变化趋势。

例题如下：例1.如图1所示，将足球用网兜挂在光滑的墙壁上，设绳对球的拉力为f，墙壁对球的支持力为fn，当细绳长度变短时，试分析力f、fn的变化情况。

平行四边形“生长”出了一系列特殊四边 形,在“生长”的过程中，出现了一些较复杂的 问题。

同学们只要仔细观察、善于发现，在 “变”的现象中抓住“不变'的本质，便可以迅速 抓住解题的突破口。

下面举几例，请同学们一 起来体会其中的奥妙。

例1 如图1 ,在矩形中，已知/10= S,AB=6,P 是AD 上任意一点、，PE 丄BD 于E, PF1AC 于 F,求PE+PF 的值。

【解析】连接0P ,由矩形性质推出AC=BD , OA=OC, OB=OD ,由勾股定理求出4C 和BD 的 长,求出矩形4BCD 的面积，进而得到/\AOD 的 面积。

根据三角形的面积公式即可求出PE+ PF 的值是警。

【点评】初看此题，点P 的位置不确定,PE 、 PF 的长度随之不确定，似乎找不到突破口。

但同学们只要结合已知条件细心观察,就可以 由“在‘点P 位置变化的过程中’矩形ABCD 的 面积不变”推导出“ /\AOD 的面积不变”，这是 解此题的关键。

本题主要考查了矩形的性质、 勾股定理、三角形的面积等知识点。

例2 如图2,在口ABCD 中，作Z.4BC. Z.BCD 的平分线BE 、CF 分别交AD 于点E 、F,若 .4B=8, EF= 1,求 CJABCD 的周长。

［解析】先根据题意补全图形,再根据平行初学习•策略方法“变”中找“不变”朱月红（特级教师）四边形、等腰三角形的性质求出AD 的长即可 求出周长。

答案:50、46。

【点评】本题考查同学们的基本功——平 行四边形具有易变性，体现了思维的灵活性。

作图时要从两方面考虑:BE 、CF 的交点在平行 四边形ABCD 内还是外（也可以思考点E 在点F 的左还是右）。

此题与例1不一样，貌似不变 的图形背后却蕴含着变化（实质是分类讨论）。

有了上面两题的解题经验,下面这道题同学们驱来就轻松了。

例3如图3,在边长为4的正方形ABCD 中，E 是/W 边上的一点，且AE=3,点Q 为对角 线AC 上的动点，求△ BEQ 周长的最小值。

浅谈“变中抓不变”的思想在分数应用题中的应用作者：赵晓舂来源：《新一代》2019年第16期摘要：在学习小学数学中“变中抓不变”的思想是一种常见的重要解题思路，在本文中笔者通过举例来说明应用“变中抓不变”的数学思想化难为易，巧妙地解决一些分数应用题。

关键词：小学数学;分数应用题;变中抓不变数学是一门比较抽象又很贴近现实生活的学科，对学生的逻辑思维能力要求较高。

对于小学生而言，他们分析问题、理解问题的能力较弱，在学习解答数学中的分数应用題时常常感到困难重重，特别是某些应用题中数量关系变化繁多，似乎很难辨别清楚其内在联系。

但是，万变不离其宗，只要我们以不变应万变，在多种数量的变化中找出起关键作用的不变量，就会得到很巧妙的解法，使看上去繁琐的、觉得很难的问题，变的明朗化、简单化，从而也培养了学生解题的灵活性。

一、抓住部分量不变进行解题这类应用题的特点是：两个量中的一个量发生了变化，而另一个量不变，解题时可以把这个不变的量作为解题突破口，寻找解题方法。

【例题1】六（一）班原有学生56人，其中男生占，后来又转进女生若干人，这时女生占总人数的，问：新转来女生多少人？【分析】由条件“又转进女生若干人”可知，女生人数变了，那么，六（一）班的总人数也变了。

“ ”和“ ”虽然都是以总人数为单位“1”的量，但这两个单位“1”的量是不同的。

“ ”是以未转新生前六（一）班的总人数为单位“1”的量，而“ ”是以转来新生后六（一）班的总人数为单位“1”的量。

两个单位“1”的量不同，所以不能直接相加减。

虽然总人数发生了变化，但其中男生人数始终没有变。

如果我们抓住这个不变量解题，问题就能解答了。

【解答】六（一）班男生人数是：56× =32（人），新转来女生若干人后六（一）班的总人数是：32÷（1- ）=60（人），新转来女生人数是：60-56=4（人）。

【例题2】小军原有的钱数是小明的，小军用去100元后，这时小军的钱数是两人总钱数的。

在变化中寻找不变——“分数除以整数”教学新思考新课程标准告诉我们：动手实践、自主探索、合作交流是学生学习数学的重要方式，加强实践操作是培养学生创新学习能力的重要措施。

教师们在新课程标准理念的指引下，逐渐一改以往的“满堂灌”或“一言堂”式教学，都比较注重创设各种情境氛围，重视学生的自主探究学习。

我以“新课标”精神为指导，用活用好教材，让学生经历学习过程，充分体验数学学习，感受成功的喜悦。

“分数除以整数”是苏教版六年级上册的教学内容。

在课堂教学中，我对教材作了灵活的处理，这样为学生提供了更宽阔的探索空间，更有利于体现学生的主体地位，促进学生主动发展。

片段：……原例题师：根据题意要求，独立思考完成。

请学生上台来在图上画出每个小朋友分别喝的部分。

（设计意图：有意识地直观渗透：每人喝的部分其实就是45升果汁的一半）生：45 ÷2＝4÷25 =25（升） 师：同学们的速度真快，那么根据你们画的图与解答，谁能知道每个小朋友喝的部分与“45升果汁”这个总量存在什么联系 学生争先恐后举手，得到结论：每个小朋友喝的部分正好是“45升果汁”的一半。

（板书结论）（其实图画好后一眼就能看出来，这个问题的设计意图是有意识地提醒学生结果与总量之间存在联系，以便于学生联系分数乘法的知识）第一次改例题：师：真不错，现在呀老师再考考你们，看题，把果汁总量“45”升改成 “25”升，其他要求不变。

该如何做呢？动脑筋思考解答。

生： 25 ÷2＝15（升） 师：同学们今天解题的成功率真高！谁能根据图用语言说说？（呈现学生的画图）生：从图上可以看出25升果汁平均分给2个小朋友后每人得到的是15升（学生们一脸的自豪，因为学生自认为太简单了） 师：（适时指图）这个结果也正好是25升果汁的？生跟道：一半。

（板书：每个小朋友喝的部分正好是“25升果汁”的一半） 第二次改例题：师：老师再把数字变一变，你们还能做正确吗？生：（齐答）能。

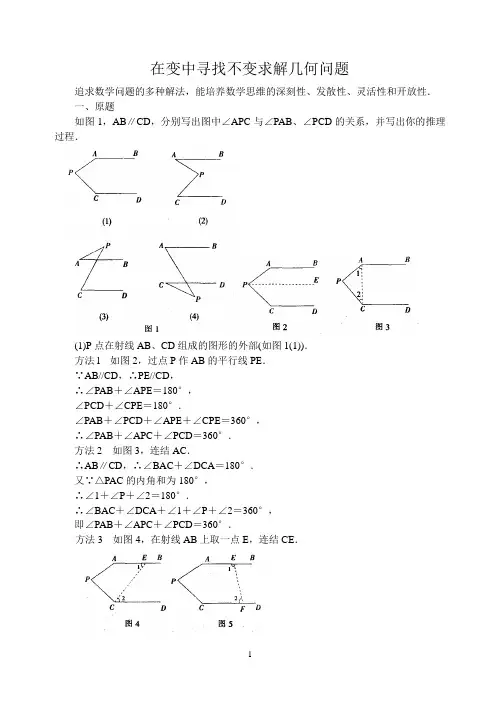
在变中寻找不变求解几何问题追求数学问题的多种解法，能培养数学思维的深刻性、发散性、灵活性和开放性．一、原题如图1，AB∥CD，分别写出图中∠APC与∠PAB、∠PCD的关系，并写出你的推理过程．(1)P点在射线AB、CD组成的图形的外部(如图1(1))．方法l 如图2，过点P作AB的平行线PE．∵AB//CD，∴PE//CD，∴∠PAB＋∠APE＝180°，∠PCD＋∠CPE＝180°．∠PAB＋∠PCD＋∠APE＋∠CPE＝360°，∴∠PAB＋∠APC＋∠PCD＝360°．方法2 如图3，连结AC．∴AB∥CD，∴∠BAC＋∠DCA＝180°．又∵△PAC的内角和为180°，∴∠1＋∠P＋∠2＝180°．∴∠BAC＋∠DCA＋∠1＋∠P＋∠2＝360°，即∠PAB＋∠APC＋∠PCD＝360°．方法3 如图4，在射线AB上取一点E，连结CE．∵四边形APCE的内角和为180°，∴∠1＋∠A＋∠P＋∠PCE＝360°．又∵AB∥CD，∴∠1＝∠2，∴∠2＋∠A＋∠P＋∠PCE＝360°，即∠PAB＋∠APC＋∠PCD＝360°．方法4 如图5，分别在射线AB、CD上任取一点E、F，连结EF．∵五边形APCE的内角和为540°，∴∠1＋∠A＋∠P＋∠C＋∠2＝540°．又∵AB∥CD，∴∠1＋∠2＝180°，∴∠A＋∠P＋∠C＝360°，即∠PAB＋∠APC＋∠PCD＝360°．方法5 如图6，延长CP、BA交于点E∵∠BAP是APE的外角，∴∠BAP＝∠1＋∠2．又∵AB∥CD，∴∠1＋∠C＝180°，∠2＋∠3＝180°．∴∠1＋∠2＋∠3＋∠C＝360°，即∠PAB＋∠APC＋∠PCD＝360°．(2)点P在射线AB、CD组成的图形的内部(如图1(2))．方法1 如图7，过P点作EF∥AB，则∠PAB＝∠APE．又∵AB//CD，∴EF//CD、∴∠PCD＝∠EPC．∴∠APC＝∠PAB＋∠PCD．方法2 如图8，延长CP交AB于点H，则∠PCD＝∠CHA，∴APC＝∠PAB＋∠AHP＝∠PAB＋∠PCD．方法3 如图9，连结AC，则∠APC＋(∠PAC＋∠PCA)＝180°．又∵(∠PAC＋∠PCA)＋(∠PAB＋∠PCD)＝180°，∴∠APC＝∠PAB＋∠PCD．方法4 如图10，分别延长AP、CP，交CD、AB于F、E两点，∴∠APC＝∠EPD．∵AB∥CD，∴∠AEC＝∠PCD．则∠EPD＝∠PAB＋∠AEC＝∠PAB＋∠PCD．∴∠APC＝∠PAB＋∠PCD．方法5 如图11，过点P作PE⊥AB，延长EP交CD于点F，则EF⊥CD．∠APE＋∠PAB＋∠AEP＝180°，∠CPF＋∠PCD＋∠PFC＝180°．∵∠AEP＝90°，∠PFC＝90°，∴(∠APE＋∠CPF)＋(∠PAB＋∠PCD)＝180°．又∵(∠APE＋∠CPF)＋∠APC＝180°，∴∠APC＝∠PAB＋∠PCD．当然，本题的解法还有很多，聪明的你能否再找出几种呢？仿照思路可以解决图1(3)和图1(4)．点评无论点P的位置如何发生改变，都可以运用平行线的性质或内角和、外角的性质来找出各个角之间的关系，只要用心发现、探索，必然会发现其中的规律．二、变式变式l 将直线AB绕点B逆时针方向旋转一定角度，交直线CD于点Q，如图12，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？解连结QP并延长至F．∵∠BPF是△PBQ的外角，∴∠BPF＝∠B＋∠BQP，同理可得∠DPF＝∠D＋∠DQP．∴∠BPF＋∠DPF＝∠B＋∠BQP＋∠D＋∠DQP，即∠BPD＝∠B＋∠D＋∠BQD．变式2 求图13中∠A＋∠B＋∠C＋∠D＋∠E＋LF的度数．解由图12的结论，得∠AGB＝∠A＋∠B＋∠E．又∵∠AGB＝∠CGF，∠CGF＋∠C＋∠D＋LF＝360°，∴∠A＋∠B＋∠C＋∠D∠E＋LF＝360°．。

在不变中寻变，变中把握不变教案第一章：引言1.1 课程目标：让学生理解在不变中寻变，变中把握不变的重要性。

培养学生对变化的观察和思考能力。

1.2 教学内容：介绍变化的普遍性和不可避免性。

讨论在变化中寻找不变的因素的意义。

1.3 教学方法：讲座式教学，引导学生思考和讨论。

1.4 教学工具：投影仪，用于展示相关例证和图像。

1.5 教学步骤：1.5.1 导入：通过展示一组图片，引导学生观察其中的变化和不变之处。

1.5.2 主体讲座：讲解变化的普遍性和不可避免性，以及在变化中寻找不变的因素的意义。

1.5.3 小组讨论：学生分组讨论在各自的生活中经历的变与不变，并分享讨论结果。

第二章：变化的观察与分析2.1 课程目标：培养学生观察和分析变化的能力。

让学生理解变化中的规律性。

变化的类型和特点。

变化中的规律性。

2.3 教学方法：案例分析教学，引导学生观察和分析。

2.4 教学工具：案例资料，用于分析变化的特点和规律性。

2.5 教学步骤：2.5.1 导入：通过展示一个案例，引导学生观察其中的变化。

2.5.2 主体讲座：讲解变化的类型和特点，以及变化中的规律性。

2.5.3 小组讨论：学生分组分析案例中的变化特点和规律性，并分享讨论结果。

第三章：在不变中寻变3.1 课程目标：培养学生识别不变的因素的能力。

让学生理解在不变中寻变的含义和价值。

3.2 教学内容：不变因素的识别和分析。

在不变中寻变的方法和技巧。

3.3 教学方法：小组合作教学，引导学生识别和分析不变因素。

3.4 教学工具：案例资料，用于分析不变因素。

3.5.1 导入：通过展示一个案例，引导学生观察其中的不变因素。

3.5.2 主体讲座：讲解不变因素的识别和分析方法，以及在不变中寻变的含义和价值。

3.5.3 小组合作：学生分组合作分析案例中的不变因素，并分享合作成果。

第四章：变中把握不变4.1 课程目标：培养学生理解变化中的不变因素的能力。

让学生掌握在变中把握不变的方法和技巧。

谈应用“变中抓不变的思路”来解应用题作者：高煌辉来源：《教育教学论坛》2014年第09期摘要：大家都清楚，分数、百分数应用题是小学数学的重要内容，也是小学数学重点和难点之一。

它有其本身的特点和解题规律，尤其是较复杂的分数、百分数应用题，数量之间相依关系显得更加隐蔽、复杂，这就给学生学好这部分内容带来一定的困难。

为了帮助学生学好这部分内容，老师常用的几种解题思路有：图解思路、对应思路、假设思路、转化思路、方程思路、变中抓不变思路等，这里笔者举例来说明应用“变中抓不变思路”来解一些分数应用题。

关键词：帮助；找到；简单中图分类号：G622.0 文献标志码：A 文章编号：1674-9324（2014）09-0249-02大家都清楚，分数、百分数应用题是小学数学的重要内容，也是小学数学重点和难点之一。

它有其本身的特点和解题规律，尤其是较复杂的分数、百分数应用题，数量之间相依关系显得更加隐蔽、复杂，这就给学生学好这部分内容带来一定的困难。

为了帮助学生学好这部分内容，老师常用的几种解题思路有：图解思路、对应思路、假设思路、转化思路、方程思路、变中抓不变思路等，这里我举例来说明应用“变中抓不变思路”来解一些分数应用题。

例1：甲、乙、丙、丁四人共同生产一批零件，甲生产的占其他三人生产总数的■，乙生产的占其他三人生产总数的■，丙生产的占其他三人生产总数的■，已知丁生产了60个，求甲、乙、丙各生产了多少个？分析：要想求甲、乙、丙各生产了多少个，要知道总数，题中只讲到丁生产了60个，关键问题是要求出这60个零件占总数的几分之几，百分率不能直接相加减，所以解题的关键是抓住四人共同生产的这批零件总数不变，因此可以分别把其他三人生产总数看作单位“1”，从而分别求出甲、乙、丙三人生产的零件占总数的几分之几，问题就可以得到解决。

解：（1）甲的产量占总数的几分之几？■÷（1+■）=■（2）乙的产量占总数的几分之几？■÷（1+■）=■（3）丙的产量占总数的几分之几？■÷（1+■）=■（4）这批零件总数是多少？60÷（1-■-■-■）=150（个）（5）甲生产的零件：150×■=30（个）（6）乙生产的零件：150×■=40（个）（7）丙生产零件：150×■=40（个）例2：有大小两个书架，小书架上放的本数是大书架上本数的■，要从小书架上拿出80本放到大架上，这时小书架的书是大书架上书的■，原来两个书架各放多少本书？分析：根据题意可知，两个书架的总数不变，在变量中找到这个不变量，统一以这个不变量为单位“1”进行分率转化找到对应关系，问题就解决了。

2020年第4期教育教学1SCIENCE FANS 1 “变中求不变”思想在概念教学中的渗透概念是人脑对事物本质属性的能动反映。

数学概念是一类特殊的概念，是现实世界中的空间形式和数量的关系及其本质属性在思维中的能动反映。

数学教育的基础是概念教学，若忽略数学概念的教学，那么达到教学目的及教学要求是难以实现的[1]。

1.1 正例强化策略科学的数学思想方法，可以使学生在数学概念的理解和运用上更加得心应手，对概念教学有很大的促进作用。

运用不变的思想在动态过程中找到问题中的联系，充分激发学生的创造性思维，可以有效提高学生创新思维能力，对提升系统知识有关键作用。

对“变中求不变”思想在概念教学中的正例强化策略，主要是向学生强调概念中不变的是本质，要把握概念的实质。

教材中把平行四边形定义为两组对边分别平行的四边形，通常把此作为本质属性，不需要证明。

那么，对任意一个四边形，满足以下任一条件：一组对边平行且相等、对角线互相平分、两组对角分别相等、每一组邻角都互补、两组对边分别相等，也说该四边形是平行四边形，这是从何而来？教师在组织教学活动时，需要通过其他派生的判定条件对定义进行推导。

如利用一组对边平行且相等推出两组对边分别平行”。

已知四边形A B C D ，已知A B ∥C D ,A B =C D ，求证AC ∥BD 。

因为AB ∥CD ，所以∠BAD =∠ADC ,∠ABC =∠BCD ，因为AB =CD ，所以ΔAOB ≌ΔDOC 。

所以AO =OD ,CO =OB 。

又因为∠AOC =∠BOD ，所以ΔAOC ≌ΔBOD 。

故∠CAD =∠ADB ，AC ∥BD 。

其他派生的条件同理可得。

由此可见，上述六种条件可以相互推导，它们都可以作为平行四边形的本质属性来进行图形的判断。

对任意变化的图形，脱离了其中任意一个条件限制，该图形就不是平行四边形，这一点需要着重向学生说明。

每一个概念都具有其本质和非本质的的特点。

在不变中寻变，变中把握不变教案一、教学目标1. 让学生理解“在不变中寻变，变中把握不变”的哲理。

2. 培养学生学会从变化中寻找规律，把握事物的本质。

3. 提高学生分析问题和解决问题的能力。

二、教学内容1. 导入：介绍“在不变中寻变，变中把握不变”的含义。

2. 理论讲解：讲解“在不变中寻变，变中把握不变”的哲理，举例说明其在生活中的应用。

3. 案例分析：分析具体案例，让学生学会从变化中寻找规律，把握事物的本质。

4. 小组讨论：分组讨论如何在生活中运用“在不变中寻变，变中把握不变”的哲理。

5. 总结提升：总结本节课的主要内容，强调“在不变中寻变，变中把握不变”的重要性。

三、教学方法1. 讲授法：讲解“在不变中寻变，变中把握不变”的哲理及应用。

2. 案例分析法：分析具体案例，让学生深入理解哲理。

3. 小组讨论法：分组讨论，培养学生的合作与交流能力。

4. 总结提升法：对本节课内容进行总结，强化学生对哲理的认识。

四、教学准备1. 课件：制作课件，展示相关理论及案例。

2. 案例材料：准备一些生活中的案例，用于教学分析。

3. 分组讨论工具：准备足够的小组讨论材料，如白纸、笔等。

五、教学过程1. 导入：简要介绍“在不变中寻变，变中把握不变”的含义，激发学生的兴趣。

2. 理论讲解：详细讲解“在不变中寻变，变中把握不变”的哲理，并举例说明其在生活中的应用。

3. 案例分析：分析具体案例，让学生学会从变化中寻找规律，把握事物的本质。

4. 小组讨论：将学生分成若干小组，让他们讨论如何在生活中运用“在不变中寻变，变中把握不变”的哲理，并分享讨论成果。

5. 总结提升：对本节课的主要内容进行总结，强调“在不变中寻变，变中把握不变”的重要性，鼓励学生在日常生活中积极实践。

教学反思：在课后，教师应认真反思本节课的教学效果，观察学生对“在不变中寻变，变中把握不变”哲理的理解程度，以及他们在生活中的实际运用情况。

针对存在的问题，及时调整教学方法，以提高教学效果。

在变中求不变，以不变应万变作者：张亚新来源：《教育·教学科研》2022年第02期数学问题千变万化，但是万变不离其宗，许多问题可以通过对比找到其中变化的量，通过变化来激活学生的思维，发现一定的数学规律，对问题进行深入思考，从而把握问题的本质，再以不变的本质应对万变的形式以及具体问题。

《义务教育数学课程标准》明确提出学生能“获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”，在我们平时的教学实践中尤其是低段教学中，对于基础知识和技能，教师往往是比较重视的，也比较容易把握教学目标，但一些教师可能就不会再有所延伸或者拓展，这样很容易忽视学生数学思想的培养。

而在后面高段学习中，其实数学思想的体会与运用尤其重要。

低段学生可能对复杂深度的数学思想理解有困难，但是教师不能“知难避难”，应该结合低段学生的年龄特点设计课堂教学，采用简单活泼的活动形式让学生初步感悟以及理解数学的基本思想与方法。

“变与不变”思想是小学数学的学习中一个重要的思想方法，许多数学问题的解决正是运用了这种思想。

在小学数学教材中，“变与不变”的思想贯穿所有年级，也有很多“变与不变”的素材值得教师好好学习利用，促使学生获得基本的数学思想。

下面，从笔者的几个教学案例看如何在小学低段的教学中渗透“变与不变”的数学思想。

（一）运用“变与不变”思想体会数学概念在小学数学的教学当中，数学概念是基础知识，也是教学的核心内容，想要学习好数学的内容，前提是要有对数学概念的正确理解。

数学的概念比较抽象难懂，小学数学学习中概念性知识比较多，小学生尤其低段学生由于其年龄特点，很难长时间集中注意力，对概念性内容兴趣不高，可能会感觉枯燥乏味。

在教学中，教师应该一边渗透“变与不变”思想，一边把学生的认知以及教学要求紧密地结合起来。

在数学问题中可以找出其中的不变量，利用这些不变量来引导学生观察分析变化量，学生在观察分析对比的过程中，了解概念的内涵，能够更好地体会概念的本质，并将之内化为自己的知识和经验，灵活运用到解决问题的具体情境中去。

竭诚为您提供优质的服务，优质的文档，谢谢阅读/双击去除变中找不变，巧解倍数题有些比或倍数的应用题，两个量是倍数关系，当两个数量发生变化后，倍数关系也发生变化，因此，我们可在变量中寻找不变的量，再进行分析与解答。

例1甲、乙两个同学，某次考试的分数比 5 : 4,如果甲少得20分，乙多得20分，这时他们的分数比是5 :乙求甲、乙两人原来的考试分数各是几分？分析与解答：因为甲、乙两人一个少得20分，一个多得20分, 因此两人的分数之和没有发生变化，原来两人的分数之和份数之和是：5+4=（份），两人分数发生变化以后分数之和的份数是：5+7=12（份）。

因为分数之和没有发生变化，因此可将分数变化前后两人的份数转化成相同：5 : 4=20： 16; 5 : 7=15： 21,这样两人分数变化前后份数均为36份。

甲少得20分，乙多得20分，正好相当于5 （20- 15）份, 因此可得，甲原来考试的分数是：20+ 5X初80（分）；乙原来考试的分数是：20-5X1564 （分），或为：80-5*64 （分）例2、A、b两种商品的价格比7 : 3,如果它们的价格分别上涨42元，那么它们的价格比是7 : 4,求这两种商品原来的价格分别是多少元？分析与解答：因为A、 b 两种商品涨价幅度相同,因此两种商品涨价前后的价格差不变, 因此可将这两种商品涨价前后的份数差调整为相同：7 : 3 = 21 : 9; 7 : 4= 28 : 16。

这样可得A、b两种商品的价格涨价前后均相差点12（21 －9）份,涨价了7（28－21 ）份,正好涨价了42元，因此可得A商品的原价是：42-7X = 126 （元）；b 商品的原价是：42-7X=54 （元），或为：126-7X=54 （元）。

例3、小张和小王每月的收入之比是4: 3,支出之比是18: 13, 他们每月去掉各种开支后都结余300 元,求他们每月的收入分别是多少元？分析与解答：他们两人每月结余的金额数量相同, 因此他们每月的收入减去支出的份数也应该相同：4: 3=20: 15。