2002年杭州市中考数学试卷

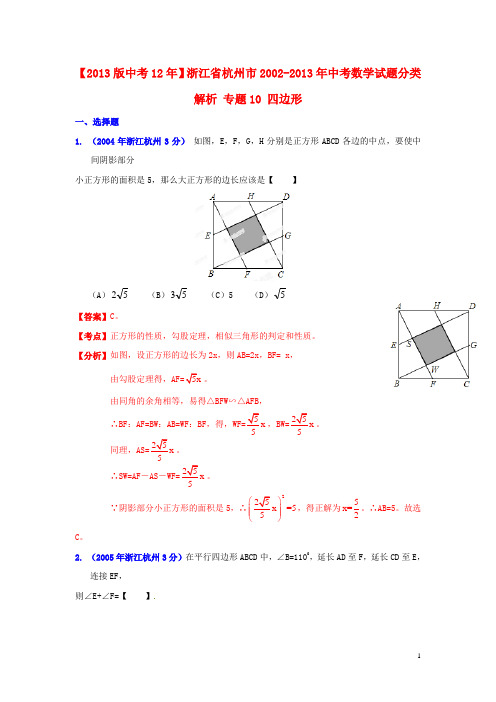
【2013版中考12年】浙江省杭州市2002-2013年中考数学试题分类解析 专题10 四边形一、选择题1. （2004年浙江杭州3分） 如图，E ，F ，G ，H 分别是正方形ABCD 各边的中点，要使中间阴影部分小正方形的面积是5，那么大正方形的边长应该是【 】（A ）52 （B ）53 （C ）5 （D ）5【答案】C 。

【考点】正方形的性质，勾股定理，相似三角形的判定和性质。

【分析】如图，设正方形的边长为2x ，则AB=2x ，BF= x ，由勾股定理得，。

由同角的余角相等，易得△BFW∽△AFB，∴BF：AF=BW ：AB=WF ：BF ，得，，。

同理，。

∴SW=AF－AS －。

∵阴影部分小正方形的面积是5，∴2=5⎫⎪⎪⎝⎭，得正解为5x=2。

∴AB=5。

故选C 。

2. （2005年浙江杭州3分）在平行四边形ABCD 中，∠B=1100，延长AD 至F ，延长CD 至E ，连接EF ，则∠E+∠F=【 】（A）1100（B）300（C）500（D）700【答案】D。

【考点】平行四边形的性质，平行的性质，三角形外角性质。

【分析】∵四边形ABCD为平行四边形，∴AB∥CD，AD∥CB。

∴∠B＋∠C=180°。

∵∠B=110°，∴∠C=70°。

∴∠FDC=70°。

∴∠E+∠F＝70°。

故选D。

3. （2007年浙江杭州3分）下图背景中的点均为大小相同的小正方形的顶点，其中画有两个四边形，下列叙述中正确的是【】A.这两个四边形面积和周长都不相同B. 这两个四边形面积和周长都相同C. 这两个四边形有相同的面积，但Ⅰ的周长大于Ⅱ的周长D. 这两个四边形有相同的面积，但Ⅰ的周长小于Ⅱ的周长【答案】D。

【考点】网格问题，正方形的性质，勾股定理，实数的大小比较。

【分析】设小正方形的边长为1，则两四边形的面积都等于1211=12⨯⨯⨯。

Ⅰ的周长等于。

>1D。

【山西省】25.如图，等腰直角△ABC 的斜边AB = 4，O 是AB 的中点，以O 为圆心的半圆分别与两腰相 切，于点D 、E ，求图中阴影部分的面积（结果用 π表示）． 【北京市海淀区】25．如图，AB 是⊙O 的直径，AE 平分BAF ∠交⊙O 于点E ，过点E 作直线与AF 垂直 交AF 延长线于D 点．且交AB 延长线于C 点． （1）求证：CD 与⊙O 相切于点E ；（2）若415=⋅DE CE ，3=AD ．求⊙O 的直径及AED ∠的正切值． 【南宁市】24．如图，BC 是⊙O 的直径，A 是 弦BD 延长线上一点，切线DE 平分AC 于E ． 求证（1）AC 是⊙O 的切线；（2）若15：23：==AC DB AD ，求⊙O 的直径． 【江西省】24.如图,已知△ABC 内接于⊙O , AE 切 ⊙O 于点A ,BC ∥AE .（1）求证: △ABC 是等腰三角形; （2）设AB =10cm,BC =8cm ，点P 是射线AE 上的点，若以A 、P 、C 为顶点的三角形与△ABC 相似，问这样的点有几个？并求AP 的长.【济南市】29.（本题满分8分）如图，已知 AB = AC +BD ，∠CAB = ∠ABD = 90°,AD 交BC 于P ，⊙P 与AB 相切于点Q .设AC = a ,BD = b (a ≤ b ).（1）求⊙P 的半径r ;（2）以AB 为直径在AB 的上方做半圆O （用尺规作图，保留痕迹，不写作法），请你探索⊙O 与⊙P 的位置关系，做出判断并加以证明；AB CDE.F O ABCE.OACDP Q.OABCDE A（3）设a = 2,b = 4,能否在半圆O 中，再画出两个与⊙P 同样大小的⊙M 和⊙N ，使这3个小圆两两相交，并且每两个小圆的公共部分的面积小于？请说出你的结论，并给出证明.【黄冈市】19.(满分8分)在一服装厂里有大量形状为 等腰直角三角形的边角布料(如图).现找出其中的一种, 测得∠C = 90°,AC = BC =4,今要从这种三角形中剪出一中扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC 的边上,且扇形的弧与△ABC 的其他边相切.请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径).【南京市】31．已知：⊙1O 与⊙2O 外切，⊙1O 的半径R = 2．设⊙2O 的半径是r ． （1）如果⊙1O 与⊙2O 的圆心距d = 4，求r 的值； （2）如果⊙1O 、⊙2O 的公切线中有两条互相垂直，并且r ≤ R ，求r 的值． 【武汉市】41．已知：如图，⊙O 和⊙1O 内切于A ，直 线⊙1O 交⊙O 于另一点B 、交⊙1O 于另一点F ，过B 点 作⊙1O 的切线，切点为D ，交⊙O 于C 点，DE ⊥AB 垂 足为E ．求证：（1）CD = DE ； （2）若将两圆内切改为外切，其他条件不变，（1）中的结论是否成立？请证明你的结论．【福州市】27、已知：半径不等的⊙O 1与⊙O 2相切于点P ,直线AB 、CD 都经过点P ,并且AB 分别交⊙O 1、⊙O 2于A 、B 两点，CD 分别交⊙O 1、⊙O 2于C 、D 两点 （点A 、B 、C 、D 、P 互不重合），连结AC 和BD . （1） 请根据题意画出图形；（2） 根据你所画出的图形，写出一个与题设有关的正确结论，并证明这ABC1OABC D F ..E O个结论 （结论中不能出现题设以外的其他字母）. 【济南市】（两题中任选一题作答）24.（1）在 生活中需测量一些球（如足球、篮球…）的 直径.某校研究性学习小组，通过实验发现下 面的测量方法：如图，将球放在水平的桌面上，在阳光的斜射下，得到球的影子AB ，设光线DA 、CB 分别与球相切于点 E 、F ，则EF 即为球的直径. 若测得AB 的长为41.5cm ，∠ABC =︒37. 请你计 算出球的直径（精确到1cm ）.（2）有一特殊材料制成的质量为30克的泥块，现把它切开大、小两块，将 大泥块放在一架不等臂天平的左盘中，称得质量为27克；有将较小泥块放在该天平的右盘中，称得质量为8克. 若只考虑该天平的臂长不等，其他因素忽略不计，请你依据杠杆的平衡原理，求出较大泥块和较小泥块的质量. 【辽宁省】25．已知：如图，AB 是⊙O 的直 径，C 是⊙O 上一点，连结AC ，过点C 作直 线AB CD ⊥于D （AD ＜DB ），点E 是DB 上 任意一点（点D 、B 除外）直线CE 交⊙O 于 点F ，连结AF 与直线CD 交于点G ．（1）求证；AF AG AC ⋅=2；（2）若点E 是AD （点A 除外）上任意一点，上述结论是否仍然成立？ 若成立．请画出图形并给予证明．若不成立，请说明理由. 【济南市】28.（本题满分7分）如图，AB 、AC 分别是⊙O 的直径和弦，D 为劣弧AC DE ⊥AB 于点H ，交⊙O 于点E ，交AC 于点 F ,P 为ED 的延长线上一点.(1)当△PCF 满足什么条件时，PC 与⊙O 相切.为什么？ .A B C O D GEF︒37ACDFE B..ABC DEFP O【北京市西城区】五、已知：AB 为⊙O 的直径，P 为AB 延长线上的一个动点，过点P 作⊙O 的切线．设切点为C ．（1）当点P 在AB 延长线上的位置如图1 所示时，连结AC ，作∠APC 的平分线，交AC 于点D ，请你测量出∠CDP 的度数；（2）当点P 在AB 延长线上的位置如图2 和图3所示时， 连结AC ，请 你分别在这两 个图中用尺规作∠APC 的平分线（不写作法，保留作图痕迹），设此角平分线交AC 于点D ，然后在这两个图中分别测量出∠CDP 的度数；猜想：∠CDP 的度数是否随点P 在AB 延长线上的位置的变化而变化？请对你的猜想加以证明．【安徽省】30.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行如下讨论：甲同学：这种多边形不一定是正多边形，如圆 内接矩形；乙同学：我发现边数是6时，它也不一定是正 多边形.如图一，△ABC 是正三角形， AD =BE =CF ， 可以证明六边形ADBECF 的各内角相等，但它未必 是正六边形；丙同学：我能证明，边数是5时，它是正多边形，我想，边数是7时，它可能也是正多边形.… …（1）请你说明乙同学构造的六边形各内角相等．图1.COBPAD图2.COBPA图3.COB PA..ABC DF OAB CEFGO图1图2（2）请你证明，各内角都相等的圆内接七边形ABCDEFG（如图二）是正七边形（不必写已知、求证）．（3）根据以上探索过程，提出你的猜想（不必证明）．【江西省】28.如图,正三角形ABC的边长为36厘米,⊙O的半径为r厘米,当圆心O从点A出发,沿着线路AB BC CA运动,回到点A时, ⊙O随着点O的运动而移动.（1）若r =3厘米,求⊙O首次与BC边相切时,AO的长.（2）在⊙O移动过程中,从切点的个数来考虑,相切有几种不同的情况?写出不同的情况下,r的取值范围及相应的切点个数.（3）设⊙O在整个移动过程中,在△ABC内部、⊙O未经过的面积为S,在S ＞0时,求S关于r的函数解析式,并写出自变量r的取值范围.【陕西省】26.(本题满分10分)已知，如图，BC为半圆O的直径，F是半圆上异于B、C的一点，A是弧BF AD⊥BC于点D，BF交AD于点E.（1）求证：BE·BF=BD·BC;（2）试比较线段BD与AE的大小，并说明道理.AB CEF.O()OAB C.O。

浙江省杭州市中考数学试题分类解析 专题11 圆一、选择题1. （2002年浙江杭州3分）过⊙O 内一点M 的最长的弦长为6cm ，最短的弦长为4cm ．则OM 的长为【 】． （A ）3cm （B ）5cm（C ）2cm（D ）3cm【答案】B 。

【考点】垂径定理，勾股定理。

【分析】⊙O 内一点M 的最长的弦是过点M 的直径；最短的弦是过点M 垂直于过点M 的直径的弦。

如图，AB 是最长的弦，CD 是最短的弦，连接OC 。

∵AB=6cm，CD=4cm ；∴OC=OA=3cm，CM=2cm 。

∴2222OM OC CM 325=-=-=（cm ）。

故选B 。

2. （2003年浙江杭州3分）如图，点C 为⊙O 的弦AB 上的一点，点P 为⊙O 上一点，且OC⊥CP，则 有【 】（A ）OC 2＝CA•CB （B ）OC 2＝PA•PB （C ）PC 2＝PA•PB （D ）PC 2＝CA•CB【答案】D。

【考点】垂径定理，相交弦定理。

【分析】延长PC交圆于D，连接OP，OD。

根据相交弦定理，得CP•CD=CA•CB。

∵OP=OD，OC⊥PC，∴PC=CD。

∴PC2=CA•CB。

故选D。

3. （2004年浙江杭州3分）如图，三个半径为3的圆两两外切，且ΔABC的每一边都与其中的两个圆相切，那么ΔABC的周长是【】（A）12+63（B）18+63（C）18+123（D）12+123【答案】B。

【考点】相切圆的性质，等边三角形、矩形的判定和性质，锐角三角函数定义，特殊角的三角函数值。

【分析】∵三圆两两相切，∴外切的△ABC为等边三角形（证明略）。

如图，连接 BO 2，CO 3，分别过点O 1，O 2作BC 的垂线，垂足为D ，E 。

∴BO 2平分∠ABC，∠O 2BC ＝30° 。

∵O 2D⊥BD ，∴22O D 3tan O BC tan30BD 3∠︒＝＝＝。

∵O 2D=3，∴2O D 3BD 33333＝＝＝。

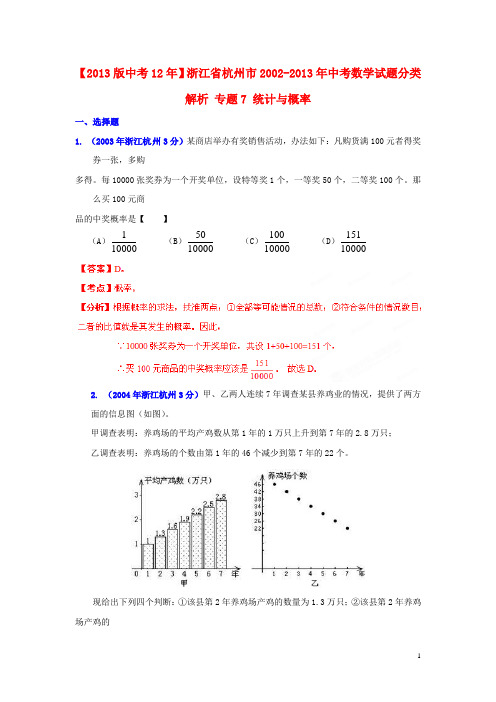
【2013版中考12年】浙江省杭州市2002-2013年中考数学试题分类解析 专题7 统计与概率一、选择题1. （2003年浙江杭州3分）某商店举办有奖销售活动，办法如下：凡购货满100元者得奖券一张，多购多得。

每10000张奖券为一个开奖单位，设特等奖1个，一等奖50个，二等奖100个。

那么买100元商品的中奖概率是【 】（A ）100001 （B ）1000050 （C ）10000100 （D ）100001512. （2004年浙江杭州3分）甲、乙两人连续7年调查某县养鸡业的情况，提供了两方面的信息图（如图）。

甲调查表明：养鸡场的平均产鸡数从第1年的1万只上升到第7年的2.8万只； 乙调查表明：养鸡场的个数由第1年的46个减少到第7年的22个。

现给出下列四个判断：①该县第2年养鸡场产鸡的数量为1.3万只；②该县第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量；③该县这7年养鸡场产鸡的数量逐年增长；④这7年中，第5年该县养鸡场出产鸡的数量最多。

根据甲、乙两人提供的信息，可知其中正确的判断有【 】（A ）3个 （B ）2个 （C ）1个 （D ）0个3. （2005年浙江杭州3分）有一对酷爱运动的年轻夫妇给他们12月大的婴儿拼排3块分别写有“20”“08”和“北京”的字块，如果婴儿能够排成“2008北京”或者“北京2008”，则他们就给婴儿奖励，假设该婴儿能将字块横着正排，那么这个婴儿能得到奖励的概率是【 】（A ）61 （B ）41 （C ）31 （D ）21 【答案】C 。

【考点】概率。

【分析】根据概率的求法，找准两点：①全部等可能情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率。

因此，画树状图得：∵婴儿拼排3块字块的等可能结果有6种，能够排成“2008北京”或者“北京2008”的情况有2种，∴这个婴儿能得到奖励的概率是21=63。

故选C。

4. （2006年浙江杭州大纲卷3分）在某一场比赛前，教练预测：这场比赛我们队有50%的机会获胜，那么相比之下在下面4种情形的哪一种情形下，我们可以说这位教练说得比较准【】A．该队真的赢了这场比赛B．该队真的输了这场比赛C．假如这场比赛可以重复进行10场而这个队赢了6场D．假如这场比赛可以重复进行100场而这个队赢了51场5. （2006年浙江杭州课标卷3分）在某一场比赛前，教练预测：这场比赛我们队有50%的机会获胜，那么相比之下在下面4种情形的哪一种情形下，我们可以说这位教练说得比较准【】A．该队真的赢了这场比赛B．该队真的输了这场比赛C．假如这场比赛可以重复进行10场而这个队赢了6场D．假如这场比赛可以重复进行100场而这个队赢了51场【答案】D。

【2013版中考12年】浙江省杭州市2002-2013年中考数学试题分类解析专题4 图形的变换一、选择题1. （2002年浙江杭州3分）在时刻8∶30，时钟上的时针和分针之间的夹角为【】．（A）85°（B）75°（C）70°（D）60°【答案】B。

【考点】钟面角。

【分析】∵时针走一圈(3600)要12小时，即速度为003603600.5/121260==⨯分小分钟时钟；分针走一圈(3600)要1小时，即速度为000 3603606/160==分小分钟时钟。

∴时针从数字8开始到8点30分，走过的角度为30×0.50=150，即时针在8点30分的位置离开数字6的角度为300×2+15=750 (钟面360度被分成了12等份,每份是300)。

又∵分针从8点(数字12)开始到8点30分时，分针指向数字6，所以8点30分时，时钟上时针和分针夹角750。

故选B。

2. （2002年浙江杭州3分）为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路．现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里），则能把电力输送到这四个村庄的输电线路的最短总长度应该是【】．（A）19.5 （B）20.5 （C）21.5 （D）25.5【答案】B。

3. （2006年浙江杭州大纲卷3分）边长为4的正方形绕一条边旋转一周，所得几何体的侧面积等于【 】A ．16B ．16πC ．32πD ．64π【答案】C 。

【考点】圆柱的计算。

【分析】边长为4的正方形绕一条边旋转一周，所得几何体是圆柱体，根据圆柱的侧面积公式圆柱侧面积=底面周长×高可得：π×4×2×4=32π。

故选C 。

4. （2006年浙江杭州大纲卷3分）如图，把△PQR 沿着PQ 的方向平移到△P′Q′R′的位置，它们重叠部分的面积是△PQR 面积的一半，若PQ ＝2，则此三角形移动的距离PP′是【 】A ．12B ．22C ．1D 21-【答案】D 。

2002年浙江省杭州市各类高中招生文化考试英语试卷考生须知：1、本试卷满分120分，考试时间100分钟。

2、答题前，在答题纸上写姓名和准考证号。

3、必须在答题纸的对应答题位置上答题，写在其他地方无效。

1至60小题在答题纸上涂黑作答，答题方式详见答题纸上的说明。

4、做听力题时，先将答案划在试卷上。

录音内容结束后，你将有一分钟的时间将试卷上的答案转涂到答题纸上。

5、考试结束后，试题卷和答题纸一并上交。

试题卷I. 听力部分（25分）一、听对话回答问题(共5小题，计10分)听下面一段对话，回答第1和第2两个小题。

现在，你有10秒钟的时间阅读这两题。

1. What did the man want to do?A. To ask the woman several questions about his computer study.B. To have supper together with the woman at a restaurantC. To tell the woman that he will be free at eight this evening.2. What have we learned from what the woman said?A. The man is not welcome to the woman's home.B. The man will go to the woman' s home about eight this evening.C. The woman' won't be free until eight this evening.听下面一段对话，回答第3至第5小题。

现在，你有15秒钟的时间阅读这三题。

3. What are the two speakers talking about?A. Some places of interest.B. A few accidents these days.C. Traveling by plane.4. Where is the woman going?A. Paris.B. London.C. Berlin.5. The woman hates flying. How many reasons (理由) are mentioned in the conversation then?A. Only one.B. Three.C. Two.二、听独白回答问题(共5小题，计10分)听下面一段独白，独白后有5个小题，从A、B、C三个选项中选出最佳选项。

【2013版中考12年】浙江省杭州市2002-2013年中考数学试题分类解析 专题1 实数一、选择题1. （2002年浙江杭州3分）下列各组数中互为相反数的是【 】．（A ）2-与12- （B ）2-与2 （C ）2- （D ）2-2. （2003年浙江杭州3分） 计算 220032003])5[(04.0-⨯ 得【 】（A ）1 （B ）－1 （C ）200351 （D ）200351-【答案】A 。

【考点】幂的乘方与积的乘方。

【分析】20032003220032200320032003200320030.04[(5)]0.04[5]0.04250.042511⨯-=⨯-=⨯=⨯==（）（）。

故选A 。

3. （2003年浙江杭州3分） 已知 a=，b =，则的值为【 】 （A ）3 （B ）4 （C ）5 （D ）64.（2004年浙江杭州3分） 蜗牛前进的速度每秒只有1.5毫米，恰好是某人步行速度的1000分之一， 那么此人步行的速度大约是每小时【 】（A ）9公里 （B ）5.4公里 （C ）900米 （D ）540米5. （2004年浙江杭州3分） 有下列说法：①有理数和数轴上的点一一对应；②不带根号的数一定是有理 数；③负数没有立方根；④17-是17的平方根。

其中正确的有【 】（A ）0个 （B ）1个 （C ）2个 （D ）3个6. （2004年浙江杭州3分） 若数轴上表示数x 的点在原点的左边，则化简3x 的结果是【 】（A ）-4x （B ）4x （C ）-2x （D ）2x【答案】C 。

【考点】实数与数轴，二次根式的性质，绝对值的性质。

【分析】利用实数与数轴的关系判断x 的符号，再利用二次根式的性质，绝对值的性质解题：∵数轴上表示数x 的点在原点的左边，∴x＜0。

∴3x 3x x 2x 2x =-==-。

故选C 。

7. （2005年浙江杭州3分）设a=23-，b=32-，c=25-，则a ，b ，c 的大小关系是【 】（A ）a>b>c （B ）a> c > b （C ）c>b>a （D ）b>c>a8. （2005年浙江杭州3分）磁悬浮列车是一种科技含量很高的新型交通工具，它有速度快、爬坡能力强，能耗低等优点，它每个座位的平均能耗仅为飞机每个座位平均能耗的三分之一，汽车每个座位平均能耗的 70%，那么，汽车每个座位的平均能耗是飞机每个座位平均能耗的【 】（A ）73 （B ）37 （C ）2110 （D ）10219. （2006年浙江杭州大纲卷3分）11(2)()222⨯-+-⨯=【 】 A ．－2B ．0C ．1D ．2 【答案】A 。

【2013版中考12年】浙江省杭州市2002-2013年中考数学试题分类解析 专题9 三角形一、选择题1. （2002年浙江杭州3分）1米长的标杆直立在水平的地面上，它在阳光下的影长为0.8米；此时，若某电视塔的影长为100米，则此电视塔的高度应是【 】．（A ）80米 （B ）85米 （C ）120米 （D ）125米2. （2002年浙江杭州3分）如果直角三角形的三条边为2，4，a ，那么a 的取值可以有【 】．（A ）0个 （B ）1个 （C ）2个 （D ）3个【答案】C 。

【考点】勾股定理逆定理，分类思想的应用。

【分析】直角三角形的三条边为2，4，a ，可以4 或a 是斜边。

若4是斜边，则由2222+a =4取正解若a 是斜边，则由2222+4=a 取正解。

∴ a 的取值可以有2个。

故选C 。

3. （2002年浙江杭州3分）在△ABC 中，∠A、∠B 都是锐角，且sin A 12=，cos B =则△ABC 三个角的大小关系是【 】．（A ）∠C>∠A>∠B（B ）∠B>∠C>∠A （C ）∠A>∠B>∠C （D ）∠C>∠B>∠A 【答案】D 。

【考点】锐角三角函数定义，特殊角的三角函数值，三角形内角和定理。

【分析】∵1sin A 2=，cos B =0，∠B=450。

∴∠C=1800－300－450=1050。

∴∠C>∠B>∠A。

故选D 。

4. （2003年浙江杭州3分）要判断如图ΔABC 的面积是ΔDBC 面积的几倍，只用一把仅有刻度的直尺，需要度量的次数最少是【 】（A ）3次 （B ）2次 （C ）1次 （D ）3次以上【答案】C 。

【考点】三角形的面积，相似三角形的判定和性质。

【分析】根据同底三角形的面积比等于高之比，即可得到答案：如图，连接AD 并延长交BC 于M ，过点A 作AP⊥BC 于点P ，过点D 作DE⊥BC 于点E ， ∵DE∥AP，∴△AMP∽△DME。

浙江省杭州市中考数学试卷一．选择题（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的．注意可以用多种不同的方法来选取正确答案．1．（杭州）下列“表情图”中，属于轴对称图形的是（）A．B．C．D．考点：轴对称图形．分析：根据轴对称的定义，结合各选项进行判断即可．解答：解：A．不是轴对称图形，故本选项错误；B．不是轴对称图形，故本选项错误；C．不是轴对称图形，故本选项错误；D．是轴对称图形，故本选项正确；故选D．点评：本题考查了轴对称图形的知识，判断轴对称的关键寻找对称轴，属于基础题．2．（杭州）下列计算正确的是（）A．m3+m2=m5B．m3m2=m6C．（1﹣m）（1+m）=m2﹣1 D．考点：平方差公式；合并同类项；同底数幂的乘法；分式的基本性质．分析：根据同类项的定义，以及同底数的幂的乘法法则，平方差公式，分式的基本性质即可判断．解答：解：A．不是同类项，不能合并，故选项错误；B．m3m2=m5，故选项错误；C．（1﹣m）（1+m）=1﹣m2，选项错误；D．正确．故选D．点评：本题考查了同类项的定义，以及同底数的幂的乘法法则，平方差公式，分式的基本性质，理解平方差公式的结构是关键．3．（杭州）在▱ABCD中，下列结论一定正确的是（）A．AC⊥BD B．∠A+∠B=180°C．AB=AD D．∠A≠∠C考点：平行四边形的性质．分析：由四边形ABCD是平行四边形，可得AD∥BC，即可证得∠A+∠B=180°．解答：解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠A+∠B=180°．故选B．点评：此题考查了平行四边形的性质．此题比较简单，注意掌握数形结合思想的应用．4．（杭州）若a+b=3，a﹣b=7，则ab=（）A．﹣10 B．﹣40 C．10 D．40考点：完全平方公式．分析：联立已知两方程求出a与b的值，即可求出ab的值．解答：解：联立得：，解得：a=5，b=﹣2，则ab=﹣10．故选A．点评：此题考查了解二元一次方程组，求出a与b的值是解本题的关键．5．（杭州）根据～杭州市实现地区生产总值（简称GDP，单位：亿元）统计图所提供的信息，下列判断正确的是（）A．～杭州市每年GDP增长率相同B．杭州市的GDP比翻一番C．杭州市的GDP未达到5500亿元D．～杭州市的GDP逐年增长考点：条形统计图．分析：根据条形统计图可以算～GDP增长率，～GDP增长率，进行比较可得A的正误；根据统计图可以大约得到和GDP，可判断出B的正误；根据条形统计图可得杭州市的GDP，可判断出C的正误，根据条形统计图可直接得到～杭州市的GDP逐年增长．解答：解：A．～GDP增长率约为：=，～GDP增长率约为=，增长率不同，故此选项错误；B．杭州市的GDP约为7900，GDP约为4900，故此选项错误；C．杭州市的GDP超过到5500亿元，故此选项错误；D．～杭州市的GDP逐年增长，故此选项正确，故选：D．点评：本题考查的是条形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．6．（杭州）如图，设k=（a＞b＞0），则有（）A．k＞2 B．1＜k＜2 C．D．考点：分式的乘除法．分析：分别计算出甲图中阴影部分面积及乙图中阴影部分面积，然后计算比值即可．解答：解：甲图中阴影部分面积为a2﹣b2，乙图中阴影部分面积为a（a﹣b），则k====1+，∵a＞b＞0，∴0＜＜1，故选B．点评：本题考查了分式的乘除法，会计算矩形的面积及熟悉分式的运算是解题的关键．7．（杭州）在一个圆中，给出下列命题，其中正确的是（）A．若圆心到两条直线的距离都等于圆的半径，则这两条直线不可能垂直B．若圆心到两条直线的距离都小于圆的半径，则这两条直线与圆一定有4个公共点C．若两条弦所在直线不平行，则这两条弦可能在圆内有公共点D．若两条弦平行，则这两条弦之间的距离一定小于圆的半径考点：直线与圆的位置关系；命题与定理．分析：根据直线与圆的位置关系进行判断即可．解答：解：A．圆心到两条直线的距离都等于圆的半径时，两条直线可能垂直，故本选项错误；B．当两圆经过两条直线的交点时，圆与两条直线有三个交点；C．两条平行弦所在直线没有交点，故本选项正确；D．两条平行弦之间的距离一定小于直径，但不一定小于半径，故本选项错误，故选C．点评：本题考查了直线与圆的位置关系、命题与定理，解题的关键是熟悉直线与圆的位置关系．8．（杭州）如图是某几何体的三视图，则该几何体的体积是（）A．B．C．D．考点：由三视图判断几何体．分析：由三视图可看出：该几何体是﹣个正六棱柱，其中底面正六边形的边长为6，高是2．根据正六棱柱的体积=底面积×高即可求解．解答：解：由三视图可看出：该几何体是﹣个正六棱柱，其中底面正六边形的边长为6，高是2，所以该几何体的体积=6××62×2=108．故选C．点评：本题考查了由三视图求原几何体的体积，正确恢复原几何体是解决问题的关键．9．（杭州）在Rt△ABC中，∠C=90°，若AB=4，sinA=，则斜边上的高等于（）A．B．C．D．考点：解直角三角形．分析：在直角三角形ABC中，由AB与sinA的值，求出BC的长，根据勾股定理求出AC的长，根据面积法求出CD的长，即为斜边上的高．解答：解：根据题意画出图形，如图所示，在Rt△ABC中，AB=4，sinA=，∴BC=ABsinA=2.4，根据勾股定理得：AC==3.2，∵S△ABC=AC•BC=AB•CD，∴CD==．故选B点评：此题考查了解直角三角形，涉及的知识有：锐角三角函数定义，勾股定理，以及三角形的面积求法，熟练掌握定理及法则是解本题的关键．10．（杭州）给出下列命题及函数y=x，y=x2和y=①如果，那么0＜a＜1；②如果，那么a＞1；③如果，那么﹣1＜a＜0；④如果时，那么a＜﹣1．则（）A．正确的命题是①④B．错误的命题是②③④C．正确的命题是①②D．错误的命题只有③考点：二次函数与不等式（组）；命题与定理．分析：先确定出三函数图象的交点坐标为（1，1），再根据二次函数与不等式组的关系求解即可．所以，交点坐标为（1，1），根据对称性，y=x和y=在第三象限的交点坐标为（﹣1，﹣1），①如果，那么0＜a＜1正确；②如果，那么a＞1或﹣1＜a＜0，故本小题错误；③如果，那么a值不存在，故本小题错误；④如果时，那么a＜﹣1正确．综上所述，正确的命题是①④．故选A．点评：本题考查了二次函数与不等式组的关系，命题与定理，求出两交点的坐标，并准确识图是解题的关键．二．填空题（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案11．（杭州）32×3.14+3×（﹣9.42）= ．考点：有理数的混合运算．分析：根据32×3.14+3×（﹣9.42）=3×9.42﹣3×（﹣9.42）即可求解．解答：解：原式=3×9.42﹣3×（﹣9.42）=0．故答案是：0．点评：本题考查了有理数的混合运算，理解运算顺序是关键．12．（杭州）把7的平方根和立方根按从小到大的顺序排列为．考点：实数大小比较．专题：计算题．分析：先分别得到7的平方根和立方根，然后比较大小．解答：解：7的平方根为﹣，；7的立方根为，所以7的平方根和立方根按从小到大的顺序排列为﹣＜＜．故答案为：﹣＜＜．点评：本题考查了实数大小比较：正数大于0，负数小于0；负数的绝对值越大，这个数越小．13．（杭州）在Rt△ABC中，∠C=90°，AB=2BC，现给出下列结论：①sinA=；②cosB=；③tanA=；④tanB=，其中正确的结论是（只需填上正确结论的序号）考点：特殊角的三角函数值；含30度角的直角三角形．专题：探究型．分析：先根据题意画出图形，再由直角三角形的性质求出各角的度数，由特殊角的三角函数值即可得出结论．解答：解：如图所示：∵在Rt△ABC中，∠C=90°，AB=2BC，∴sinA==，故①错误；∴∠B=60°，∴cosB=cos60°=，故②正确；∵∠A=30°，∴tanA=tan30°=，故③正确；∵∠B=60°，∴tanB=tan60°=，故④正确．故答案为：③③④．点评：本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．14．（杭州）杭州市某4所高中近两年的最低录取分数线如下表（单位：分），设4所高中和的平均最低录取分数线分别为，，则= 分杭州市某4所高中最低录取分数线统计表学校2011年2012年杭州A中438 442杭州B中435 442杭州C中435 439杭州D中435 439考点：算术平均数．分析：先算出的平均最低录取分数线和的平均最低录取分数线，再进行相减即可．解答：解：的平均最低录取分数线=（438+435+435+435）÷4=435.75（分），的平均最低录取分数线=（442+442+439+439）÷4=440.5（分），则=440.5﹣435.75=4.75（分）；故答案为：4.75．点评：此题考查了算术平均数，掌握平均数的计算公式是解题的关键，是一道基础题，比较简单．15．（杭州）四边形ABCD是直角梯形，AB∥CD，AB⊥BC，且BC=CD=2，AB=3，把梯形ABCD分别绕直线AB，CD旋转一周，所得几何体的表面积分别为S1，S2，则|S1﹣S2|= （平方单位）考点：圆锥的计算；点、线、面、体；圆柱的计算．分析：梯形ABCD分别绕直线AB，CD旋转一周所得的几何体的表面积的差就是AB和CD旋转一周形解答：解：AB旋转一周形成的圆柱的侧面的面积是：2π×2×3=12π；AC旋转一周形成的圆柱的侧面的面积是：2π×2×2=8π，则|S1﹣S2|=4π．故答案是：4π．点评：本题考查了图形的旋转，理解梯形ABCD分别绕直线AB，CD旋转一周所得的几何体的表面积的差就是AB和CD旋转一周形成的圆柱的侧面的差是关键．16．（杭州）射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=2cm，QM=4cm．动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心，cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值（单位：秒）考点：切线的性质；等边三角形的性质．专题：分类讨论．分析：求出AB=AC=BC=4cm，MN=AC=2cm，∠BMN=∠BNM=∠C=∠A=60°，分为三种情况：画出图形，结合图形求出即可；解答：解：∵△ABC是等边三角形，∴AB=AC=BC=AM+MB=4cm，∠A=∠C=∠B=60°，∵QN∥AC，AM=BM．∴N为BC中点，∴MN=AC=2cm，∠BMN=∠BNM=∠C=∠A=60°，分为三种情况：①如图1，当⊙P切AB于M′时，连接PM′，则PM′=cm，∠PM′M=90°，∵∠PMM′=∠BMN=60°，∴M′M=1cm，PM=2MM′=2cm，∴QP=4cm﹣2cm=2cm，即t=2；②如图2，当⊙P于AC切于A点时，连接PA，则∠CAP=∠APM=90°，∠PMA=∠BMN=60°，AP=cm，∴PM=1cm，∴QP=4cm﹣1cm=3cm，即t=3，当当⊙P于AC切于C点时，连接PC，则∠CP′N=∠ACP′=90°，∠P′NC=∠BNM=60°，CP′=cm，∴P′N=1cm，∴QP=4cm+2cm+1cm=7cm，即当3≤t≤7时，⊙P和AC边相切；③如图1，当⊙P切BC于N′时，连接PN′3则PN′=cm，∠PM\N′N=90°，∵∠PNN′=∠BNM=60°，∴N′N=1cm，PN=2NN′=2cm，∴QP=4cm+2cm+2cm=8cm，即t=8；故答案为：t=2或3≤t≤7或t=8．点评：本题考查了等边三角形的性质，平行线的性质，勾股定理，含30度角的直角三角形性质，切线的性质的应用，主要考查学生综合运用定理进行计算的能力，注意要进行分类讨论啊．三．解答题（本题有7个小题，共66分）解答应写出文字说明，证明过程或推演步骤．如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以．17．（杭州）如图，四边形ABCD是矩形，用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q（不写作法，保留作图痕迹）．连结QD，在新图形中，你发现了什么？请写出一条．考点：作图—复杂作图．分析：根据角平分线的作法以及线段垂直平分线的作法得出Q点位置，进而利用垂直平分线的作法得出解答：解：如图所示：发现：DQ=AQ或者∠QAD=∠QDA等等．点评：此题主要考查了复杂作图以及线段垂直平分线的作法和性质等知识，熟练应用其性质得出系等量关系是解题关键．18．（杭州）当x满足条件时，求出方程x2﹣2x﹣4=0的根．考点：解一元二次方程-公式法；解一元一次不等式组．分析：通过解一元一次方程组求得2＜x＜4．然后利用求根公式x=求得方程程x2﹣2x﹣4=0的根，由x的取值范围来取舍该方程的根．解答：解：由求得，则2＜x＜4．解方程x2﹣2x﹣4=0可得x1=1+，x2=1﹣，∵2＜＜3，∴3＜1+＜4，符合题意∴x=1+．点评：本题考查了解一元二次方程﹣﹣公式法，解一元一次不等式组．要会熟练运用公式法求得一元二次方程的解．19．（杭州）如图，在等腰梯形ABCD中，AB∥DC，线段AG，BG分别交CD于点E，F，DE=CF．求证：△GAB是等腰三角形．考点：等腰梯形的性质；全等三角形的判定与性质；等腰三角形的判定．专题：证明题．分析：由在等腰梯形ABCD中，AB∥DC，DE=CF，利用SAS，易证得△ADE≌△BCF，即可得∠DAE=∠CBF，则可得∠GAB=∠GBA，然后由等角对等边，证得：△GAB是等腰三角形．∴∠D=∠C，∠DAB=∠CBA，在△ADE和△BCF中，，∴△ADE≌△BCF（SAS），∴∠DAE=∠CBF，∴∠GAB=∠GBA，∴GA=GB，即△GAB为等腰三角形．点评：此题考查了等腰梯形的性质、全等三角形的判定与性质以及等腰三角形的判定．此题难度不大，注意掌握数形结合思想的应用．20．（杭州）已知抛物线y1=ax2+bx+c（a≠0）与x轴相交于点A，B（点A，B在原点O两侧），与y轴相交于点C，且点A，C在一次函数y2=x+n的图象上，线段AB长为16，线段OC长为8，当y1随着x的增大而减小时，求自变量x的取值范围．考点：二次函数的性质；抛物线与x轴的交点．专题：分类讨论．分析：根据OC的长度确定出n的值为8或﹣8，然后分①n=8时求出点A的坐标，然后确定抛物线开口方向向下并求出点B的坐标，再求出抛物线的对称轴解析式，然后根据二次函数的增减性求出x的取值范围；②n=﹣8时求出点A的坐标，然后确定抛物线开口方向向上并求出点B的坐标，再求出抛物线的对称轴解析式，然后根据二次函数的增减性求出x的取值范围．解答：解：根据OC长为8可得一次函数中的n的值为8或﹣8．分类讨论：①n=8时，易得A（﹣6，0）如图1，∵抛物线经过点A、C，且与x轴交点A、B在原点的两侧，∴抛物线开口向下，则a＜0，∵AB=16，且A（﹣6，0），∴B（10，0），而A、B关于对称轴对称，∴对称轴直线x==2，要使y1随着x的增大而减小，则a＜0，∴x＞2；（2）n=﹣8时，易得A（6，0），如图2，∵抛物线过A、C两点，且与x轴交点A，B在原点两侧，∴抛物线开口向上，则a＞0，∵AB=16，且A（6，0），∴B（﹣10，0），而A、B关于对称轴对称，∴对称轴直线x==﹣2，要使y1随着x的增大而减小，且a＞0，∴x＜﹣2．点评：本题考查了二次函数的性质，主要利用了一次函数图象上的点的坐标特征，二次函数的增减性，难点在于要分情况讨论．21．（杭州）某班有50位学生，每位学生都有一个序号，将50张编有学生序号（从1号到50号）的卡片（除序号不同外其它均相同打乱顺序重新排列，从中任意抽取1张卡片（1）在序号中，是20的倍数的有：20，40，能整除20的有：1，2，4，5，10（为了不重复计数，20只计一次），求取到的卡片上序号是20的倍数或能整除20的概率；（2）若规定：取到的卡片上序号是k（k是满足1≤k≤50的整数），则序号是k的倍数或能整除k（不重复计数）的学生能参加某项活动，这一规定是否公平？请说明理由；（3）请你设计一个规定，能公平地选出10位学生参加某项活动，并说明你的规定是符合要求的．考点：游戏公平性．分析：（1）由在序号中，是20的倍数的有：20，40，能整除20的有：1，2，4，5，10（为了不重复计数，20只计一次），直接利用概率公式求解即可求得答案；（2）由无论k取何值，都能被1整除，则序号为1的学生被抽中的概率为1，即100%，而很明显抽到其他序号学生概率不为100%．可知此游戏不公平；（3）可设计为：先抽出一张，记下数字，然后放回．若下一次抽到的数字与之前抽到过的重复，则不记数，放回，重新抽取．不断重复，直至抽满10个不同的数字为止．解答：解：（1）∵在序号中，是20的倍数的有：20，40，能整除20的有：1，2，4，5，10（为了不重复计数，20只计一次），∴是20倍数或者能整除20的数有7个，则取到的卡片上序号是20的倍数或能整除20的概率为：；（2）不公平，∵无论k取何值，都能被1整除，则序号为1的学生被抽中的概率为1，即100%，而很明显抽到其他序号学生概率不为100%．∴不公平；（3）先抽出一张，记下数字，然后放回．若下一次抽到的数字与之前抽到过的重复，则不记数，放回，重新抽取．不断重复，直至抽满10个不同的数字为止．（为保证每个数字每次被抽到的概率都是）点评：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．22．（杭州）（1）先求解下列两题：①如图①，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数；②如图②，在直角坐标系中，点A在y轴正半轴上，AC∥x轴，点B，C的横坐标都是3，且BC=2，点D在AC上，且横坐标为1，若反比例函数的图象经过点B，D，求k的值．（2）解题后，你发现以上两小题有什么共同点？请简单地写出．考点：等腰三角形的性质；反比例函数图象上点的坐标特征．分析：（1）①根据等边对等角可得∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，然后用∠A表示出∠EDM，计算即可求解；②先根据反比例函数图象上的点的坐标特征表示出点B的坐标，再表示出点C的坐标，然后根据AC∥x 轴可得点C、D的纵坐标相同，从而表示出点D的坐标，再代入反比例函数解析式进行计算即可得解．（2）从数学思想上考虑解答．解答：解：（1）①∵AB=BC=CD=DE，∴∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，根据三角形的外角性质，∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，又∵∠EDM=84°，∴∠A+3∠A=84°，解得，∠A=21°；②∵点B在反比例函数y=图象上，点B，C的横坐标都是3，∴点B（3，），∵BC=3，∴点C（3，+2），∵AC∥x轴，点D在AC上，且横坐标为1，∴A（1，+2），∵点A也在反比例函数图象上，∴+2=k，解得，k=3；（2）用已知的量通过关系去表达未知的量，使用转换的思维和方法．（开放题）点评：本题考查了等腰三角形两底角相等的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，以及反比例函数图象上点的坐标特征，是基础题．23．（杭州）如图，已知正方形ABCD的边长为4，对称中心为点P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=45°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1．（1）求证：∠APE=∠CFP；（2）设四边形CMPF的面积为S2，CF=x，．①求y关于x的函数解析式和自变量x的取值范围，并求出y的最大值；②当图中两块阴影部分图形关于点P成中心对称时，求y的值．考点：四边形综合题．分析：（1）利用正方形与三角形的相关角之间的关系可以证明结论；（2）本问关键是求出y与x之间的函数解析式．①首先分别用x表示出S1与S2，然后计算出y与x的函数解析式．这是一个二次函数，求出其最大值；②注意中心对称、轴对称的几何性质．解答：（1）证明：∵∠EPF=45°，∴∠APE+∠FPC=180°﹣45°=135°；而在△PFC中，由于PF为正方形ABCD的对角线，则∠PCF=45°，则∠CFP+∠FPC=180°﹣45°=135°，∴∠APE=∠CFP．（2）解：①∵∠APE=∠CFP，且∠FCP=∠PAE=45°，∴△APE∽△CPF，则．而在正方形ABCD中，AC为对角线，则AC=AB=，又∵P为对称中心，则AP=CP=，∴AE===．如图，过点P作PH⊥AB于点H，PG⊥BC于点G，P为AC中点，则PH∥BC，且PH=BC=2，同理PG=2．S△APE==×2×=，∵阴影部分关于直线AC轴对称，∴△APE与△APN也关于直线AC对称，则S四边形AEPN=2S△APE=；而S2=2S△PFC=2×=2x，∴S1=S正方形ABCD﹣S四边形AEPN﹣S2=16﹣﹣2x，∴y===+﹣1．∵E在AB上运动，F在BC上运动，且∠EPF=45°，∴2≤x≤4．令=a，则y=﹣8a2+8a﹣1，当a==，即x=2时，y取得最大值．而x=2在x的取值范围内，代入x=2，则y最大=4﹣2﹣1=1．∴y关于x的函数解析式为：y=+﹣1（2≤x≤4），y的最大值为1．②图中两块阴影部分图形关于点P成中心对称，而此两块图形也关于直线AC成轴对称，则阴影部分图形自身关于直线BD对称，则EB=BF，即AE=FC，∴=x，解得x=，代入x=，得y=﹣2．点评：本题是代数几何综合题，考查了正方形的性质、相似三角形、二次函数的解析式与最值、几何变换（轴对称与中心对称）、图形面积的计算等知识点，涉及的考点较多，有一定的难度．本题重点与难点在于求出y与x的函数解析式，在计算几何图形面积时涉及大量的计算，需要细心计算避免出错．。