不可能的图形

两可图1在这个图中，你看见的是一个老妇人还是一个年轻的少女？她们都存在在于插图中，但你不可能同时看见老妇人和少女。

一旦你知觉到这两种图形轮廓，看一看你是否能够在这两种图形轮廓之间来回转换。

两可图2在上图中，你看见了什么？你看见的是两个头，还是一个花瓶的轮廓？两可图3上面这幅图你看到了什么？是两个老人晚年的相聚，还是少女在倾听两个快乐的流浪歌手在弹唱？两可图3上面这幅图，你看到的是一位少女的脸还是一位萨克斯演奏家？两可图评注：根据人的不同知识背景或心理状态，同一个事物，不同的人会有不同的看法。

这和人的知觉选择性有关。

知觉选择性是指人根据当前的需要，对外来刺激有选择地作为知觉对象进行组织加工的过程。

这就是说，我们并不是对同时作用于感觉器官的所有刺激都进行反映，而是选择一个或几个刺激。

这些被选择的刺激就是知觉对象，其他没有被选择的就成了知觉背景。

知觉对象和知觉背景之间的关系是相对的。

此时的知觉对象可以成为彼时的知觉对象，而此时的知觉背景也可以成为彼时的知觉对象，它们之间是可以不断发生对换的。

当然，这种选择性会受到我们已有的知识经验、生活经历以及兴趣爱好等的影响。

"我们对世界的感知，部分依赖于对客观事物的感觉，另一部分---- 可能是更重要的的一部分，来自于我们的思维。

"---- William James 都说"耳听为虚，眼见为实"，可是我们的眼睛所见到的都是真实的吗？当你看了下面的心理错觉图片之后就会有一个比较客观的认识了。

如果大家想知道为什么会出现这些现象的话，可以看看后面的解释。

1缪勒－莱耶错觉2闪烁的格子人们在知觉两个相对立的颜色时，这两种相对立的颜色导致一种叫做侧抑制的生理机制，这个机制能使被白色环绕的区域显得更黑，相反，能使被黑色环绕的区域显得更白。

由于在看图的过程中，眼睛不停的跳动，使得侧抑制不停的产生，从而使得上图中出现了闪烁的黑点。

3深度知觉看着图形，慢慢移动你的眼睛，中间的圆形部分看起来是不是与其它的图形分离开来4咖啡墙错觉看一看，上面的这些线条是平行的吗？用尺子量一量，看看你的判断是否正确。

不可能图形的精品之作作者：
来源：《初中生世界·七年级》2013年第12期
不可能立体框架
右边几幅图画中的主体形象都是一个类似六面体的框架，但是仔细观察你就会发现，这些立体框架是不可能图形，根本无法造出来.
荷兰艺术家埃舍尔在1948年创作的名作《互绘的手》.
在一块四角被钉住的图板上，一只手被另一只手所描绘，与此同时，被描绘的手又画着另一只手. 平面的线描袖口贴在画板上，而画中的主体，两只拿着笔互绘的手则凸显在画板上，立体感十足.
瑞士艺术家普瑞特创作的不可能图形《晒台》，展示的是地坪与晒台上的工人们在协作施工的场景，感觉像在同一平面却又不在同一平面.
这是埃舍尔1960年创作的石板画《升与降》. 他在二维的画面上创造出一个不可能的三维图形，还不让你轻易地看出其中的奥秘. 两队士兵在一座城堡里走楼梯，一队士兵是一直上楼
梯，累得要死；另一队相向的士兵下楼梯，轻松自在地往下走. 如此走法，按正常道理两队人应该越走分离越远，但是图中这两队人却走成了个循环，这到底是怎么一回事？
《瀑布》是埃舍尔1961年的石版画. 楼顶水槽的水冲下来，带动底层的水轮转动. 由此推
动水向前流去，流水竟然会一直流呀流，流向楼顶水槽再冲下来，转动水轮……如此循环不止.
《相对论》是埃舍尔1953年的石版画. 也是他利用透视原理和光影效果画的一幅杰作.不
断地切换视线，你看到上楼的人、下楼的人都走得很合理，什么叫上，什么叫下，什么叫正面，什么叫背面，这些都是相对的.。

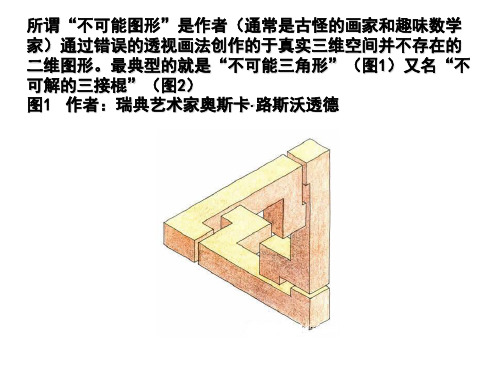
不可能图形
1958年美国的《心理学杂志》上，彭罗斯发表了他的不可解的三接棍.如图1-1.他称之为立体的矩形构造：三个直角并显示出垂直，但它是不可能存在于空间的，因为在这里三个直角似乎成了一个“三角形”，但三角形是平面而非立体的图形，三个内角和为180°，而非270°.
图1-1
20世纪50年代，罗格和彭罗斯写了论不可能图形的文章，文章描述了一种“没有尽头的楼梯”，踏着楼梯好像是一步一步地上升，然而楼梯都是停留在一个水平面上.如图1-2.
图1-2
荷兰著名画家埃舍尔被认为是20世纪公认的视错觉画大师.他
的作品以其深刻的数学、物理含义特别得到科学家的重视.如图1-3，他为第十届国际数学大会所作的会标，就是一个三维空间不可能的图形.
图1-3。

不可能立方体彭罗斯三角形彭罗斯三角形（Penrose triangle）第一次是被瑞典艺术家Oscar Reutersvärd创造出来，而后在20世纪50年代被数学家罗杰·彭罗斯（Roger Penrose）所推广。

其特点被以不可能图形为灵感来创作的艺术家埃舍尔（M. C. Escher）在其作品中很好地体现出来。

类似的图形还有彭罗斯正方形、彭罗斯五边形等。

彭罗斯三角形(2张)彭罗斯阶梯彭罗斯阶梯（Penrose Stairs），由莱昂内尔·彭罗斯（Lionel Penrose）和他的儿子罗杰·彭罗斯（Roger Penrose）创作。

是彭罗斯三角形的一个变式。

这是一个由二维图形的形式表现出来的拥有4个90°拐角的四边形楼梯。

由于它是个从不上升或下降的连续封闭循环图，所以一个人可以永进在上面走下去而不会升高。

显然这在三维空间中是不可能的。

[1]潘洛斯阶梯，又名潘罗斯阶梯、彭罗斯阶梯，由英国著名数学物理学家、牛津大学数学系名誉教授潘洛斯（Roger Penrose）提出。

潘洛斯阶梯是：四条楼梯，四角相连，但是每条楼梯都是向上的，因此可以无限延伸发展，是三维世界里需要在一定角度下才能看到的楼梯。

潘洛斯阶梯，曾出现在电影《盗梦空间》（Inception）里面的清醒梦境（lucid dream）中。

Arthur 展示给Ariadne看的奇怪阶梯，以及Arthur绕到佣兵背后的楼梯间，这是一座无限循环的阶梯。

这种不可能出现的物体来自于将三维物体描绘于二维平面时出现的错视现象。

其名称Penrose来自于英国数学物理学家罗杰·潘洛斯（Roger Penrose），他于1950年代设计了Penrose triangle，潘洛斯写了几篇文章讨论这些所谓的不可能事件，On the Cohomology of Impossible Figure这篇短文讨论了这些对象的群的上同调。