当前位置：文档之家 › 空间图形的基本关系的认识

空间图形的基本关系的认识

  • 格式：docx
  • 大小：173.77 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

4.1空间图形基本关系的认识

4.1空间图形基本关系的认识

c
b
B
记作： P
β
3. 空间两条直线的位置关系有三种：A
①平行直线—— 在同一个平面内，没有公 共点的两条直线。 ②相交直线—— 在同一个平面内，有且只有 一个公共点的两条直线。
α α
a
c
b
B
b 记作：a//b
a
β
a O b
记作： b O a
③异面直线— 不在任何一个平面内，没有公共点的两条直线。 —
b
α
b
a
a β b
α
γ
a
A （1）直线在平面内— 直线与平面有无数个 — 公共点。 （2）直线与平面相交— 直线与平面只 α 有一个公共点。 —
4. 空间直线与平面的位置关系有三种：
b
a
β
F
E
（3）直线与平面平行—— 直线与平面没有公共点。
5. 空间平面与平面的位置关系有两种：
（1）平行平面—— 没有公共点的两个平面。 （2）相交平面—— 两个平面不重合， 并且有公共点。 α
E
β
F
练习
1.思考题：
（1）没有公共点的两条直线叫做平行直线，对吗？ （2）空间两条没有公共点的直线叫做异面直线，对吗？
（3）分别在两个平面内的两条直线一定是异面直线吗？
（4）平面内一直线与这个平面外的一条直线一定是异面直线吗？
2.说出正方体中各对线段、线段与平面的位置关系： （1）AB和CC1； D1 （2）A1 C和BD1 ； B1 A1 （3）A1 A和CB1； （4）AC和A1 C1； （5）BC与平面A1 C1； （6）B1 C与平面AC； D （7）AB与平面AC。 A B
§4
实例分析

空间图形基本关系的认识

空间图形基本关系的认识
如果两条异面直线 a , b 所成的角为直 角，我们就称这两 条直线互相垂直 , 记为a ⊥ b
思考 : 这个角的大小与O点的位置有关吗 ? 即O点位
置不同时, 这一角的大小是否改变?
b′ b
a′ ″

O
例3
例4
如图，正方体ABCD-EFGH中,O为侧面ADHE的中心，求
(1)BE与CG所成的角？
B
C
解决问题
思想方法 : 平移转化成相交直线所成的角,即化空间图形问题为平面图形问题 异面直线所成角的定义: 如图,已知两条异面直线 a , b , 经过空间任一点O作 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角(或直角)叫做异面直线所成的角 (或夹角).
o o
异面直线所成的角的范围( 0 , 90 ]
异面直线所成的角
(1)复习回顾 在平面内,两条直线相交成四 个角, 其中不大于90度的角称为它 们的夹角, 用以刻画一条直线相对 另一条直线的倾斜程度, 如图. (2)问题提出 在空间,如图所示, 正方体 ABCD－EFGH中, 异面直线AB
O
H E F
G
相对于HF的倾斜程度可以怎样
来刻画呢?
D A
空间图形基本 关系的认识
必修2 第一章
立体几何初步
回顾：平面是无限延展的，我们见到的“平
面”只是数学里所说平面的一部分，通常用 平行四边形来表示平面. 平面通常用希腊字母α 、β 、γ 等来表 示，也可以用表示平行四边形的四个顶点或 两个相对顶点的字母来表示.(有三种表示） 例如：下图中平面α ，平面ABCD，平面 AC都表示同一个平面. A D
3.如图是一个正方体的展开图,如果将它还原为正方体, 那么 AB ,

高中数学第一章立体几何初步1.4空间图形的基本关系与公理1.4.1空间图形的基本关系与公理1公理3课

高中数学第一章立体几何初步1.4空间图形的基本关系与公理1.4.1空间图形的基本关系与公理1公理3课
与平面的位置关系. 如果一条直线和一个平面有无数个公共点,则称这条直线在这个 平面内.直线 l 在平面 α 内,记作 l⫋α. 如果一条直线和一个平面只有一个公共点,则称这条直线和这个 平面相交.直线 l 与平面 α 相交于点 P,记作 l∩α=P. 如果一条直线和一个平面没有公共点,则称这条直线和这个平面 平行.直线 l 与平面 α 平行,记作 l∥α. (5)空间平面与平面的位置关系. 如果两个平面没有公共点,则称这两个平面互相平行.平面 α 与平 面 β 平行,记作 α∥β. 如果两个平面不重合但有公共点,则称这两个平面相交.
问题导学
当堂检测
1.公理 1 的应用 活动与探究 例 1 已知 a∥b,a∩c=A,b∩c=B,求证:a,b,c 三条直线在同一 平面内. 思路分析:依题意,可先证 a 与 b 确定一个平面,再证明 c 在这个平 面内,从而可证 a,b,c 在同一平面内. 证明:∵ a ∥b , ∴ a 与 b 确定一个平面 α, ∵ a∩c=A,∴ A∈a,从而 A∈α; ∵ b∩c=B,∴ B∈b,从而 B∈α. 于是 AB⫋α,即 c⫋α,故 a,b,c 三条直线在同一平面内.
若 A∈α,A∈β,且 α,β 不重 合,则 α∩β=l,且 A∈l
目标导航
预习引导
预习交流 3
公理 1 的三个推论是什么? 提示:推论 1:一条直线和直线外一点确定一个平面. 推论 2:两条相交直线确定一个平面. 推论 3:两条平行直线确定一个平面.
预习交流 4
公理 1 中的“有且只有一个”的含义是什么? 提示:“有”是说图形存在,“只有一个”是说图形唯一.“有且只有”强 调的是存在性和唯一性两个方面,确定一个平面中的“确定”是“有且只 有”的同义词,也是指存在性和唯一性这两个方面.

【数学】1.4.1 空间图形基本关系的认识 课件 (北师大版必修2)

【数学】1.4.1 空间图形基本关系的认识 课件 (北师大版必修2)
第一章 立体几何初步
4.1 空间图形基本关系的认识
构成空间图形的基本元素
• 点是构成空间图形的最基本的元素
• 线可看作是具有某一特点的点的集合， 也是构成空间图形的元素 • 面也可视为无数点的集合，同时也是构 成空间图形的元素 • 它们之间有什么关系呢？
阅读课本实验分析
• • • • • 试思考以下问题 1、点和直线有什么关系？ 2、点和平面有什么关系？ 3、直线与直线有哪些关系？ 4、平面与平面有什么关系？
异面直线：不在任何一个平面内的两条直线， 作图时为了表示异面直线不共面的特点通 常用一个或两个平面来衬托
例 如图是一个正方体的展开图，如果将它还 原为正方体，那么AB、CD、EF、GH这四条 线段所在的直线是异面直线的有 __________对，分别是______________？
解：3对，分别是AB、GH；AB、CD；GH、EF。
空间直线与平面的位置关 系
空间平面与平面的位置关 系
• 空间平面与平面的位置关系：平行；相 交
ห้องสมุดไป่ตู้
空间点与线的关系
• 空间点与直线的位置关系有两种：
点 P 在直线 上：
点 P 在直线 外： ；
空间点与平面的关系
• 空间点与平面的位置关系有两种：
空间直线与直线的位置关 系
平行直线：在同一平面内但没有公共点的两条直线， 记作：a∥b 相交直线：在同一平面内有且只有一个公共点的两 条直线，记作a∩b=P

高中数学第一章立体几何初步4空间图形的基本关系与公理4.1空间图形基本关系的认识4.2空间图形的公理

高中数学第一章立体几何初步4空间图形的基本关系与公理4.1空间图形基本关系的认识4.2空间图形的公理
第十二页，共42页。
[小组合作型]
空间点、线、面的位置(wèi zhi)关系
(1)如果 a α，b α，l∩a＝A，l∩b＝B，l β，那么 α 与 β 的位置关系是________．
(2)如图 1-4-1，在正方体 ABCD-A′B′C′D′中， 哪几条棱所在的直线与直线 BC′是异面直线？
图 1-4-1
第十页，共42页。
两个平面若有三个公共点，则这两个平面( )
A．相交
B．重合
C．相交或重合
D．以上都不对
【解析】 若三个点在同一条直线上，则两平面可能相交；若这三个点不 在同一直线上，则这两个平面重合．
【答案】 C
第十一页，共42页。
[质疑·手记] 预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流： 疑问 1： _____________________________________________________ 解惑： _______________________________________________________ 疑问 2： _____________________________________________________ 解惑： _______________________________________________________ 疑问 3： ______________________________________________________ 解惑： _______________________________________________________
平面与平面 的位置关系
面面平行 面面相交
α∥β α∩β＝a
第五页，共42页。

空间图形的基本关系与公理(1)

空间图形的基本关系与公理(1)

分析 可先转换成符号语言，再作图．
解 (1)A∈α，B∈α，A∈l，B∈l
(2)l α，P∈l，P∈α.
(3)α∩β＝l，m α，m∥l.

变式训练
将下面用符号语言表示的关系改用文
字语言予以叙述，并且用图形语言予以表示．
解 文字语言叙述为： 点 A 在平面 α 与平面 β 的交线 l 上，AB、AC 分 别在 α、β 内． 图形语言表示为如图所示．
B α


A
（2）点在平面外
记作：
B
空间两条直线的位置关系有三种：
①平行直线——
在同一个平面内，没有公共点的两条直线.
②相交直线—— 在同一个平面内，有且只有一个公共点的两
条直线.
记作：a//b a b α
b
记作： β
ab O
a O b b
③异面直线——不同在任何一个平面内
α a
a
β b

④若直线 a∥直线 b，b α，那么直线 a 平行于平面α内的
变式训练
下面命题中正确的个数是
( C )
①如果 a、b 是两条直线，a∥b，那么 a 平行于经过 b 的任何一个平面； ②如果直线 a 满足 a∥α，那么 a 与平面α内的任何 一条直线平行； ③如果直线 a、b 满足 a∥α，b∥α，则 a∥b； ④如果直线 a、 和平面α满足 a∥b， α， α， b a∥ b 那么 b∥α； ⑤如果 a 与平面α上的无数条直线平行，那么直线 a 必平行于平面α. A．0 B．2 C．1 D．3
解析
A、B 都不能保证 α、β 无公共点，如图 1
所示；C 中当 a∥α，a∥β 时 α 与 β 可能相交，如 图 2 所示；只有 D 说明 α、β 一定无公共点．

1.4.1 空间图形基本关系的认识与公理1~3 课件(北师大必修2)


[通一类] 1．已知a∥b∥c，l∩a＝A，l∩b＝B，l∩c＝C，求证： 直线a，b，c和l共面．
证明：∵a∥b，∴直线a与b确定一个平面，设为α ，
∵l∩a＝A，l∩b＝B， ∴A∈a，B∈b，则A∈α ，B∈α . 而A∈l，B∈l， ∴由公理1可知：lα . Þ ∵b∥c，∴直线b与c确定一个平面，设为β ， 同理可知lβ . Þ
Þ ∴A∈α ，B∈α ，∴ABα . Þ 即aα ，
∵b∥c，∴直线b与c确定
∴a，b，c三线共面．
[悟一法]
证明点线共面的常用方法：
①纳入平面法：先确定一个平面，再证明有关点、线 在此平面内． ②辅助平面法：先证明有关的点、线确定平面α ，再 证明其余元素确定平面β ，最后证明平面α 、β 重合．
[通一ห้องสมุดไป่ตู้] 2．如图，在正方体ABCD－A1B1C1D1中，设线段
A1C与平面ABC1D1交于Q，求证：B，Q，D1三点共线．
证明：∵D1∈平面ABC1D1，
D1∈平面A1D1CB，
B∈平面ABC1D1， B∈平面A1D1CB，
∴平面ABC1D1∩平面A1D1CB＝BD1. ∵A1C∩平面ABC1D1＝Q，
[读教材·填要点]
一、空间图形的基本位置关系
点在直线上 点与直线 点在直线外 (1)点 点在平面内 点与平面点在平面外
(2)空间两条直线的位置关系. 位置关系 相交直线 共面情况 在同一个平面内 公共点个数 1个 没有 没有
平行直线
异面直线
在同一个平面内
[错因]
在证明共面问题时，必须注意平面是确
定的．上述错解中， 由于没有注意到B，C，D三点不 一定确定平面，即默认了B，C，D三点一定不共线， 因而出错．也即题知条件由B，C，D三点不一定确定 平面，因此就使得五点的共面失去了基础．

高中数学-8.3 空间图形的基本关系与公理

知识梳理 知识梳理 双击自测 核心考点 学科素养
考纲要求
-3-
1.空间图形的公理 (1)公理1:过不在同一条直线上的三点,有且只有一个平面(即可 以确定一个平面). 推论1:经过一条直线和这条直线外一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面. (2)公理2:如果一条直线上的两点在一个平面内,那么这条直线上 所有的点都在这个平面内(即直线在平面内). (3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只 有一条过这个点的公共直线. (4)公理4:平行于同一条直线的两条直线平行.
考点1 考点2 考点3
8.3
空间图形的基本关系与公理
知识梳理 双击自测 核心考点 核心考点 学科素养
考纲要求
-18-
知识方法
易错易混
对点训练2 (1)如图,G,N,M,H分别是三棱柱的顶点或所在棱的 中点,则直线GH,MN是异面直线的图形有 .(填上所有正 确答案的序号)
关闭
题图①中,直线GH∥MN; 题图②中,G,H,N三点共面,但M∉平面GHN,因此直线GH与MN异面; 题图③中,连接MG,GM∥HN, 因此GH与MN共面; 题图④中,G,M,N共面,但H∉平面GMN,因此GH与MN异面.
解析
答案
第八章 1 2 3 4 5
8.3
空间图形的基本关系与公理
知识梳理 双击自测 双击自测 核心考点 学科素养
考纲要求
-11-
自测点评 1.做有关平面基本性质的判断题时,要抓住关键词,如“有且只 有”“只能”“最多”等. 2.两个不重合的平面只要有一个公共点,那么两个平面一定相交 且得到的是一条直线. 3.异面直线是指不同在任何一个平面内,没有公共点的直线.不能 错误地理解为不在某一个平面内的两条直线就是异面直线.

空间几何的相交和平行关系

空间几何的相交和平行关系空间几何是研究三维形体的相对位置和关系的学科，而其中最基本和重要的概念之一就是相交和平行关系。

在本文中，我们将探讨这两个概念的含义以及它们在空间几何中的应用。

1. 相交关系相交关系是指两个或多个图形在空间中有交集的情况。

具体来说，当两个或多个图形的部分或全部相互穿越时，我们可以说它们相交。

在空间几何中，常见的相交关系有以下几种：1) 点与直线的相交：当一条直线与一个点相交，即该点在直线上，我们可以说点与直线相交。

2) 点与平面的相交：当一个点与一个平面相交，即该点在平面上，我们可以说点与平面相交。

3) 直线与直线的相交：当两条直线在空间中有一个公共点时，我们可以说它们相交。

4) 直线与平面的相交：当一条直线与一个平面有一个公共点时，我们可以说它们相交。

5) 平面与平面的相交：当两个平面在空间中有一条直线作为它们的交集时，我们可以说它们相交。

相交关系在几何推理和几何证明中起着重要的作用。

通过分析图形的相交关系，我们可以得出很多有用的结论和性质，进而解决问题。

2. 平行关系平行关系是指两个或多个图形在空间中没有交集的情况。

具体来说，当两个或多个图形的部分或全部没有交点时，我们可以说它们平行。

在空间几何中，常见的平行关系有以下几种：1) 直线与直线的平行：当两条直线在空间中没有交点，且它们的方向相同或重合时，我们可以说它们平行。

2) 直线与平面的平行：当一条直线与一个平面没有交点，且这条直线在这个平面上的任意一条平行线上时，我们可以说它们平行。

3) 平面与平面的平行：当两个平面没有交集，且它们的法向量平行时，我们可以说它们平行。

平行关系在几何推理和几何证明中也是非常重要的。

通过研究图形的平行性质，我们可以得出很多结论和性质，从而解决各种实际问题。

总结：空间几何中的相交和平行关系是非常基础且重要的概念。

相交关系指的是两个或多个图形在空间中有交集，而平行关系指的是两个或多个图形在空间中没有交集。

空间图形的基本关系

•平行平面
//
两个平面没有公共点
平面 与平面 平行


•相交平面
两个平面有公共点

平面 与平面 相交于直线 l
l
l

预习自测
例1、如图所示，下列符号表示错误的是 A. l B. P l P C. l D. P （ A）
l
例2、如图所示，在这个正方体中， BM与ED平行； CN与BM是异面直线； CN与BE是异面直线； DN与BM是异面直线. 以上四个命题中，正确命题的序号是
m
（1）


P
l
A
（2）

l

Q
（3）

m
l

n
3、“a , b 是异面直线”是指： a b 且a 不平行于b ； b 平面 且 a b ； a 平面 ， b 平面 ； a 平面 ， 不存在平面 ，能使 a 且 b 成立. 上述结论中，正确的是 （ C ） A. B. C. D.
b a
b
a A
•异面直线（两条直线不同在任何一个平面内，无交点） 直线a与b异 面
b
b
a
a
4、空间直线与平面的位置关系有三种:
•直线在平面内 直线a 在平面 内

b
a
a
•直线与平面相交 直线b与平面 相交


B
b B
•直线与平面平行
直线c与平面 平行 c //
c

5、空间平面与平面的位置关系有二种:
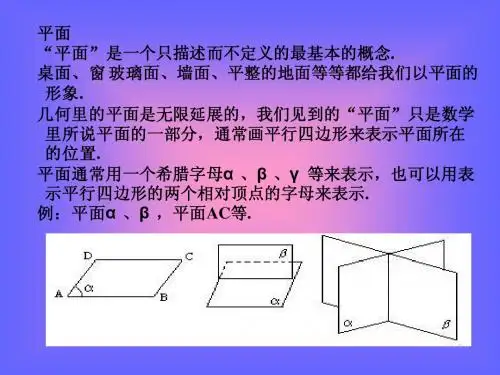
§4.1空间图形基本 关系的认识
教学目标
掌握空间图形的基本构成 点、线、面 的五种基本位置关系；（重点） 理解异面直线的概念；（难点） 掌握文字语言，符号语言，图形语言的相 互转化.（难点）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

空间图形的基本关系的认识
【学习目标】
1.通过长方体这一常见的空间图形，了解空间中点、线、面的基本位置关系，并会用符号语言进行表述。

2.掌握空间图形的公理1、2。

【学习重点】
以长方体为载体，直观认识和理解空间点、线、面之间的位置关系，加强符号语言的运用能力和推理论证能力。

【学习难点】
异面直线的理解，公理1、2的应用。

【课前预习案】
关于异面直线 （1）若直线α,b 是异面直线，则在空间中找不到一个平面，使其同时经过
这两条直线.
（2）不可以误解为分别在不同平面的两条直线.
（3）异面直线既不平行又不相交.
（4）直线a 交平面α于点A ，直线b 在平面α内且不过点A,则直线α,b 异
面.
符号语言
若A l ,B l ,A ∈α,
B α∈,则__________.
_________.
1 个平面内，那么这条直线上
________都在这
个平面内（即直
线__________）. 公 理 2 经过__________
上的三点，有且
_____一个平面
（即可以确定一
个平面）.
若A 、B 、C 三点不共线，则____________一个平面α使A α∈，B α∈，C α∈.
【课堂探究案】
学法指导：根据题意画出直观图，利用直观图分析点、线、面之间的位置关
系。

1.用符号语言表示下列语句，并画出图形
（1）直线 经过平面α内两点A 、B
（2）直线 在平面α外，且经过平面α内一点P
（3）直线 是平面α与平面β的交线，平面α内有一条直线m 与 平行
2.如图，在三棱锥S —ABC 的六条棱所在的直线中，异面直线共有（ ）
A.2对
B.3对
C.4对
D.6对
3.若直线m α平面⋂=P ，则下列结论中正确的是（ ）
A.平面α
内的所有直线与直线m 异面 B.平面α
内不存在与直线m 平行的直线 C.平面α
内存在唯一的直线与m 平行 D.平面α内的所有直线与直线m 相交 4.如图在长方体1111ABCD A B C D -所有棱中
（1）与11B A 异面的直线有_________________
（2）与1BD 异面的直线有_________________
（3）与11B A 平行的直线有_________________
（4）与11B A 相交的直线有_________________ 探究：思考并举例说明
（1）经过一条直线和这条直线外一点，可以确定一个平面吗？
（2）经过两条相交直线，可以确定一个平面吗？
（3）经过两条平行直线，可以确定一个平面吗？
5.下列命题正确的是 （ ）
A B C
S A B C
D
A ．过两条直线有且只有一个平面 ；
B.过一点和一条直线有且只有一个平面；
C.过梯形两腰所在的直线有且只有一个平面；
D.过三点有且只有一个平面。

6.两个平面重合的条件是 （ ）
A.有两个公共点；
B.有无数个公共点；
C.有不共线的三个公共点；
D.有一条公共直线；
【课后检测案】
1.如图所示，正方体1111ABCD A B C D 中，M 、N 分别是1111A B B C 和的中点. .
（1）用符号语言表示：①点A 与直线CN 、AB 的关系；②点M 与面1111A B C D 、面ABCD 的关
系；③直线MN 与11A C 、CN 的关系；④MN 与面1111A B C D 、面ABCD 、面11BB C C ；⑤面ACMN
与面ABCD 、面1111A B C D 与面ABCD
（2）AM 和CN 是否是异面直线？
（3）11D B 和CC 是否是异面直线？
说明理由.
2.下列说法中正确的个数是 （ ） ①铺得很平的一张白纸是一个平面; ②可以画一个长20m , 宽30m 的平面;
③通常300页的书要比10页的书厚一些, 那么300个平面重合在一起时一定比
10个平面重合在一起厚.
A. 0个
B. 1个
C. 2个
D. 3个
3. 空间四点A 、B 、C 、D 共面而不共线, 那么这四点中（ ）
A.必有三点共线
B.必有三点不共线
C.至少有三点共线
D.不可能有三点共线。