不同水力过渡数学模型的计算精度分析
- 格式:pdf
- 大小:722.53 KB
- 文档页数:5


水力过渡过程计算嘿,朋友!咱们今天来聊聊水力过渡过程计算这回事儿。
你知道吗,水力过渡过程就像是一场水流的大冒险!想象一下,水在管道里、渠道中奔跑,突然遇到了一些状况,比如阀门关闭、水泵启动或者管道破裂。
这时候,水的流动状态可就发生了巨大的变化,就像一个调皮的孩子突然改变了玩耍的方式。
水力过渡过程计算,那可是相当重要的!比如说,在城市的供水系统中,如果不进行准确的计算,一旦出现紧急情况,比如突然停水或者水压骤变,那可就麻烦大啦!家里的水龙头可能不出水,洗澡洗到一半变成冷水澡,这得多难受啊!水力过渡过程计算其实就像是给水流规划路线。
我们要考虑水的速度、压力、流量这些因素,就像给一个旅行团安排行程,要考虑路程、时间和费用一样。
如果计算不准确,水流就可能“迷路”,造成各种问题。
比如说,在水电站中,水轮机的调节如果没有基于准确的水力过渡过程计算,那电力供应可能就会不稳定,一会儿亮堂堂,一会儿黑黢黢,这可咋整?再看看长距离的输水管道,如果不精心计算水力过渡过程,管道可能承受不住压力,出现破裂,那水就像脱缰的野马一样四处乱跑,这得造成多大的损失啊!那怎么进行水力过渡过程计算呢?这可不是拍拍脑袋就能搞定的。
得有专业的知识和工具。
就像厨师做菜要有好的食材和刀具一样。
我们要建立复杂的数学模型,把水流的各种特性都考虑进去。
这可不容易,就跟拼图一样,一块一块地拼凑,直到呈现出完整清晰的画面。
而且,还得根据实际情况不断调整参数,这就好比裁缝给人做衣服,得量体裁衣,不断修改,才能合身。
计算过程中,每一个数据都不能马虎,一个小差错可能就会导致整个结果大错特错,这难道不就像下棋走错一步满盘皆输吗?总之,水力过渡过程计算可不是一件轻松的事儿,但它又极其重要。
只有把这个计算做好了,我们的水利工程才能稳定运行,为我们的生活带来便利,不是吗?。
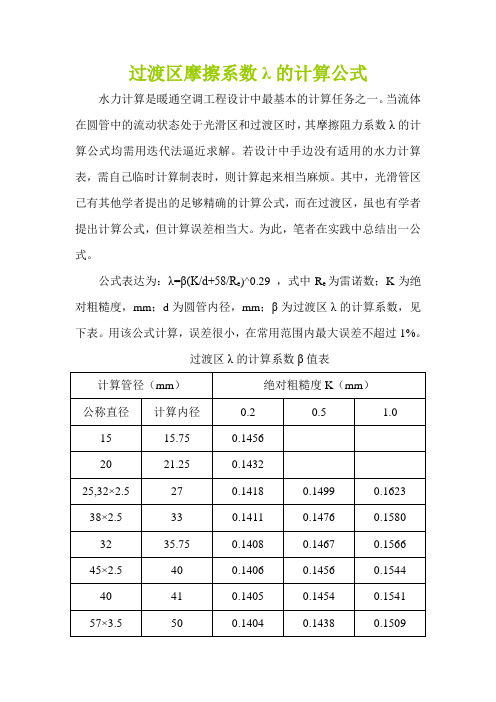
过渡区摩擦系数λ的计算公式水力计算是暖通空调工程设计中最基本的计算任务之一。
当流体在圆管中的流动状态处于光滑区和过渡区时,其摩擦阻力系数λ的计算公式均需用迭代法逼近求解。
若设计中手边没有适用的水力计算表,需自己临时计算制表时,则计算起来相当麻烦。
其中,光滑管区已有其他学者提出的足够精确的计算公式,而在过渡区,虽也有学者提出计算公式,但计算误差相当大。
为此,笔者在实践中总结出一公式。
公式表达为:λ=β(K/d+58/R e)^0.29 ,式中R e为雷诺数;K为绝对粗糙度,mm;d为圆管内径,mm;β为过渡区λ的计算系数,见下表。
用该公式计算,误差很小,在常用范围内最大误差不超过1%。
过渡区λ的计算系数β值表此表完成于2003年3月11日星期二下午6时52分,从而使用Excell进行采暖水力计算速度和准确性达到了一个新水平。
PPR,PE-X,PAP三种不同塑料管材的沿程损失计算经过实际测试塑料管中的沿程损失理论计算公式与实际有明显的差距,具体分析如下:由于管材原材料差别及制造工艺不同所致。
铝塑复合管的内壁材料一般是聚乙烯(PE),或交联聚乙烯(PE-X),与交联聚乙烯(PE-X)管的材质相近或相同,水力条件也相近,故水头损失也相近并均大于理论计算值,而PP-R管是以聚丙烯(PP)和1%~7%的乙烯为原料,采用气相共聚法均匀聚合而成,其水力条件比PE-X和PAP更优,因此,水头损失小于理论计算值。
各修正系数如下:对于PE-X和PAP管的沿程水头损失计算时,乘以1.12的修正系数。
对于PP-R管的沿程水头损失计算时,乘以0.947的修正系数。
另通过试验证实PE-X ,PAP和PP-R管的沿程水头损失比钢管的沿程水头损失小得多,流速越大水头损失减少的幅度也越大。
此数据取自《给水排水》-2003-8期。
另本期还有大空间的《南京国际展览中心》消防给水设计的有关高大空间用雨淋系统的介绍。

水文及水力学数学模型摘要:在二维水流数学模型的基础上,研究开发了将模型区内的陆面区和水面区的产汇流与模型区入流洪水演进有机结合的水文水力学模型。
该模型采用全区水域智能自动跟踪识别技术,解决了模型区内交替出现的陆域与水域的区分问题顺此基础上考虑了模型区内水面区与陆面区的产、汇流特征,提出了处理模型区产汇流问题一种行之有效的方法,提高了模拟计算的精度。
通过对南水北调中线总干渠左岸区域洪水的数值模拟,结果表明,计算值与实测调查值吻合较好,具有较高的计算精度。
关键词:产流;汇流;洪水;水文水力学模型二维水流数学模型在水利水电工程的规划、设计及管理中,作为复演、再现和预测洪水传播和洪水演进的历史、现状和将来是目前极为重要的技术手段。
但是以往的二维水流数学模型仅考虑了洪水演进,模拟计算时不但将目标位置的洪水过程直接移至模型上边界作为模型的入流,人为把模型区内降雨所产生的洪水提到了模型区以上,使目标位置的洪水过程发生了变化,更重要的是它忽略了模型区的产流和汇流因素。
对于平原区的洪水演进,特别是模型区相对于整个流域面积比重较大且有频繁交替的陆面区和水面区时,模拟计算的结果就很难反映客观实际。
在南水北调中线总干渠左岸防洪水位课题研究中,研究开发了将模型区域的产汇流与河沟洪水演进有机结合的水文、水力学模型。
1区域工程情况南水北调中线工程属于特大型长距离调水工程,途径河北省太行山前的平原区,各交叉河道的防洪水位不仅是建筑物设计的依据,也是总干渠左岸堤顶防洪设计的依据。
在南水北调交叉河流中,部分小型河沟发育较差,遇大洪水就漫溢出槽,呈坡面流状态,有时数条河流串在一起,洪水期河流的界限不清,各河水流相互影响,形成典型的洪水串流区,特别是南水北调总干渠建成后,总干渠对左岸的坡面流形成阻挡作用,使左岸洪水的淹没范围和水深有所增加,进一步加剧了该区河流洪水的串流情势。
在这种情况下一维水流数学模型很难满足设计需要,而必须借助于二维水流数学模型。


大波动过渡过程计算分析总结水电站输水系统和机组过渡过程的计算分析具有重要的意义,该计算分析对于机组参数GD2的选择、导叶关闭规律的确定、调压室参数的选择和管道线路的布置等方面都有重要的指导作用。
水电站过渡过程计算分析由大波动过渡过程计算分析和小波动过渡过程计算分析两部分组成。
以下对大波动过渡过程计算分析进行总结说明。
大波动过渡过程计算分析主要包含以下几个部分:①该类系统数学计算模型的建立和求解;②仿真计算程序的编制;③具体输水系统有关原始数据的准备(包含实际系统概化问题);④各种大波动控制工况的计算分析;⑤《水力过渡过程计算分析报告》的撰写。
一.数学计算模型的建立水电站输水系统数学模型由输水道数学模型和边界数学模型两部分构成。
1.输水道数学模型目前,输水道数学模型是根据一元总流流体的运动方程和连续方程,建立有压管道水力瞬变的弹性水锤基本方程组,然后利用特征线法对方程组进行简化、求解(这里暂不讨论无压输水道);由于在建立和求解模型的过程中,存在一些简化和假定条件,因此存在以下几个值得研究的问题:①现模型采用一元流假定,该假定在某些情况下不适用,应该改用“二元流”或“三元流”原理构造数模。
②该模型要求“同一段管道为单特性管”,因此须对非单特性管进行合理概化。
③该模型中管道阻力系数采用的是阀门关闭前稳态流动的值,实际应该采用动态的阻力系数。
④计算时间步长和波速调整的优化。
⑤含气水锤模型的建立。
2.边界数学模型不同边界具有不同的数学模型,目前基本边界的数学模型已较成熟,满足仿真计算精度要求。
3.数模的求解方法有压输水道数学模型采用特征线法求解;简单边界数学模型(如一元非线性代数方程)采用改进的不动点迭代法求解;复杂边界数学模型(如二元非线性代数方程组)采用牛顿-莱甫生法求解。
二.仿真计算程序的编制利用FORTRAN语言将已建立的数学模型和所选的求解方法编制成仿真计算程序。
同时,须注意以下几个问题:①水轮机特性曲线的变换(目前采用改进的Suter法)。
供水工程水力过渡过程分析及运行安全评估今天,我们来探讨一下关于供水工程水力过渡过程分析及运行安全评估的问题。
水力过渡过程是指当水流动速度发生改变时,水在管道内通过过渡段的一段时间内,流速,流向及流量等参数的多次变化过程。
在供水工程的设计和施工阶段,水力过渡过程的分析非常重要。
因为,在过渡段内,水流的速度、方向、压力等参数的变化可能对管道、水泵、阀门等设备造成损害,从而导致运行安全上的问题。
同时,管道内可能还存在气穴、沉淀物或水中的杂质等物质,这些物质会影响水的流动和水质的清洁,进一步影响供水工程的正常运行和使用。
为了保障供水工程的设计和运行安全,水力过渡过程应被仔细分析和评估,确定有关的参数,然后再进行合理的管道尺寸和附属设备的选型和设计。
在供水工程的运行阶段,我们还应该对供水工程的运行安全进行评估。
评估的内容应该包括管道、设备运行的情况,水质等方面的情况。
当然,评估还必须根据各地的不同特点,选择合适的评估方法和工具,以确保评估结果的准确性。
在评估过程中,我们应该关注以下几个重点:1、管道材质和尺寸是否合理,是否符合设计要求。
2、设备的运转是否正常,压力和流量是否稳定,油温和振动是否过高。
3、水质是否达标,是否存在水中杂质、气穴和沉淀物等问题。
4、水力过渡过程是否合理,是否存在过大的压力和速度梯度,是否存在过多的涡流和水锤。
5、是否发现任何安全隐患或生产事故,是否进行了及时修复和整改。
通过对以上问题的分析和评估,可以帮助我们了解供水工程的运行情况和安全状况,并及时提出改进和优化措施。
因此,我们需要根据供水工程的实际情况,设计合理的评估方案,并整合各种可以获取的实验数据和实测数据,以确保评价结果的可靠性和实用性。
总之,对于供水工程来说,水力过渡过程和运行安全评估是一个十分重要和复杂的问题。
要做好这项工作,需要综合考虑各种因素和条件,量化分析和定量评估,以确保供水工程的正常运行和使用。
大波动过渡过程计算分析总结水电站输水系统和机组过渡过程的计算分析具有重要的意义,该计算分析对于机组参数GD2的选择、导叶关闭规律的确定、调压室参数的选择和管道线路的布置等方面都有重要的指导作用。
水电站过渡过程计算分析由大波动过渡过程计算分析和小波动过渡过程计算分析两部分组成。
以下对大波动过渡过程计算分析进行总结说明。
大波动过渡过程计算分析主要包含以下几个部分:①该类系统数学计算模型的建立和求解;②仿真计算程序的编制;③具体输水系统有关原始数据的准备(包含实际系统概化问题);④各种大波动控制工况的计算分析;⑤《水力过渡过程计算分析报告》的撰写。
一.数学计算模型的建立水电站输水系统数学模型由输水道数学模型和边界数学模型两部分构成。
1.输水道数学模型目前,输水道数学模型是根据一元总流流体的运动方程和连续方程,建立有压管道水力瞬变的弹性水锤基本方程组,然后利用特征线法对方程组进行简化、求解(这里暂不讨论无压输水道);由于在建立和求解模型的过程中,存在一些简化和假定条件,因此存在以下几个值得研究的问题:①现模型采用一元流假定,该假定在某些情况下不适用,应该改用“二元流”或“三元流”原理构造数模。
②该模型要求“同一段管道为单特性管”,因此须对非单特性管进行合理概化。
③该模型中管道阻力系数采用的是阀门关闭前稳态流动的值,实际应该采用动态的阻力系数。
④计算时间步长和波速调整的优化。
⑤含气水锤模型的建立。
2.边界数学模型不同边界具有不同的数学模型,目前基本边界的数学模型已较成熟,满足仿真计算精度要求。
3.数模的求解方法有压输水道数学模型采用特征线法求解;简单边界数学模型(如一元非线性代数方程)采用改进的不动点迭代法求解;复杂边界数学模型(如二元非线性代数方程组)采用牛顿-莱甫生法求解。
二.仿真计算程序的编制利用FORTRAN语言将已建立的数学模型和所选的求解方法编制成仿真计算程序。
同时,须注意以下几个问题:①水轮机特性曲线的变换(目前采用改进的Suter法)。