实现预定轨迹的平面四连杆机构的优化设计

契贝谢夫四连杆机构的优化设计与应用
契贝谢夫四连杆机构是一种常用的机构，其由四根连杆和一个滑块组成。

契贝谢夫四连杆机构的优化设计和应用可以涉及以下方面：
1. 运动学分析和优化设计：可以通过对契贝谢夫四连杆机构的运动学特性进行分析和优化设计，以提高机构的性能。

通过优化连杆的长度和角度，可以实现所需的运动轨迹和位移，并最小化驱动力和摩擦损失。

2. 动力学分析和优化设计：可以通过对契贝谢夫四连杆机构的动力学特性进行分析和优化设计，以实现所需的力学性能。

通过优化连杆的惯量和刚度，可以提高机构的响应速度和精度，并最大限度地减小振动和动态载荷。

3. 结构强度分析和优化设计：可以通过对契贝谢夫四连杆机构的结构强度进行分析和优化设计，以确保机构在工作过程中的安全和可靠性。

通过优化连杆的剖面和材料，可以提高机构的承载能力和抗疲劳性，以应对不同工况和环境的要求。

4. 仿真和测试分析：可以通过使用计算机辅助设计和仿真软件，对契贝谢夫四连杆机构进行仿真分析，并验证优化设计的有效性。

同时，可以进行实际测试和试验，以验证优化设计参数和模型的准确性和可行性。

契贝谢夫四连杆机构在工程上有广泛的应用，例如在机械工程中可以应用于机器人、汽车发动机、传输机器和减速器等领域。

在机械设计和制造过程中，优化设计和应用契贝谢夫四连杆机构可以提高机械系统的性能、效率和可靠性。

此外，契贝谢夫四连杆机构也可以应用于模拟和教学实验，用于解决实际问题和培养学生的设计和创新能力。

平面连杆机构优化设计一、问题描述平面连杆机构是由所有构件均由低副连接而成的机构，四杆机构是最常用的平面连杆机构。

一般情况下，四杆机构只能近似实现给定的运动规律或运动轨迹，精确设计较为复杂。

在四杆机构中，若两连架杆中的一个是曲柄，另一个是摇杆，则该机构为曲柄摇杆机构。

曲柄摇杆机构可将曲柄的连续转动转变为摇杆的往复摆动。

设计一曲柄摇杆机构(如图1所示)。

已知曲柄长度l 1=100mm ，机架长度l 4=500mm 。

摇杆处于右极限位置时，曲柄与机架的夹角为φ0，摇杆与机架的夹角为ψ0。

在曲柄转角φ从φ0匀速增至φ0+90°的过程中，要求摇杆转角()200π32ϕϕψψ-+=。

为防止从动件卡死，连杆与摇杆的夹角γ只允许在45°~135°范围内变化。

图1 机构运动简图二、基本思路四杆机构的设计要求可归纳为三类，即满足预定的连杆位置要求、满足预定的运动规律要求、满足预定的轨迹要求。

本案例中，要求曲柄作等速转动时，摇杆的转角满足预定运动规律()00E π32ϕϕψψ-+=。

优化设计时，通常无精确解，一般采用数值方法得到近似解。

本案例将机构预定的运动规律与实际运动规律观测量之间的偏差最小设为目标，由此建立优化设计数学模型，并运用MATLAB 优化工具箱的相关函数进行求解。

三、要点分析优化设计数学模型的三要素包括设计变量、目标函数和约束条件。

依次确定三要素后，编写程序进行计算。

1.设计变量的确定通常将机构中的各杆长度，以及摇杆按预定运动规律运动时，曲柄所处的初始位置角φ0列为设计变量，即T04321T 54321)()(ϕl l l l x x x x x ==X (1)考虑到机构各杆长按比例变化时，不会改变其运动规律，因此在计算可取l 1为单位长度，而其他杆长则按比例取为l 1的倍数。

若曲柄的初始位置对应摇杆的右极限位置，则φ0及ψ0均为杆长的函数，即42123242210)(2)(cos arc l l l l l l l +-++=ϕ (2)43232422102)(cos arc l l l l l l --+=ψ (3)因此，设计变量缩减为3个独立变量，即T432T 321)()(l l l x x x ==X (4)2.目标函数的建立以机构预定的运动规律观测量ψE i 与实际运动规律观测量ψi 之间的偏差平方和最小为指标来建立目标函数，即min )()(12E →-=∑=mi i i f ψψX (5)式中，m 为输入角的等分数；ψE i 为预期输出角，ψE i=ψE (φi )；ψi 为实际输出角。

平面连杆机构的优化设计【教学目标】1.了解连杆机构优化设计的一般步骤2.掌握连杆机构优化设计的方法【教学重点】1.掌握连杆机构优化设计的方法【教学难点】1.掌握连杆机构优化设计的方法【教学准备】多媒体课件、直尺、圆规。

【教学过程】一、以工程实际案例引入课题实例1：飞机起落架（结合最近美国波音飞机频繁失事的新闻）实例2：汽车雨刮器说明：平面连杆机构的实用在生产生活中随处可见，是机械设计当中常见的一种机构。

二、定义回顾【提问】平面四杆机构的基本形式有哪些？【预设】机械原理是本科第四学期的课程，学生可能记不全，要引导性地带大家回忆。

【答案】曲柄摇杆机构、双曲柄机构、双摇杆机构三、回顾以前所学习的连杆机构设计方法，对比引入优化设计。

新课教授一、曲柄摇杆机构再现已知运动规律的优化设计1.设计变量的确定决定机构尺寸的各杆长度，以及当摇杆按已知运动规律开始运动时，曲柄所处的位置角φ0 为设计变量。

[][]1234512340T T x x x x x x l l l l ϕ== 考虑到机构的杆长按比例变化时，不会改变其运动规律，因此在计算时常l 1=1 ，而其他杆长按比例取为l 1 的倍数。

()()22212430124arccos 2l l l l l l l ϕ⎡⎤++-=⎢⎥+⎢⎥⎣⎦()221243034arccos 2l l l l l l ψ⎡⎤+--=⎢⎥⎢⎥⎣⎦经分析后，只有三个变量为独立的：[][]123234T T x x x x l l l ==2.目标函数的建立 目标函数可根据已知的运动规律与机构实际运动规律之间的偏差最小为指标来建立，即()()21minm Ei i i f x ψψ==-→∑3.约束条件的确定1）曲柄摇杆机构满足曲柄存在的条件()()()()()()1122133144143251234613240g x l l g x l l g x l l g x l l l l g x l l l l g x l l l l =-≤=-≤=-≤=+--≤=+--≤=+--≤六、课堂小结（板书）通过曲柄摇杆机构的优化设计，更深层的体会了优化设计数学模型的步骤：1.设计变量的确定。

平面连杆机构优化设计一、问题描述平面连杆机构是由所有构件均由低副连接而成的机构，四杆机构是最常用的平面连杆机构。

一般情况下，四杆机构只能近似实现给定的运动规律或运动轨迹，精确设计较为复杂。

在四杆机构中，若两连架杆中的一个是曲柄，另一个是摇杆，则该机构为曲柄摇杆机构。

曲柄摇杆机构可将曲柄的连续转动转变为摇杆的往复摆动。

设计一曲柄摇杆机构（如图1所示）。

已知曲柄长度l=100mm,机架长1度l4=500mm。

摇杆处于右极限位置时，曲柄与机架的夹角为80,摇杆与机架的夹角为十0。

在曲柄转角8从8 0匀速增至80+90°的过程中，要求摇杆转角甲=甲+二%-①1。

为防止从动件卡死，连杆与摇杆的夹角Y只0 3n 0允许在45°~135°范围内变化。

图1 机构运动简图二、基本思路四杆机构的设计要求可归纳为三类，即满足预定的连杆位置要求、满足预定的运动规律要求、满足预定的轨迹要求。

本案例中，要求曲柄作等2%-中)。

优化设计速转动时，摇杆的转角满足预定运动规律w =w +E 0 3n 0时，通常无精确解，一般采用数值方法得到近似解。

本案例将机构预定的运动规律与实际运动规律观测量之间的偏差最小设为目标，由此建立优化设计数学模型，并运用MATLAB优化工具箱的相关函数进行求解。

三、要点分析优化设计数学模型的三要素包括设计变量、目标函数和约束条件。

依次确定三要素后，编写程序进行计算。

1.设计变量的确定通常将机构中的各杆长度，以及摇杆按预定运动规律运动时，曲柄所处的初始位置角0列为设计变量，即X = (XX X X X)T = (l l l l①)T (1) 考虑到机构各杆长按比例变化时，不会改变其运动规律，因此在计算可取11为单位长度，而其他杆长则按比例取为11的倍数。

若曲柄的初始位置对应摇杆的右极限位置，则80及十0均为杆长的函数，即(l + l)2 + l2—12 /Q\①=arccos 12 43 (2)0 2(l1 + l2)l4(l + l )2—l2—l2 =arccos -4——2 4 3-因此，设计变量缩减为3个独立变量，即2l314X = (x1 x 2 x 3)T = (12 13l 4)T ⑷2.目标函数的建立以机构预定的运动规律观测量^ E i与实际运动规律观测量^ i之间的偏差平方和最小为指标来建立目标函数，即f (X) = X 皿-V )2 . min ⑸E i ii=1式中，m为输入角的等分数；（p E i为预期输出角，匕i W E（W i）；中i为实际输出角。

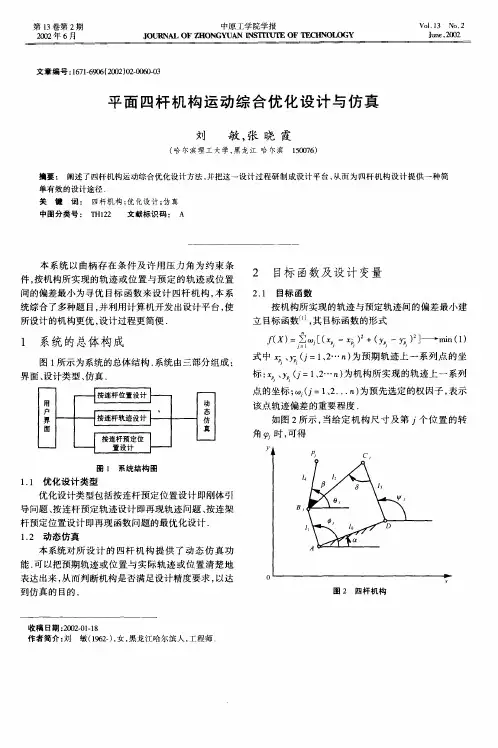
平面四杆机构的运动设计方案南阳高级技工学校—孔琳平面连杆机构中结构最简单，应用最广泛的是四杆机构，它是由四个构件通过低副连接组成的平面连杆机构，故称为平面四杆机构。

平面四杆机构是组成其他多杆机构的基础一、平面连杆机构的应用平面连杆机构能够实现多种运动轨迹曲线和运动规律。

在平面连杆机构中，所有的运动副均为低副。

因此，平面连杆机构又称为平面低副机构。

由于组成低副的两个构件之间是面接触，在承受相同的荷载时，其承载能力较大，耐磨损；再加上构件的形状简单，制造简便，易于获得较高的制造精度。

因此，平面连杆机构广泛地用于各种机械和仪器中。

但是，由于平面连杆机构的运动链较长，构件数和运动副数较多，而且在低副中存在间隙，所以会引起较大的运动积累误差，从而影响其运动精度。

而且平面连杆机构的设计比较复杂，通常难以精确地实现复杂的运动规律与运动轨迹。

二、平面连杆机构设计的主要内容是根据给定的运动条件确定机构运动简图的尺寸参数。

在实际生产中，设计平面连杆机构的实际问题是多种多样的，给定的条件也各不相同，归纳起来设计的问题一般可以分为两类基本问题。

1. 实现已知的运动规律当原动件的运动规律已知时，所确定的机构运动简图的尺寸参数应能保证从动件按照给定的运动规律而运动，这类设计问题也称为位置设计。

2. 实现已知的运动轨迹这类设计问题要使所确定的机构运动简图的尺寸参数应能保证该机构中作平面运动的构件上某一点沿着已知的运动轨迹运动，也称为轨迹设计。

三、平面四杆机构的运动设计平面四杆机构的运动设计是指根据给定的运动条件，确定机构中各个构件的尺寸。

有时还需要考虑机构的一些附加的几何条件或动力条件，如机构的结构要求、安装要求和最小传动角等，以保证机构设计得可靠、合理。

平面四杆机构的运动设计方法有解析法、图解法和实验法。

1 用图解法设计主要通过几何作图来设计四杆机构，首先根据设计要求找出机构运动的几何尺寸之间关系，然后按比例作图并确定出机构的运动尺寸，这种方法比较直观，由于作图过程会有一定的误差，因此精度不高。

连杆机构优化设计连杆机构是最常用的机构，因此连杆机构优化设计在机构设计中十分重要，研究工作开展得也最为广泛。

有大量的文献介绍有关平面四杆机构、平面五杆机构、柔性连杆机构、曲柄连杆机构、槽轮连杆机构、凸轮连杆组合机构和齿轮连杆等机构的优化。

鉴于四连杆机构的典型性，本节结合四连杆机构的函数再现优化设计问题，阐述连杆机构优化问题的一般方法及流程。

四连杆机构的优化设计就是对四连杆机构的参量进行优化调整，使得机构给定的运动和机构所实现的运动之间误差最小。

因此四连杆机构的优化设计的过程，就是寻找使得四连杆机构运动误差最小的一组机构设计参量。

四连杆机构设计参量确定后，就可认为实现了机构的优化设计。

四连杆机构的优化设计包括四连杆机构优化模型建立和优化模型求解二个主要过程。

通过对四连杆机构的分析确定优化方案，确定设计变量，给出目标函数，并将机构设计制约条件，如杆长条件、传动角条件等，写成相应的约束条件，即可建立机构优化设计模型。

下面介绍四连杆机构函数再现优化设计模型的建立。

连杆机构函数再现设计主要通过选取输人构件和输出构件相对应若干位置、采用机构图解法或分析法确定机构各参数。

图1是典型的平面铰链四杆机构，、、和分别表示于四个构件的长度，杆AB是输入构件。

假设图1所示的平面铰链四杆机构再现给定函数为，即，则机构位置取决于、、、铰链A的位置、AD与机架x轴夹角以及输人构件转角等七个变量。

图1 平面铰链四杆机构为简化问题，可令A的位置为，，构件的长度为1(参考构件)，由此可将问题维数降为四维，并不影响构件输入、输出的函数关系。

由此可以得到输出构件转角外与输入构件转角之间的函数关系式：（1）机构优化设计目标就是使得输出构件转角与给定值在，所有位置上的误差最小。

因此机构优化设计的目标函数可用下式表示（2）当输入构件转角为时，输出构件转角外可由下式求得，（3）式中：所以（4）将上式代入式（3），并令代表设计变量、、及，机构优化设计目标函数可写为：（5）机构优化设计的约束条件应根据机构设计的实际情况确定。