1.2 全排列及其逆序数

1.2.1 排列与逆序定义1.2.1由自然数1，2，······，n 组成的一个有序数组称为一个n 元排列.例如：1，2，3，4，55，1，2，3，45，3，2，1，4都是数1，2，3，4，5的一个排列.问题：n 个数的不同排列有个.n !标准排列(自然排列).按数的大小次序，由小到大的排列称为定义n 阶排列1234…n 称为n 阶自然序排列.计算排列的逆序数的方法：分别计算出排在1,2,…,n-1,n前面比它大的数码之和即分别算出1,2,…,n-1,n这n个元素的逆序数，这个元素的逆序数的总和即为所求排列的逆序数例1 求排列32514的逆序数.解在排列32514中,3排在首位,逆序数为0;2的前面比2大的数只有一个3,故逆序数为1;3 2 5 1 401031于是排列32514的逆序数为(32514)01031τ=++++.5=5的前面没有比5大的数,其逆序数为0;1的前面比1大的数有3个,故逆序数为3;4的前面比4大的数有1个,故逆序数为1;例2 计算下列排列的逆序数()2179863541解453689712544310010(217986354)τ=18=54+0100134+++++++()()()212321n n n−−L 解()()(12321)n n n τ−−L ()()12321n n n−−L 0=000000考虑，在1，2，3 的全排列中有个偶排列：有个奇排列：123，231，312 132，213，32133一般说来，在n个数码的全排列中，奇偶排列各占一半.定义1.2.4把一个排列中的任意两个数交换位置，而其余数码不动，叫做对该排列作一次对换，简称对换.将相邻的两个数对换，称为相邻对换.ml b b a a L L 11例如b a ml b b a a a L L 11a b nm l c c b b a a L L L 111n m l c c a b b b a a L L L 111b a a 2.对换定理1 一个排列中的任意两个元素对换，排列改变奇偶性．证明设排列为m l b b ab a a L L 11对换与a bml b b ba a a L L 11除外，其它元素的逆序数不改变.b ,a ba a b 的逆序数不变;经对换后的逆序数增加1 ,当时，b a <当时，b a >经对换后的逆序数不变，的逆序数减少1.a b 因此对换相邻两个元素，排列改变奇偶性.设排列为nm l c bc b ab a a L L L 111现来对换与a .b 次相邻对换m nm l c c b b ab a a L L L 111次相邻对换1+m n m l c c a b b b a a L L L 111,111n m l c bc b ab a a L L L ∴次相邻对换12+m ,111nm l c ac b bb a a L L L 所以一个排列中的任意两个元素对换，排列改变奇偶性.nm l c c b b b a a a L L L 111ab2!n q p ==定理任意一个n 阶排列都可以经过一系列对换变成自然序排列，并且所作对换的次数与该排列有相同的奇偶性.证明用数学归纳证明当n=1时，结论显然成立.假设结论对n-1阶排列成立,现证对n 阶排列也成立..,,,21阶排列是任一设n j j j n L ,n j n =若.1,,,121阶排列个是一则−−n j j j n L 由假设知，121,,,−n j j j L 可经过一系列对换变成自然序排列，从而nn j j j j ,,,,121−L 可经过一系列对换变成自然序排列.),,,n n j n n j 则先作对换（若≠n n n n j j j j j j j j ′′′′−−,,,,,,,,121121L L 变成使这就归结为上面的情形，结论成立.所以任意一个n 阶排列都可以经过一系列对换变成自然序排列.由于自然序排列是偶排列，由定理1可知，对换一个改变排列奇偶性，所以将一奇排列变成自然序排列推论需要作奇数次对换，而将一偶排列变成自然序排列则需要作偶数次对换,证毕.任意两个n 阶排列都可以经过一系列对换互变，而且若这两个排列的奇偶性相同，则所作的则所作的对换次数是奇数.对换次数是偶数；若这两个排列的奇偶性相反，小结1.排列,逆序数，奇排列,偶排列,对换的定义.2.一个排列中的任意两个元素对换，排列改变奇偶性．思考题证明在全部阶排列中,奇偶排列各占一半. n ()2≥n 思考题解答证设在全部阶排列中有个奇排列, 个偶排列,现来证.n s t t s =将个奇排列的前两个数对换,则这个奇排列全变成偶排列,并且它们彼此不同,所以s s .t s ≤若将个偶排列的前两个数对换,则这个偶排列全变成奇排列,并且它们彼此不同,于是有t t .s t ≤故必有.t s =作业：P251（1）（5）2（1）（2）3（2）4（1）56 （1）（3）。

全排列及其逆序数
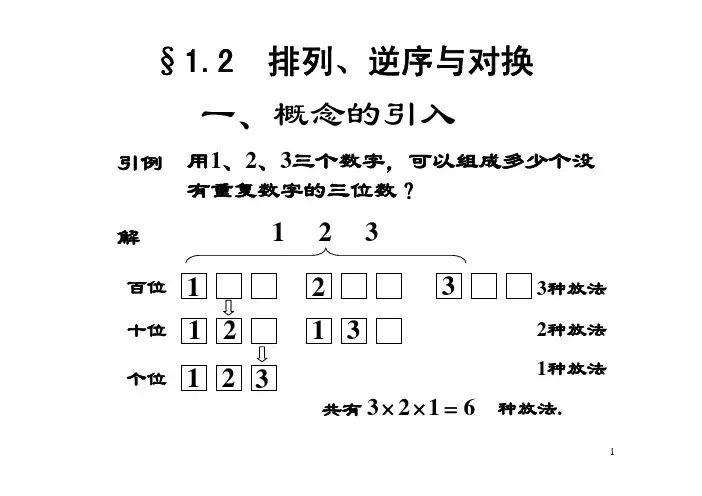
一、概念的引入引例用1、2、3三个数字，可以组成多少个没有重复数字的三位数？解1 2 3123百位3种放法十位1231个位1 232种放法1种放法种放法.共有二、全排列及其逆序数问题定义由引例同理例如排列32514 中，定义我们规
定各元素之间有一个标准次序, n 个不同的自然数，规定由小到大为标准次序.排列的逆序数3 2 5 1 4定义
一个排列中所有逆序的总数称为此排列的逆序数.例如排列32514 中， 3 2 5 1 4逆序数为31故
此排列的逆序数为3+1+0+1+0=5.计算排列逆序数的方法方法1逆序数为奇数的排列称为奇排列;逆序数为偶数的排列称为偶排列.排列的奇偶性分别计算出排列中每个元素前面比它大的数码个数之和，即算出排列中每个元素的逆序数，这每个元素的逆序数之总和即为所求排列的逆序
数.方法2例1 求排列32514的逆序数.解在排列32514中,3排在首位,逆序数为0;2的前面比2大的数只有一个3,故逆
序数为1;3 2 5 1 4于是排列32514的逆序数为5的前面没有比5大的数,其逆序数为0;1的前面比1大的数有3个,故
逆序数为3;4的前面比4大的数有1个,故逆序数为1;例2 计算下列排列的逆序数，并讨论它们的奇偶性.解此排列为偶排列.解解
2 排列具有奇偶性.
3 计算排列逆序数常用的方法有2 种.三、小结思考题分别用两种方法求排列16352487的逆序数.思考
题解答解用方法11 6 3 5 2 4 8 7 用方法2由前向后求每个数的逆序数.。