下载文档原格式
一、概述霍夫变换是一种常用的图像处理技术，它可以用于检测图像中的直线、圆或者其他形状。
它具有很好的鲁棒性，可以应对图像中存在的噪声和其他干扰。
霍夫变换在计算机视觉、图像处理和模式识别领域有着广泛的应用，成为了处理图像中几何形状的重要工具。
二、霍夫变换的原理霍夫变换最初是由美国科学家保罗·霍夫在1962年提出的，用于检测图像中的直线。
后来，霍夫变换被扩展到检测圆或者其他形状。
霍夫变换的基本原理是将空间域中的坐标转换到参数域中，在参数域中对应的曲线经过的点在空间域中具有共线的特点。
通过累加空间域中的点的参数，可以找到曲线或者形状的参数方程，从而实现对图像中形状的检测。
具体来说，对于检测直线来说，可以通过霍夫变换将直线表示为参数空间中的斜率和截距，从而可以在参数空间中进行累加，最终找到直线的参数方程。
三、霍夫变换在直线检测中的应用1. 边缘检测在使用霍夫变换检测直线之前，通常需要对图像进行边缘检测。
边缘检测可以帮助找到图像中明显的过渡区域，这些过渡区域通常对应着直线的轮廓。
常用的边缘检测算法包括Sobel算子、Canny算子等。
2. 参数空间的设置为了使用霍夫变换来检测直线，需要设定参数空间的范围。
对于直线检测来说，一般可以设定直线的斜率和截距的取值范围。
3. 累加过程在设定好参数空间后，需要对图像中的边缘点进行霍夫变换的累加过程。
对于每一个边缘点，都可以在参数空间中找到对应的直线，通过对参数空间的累加，可以找到参数空间中的峰值，这些峰值对应着图像中的直线。
4. 直线检测可以根据参数空间中的峰值来确定图像中的直线。
通常可以设定一个阈值来筛选参数空间中的峰值，从而得到最终的直线检测结果。
四、霍夫变换在圆检测中的应用除了直线检测，霍夫变换也可以用于检测图像中的圆。
与直线检测类似，圆检测也需要进行边缘检测和参数空间的设定。
不同的是，在圆检测中，需要设定圆心和半径的参数空间范围。
五、霍夫变换的改进和应用1. 累加数组的优化在传统的霍夫变换中，需要对参数空间进行离散化，这会导致计算量较大。
matlabcanny边缘检测代码接霍夫变换-概述说明以及解释1.引言1.1 概述边缘检测是图像处理中的一个重要任务，它广泛应用于计算机视觉、图像分析和模式识别等领域。
边缘检测的目标是找到图像中不同区域之间的边界，并将其表示为像素强度的变化。
Canny边缘检测算法是一种经典且常用的边缘检测方法。
它通过一系列的图像处理步骤来提取图像中的边缘信息。
Canny算法的特点是能够检测出细且准确的边缘，并且对于图像中的噪声具有较好的抵抗能力。
Matlab是一种功能强大的数学软件，广泛应用于科学计算、数据可视化和图像处理等领域。
Matlab提供了丰富的图像处理函数和工具箱，其中包括了Canny边缘检测的实现代码。
本文的主要目的是介绍Matlab中Canny边缘检测的代码实现，并结合Hough变换算法进行边缘检测的应用。
通过使用Matlab中的相关函数和工具，我们可以有效地实现Canny边缘检测，并结合Hough变换来进一步处理和分析图像中的边缘特征。
本文将首先回顾Canny边缘检测算法的原理和步骤，然后介绍Matlab中的Canny边缘检测代码的使用方法。
接着，我们将介绍Hough 变换算法的原理和应用，并展示如何将Canny边缘检测与Hough变换相结合来实现更精确的边缘检测。
最后，我们将对Canny边缘检测和Hough变换的优缺点进行讨论，总结这两种方法在边缘检测中的应用。
同时，我们也将展望未来的研究方向，探讨如何进一步改进和优化边缘检测算法，以满足不断发展的图像处理需求。
通过阅读本文，读者将能够理解Canny边缘检测算法和Hough变换算法的原理，掌握Matlab中相关代码的使用方法，并了解边缘检测在实际应用中的优势和局限性。
希望本文能为读者在图像处理领域的学习和研究提供一定的帮助和启示。
文章结构是指文章的整体框架和组织形式。
一个良好的文章结构可以使读者更好地理解和领会文章的内容，同时也有助于文章的逻辑性和条理性。
基于matlab的直线检测原理
基于Matlab的直线检测原理涉及到一种称为霍夫变换的方法。
霍夫变换是一种在图像处理中常用的方法，用于检测图像中的直线。
下面是基于Matlab的直线检测原理的具体步骤：
1. 读取图像：首先，在Matlab中读取需要进行直线检测的图像。
2. 边缘检测：使用Matlab提供的边缘检测算法（例如Canny
算法）来检测图像中的边缘。
这可以通过调用Matlab中的imedge函数来实现。
3. 霍夫变换：使用Matlab中的hough函数来执行霍夫变换。
霍夫变换将边缘图像转换为霍夫空间，其中每个点对应于直线在原始图像中的参数。
通过设置适当的阈值和其他参数，可以控制检测到的直线的数量和质量。
4. 直线提取：通过分析霍夫变换的结果，在霍夫空间中找到具有最高数量的交点，这些交点对应于图像中的直线。
可以使用Matlab的houghpeaks函数来找到霍夫空间中的交点。
5. 直线可视化：使用Matlab中的houghlines函数来提取直线
的位置和角度，并在原始图像上绘制检测到的直线。
这将帮助用户看到直线检测的结果。
需要注意的是，直线检测的结果可能会受到图像质量、边缘检
测算法的选择和参数设置的影响。
因此，在实际应用中，可能需要不断调整参数以获得更好的直线检测结果。
matlabcanny边缘检测代码接霍夫变换全文共四篇示例，供读者参考第一篇示例：Matlab是一个强大的数学软件工具，其图像处理工具箱可以帮助我们进行各种图像处理操作，比如边缘检测和霍夫变换。
本文将分享如何使用Matlab进行Canny边缘检测，并结合霍夫变换进行线检测。
Canny边缘检测是一种经典的边缘检测算法，它的优点是能够检测到边缘的细节，并且对噪声具有一定的鲁棒性。
在Matlab中，我们可以通过一行简单的代码来实现Canny边缘检测：```edgeImage = edge(rgb2gray(image), 'canny');```以上代码中，我们首先将原始图像转换为灰度图像，然后调用Matlab的'edge'函数，并指定边缘检测算法为Canny，最后我们将得到的边缘图像存储在edgeImage中。
接下来，我们可以将边缘图像显示出来，以便进行进一步的处理和分析。
```imshow(edgeImage);通过上述代码，我们可以看到Canny边缘检测算法的效果，边缘比较清晰，同时也保留了边缘的细节信息。
接下来，我们将介绍如何使用霍夫变换来进行线检测。
霍夫变换是一种经典的图像处理算法，其主要应用是检测直线和圆等几何形状。
在Matlab中，我们可以通过一行代码来实现霍夫变换的线检测：```[H,theta,rho] = hough(edgeImage);peaks = houghpeaks(H, 10);lines = houghlines(edgeImage, theta, rho, peaks);imshow(image);hold on;for k = 1 : length(lines)xy = [lines(k).point1; lines(k).point2];plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');endhold off;以上代码中，我们首先调用Matlab的'hough'函数来计算霍夫变换的极坐标空间。
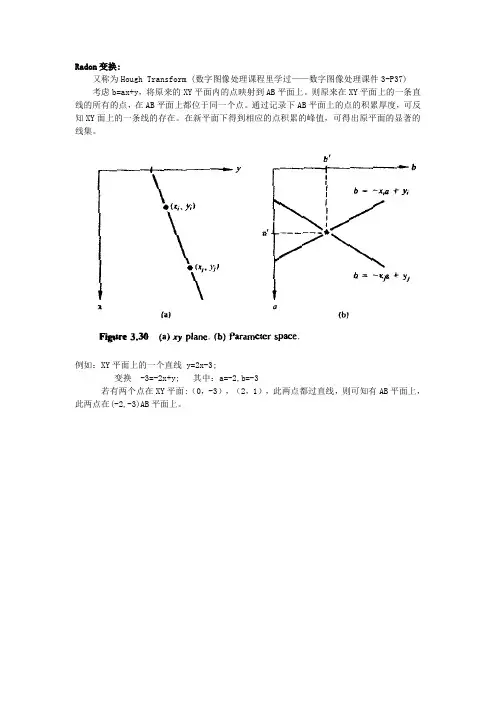
Radon变换:又称为Hough Transform(数字图像处理课程里学过——数字图像处理课件3-P37)考虑b=ax+y，将原来的XY平面内的点映射到AB平面上。
则原来在XY平面上的一条直线的所有的点，在AB平面上都位于同一个点。
通过记录下AB平面上的点的积累厚度，可反知XY面上的一条线的存在。
在新平面下得到相应的点积累的峰值，可得出原平面的显著的线集。
例如：XY平面上的一个直线y=2x-3;变换-3=-2x+y;其中：a=-2,b=-3若有两个点在XY平面:（0，-3），（2，1），此两点都过直线，则可知有AB平面上，此两点在(-2,-3)AB平面上。
一种更好的表示方法是用ρ和θ来代替ab。
即：xcosθ+ysinθ=ρ以图像的中心为极坐标原点，直线X`即为新的投影坐标，θ为角度。
我们所要求的原坐标上的一条直线，是一条垂直于上图X`的一条直线，而非X`本身。
如下例：function radontestI=zeros(200,200);%I(100:170,100:170)=1;A=eye(100,100);I(101:200,1:100)=A;figure,imshow(I);title('orginal image');orginal imagetheta=0:180;[R,xp]=radon(I,theta);%R是点的数量多少%xp是R对应的坐标位置,即为X`，另一解释为直线跟原点间距离%0-180代表0到180度%此变换是以图像的中心点为原点的变换figure,imagesc(theta,xp,R);title('R_theta X');xlabel('theta(degree)');ylabel('X\prime');colormap(hot);colorbar;即所求 =45度，X`=-75左右。
意思是在原XY坐标下的45度的直线X`上，距离原点75的位置有条与X`垂直的直线。
一、引言霍夫变换是一种常用的图像处理技术，它可以用来检测图像中的直线、圆或者其他形状。
在图像处理领域，霍夫变换被广泛应用于计算机视觉、模式识别、目标检测等多个领域。
在本文中，我们将重点介绍如何利用霍夫变换来检测多边形，并使用Matlab编程实现该过程。
二、霍夫变换原理霍夫变换是一种基于数学原理的图像处理技术，它的基本原理是将图像中的特定形状表示为参数空间中的曲线或者点，在参数空间中进行投票统计，从而找到图像中的对应形状。
对于直线检测来说，霍夫变换将直线表示为参数空间中的斜率和截距，然后通过投票统计找到图像中的直线。
三、多边形检测方法在图像处理中，多边形通常可以用一组直线段来表示，因此我们可以利用霍夫变换来检测图像中的直线段，然后根据直线段的位置和方向来拟合出多边形。
具体来说，多边形检测的方法包括以下几个步骤：1. 边缘检测：首先需要对图像进行边缘检测，将图像中的边缘提取出来，这可以通过Canny边缘检测算法来实现。
2. 霍夫变换：对于得到的边缘图像，我们可以利用霍夫变换来检测其中的直线段，这可以通过Matlab中的hough函数来实现。
3. 直线拟合：根据霍夫变换得到的直线段，我们可以利用最小二乘法或者其他拟合算法来将这些直线段拟合成多边形。
四、Matlab实现以下是利用Matlab实现多边形检测的示例代码：```matlab读取图像img = imread('polygon.png');边缘检测edge_img = edge(img, 'Canny');霍夫变换[H, theta, rho] = hough(edge_img);寻找直线段P = houghpeaks(H, 10);lines = houghlines(edge_img, theta, rho, P);显示结果figure, imshow(img), hold onfor k = 1:length(lines)xy = [lines(k).point1; lines(k).point2];plot(xy(:,1), xy(:,2), 'LineWidth', 2, 'Color', 'green');end```通过以上代码，我们可以实现图像中多边形的检测，并在图像上显示出检测到的直线段，从而得到多边形的拟合结果。
霍夫变换霍夫检测-直线 前提条件 – 边缘检测已经完成，霍夫变换解决平⾯空间到极坐标空间转换。
从霍夫空间曲线图来看，取不同的像素点都汇聚在⼀个点，这表明这些个像素点都属于同⼀条直线。
（x i,y i）.对于任意⼀条直线上的所有点来说变换到极坐标中，从[0~360]空间，可以得到r的⼤⼩属于同⼀条直线上点在极坐标空(r, θ)必然在⼀个点上有最强的信号出现（如上图），根据此反算到平⾯坐标中就可以得到直线上各点的像素坐标。
从⽽得到直线。
下图第⼀张为原图，第⼆张为提取边缘，第三张为直线检测并绘制。
霍夫检测-圆 极坐标变换原理： 从平⾯坐标到极坐标转换三个参数C（x0,y0,r）其中(x0,y0)是圆⼼假设平⾯坐标的任意⼀个圆上的点，转换到极坐标中：C（x0,y0,r）处有最⼤值，霍夫变换正是利⽤这个原理实现圆的检测。
霍夫圆检测对噪声⽐较敏感，所以⾸先要对图像做中值滤波。
相关函数如下:1//标准的霍夫变换HoughLines从平⾯坐标转换到霍夫空间，2//最终输出是表⽰极坐标空间霍夫变换直线概率,要⾃⼰反变换到平⾯空间，⼀般不⽤;3 HoughLinesP（int1，out1,）最终输出是直线的两个点（x1,y1，x2,y2）.45霍夫直线检测HoughLinesP(out1,plinel,1,CV_PI/180.0,10,0,0);6// out1为要检测的灰度图像，plinel 为输出的直线的两点，类型为vector<Vec4f>plinel;7// 1为⽣成极坐标时候的像素扫描步长，CV_PI/180.0⽣成极坐标时候的⾓度步长，⼀般取值CV_PI/180，10为阈值，8//只有获得⾜够交点的极坐标点才被看成是直线，最⼩直线长度0最⼤间隔0；9for (size_t i=0;i<plinel.size();i++)10 {11 Vec4f hline = plinel[i];12 line(out2, Point(hline[0], hline[1]),13 Point(hline[2], hline[3]),14 colorf3, 3, 8);15 }1617霍夫圆检测HoughCircles(out2, pcircle, CV_HOUGH_GRADIENT,1, 10, 100, 30,80,100);18//out2为要检测的灰度图像，pcircle 为输出的圆⼼及半径，类型为vector<Vec3f>pcircle;19//10 最短距离-可以分辨是两个圆的，否则认为是同⼼圆，30为中⼼点累加器阈值⽤于确定圆⼼80为最⼩半径100最⼤半径，20 Mat dst = Mat(in1_image.size(), in1_image.type());21for (size_t i=0;i< pcircle.size();i++)22 {23 Vec3f cc = pcircle[i];24 circle(dst,Point(cc[0], cc[0]), cc[2], colorf3,2,LINE_AA);25 circle(dst, Point(cc[0], cc[0]), 3, colorf, 2, LINE_AA);26 }。
