残差分析(课堂PPT)

第四节残差分析、预报和控制一、残差分析前面咱们介绍了线性回归方程的成立和查验。

在实际问题中，由于观察人员的粗心或偶然因素的干扰。

常会使咱们所取得的数据不完全靠得住, 即出现异样数据。

有时即便通过相关系数或F查验证明回归方程靠得住，也不能排除数据存在上述问题。

残差分析的目的就在于解决这一问题。

所谓残差是指实际观察值与回归估量值的差，即(2-1-26)显然，有多少对数据，就有多少个残差。

残差分析就是通过残差所提供的信息，分析出数据的靠得住性、周期性或其它干扰。

第一介绍如何检查异样数据。

异样数据是指与其它数据产生的条件有明显不同的数据，因此异样数据的残差会特别的大。

一旦发觉异样数据应及时剔除，用剩余数据从头成立回归方程，以提高回归方程的质量。

发觉异样数据主要从技术上找原因，当技术上无法找到原因时，就得借助于数理统计方式。

由数理统计方式能够证明(2-1-27) 或记为(2-1-28)这说明残差的方差D(e)是x的函数，且二者呈曲线关系。

以回归方程及方程和作图。

见方开泰《实用回归分析》P45图考虑到较小，当n较大时(2-1-29) 现在图中的两条曲线可近似于两条平行直线。

从而有(2-1-30) 或近似地(2-1-31)这表明，当n较大时y i落在图2-1-3的长条形带子中的概率约为95%，只要明白，就可以够取得残差的置信区域。

一般是未知的，通常常利用残差标准差来估量。

可用下式求得(2-1-32) 由此可得残差置信带(2-1-33)对残差在置信带之外的数据都要进行检查，以区别是不是是异样数据，若是是异样数据就要剔除掉。

此刻咱们对例1做残差检查。

由式(2-1-32)残差置信带为,。

计算5个实验点的预报值与残差值(见表2-1-4)，并作出残差检查图(见图2-1-4)表2-1-4 例1的残差值图2-1-4 例1的残差图由图2-1-4可见，例1中全数数据的残差都在置信带内，没有异样数据。

除此之外，残差图还能够为咱们提供许多有效信息。

残差分析初步——残差图
2009年09月18日星期五 11:30
所有残差应在0左右随机波动，并且变化幅度在一条带内。

但由该图，我们却可以清楚地看到随着年龄的增长，残差变化幅度降低。

由此判定存在异方差现象，需要使用非线性的方法拟合。

2
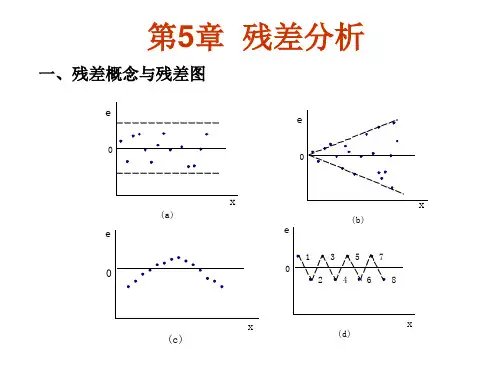
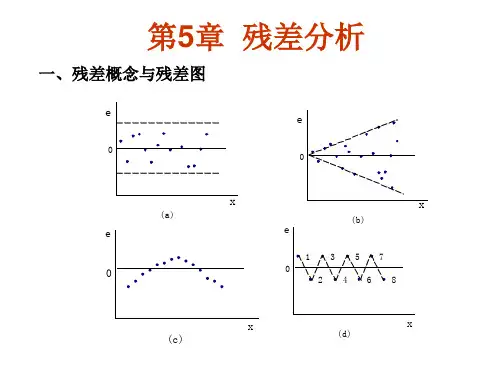
a 线性关系成立。

b x加入二次方项
c 存在异方差，需要改变x形式
d 残差与时间t有关。

可能遗漏变量或者存在序列相关，需要引入变量。

3 是否需要引入时间t
下图e是残差，x是时间，即月份1到12。

4 、Standardized predicted values (*ZPRED), Standardized residuals (*ZRESID),
Source variable list. Lists the dependent variable (DEPENDNT) and the following predicted and residual variables: Standardized predicted values (*ZPRED), Standardized residuals (*ZRESID), Deleted residuals (*DRESID), Adjusted predicted values (*ADJPRED), Studentized residuals (*SRESID), Studentized deleted residuals (*SDRESID).
5、Durbin-Watson Test ：检测回归分析中的残差项是否存在自相关。

§2.3 残差分析前面主要假设: 线性, 误差独立同正态分布. 问题1: 如何考察这些特点;问题2: 若不满足, 如何调整使其符合或近似符合. 方法: 从残差出发,分析误差项假定的合理性等特点1. 误差项的正态性检验第一章中介绍的正态性检验方法可用残差的检验.(1) 学生化残差(残差除于它的标准差的估计值) 若2~(,)N ε0I , 则残差向量()2ˆ~0,()N σ-εI H , 其中()1T T -=X X X X H , 由此可知 2ˆ~(0,(1)),1~i ii N h i n εσ-= 这里1()T T ii i i h -=x X X x (杠杆量)1,1(1,,,)T i i i p x x -=x易知2ˆV a r ()(1)i i i h εσ=-, 一般不等, 用2ˆMSE σ=代2σ, 标准化得ˆ,1~(1)i i ii r i n MSE h ε==⋅-当n 较大时, i r 近似地相互独立且服从~(0,1)N .(2) 残差正态性的频率检验基本思想:在一些范围内, 学生化残差频率≈标准正态频率. 设~(0,1)N ξ, 则 ξ(1,1)- ( 1.5,1.5)- (2,2)- P0.68 0.870.95若学生化残差i r 也有类似的结果, 则认可为正态. 例5 对例3, 检验误差正态性假定的合理性.解 调用proc reg(example2_5)过程, 得表2.6(略) 与(0,1)N 的概率类似. 无理由拒绝误差项正态假设.(3) 残差的正态QQ 图1) 学生化残差的正态QQ 图的做法(i) 将1,,n r r 由小到大排序(1)(),,n r r ;(ii) 计算1()0.3750.25i i q n Φ--⎡⎤=⎢⎥+⎣⎦;(iii) 描出点()()(,),1~i i q r i n =;2) 直观检验法若散点基本上在一直线上, 则认可误差为正态.3) 相关系数检验法 若()()122()()11()()ˆ1()()ni i i n n i i i i r r q q rr q q ρ===--=≈-⋅-∑∑∑ 则认可为正态.例6 对表2.6中学生化残差,作QQ 图,并分析合理性.解调用example2_6得QQ图, 大致在一直线上, 可认误差项为正态.2. 残差图分析y X或某序号等.纵坐标: 残差ˆ ; 横坐标: ˆ,j直观地判断合理性、有无必要引入交叉项、遗漏项SAS中主调用proc plot和proc gplot过程.(1) 以因变量Y 的拟合值为横坐标的残差图若关系确为线性且2~(,)N σε0I , 则ˆ=YHY 与 ˆ()=-εI H Y 不相关.(且相互独立),则显示为图(a).线性关系, 误差正态 误差的等方差性不符回归函数非线性(应有二次项) 可能遗漏了有线性关系的量(2) 以自变量观测值为横坐标的残差图情形与上类似.(3) 时序残差图较满意的仍是图2.2中的(a), 其他类似的含义.例7 根据例3和例5, 考察模型假定条件的合理性.都较合理3. Box-Cox 变换残分后,若不足,需改进,使其符“线回,独立,等方差”. 大多0Y >(或使其>0), 作()1Y Y λλλ-=, 待定0λ≠对12,,,n y y y , 作上述变换, 得()()()()12(,,,)T n y y y λλλλ=Y ,使()λ=+Y X βε, 2~(,)N σε0I用最大似然法求出λ. 参见[16], 转化为使()()1()(;)()(())T T T SSE I λλλλ-=-Z Z X X X X Z 达到最小, 其中()()()()12(,,)T n z z z λλλλ=Z ,1()()1n n i i i i z y y λλλ-=⎡⎤=∏⎢⎥⎣⎦,通过取一系列的λ,计算()(;)SSE λλZ ,比大小定λ.(注: 当0λ=时, ()ln YY λ=即可).例8 54位肝病人术前数据与术后生存时间如下表.(1) 若用线性回归模型拟合, 考察其各假设合理性;(2) 用Box-Cox变换,确定 ,再用“线回”的合理性? 解: 调用example2_8过程, 得(1) 由两图知, 直接拟合为0112244Y X X X ββββε=++++不很恰当(且ˆ0.8191ρ=相差较大). (2) 对Y 作Box-Cox 变换, 从()(;)SSE λλZ图知,取0.07λ=, 故作0.0710.07Y Z -= (表2.7最后一列)对Z 用线回拟合较好.拟合的0112244Z X X X ββββε=++++方差分析及参数估计结果如表2.8所示.实用中λ灵活选取. 还有其他诊断方法.。