方差分析单因素模板

什么是单因素方差分析单因素方差分析是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。

单因素方差分析是两个样本平均数比较的引伸，它是用来检验多个平均数之间的差异，从而确定因素对试验结果有无显著性影响的一种统计方法。

单因素方差分析相关概念•因素：影响研究对象的某一指标、变量。

•水平：因素变化的各种状态或因素变化所分的等级或组别。

•单因素试验：考虑的因素只有一个的试验叫单因素试验。

单因素方差分析示例[1]例如，将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象，以致减少了药效。

下表列出了5种常用的抗生素注入到牛的体内时，抗生素与血浆蛋白质结合的百分比。

现需要在显著性水平a = 0.0!下检验这些百分比的均值有无显著的差异。

设各总体服从正态在这里，试验的指标是抗生素与血浆蛋白质结合的百分比，抗生素为因素，不同的5种抗生素就是这个因素的五个不同的水平。

假定除抗生素这一因素外，其余的一切条件都相同。

这就是单因素试验。

试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异。

即考察抗生素这一因素对这些百分比有无显著影响。

这就是一个典型的单因素试验的方差分析问题单因素方差分析的基本理论⑴备择假设Hi,然后寻找适当的检验统计量进行假设检验。

本节将借用上面的实例来讨论单因素试验的方差分析问题。

2厂…j $）下进行了nj = 4次独立试验，得到如上表所示的结果。

这些结果是一个随机变量。

表中的数据可以看成来自s个不同总体（每个水平对应一个总体）的样本值，将各个总体的均值依次记为山、》2、…r »则按题意需检验假设页：旳=“2 =…=川尸1 : \J “5不全相等为了便于讨论，现在引入总平均卩[Ho :屍="2 =…=毎=qI 闻:力屆…：吗不全为零因此，单因素方差分析的任务就是检验s个总体的均值®是否相等，也就等价于检验各水平Aj的效应6是否都等于零。

样本产恥…佔吁/来自正态总体N （虬2）, 9与02未知，且设不同水平Aj 下的样本 之间相互独立，则单因素方差分析所需的检验统计量可以从总平方和的分解导出来。

1g2g282.3979319.0735316.65363g313.7519307.702312.87093g+2g+1g342.2044286.8267306.90311g+1g+1g326.451281.5521296.17771g+2g261.4286315.1616290.57412g+1g272.5417298.304296.65931g+2g+3g324.7711276.5006279.6137ck274.7973313.2938287.51982683.5962721.9522684.73600000720169074090227207807000009992424174总差异10318.6水平差异1980.736(处理间)竖直差异105.8326105.8326误差8232.058337.884总自由度268216n(区组)=k（处理）=水平间自由度方差分析表误差e188337.884463.2158总变异2610318.62F检验0.534507无显著差异12.42599处理1g0002g0003g003g+2g+1g01g+1g+1g1g+2g2g+1g1g+2g+3gck 秩次距a，fe=18SSR0.05SSR0.01Sy LSR0.05LSR0.012 2.97 4.0712.4259936.9051950.573783 3.12 4.2512.4259938.7690952.810464 3.21 4.3612.4259939.8874354.177325 3.27 4.4512.4259940.6329955.295666 3.32 4.5112.4259941.2542956.041227 3.36 4.5612.4259941.7513356.662528 3.38 4.612.4259941.9998557.15956假设H 01：处理间无显著差异假设H 02：区组间无显著差异SSR 多重比较：FA大于F临界值，Ho不成立。

单因素方差分析完整实例.doc单因素方差分析是统计学中常用的分析方法之一，用于比较结果在一个分类变量（即因素）的不同组别之间的差异。

下面将通过一个实例来介绍单因素方差分析的具体应用。

实例介绍：某公司招聘了25名新员工，并在这些员工入职一个月后进行了一次工作满意度调查。

调查结果显示，他们对公司的工作满意度总体得分为80分，但是有些员工对公司的工作并不满意。

公司希望了解员工的不满意来源，并查看不同部门、教育程度和薪水水平对工作满意度是否有影响。

公司收集了员工的部门、教育程度和薪水水平等信息，并对这些因素对工作满意度的影响进行了单因素方差分析。

实例步骤：1.数据整理首先，将员工的部门、教育程度和薪水水平等信息整理成表格形式。

随机抽取10名员工的数据如下：| 员工编号 | 部门 | 教育程度 | 薪水水平 | 工作满意度得分 || :------: | :--: | :------: | :------: | :------------: || 1 | A | 大学 | 高薪 | 85 || 2 | B | 高中 | 中薪 | 83 || 3 | C | 硕士 | 中薪 | 78 || 4 | A | 高中 | 低薪 | 77 || 5 | B | 大学 | 高薪 | 93 || 6 | C | 大学 | 中薪 | 80 || 7 | A | 高中 | 中薪 | 72 || 8 | B | 大学 | 中薪 | 85 || 9 | C | 硕士 | 高薪 | 89 || 10 | A | 高中 | 高薪 | 75 |2.数据分析进行单因素方差分析时需要分别计算各组数据的均值和方差。

2.1 计算各组均值首先，按照不同部门计算均值：| 部门 | 员工数 | 工作满意度均值 || :--: | :----: | :------------: || A | 4 | 77.25 || B | 3 | 87.00 || C | 3 | 82.33 || 总计 | 10 | 82.00 |由上述计算结果可得出不同因素组别的均值。

什么是单因素方差分析单因素方差分析是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。

单因素方差分析是两个样本平均数比较的引伸，它是用来检验多个平均数之间的差异，从而确定因素对试验结果有无显著性影响的一种统计方法。

单因素方差分析相关概念●因素：影响研究对象的某一指标、变量。

●水平：因素变化的各种状态或因素变化所分的等级或组别。

●单因素试验：考虑的因素只有一个的试验叫单因素试验。

单因素方差分析示例[1]例如，将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象，以致减少了药效。

下表列出了5种常用的抗生素注入到牛的体内时，抗生素与血浆蛋白质结合的百分比。

现需要在显著性水平α = 0.05下检验这些百分比的均值有无显著的差异。

设各总体服从正态分布，且方差相同。

在这里，试验的指标是抗生素与血浆蛋白质结合的百分比，抗生素为因素，不同的5种抗生素就是这个因素的五个不同的水平。

假定除抗生素这一因素外，其余的一切条件都相同。

这就是单因素试验。

试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异。

即考察抗生素这一因素对这些百分比有无显著影响。

这就是一个典型的单因素试验的方差分析问题。

单因素方差分析的基本理论[1]与通常的统计推断问题一样，方差分析的任务也是先根据实际情况提出原假设H0与备择假设H1，然后寻找适当的检验统计量进行假设检验。

本节将借用上面的实例来讨论单因素试验的方差分析问题。

在上例中，因素A（即抗生素）有s（=5）个水平，在每一个水平下进行了n j = 4次独立试验，得到如上表所示的结果。

这些结果是一个随机变量。

表中的数据可以看成来自s个不同总体（每个水平对应一个总体）的样本值，将各个总体的均值依次记为,则按题意需检验假设不全相等为了便于讨论，现在引入总平均μ其中：再引入水平A j的效应δj显然有，δj表示水平A j下的总体平均值与总平均的差异。

利用这些记号，本例的假设就等价于假设不全为零因此，单因素方差分析的任务就是检验s个总体的均值μj是否相等，也就等价于检验各水平A j的效应δj是否都等于零。

单因素方差分析调查报告问题提出：对学院三个年级进行抽样，调查不同年级的同学的恋爱次数，样本均是独立的，试根据这些数据分析年级的不同对恋爱次数是否有影响？一、样本数据及P-P图由P-P图我们可以看出样本近似认为服从正态分布的。

二、提出假设原假设：H0:μ1=μ2=μ3 ，即年级对恋爱次数影响不显著；备择假设：H0:μ1,μ2，μ3不全等，即年级对恋爱次数有显著影响。

三、SPSS输出结果分析1、单因素方差分析描述恋爱次数上表说明，不同年级的同学的恋爱次数的方差齐性检验值为1.419，概率p值为0.244，p>0.05,无法拒绝原假设，说明各组的方差在a=0.05水平上没有显著性差异，即方差具有齐次性。

由此表可得即单因素方差分析表中F值为3.982，对应的P值为0.020 <0.05，所以应拒绝原假设，可以认为不同的年级对恋爱次数有显著性影响。

该结果虽然说明了三个年级对恋爱次数影响是显著性的，但是不能给出各年级两两之间的差异情况，要进一步了解各年级之间恋爱次数的差异情况，就需要进行多重比较：2、进行多重比较提出假设：H0:μi=μj H0:μi μj观察表中数据显著性可得结论：(1)：显著性0.624>0.05，所以接受原假设，即大一与大二的同学恋爱次数没有显著性差异；(2)：显著性0.031<0.05，所以拒绝原假设，即大一与大三的同学恋爱次数有显著性差异；(3)：显著性0.008<0.05，所以拒绝原假设，即大二与大三的同学恋爱次数有显著性差异。

四、统计决策由结论更进一步说明，大学生随着年级数的增加也是年龄的增加，恋爱次数也随之增加，希望同学们谨慎交友谨慎恋爱，在抓好学习的同时收获美满爱情。

一、
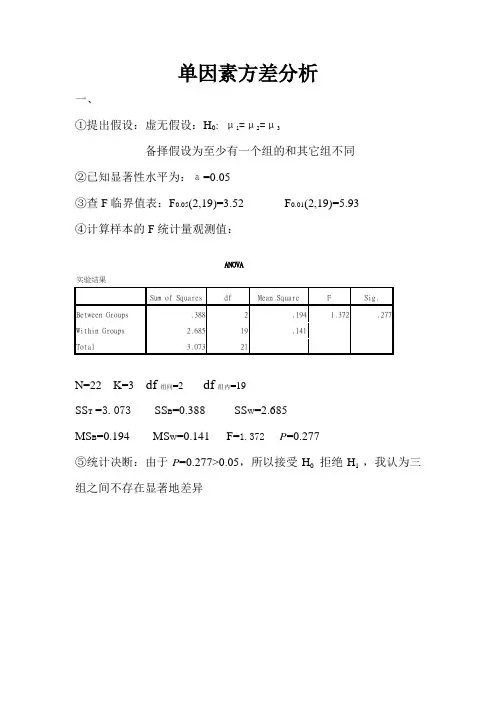
①提出假设：虚无假设：H0: μ1=μ2=μ3
备择假设为至少有一个组的和其它组不同
②已知显著性水平为：а=0.05
③查F临界值表：F0.05(2,19)=3.52 F0.01(2,19)=5.93
④计算样本的F统计量观测值：
N=22 K=3 df组间=2 df组内=19
SS T =3.073 SS B=0.388 SS W=2.685
MS B=0.194 MS W=0.141 F=1.372 P=0.277
⑤统计决断：由于P=0.277>0.05，所以接受H0拒绝H1 ，我认为三组之间不存在显著地差异
二、
①提出假设：虚无假设：H0: μ1=μ2=μ3
备择假设为至少有一个组的和其它组不同
②已知显著性水平为：а=0.05
③查F临界值表：F0.05(3,19)=3.13 F0.01(3,19)=5.01
④计算样本的F统计量观测值：
N=23 K=4 df组间=3 df组内=19
SS T =7636.870 SS B=2850.346 SS W=4786.524
MS B=950.115 MS W=251.922 F=3.771 P=0.028
⑤统计决断：由于P=0.028<0.05，所以拒绝H0接受H1 ，我认为三组之间存在显著地差异
⑤事后检验：
Post Hoc Tests
结论：通过事后检验表可以得到，治疗方案1与治疗方案4对患者的治疗效果是有显著的差异，治疗方案3与治疗方案4对患者的治疗效果是有极其显著的差异。

其余治疗方案之间或没有差异或差异不显著。

单因素方差分析范文单因素方差分析（One-way Analysis of Variance，简称ANOVA）是统计学中一种常用的方法，用于比较三个或三个以上的组的均值是否存在显著差异。

本篇文章将从原理、假设、步骤和应用等方面进行介绍。

一、原理二、假设在进行单因素方差分析时，需要假设组间均值是否存在显著差异。

具体的假设如下：H0：各组均值相等（即组间均值差异不显著）H1：至少有两组均值不相等（即组间均值差异显著）三、步骤进行单因素方差分析的步骤如下：1.根据研究目的和问题选择合适的统计方法；2.收集数据，涉及到多个组的测量值；3. 计算总平方和（SS_total），表示总变异性大小；4. 计算组间平方和（SS_between），表示组间变异性大小；5. 计算组内平方和（SS_within），表示组内变异性大小；6. 根据以上计算结果，计算组间均方（MS_between）和组内均方（MS_within）；7. 计算F值，即F=MS_between/MS_within；8.根据设定的显著性水平（通常为0.05），查表或计算得到临界值；9.比较计算得到的F值与临界值，判断是否达到显著性水平。

四、应用1.医学研究：比较不同药物对疾病治疗效果的影响；2.教育研究：比较不同教学方法对学生学习成绩的影响；3.市场调查：比较不同广告对产品销量的影响；4.农业实验：比较不同施肥方式对作物产量的影响。

五、总结单因素方差分析是一种常用的统计方法，通过比较三个或三个以上组的均值差异来判断各组之间是否存在显著差异。

它的优点是可以同时比较多个组均值的差异，从而提高实验效率和减少误判，应用广泛且实用。

因此，研究者在进行多组均值比较时，可以选择单因素方差分析方法进行分析。

单因素方差分析完整实例假设有一家医院的研究人员想要比较三种不同药物对高血压患者的降压效果。

为了进行实验，他们随机选择了60名患有高血压的病人，并将他们随机分成三组。

第一组患者接受药物A的治疗，第二组患者接受药物B的治疗，第三组患者接受药物C的治疗。

在治疗开始前，研究人员记录了每个患者的收缩压数据。

第一步是对数据进行描述性统计分析。

研究人员计算了每一组的平均值、标准差和样本量。

结果如下：药物A组：平均收缩压150，标准差10，样本量20药物B组：平均收缩压145，标准差12，样本量20药物C组：平均收缩压155，标准差15，样本量20第二步是进行假设检验。

研究人员的零假设是所有药物的降压效果相同，即三组的平均收缩压相等。

备择假设是至少有一组的平均收缩压不同。

为了进行单因素方差分析，我们需要计算组内方差和组间方差，然后进行F检验。

组内方差反映了每一组内部数据的离散程度，组间方差反映了不同组之间平均值的差异程度。

组内方差的计算方法是对每一组的方差进行平均，然后再对所有组的方差进行加权平均。

组间方差的计算方法是对所有组的平均值进行方差分析。

我们通过公式计算出组内方差为10.08，组间方差为58.67、接下来我们计算F值，F值是组间方差除以组内方差的比值。

F=组间方差/组内方差=58.67/10.08=5.81第三步是通过查找F分布表来计算p值。

根据自由度为2（组数-1）和df = 57（总样本量-组数）的F分布表，我们可以找到在F = 5.81条件下的p值。

假设我们选择显著性水平为0.05，我们发现在F分布表上，F=5.81对应的p值小于0.05、因此，我们拒绝零假设，接受备择假设。

这意味着至少有一组的平均收缩压与其他组有显著差异。

最后一步是进行事后检验。

由于我们有三组进行比较，我们可以使用事后检验方法来确定哪两组之间存在显著差异。

常用的事后检验方法包括Tukey HSD检验、Duncan检验等。

综上所述，单因素方差分析可以帮助我们判断不同组之间是否存在显著差异。

单因素方差分析案例雌性老鼠和雄性老鼠，在注射毒素后，经过一段时间，观察老鼠死亡和存活情况。

研究的问题是：老鼠在注射毒液后，死亡和存活情况，会不会跟性别有关？样本数据如下所示：（a代表雄性老鼠b代表雌性老鼠0代表死亡 1 代表活着tim 代表注射毒液后，经过多长时间，观察结果）点击“分析”——比较均值———单因素AVOVA, 如下所示：从上图可以看出，只有“两个变量”可选, 对于“组别（性别）”变量不可选，这里可能需要进行“转换”对数据重新进行编码，点击“转换”—“重新编码为不同变量”将a,b"分别用8,9进行替换，得到如下结果”此时的8 代表a(雄性老鼠）9代表b雌性老鼠，我们将“生存结局”变量移入“因变量列表”框内，将“性别”移入“因子”框内，点击“两两比较”按钮，如下所示：“勾选“将定方差齐性”下面的LSD 选项，和“未假定方差齐性”下面的Tamhane's T2选项点击继续点击“选项”按钮，如下所示：勾选“描述性”和“方差同质检验”以及均值图等选项，得到如下结果：结果分析：方差齐性检验结果，“显著性”为0，由于显著性0<0.05 所以，方差齐性不相等，在一般情况下，不能够进行方差分析但是对于SPSS来说，即使方差齐性不相等，还是可以进行方差分析的，由于此样本组少于三组，不能够进行多重样本对比从结果来看“单因素ANOVA”分析结果，显著性0.098，由于0.098>0.05 所以可以得出结论：生存结局受性别的影响不显著很多人，对这个结果可能存在疑虑，下面我们来进一步进行论证，由于“方差齐性不相等”下面我们来进行“非参数检验”检验结果如下所示：（此处采用的是“Kruskal-Wallis "检验方法）通过“Kruskal-Wallis ”检验方法，我们得出“sig=0.098" 跟我们先前分析的结果一样，都是0.098，事实得到论证。

单因素方差分析1.广告对销售额的影响ANOVA方差分析销售额销售额平方和df 均方 F 显著性组间（组合）5866.083 3 1955.361 13.483 .000 线性项对比2101.250 1 2101.250 14.489 .000 偏差3764.833 2 1882.417 12.980 .000 组内20303.222 140 145.023总数26169.306 143描述销售额N 均值标准差标准误均值的95% 置信区间极小值极大值下限上限报纸36 73.2222 9.73392 1.62232 69.9287 76.5157 54.00 94.00 广播36 70.8889 12.96760 2.16127 66.5013 75.2765 33.00 100.00宣传品36 56.5556 11.61881 1.93647 52.6243 60.4868 33.00 86.00 体验36 66.6111 13.49768 2.24961 62.0442 71.1781 37.00 87.00 总数144 66.8194 13.52783 1.12732 64.5911 69.0478 33.00 100.00多重比较销售额LSD(I) 广告形式(J) 广告形式均值差(I-J) 标准误显著性95% 置信区间下限上限报纸广播 2.33333 2.83846 .412 -3.2784 7.9451 宣传品16.66667* 2.83846 .000 11.0549 22.2784体验 6.61111* 2.83846 .021 .9993 12.2229 广播报纸-2.33333 2.83846 .412 -7.9451 3.2784 宣传品14.33333* 2.83846 .000 8.7216 19.9451体验 4.27778 2.83846 .134 -1.3340 9.8896 宣传品报纸-16.66667* 2.83846 .000 -22.2784 -11.0549 广播-14.33333* 2.83846 .000 -19.9451 -8.7216体验-10.05556* 2.83846 .001 -15.6673 -4.4438体验报纸-6.61111* 2.83846 .021 -12.2229 -.9993 广播-4.27778 2.83846 .134 -9.8896 1.3340宣传品10.05556* 2.83846 .001 4.4438 15.6673*. 均值差的显著性水平为0.05。

单因素方差分析实例[例6-8]在1990 年秋对“亚运会期间收看电视的时间”调查结果如下表所示。

问：收看电视的时间比平日减少了（第一组）、与平日无增减（第二组）、比平日增加了（第三组）的三组居民在“对亚运会的总态度得分”上有没有显著的差异？即要检验从“态度”上看，这三组居民的样本是取自同一总体还是取自不同的总体在SPSS 中进行方差分析的步骤如下：（1）定义“居民对亚运会的总态度得分”变量为X（数值型），定义组类变量为G（数值型），G=1、2、3 表示第一组、第二组、第三组。

然后录入相应数据，如图6-66所示图6-66 方差分析数据格式（2）选择[Analyze]=>[Compare Means]=>[One-Way ANOVA...]，打开[One-Way ANOVA]主对话框（如图6-67所示）。

从主对话框左侧的变量列表中选定X，单击按钮使之进入[Dependent List]框，再选定变量G，单击按钮使之进入[Factor]框。

单击[OK]按钮完成。

图6-67 方差分析对话框（3）分析结果如下：因此，收看电视时间不同的三个组其对亚运会的态度是属于三个不同的总体。

多因素方差分析[例6-11]从由五名操作者操作的三台机器每小时产量中分别各抽取1 个不同时段的产量，观测到的产量如表6-31所示。

试进行产量是否依赖于机器类型和操作者的方差分析。

SPSS 的操作步骤为：（1）定义“操作者的产量”变量为X（数值型），定义机器因素变量为G1（数值型）、操作者因素变量为G2（数值型），G1=1、2、3 分别表示第一、二、三台机器，G2=1、2、3、4、5 分别表示第1、2、3、4、5 位操作者。

录入相应数据，如图6-68所示。

图6-68 双因素方差分析数据格式（2）选择[Analyze]=>[General Linear Model]=>[Univariate...]，打开[Univariate]主对话框（如图6-69所示）。