OneWayANOVA单因素方差分析

单因素方差分析（one-wayANOVA）单因素⽅差分析（one-wayANOVA）单因素⽅差分析（⽅）单因素⽅差分析概念是⽅来研究⽅个控制变量的不同⽅平是否对观测变量产⽅了显著影响。

这⽅，由于仅研究单个因素对观测变量的影响，因此称为单因素⽅差分析。

例如，分析不同施肥量是否给农作物产量带来显著影响，考察地区差异是否影响妇⽅的⽅育率，研究学历对⽅资收⽅的影响等。

这些问题都可以通过单因素⽅差分析得到答案。

（⽅）单因素⽅差分析步骤第⽅步是明确观测变量和控制变量。

例如，上述问题中的观测变量分别是农作物产量、妇⽅⽅育率、⽅资收⽅；控制变量分别为施肥量、地区、学历。

第⽅步是剖析观测变量的⽅差。

⽅差分析认为：观测变量值的变动会受控制变量和随机变量两⽅⽅的影响。

据此，单因素⽅差分析将观测变量总的离差平⽅和分解为组间离差平⽅和和组内离差平⽅和两部分，⽅数学形式表述为：SST=SSA+SSE。

第三步是通过⽅较观测变量总离差平⽅和各部分所占的⽅例，推断控制变量是否给观测变量带来了显著影响。

（三）单因素⽅差分析原理总结在观测变量总离差平⽅和中，如果组间离差平⽅和所占⽅例较⽅，则说明观测变量的变动主要是由控制变量引起的，可以主要由控制变量来解释，控制变量给观测变量带来了显著影响；反之，如果组间离差平⽅和所占⽅例⽅，则说明观测变量的变动不是主要由控制变量引起的，不可以主要由控制变量来解释，控制变量的不同⽅平没有给观测变量带来显著影响，观测变量值的变动是由随机变量因素引起的。

（四）单因素⽅差分析基本步骤1、提出原假设：H0——⽅差异；H1——有显著差异2、选择检验统计量：⽅差分析采⽅的检验统计量是F统计量，即F值检验。

3、计算检验统计量的观测值和概率P值：该步骤的⽅的就是计算检验统计量的观测值和相应的概率P值。

4、给定显著性⽅平，并作出决策（五）单因素⽅差分析的进⽅步分析在完成上述单因素⽅差分析的基本分析后，可得到关于控制变量是否对观测变量造成显著影响的结论，接下来还应做其他⽅个重要分析，主要包括⽅差齐性检验、多重⽅较检验。

SPSS统计分析软件应用一、SPSS中的单因素方差分析(One-Way Anova) （一）基本原理单因素方差分析也即一维方差分析，是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题，如各组之间有显著差异，说明这个因素（分类变量）对因变量是有显著影响的，因素的不同水平会影响到因变量的取值。

（二）实验工具SPSS for Windows（三）试验方法例：某灯泡厂用四种不同配料方案制成的灯丝（filament），生产了四批灯泡。

在每批灯泡中随机地抽取若干个灯泡测其使用寿命（单位：小时hours），数据列于下表，现在想知道，对于这四种灯丝生产的灯泡，其使用寿命有无显著差异。

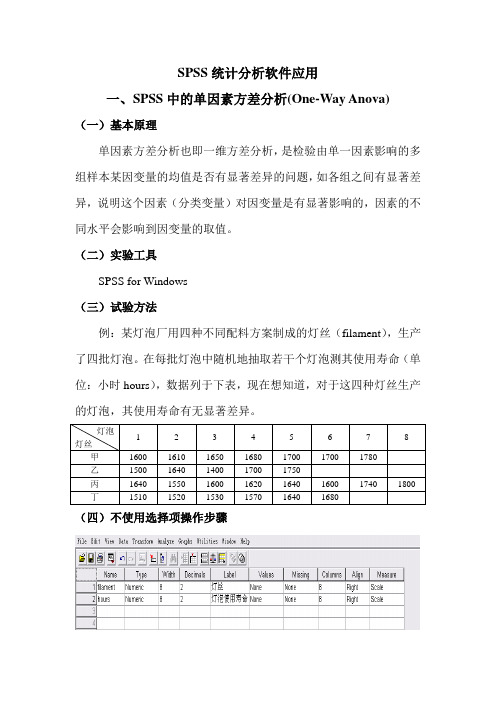
（四）不使用选择项操作步骤（1）在数据窗建立数据文件，定义两个变量并输入数据，这两个变量是：filament变量，数值型，取值1、2、3、4分别代表甲、乙、丙、丁，格式为F1.0，标签为“灯丝”。

Hours变量，数值型，其值为灯泡的使用寿命，单位是小时，格式为F4.0，标签为“灯泡使用寿命”。

（2）按Analyze，然后Compared Means，然后One-Way Anova 的顺序单击，打开“单因素方差分析”主对话框。

（3）从左边源变量框中选取变量hours，然后按向右箭头，所选去的变量hours即进入Dependent List框中。

（4）从左边源变量框中选取变量filament，然后按向右箭头，所选取的变量folament即进入Factor框中。

（5）在主对话框中，单击“OK”提交进行。

（五）输出结果及分析灯泡使用寿命的单因素方差分析结果该表各部分说明如下：第一列：方差来源，Between Groups是组间变差，Within Groups 是组内变差，Total是总变差。

第二列：离差平方和，组间离差平方和为39776.46，组内离差平方和为178088.9，总离差平方和为217865.4，是组间离差平方和与组内离差平方和相加而得。

Minitab单因素方差分析
什么是单因素方差分析？
单因素方差分析〔One-way ANOVA〕是统计学中一种常见的假设检
验方法，用于比拟多个组或处理之间的均值差异是否显著。

在许多实验和研究中，我们经常需要比拟不同组或处理条件下的平
均值是否存在显著差异。

这时，方差分析就是我们常用的工具之一。

在Minitab中，进行单因素方差分析非常简单。

如何在Minitab中进行单因素方差分析？
要在Minitab中进行单因素方差分析，我们需要先准备好要分析的
数据，并按照一定的格式输入到Minitab软件中。

下面是一个例如数据集，我们将使用这个数据集来进行后续的分析：
Treatment Value
Group 1 12.5
Group 1 10.8
Group 1 11.2
Group 1 9.5
Group 2 8.7
Group 2 9.2
Group 2 10.1
Group 2 11.3
Group 3 7.6
Group 3 8.2
Group 3 9.0
Group 3 10.5
在Minitab中，我们可以按照以下步骤进行单因素方差分析：
1.翻开Minitab软件，并导入数据集；
2.在菜单栏中选择。

真的！单因素方差分析你用错了！方差分析简介方差分析（analysis of variance,简写为ANOVA）是进行多个均数比较的常用方法。

这种方法的基本思路是通过对变异进行分解和分析，从而达到统计推断之目的。

由于该方法是由英国统计学家R.A.Fisher于1923年首先提出的，因此又称为F检验。

最简单的方差分析，就是单因素方差分析（one-way anova），用于分析含有一个分类变量、一个定量变量的资料，用于多个样本均数的比较中。

方差分析对原始数据的要求与t检验一样，即要求资料满足独立性、正态性和方差齐性。

来个判断题，求围观！！因为单因素方差分析要求资料满足方差齐、正态性的条件，故当方差齐或正态性的条件不满足且经过变量变换也不满足时，应当采用非参数检验（如Kruskal-Wallis test）。

这句话对吗？这是有些传统统计教材中的说法，但是我很负责任的告诉你，上面的观点是错误的。

近日，在国外生物统计学方法相关资料中发现了针对单因素方差分析不满足应用前提（正态性、方差齐）的推荐处理方法，完全颠覆了我的以往思路。

现总结归纳如下一、当资料不满足正态性，由于单因素方法分析结果对资料不满足正态性的情况并不敏感，仍推荐使用单因素方差分析，不推荐非参数检验（Kruskal-Wallis test）。

二、当资料不满足方差齐性，推荐采用Welch's ANOVA，不推荐非参数检验（Kruskal-Wallis test）。

下面详细解释为什么不推荐非参数检验（Kruskal-Wallis test）的原因。

1不满足正态性的情况当资料中含有一个分类变量、一个定量变量，我们常常采用单因素方差分析。

但当不同组中的定量变量不满足正态性的条件，Kruskal–Wallis test往往被人们用为替代方法。

因为他们认为除非样本量非常大并且满足正态分布，否则就应该采用Kruskal–Wallis test；而且当数据正态性的条件不满足时，使用单因素方差分析是错误和危险的。

SPSS中的单因素方差分析（One-Way Anova）SPSS中的单因素方差分析(One-Way Anova) 一、基本原理单因素方差分析也即一维方差分析，是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题，如各组之间有显著差异，说明这个因素(分类变量)对因变量是有显著影响的，因素的不同水平会影响到因变量的取值。

二、实验工具SPSS for Windows三、试验方法例:某灯泡厂用四种不同配料方案制成的灯丝(filament)，生产了四批灯泡。

在每批灯泡中随机地抽取若干个灯泡测其使用寿命(单位:小时hours)，数据列于下表，现在想知道，对于这四种灯丝生产的灯泡，其使用寿命有无显著差异。

灯泡 1 2 3 4 5 6 7 8 灯丝甲 1600 1610 1650 1680 1700 1700 1780乙 1500 1640 1400 1700 1750丙 1640 1550 1600 1620 1640 1600 1740 1800丁 1510 1520 1530 1570 1640 1680 四、不使用选择项操作步骤(1)在数据窗建立数据文件，定义两个变量并输入数据，这两个变量是:filament变量，数值型，取值1、2、3、4分别代表甲、乙、丙、丁，格式为F1.0，标签为“灯丝”。

Hours变量，数值型，其值为灯泡的使用寿命，单位是小时，格式为F4.0，标签为“灯泡使用寿命”。

(2)按Analyze，然后Compared Means，然后One-Way Anova的顺序单击，打开“单因素方差分析”主对话框。

(3)从左边源变量框中选取变量hours，然后按向右箭头，所选去的变量hours 即进入Dependent List框中。

(4)从左边源变量框中选取变量filament，然后按向右箭头，所选取的变量folament即进入Factor框中。

(5)在主对话框中，单击“OK”提交进行。

单因素方差分析范文单因素方差分析（One-way Analysis of Variance，简称ANOVA）是统计学中一种常用的方法，用于比较三个或三个以上的组的均值是否存在显著差异。

本篇文章将从原理、假设、步骤和应用等方面进行介绍。

一、原理二、假设在进行单因素方差分析时，需要假设组间均值是否存在显著差异。

具体的假设如下：H0：各组均值相等（即组间均值差异不显著）H1：至少有两组均值不相等（即组间均值差异显著）三、步骤进行单因素方差分析的步骤如下：1.根据研究目的和问题选择合适的统计方法；2.收集数据，涉及到多个组的测量值；3. 计算总平方和（SS_total），表示总变异性大小；4. 计算组间平方和（SS_between），表示组间变异性大小；5. 计算组内平方和（SS_within），表示组内变异性大小；6. 根据以上计算结果，计算组间均方（MS_between）和组内均方（MS_within）；7. 计算F值，即F=MS_between/MS_within；8.根据设定的显著性水平（通常为0.05），查表或计算得到临界值；9.比较计算得到的F值与临界值，判断是否达到显著性水平。

四、应用1.医学研究：比较不同药物对疾病治疗效果的影响；2.教育研究：比较不同教学方法对学生学习成绩的影响；3.市场调查：比较不同广告对产品销量的影响；4.农业实验：比较不同施肥方式对作物产量的影响。

五、总结单因素方差分析是一种常用的统计方法，通过比较三个或三个以上组的均值差异来判断各组之间是否存在显著差异。

它的优点是可以同时比较多个组均值的差异，从而提高实验效率和减少误判，应用广泛且实用。

因此，研究者在进行多组均值比较时，可以选择单因素方差分析方法进行分析。

单因素方差分析单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOVA过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表5-1所示。

表5-1 不同水稻品种百丛中稻纵卷叶螟幼虫数从复水稻品种1 2 3 4 51 41 33 38 37 312 39 37 35 39 343 40 35 35 38 34 数据保存在“DATA5-1.SAV”文件中，变量格式如图5-1。

图5-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

1）准备分析数据在数据编辑窗口中输入数据。

建立因变量“幼虫”和因素水平变量“品种”，然后输入对应的数值，如图5-1所示。

或者打开已存在的数据文件“DATA5-1.SAV”。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOVA”项，系统打开单因素方差分析设置窗口如图5-2。

图5-2 单因素方差分析窗口3）设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量:选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图5-3所示的对话框。

该对话框用于设置均值的多项式比较。

图5-3 “Contrasts”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图5-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。