下载文档原格式
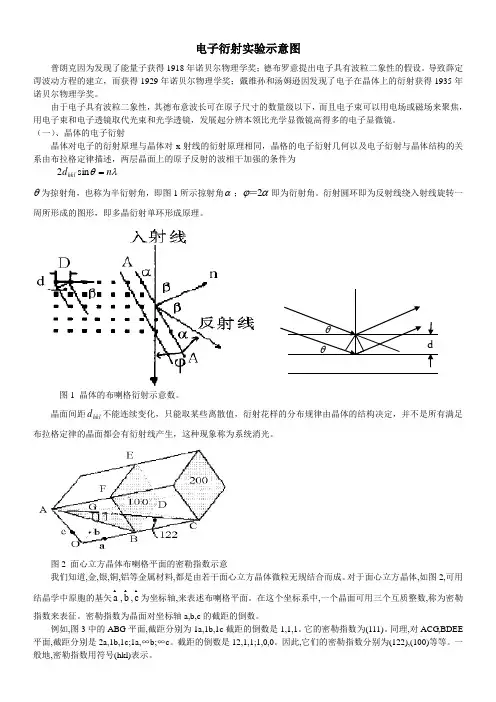
电子衍射实验示意图普朗克因为发现了能量子获得1918年诺贝尔物理学奖；德布罗意提出电子具有波粒二象性的假设。
导致薛定谔波动方程的建立，而获得1929年诺贝尔物理学奖；戴维孙和汤姆逊因发现了电子在晶体上的衍射获得1935年诺贝尔物理学奖。
由于电子具有波粒二象性，其德布意波长可在原子尺寸的数量级以下，而且电子束可以用电场或磁场来聚焦，用电子束和电子透镜取代光束和光学透镜，发展起分辨本领比光学显微镜高得多的电子显微镜。
（一）、晶体的电子衍射晶体对电子的衍射原理与晶体对x 射线的衍射原理相同，晶格的电子衍射几何以及电子衍射与晶体结构的关系由布拉格定律描述，两层晶面上的原子反射的波相干加强的条件为θ为掠射角，也称为半衍射角，即图1所示掠射角α；2ϕα＝即为衍射角。
衍射圆环即为反射线绕入射线旋转一周所形成的图形，即多晶衍射单环形成原理。
图1 晶体的布喇格衍射示意数。
晶面间距hkl d 不能连续变化，只能取某些离散值，衍射花样的分布规律由晶体的结构决定，并不是所有满足布拉格定律的晶面都会有衍射线产生，这种现象称为系统消光。
图2 面心立方晶体布喇格平面的密勒指数示意我们知道,金,银,铜,铝等金属材料,都是由若干面心立方晶体微粒无规结合而成。
对于面心立方晶体,如图2,可用结晶学中原胞的基矢a ,b ,c 为坐标轴,来表述布喇格平面。
在这个坐标系中,一个晶面可用三个互质整数,称为密勒指数来表征。
密勒指数为晶面对坐标轴a,b,c 的截距的倒数。
例如,图3中的ABG 平面,截距分别为1a,1b,1c 截距的倒数是1,1,1。
它的密勒指数为(111)。
同理,对ACG ,BDEE 平面,截距分别是2a,1b,1c;1a,∞b;∞c 。
截距的倒数是12,1,1;1,0,0。
因此,它们的密勒指数分别为(122),(100)等等。
一般地,密勒指数用符号(hkl)表示。
λθn d hkl =sin 2例如，对于立方晶系的晶体，222l k h ad hkl ++= ，a 为晶格常数（晶格平移基矢量的长度），是包含晶体全部对称性的、体积最小的晶体单元——单胞的一个棱边的长度。
