下载文档原格式
大学物理教案：量子力学基础知识简介量子力学是现代物理学的重要分支，它描述了微观世界中的粒子行为，并解释了许多奇特的现象。
本教案旨在向大学物理学生介绍量子力学的基础知识，包括波粒二象性、不确定性原理、波函数等核心概念。
目标•理解波粒二象性的概念及其实验观测•掌握不确定性原理及其与经典物理的区别•熟悉波函数的表示和应用教学内容1. 波粒二象性•定义：波粒二象性指微观粒子既具有粒子性质又具有波动性质。
•实验观测：通过双缝干涉实验、康普顿散射实验证明波粒二象性。
•特征：粒子表现出波动行为，如干涉和衍射；波动表现出离散行为，如能级和量子跳跃。
2. 不确定性原理•定义：不确定性原理是由海森堡提出的一个基本原理，它指出在某些物理量之间存在固有的不确定关系。
•区别于经典物理：经典物理中，粒子的位置和动量可以同时被准确测量；而在量子力学中，由于波粒二象性，位置和动量不能同时被准确确定。
•数学表述：∆x * ∆p ≥ h/4π，其中∆x表示位置的不确定性，∆p表示动量的不确定性，h为普朗克常数。
3. 波函数•定义：波函数是描述微观粒子状态及其演化的数学函数。
在薛定谔方程下演化。
•形式：一维情况下可用复数函数表示ψ(x)，三维情况下可用复数函数表示ψ(x, y, z)。
•解释与应用：波函数的平方模值|ψ|^2 表征了粒子在空间中存在的概率分布。
波函数可以描述能级、态叠加等现象。
教学方法与活动建议1.通过实验演示双缝干涉实验，让学生亲身体验波粒二象性。
2.运用黑板或幻灯片展示不确定性原理的公式推导过程，并举例说明其应用。
3.利用计算机模拟软件绘制波函数的图像，让学生观察不同态的波函数变化。
4.在课堂上进行小组讨论和问题解答，加深学生对概念和原理的理解。
总结通过本教案，学生将能够初步了解量子力学中重要的基础知识。
这些核心概念对于理解量子物理现象以及后续相关课程的学习都具有重要意义。
在教学过程中，鼓励学生积极思考并提出问题，以促进他们对量子力学的兴趣和深入理解。
大学物理 量子物理基础知识点1.黑体辐射（1）黑体：在任何温度下都能把照射在其上所有频率的辐射全部吸收的物体。
（2）斯特藩—玻尔兹曼定律：4o M T T σ（）= （3）维恩位移定律：m T b λ= 2.普朗克能量量子化假设（1）普朗克能量子假设：电磁辐射的能量是由一份一份组成的，每一份的能量是：h εν= 其中h 为普朗克常数，其值为346.6310h J s -=⨯⋅ （2）普朗克黑体辐射公式：2521M T ()1hckthc eλπλλ=-（,）3.光电效应和光的波粒二象性（1）遏止电压a U 和光电子最大初动能的关系为：212a mu eU = （2）光电效应方程： 212h mu A ν=+ （3）红限频率：恰能产生光电效应的入射光频率： 00V A K hν== （4）光的波粒二象性（爱因斯坦光子理论）：2mc hεν==；hp mc λ==；00m =其中0m 为光子的静止质量，m 为光子的动质量。
4.康普顿效应： 00(1cos )hm cλλλθ∆=-=- 其中θ为散射角，0m 为光子的静止质量，1200 2.42610hm m cλ-==⨯，0λ为康普顿波长。
5.氢原子光谱和玻尔的量子论： （1）里德伯公式: ()22111T T HR m n n m m nνλ==-=->（）()(), （2）频率条件: k nkn E E hν-=(3) 角动量量子化条件：,1,2,3...e L m vr n n ===其中2hπ=，称为约化普朗克常量，n 为主量子数。
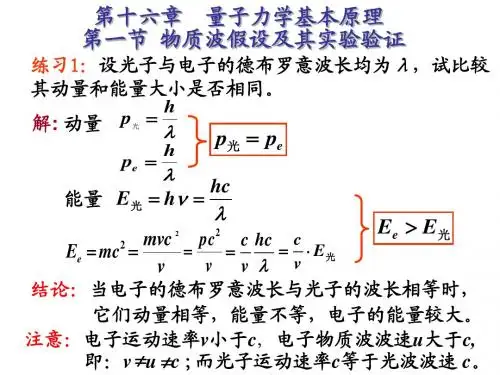
（4）氢原子能量量子化公式： 12213.6n E eVE n n=-=- 6.实物粒子的波粒二象性和不确定关系（1）德布罗意关系式： h h p u λμ== （2）不确定关系: 2x p ∆∆≥； 2E t ∆∆≥7.波函数和薛定谔方程（1）波函数ψ应满足的标准化条件：单值、有限、连续。
（2）波函数的归一化条件: (,)(,)1Vr t r t d ψψτ*=⎰（3）波函数的态叠加原理: 1122(,)(,)(,)...(,)iiir t c r t c r t c r t ψψψψ=++=∑（4）薛定谔方程: 22(,)()(,)2i r t U r r t t ψψμ⎡⎤∂=-∇+⎢⎥∂⎣⎦8.电子自旋和原子的壳层结构（1）电子自旋： 11),2S s ==；1,2z s s S m m ==±注：自旋是一切微观粒子的基本属性. （2）原子中电子的壳层结构①原子核外电子可用四个量子数(,,,l s n l m m )描述：主量子数：0,1,2,3,...n = 它主要决定原子中电子的能量。
大学物理理论：量子力学基础1. 介绍量子力学是现代物理学的重要分支，它描述了微观粒子的行为和性质。
本文将介绍一些关于量子力学的基本概念和原理。
2. 原子结构和波粒二象性2.1 光电效应光电效应实验证明了光具有粒子性。
解释光电效应需要引入光量子（光子）概念，并讨论能量、动量和波长之间的关系。
2.2 德布罗意假设德布罗意假设认为微观粒子也具有波动性。
通过计算微观粒子的德布罗意波长，可以得出与经典物理不同的结果。
3. 波函数和不确定性原理3.1 波函数及其统计解释波函数描述了一个系统的状态，并包含了关于该状态各个可观测量的信息。
通过波函数，可以计算出一系列平均值，用来描述系统的特征。
3.2 不确定性原理不确定性原理指出，在某些情况下，无法同时准确地确定一个粒子的位置和动量。
这涉及到测量的本质和粒子与波的性质之间的关系。
4. 玻尔模型和量子力学4.1 玻尔模型玻尔模型是描述氢原子中电子运动的经典物理学模型。
它通过量子化角动量来解释氢原子光谱，并提供了首个对原子结构和能级分布的定性解释。
4.2 泡利不相容原理泡利不相容原理说明电子在同一能级上必须具有不同的状态。
这为填充多电子原子如何达到稳态提供了解释。
5. 薛定谔方程及其解析方法5.1 薛定谔方程薛定谔方程是量子力学中最基本的方程。
它描述了波函数随时间演化的规律，以及如何通过波函数求得可观测量的平均值。
5.2 解析方法介绍几种求解薛定谔方程的解析方法，如分离变量法、变换法等，并通过示例问题演示其使用过程和计算结果。
6. 哈密顿算符与算符方法6.1 哈密顿算符哈密顿算符是用于描述系统总能量的数量。
介绍哈密顿算符的概念和性质，并讨论如何通过其本征值和本征函数求解问题。
6.2 算符方法算符是量子力学中描述可观测量的数学工具，介绍常见的一些算符，如位置算符、动量算符等，并讨论它们之间的对易关系。
结论量子力学作为现代物理学的基石，为我们理解微观世界提供了全新的视角。
量子物理知识点总结大学一、基本概念1. 波粒二象性在量子物理中，粒子表现出了波动性。
这意味着粒子不仅可以像经典物理学中的粒子那样具有位置和动量，还可以像波动那样传播。
这一现象成为波粒二象性。
著名的实验有双缝干涉实验，它展示了粒子具有波动性的特征。
2. 不确定性原理不确定性原理是量子物理的核心概念之一，由著名的物理学家海森堡提出。
它表明，对于一对共轭的物理量（比如位置和动量），我们无法同时精确地知道它们的数值。
如果我们知道其中一个量的值，那么对于另一个量，我们就无法确定其精确数值，并且只能知道其可能的取值范围。
这个原理对于解释微观世界中的许多现象都是非常重要的。
3. 物理量的量子化在经典物理中，我们习惯于将物理量看作是连续变化的，比如位置、速度、能量等。
然而在量子物理中，这些物理量被发现是离散的，只能取某些特定的数值，这一现象被称为量子化。
比如，电子只能存在于特定的能级上，能量也只能以量子的形式发射和吸收。
4. 相互作用的量子描述在经典物理中，我们常常通过描述相互作用的力来理解物质世界。
然而在量子物理中，力被描述为一种粒子交换的过程。
例如，电磁力是通过光子的交换传递的，强核力是通过胶子的交换传递的。
5. 观察者效应在量子物理中，观察者的存在和观察行为会影响到物质的状态和行为。
这一现象是被称为观察者效应。
具体来说，当我们观察量子粒子时，它的行为会因观察者的观察方式而发生变化。
二、量子力学1. 薛定谔方程薛定谔方程是量子力学中最基本的方程之一，描述了量子系统的演化。
它是线性、时间反演不变的方程，描述了量子系统的波函数随时间的演化。
通过薛定谔方程，我们可以预测量子系统在未来的状态。
2. 波函数和概率波在量子力学中，我们用波函数来描述粒子的状态。
波函数是一个数学函数，它包含了粒子的全部信息。
通过波函数，我们可以计算出粒子在不同位置和动量上的概率分布。
这个概率分布被称为概率波。
3. 微扰理论微扰理论是量子力学中的一种重要的近似计算方法，它被用于处理那些无法通过精确解析方法进行求解的问题。
