张正友相机标定算法

张正友标定算法原理详解
张正友标定算法是一种多摄像机标定的有效方法，它使用了一个具有内部参考点的3D物体来检测至少6个相互独立的2D-3D配准，从而确定每个摄像机之间的关系。

该算法的优点在于它能够利用棋盘格子上的多个点，从而使得标定更加可靠。

张正友标定算法主要分为三步：
(1)首先获取所有摄像机的内参和外参，这些参数表示每个摄像机的视角和位置，包括焦距、畸变参数和旋转参数等信息。

(2)计算每个摄像机的平面坐标系，这些平面坐标系将求解的不同摄像机之间的关系。

(3)把实际的物体点映射到每个摄像机的平面坐标系中，并计算所有摄像机之间的关系。

最后，张正友标定算法可以得出每个摄像机的位置和姿态，从而实现多摄像机视角的标定。

张正友相机标定算法解读一直以来想写篇相机标定方面的东西，最近组会上也要讲标定方面东西，所以顺便写了。

无论是OpenCV还是matlab标定箱，都是以张正友棋盘标定算法为核心实现的,这篇PAMI的文章《A Flexible New Technique for Camera Calibration》影响力极大，张正友是浙江大学的机械系出身，貌似现在是微软的终身教授了。

我就简单的介绍下算法的核心原理，公式的推理可能有点多。

一基本问题描述：空间平面的三维点与相机平面二维点的映射。

假设空间平面中三维点：（齐次坐标，世界坐标系）。

相机平面二维点：（齐次坐标，相机坐标系）。

那么空间中的点是如何映射到相机平面上去呢？我们用一个等式来表示两者之间关系：（1）注：A为相机内参矩阵，R，t分别为旋转和平移矩阵，s为一个放缩因子标量。

我们把等式（1）再简化下：（2）因为张正友算法选取的是平面标定，所以令z=0,所以平移向量只有r1,r2即可。

H就是我们常说的单应性矩阵，在这里描述的是空间中平面三维点和相机平面二维点之间的关系。

因为相机平面中点的坐标可以通过图像处理的方式（哈里斯角点，再基于梯度搜索的方式精确控制点位置）获取，而空间平面中三维点可以通过事先做好的棋盘获取。

所以也就是说每张图片都可以计算出一个H矩阵。

二内参限制我们把H矩阵(3*3)写成3个列向量形式，那么我们把H矩阵又可写成：（3)注:lamda是个放缩因子标量，也是s的倒数。

那么现在我们要用一个关键性的条件：r1和r2标准正交。

正交：（4）单位向量（模相等）：（5）这个两个等式是非常优美的，因为它完美的与绝对二次曲线理论联系起来了，这里就不展开了。

三相机内参的求解我们令：（6）我们可知B矩阵是个对称矩阵，所以可以写成一个6维向量形式：（7）我们把H矩阵的列向量形式为：（8）那么根据等式（8）我们把等式（4）改写成：（9）（10）最后根据内参数限制条件(等式（4）(5)):(11)即,(12)V矩阵是2*6矩阵，也就是说每张照片可建立起两个方程组，6个未知数。

张正友标定法是相机标定中常用的一种方法，通过该方法可以实现相机内外参数的标定。

在使用张正友标定法进行相机标定时，需要编写相应的matlab代码来实现算法。

下面将介绍如何使用matlab实现张正友标定法，并给出相应的matlab代码。

1. 准备标定板图像首先需要准备一组包含标定板的图像，标定板上应具有特定的特征点，例如棋盘格。

这些图像将用于计算相机的内外参数。

2. 读取标定板图像使用matlab的imread函数读取准备好的标定板图像，将图像存储为一个cell数组。

```matlabimages = cell(1,N);for i = 1:Nfilename = ['image',num2str(i),'.jpg'];images{i} = imread(filename);end```3. 提取标定板角点利用matlab的detectCheckerboardPoints函数提取标定板图像中的角点坐标，将提取的角点保存到一个cell数组中。

```matlabimagePoints = cell(1, N);for i = 1:NI = images{i};[imagePoints{i}, boardSize] = detectCheckerboardPoints(I); end```4. 标定相机参数使用matlab的estimateCameraParameters函数对提取的角点进行相机参数标定，得到相机的内外参数。

```matlab[cameraParams, imagesUsed, estimationErrors] = estimateCameraParameters(imagePoints, worldPoints,'EstimateSkew', true, 'EstimateTangentialDistortion', true);```5. 查看标定结果可以利用标定得到的相机参数对新的图像进行矫正，并查看标定结果的精度。

相机标定算法的源代码相机标定是计算机视觉领域中的一项重要技术，它用于确定相机的内部参数和外部参数，以便将相机采集到的图像转换为真实世界的坐标。

在计算机视觉和机器人领域中，相机标定是一项关键工作。

相机标定的主要目的是确定相机的内参矩阵（包括焦距、主点位置等）和外参矩阵（包括相机的位置和方向）。

通过相机标定，我们可以校正图像畸变并获得准确的三维坐标。

相机标定算法的本质是寻找一个数学模型来描述相机成像过程。

其中，最常用的相机标定算法是张正友标定算法（Zhang'scalibration algorithm）。

该算法基于已知的二维图像和三维世界点之间的对应关系，通过最小化重投影误差来估计相机的内外参数。

具体而言，张正友标定算法首先需要采集一组已知的二维图像和对应的三维世界点。

然后，通过对这些对应点进行特征提取和匹配，可以得到相机坐标系下的图像坐标和世界坐标系下的三维点坐标。

接下来，通过最小二乘法求解相机的内外参数。

在具体实现中，张正友标定算法通常利用棋盘格图案作为标定板，因为棋盘格具有明显的特征点，易于提取和匹配。

在标定过程中，需要在不同的位置和姿态下采集多张棋盘格图像，并提取出角点的二维坐标。

通过这些角点的二维坐标和已知的三维世界坐标，可以使用最小二乘法求解出相机的内外参数。

另外，除了张正友标定算法外，还有其他一些常用的相机标定算法，如Tsai算法和Matlab自带的相机标定工具箱。

这些算法在实现上可能有一些差异，但都基于类似的原理，即通过已知的二维和三维对应关系来求解相机参数。

总结起来，相机标定是计算机视觉中的重要技术之一，它通过寻找数学模型来描述相机成像过程，从而获得准确的相机内外参数。

其中，张正友标定算法是最常用的相机标定算法之一，通过最小化重投影误差来求解相机的内外参数。

在实际应用中，相机标定算法可以用来校正图像畸变、恢复三维场景的几何结构等，具有广泛的应用前景。

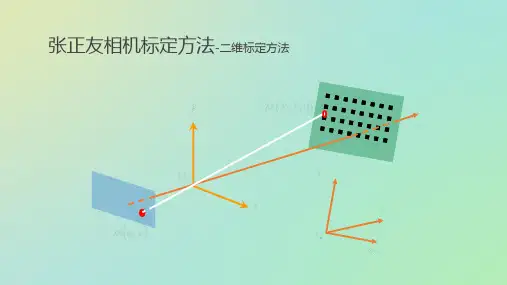
SLAM ⼊门之视觉⾥程计（6）：相机标定张正友经典标定法详解想要从⼆维图像中获取到场景的三维信息，相机的内参数是必须的，在SLAM 中，相机通常是提前标定好的。

张正友于1998年在论⽂："A Flexible New Technique fro Camera Calibration"提出了基于单平⾯棋盘格的相机标定⽅法。

该⽅法介于传统的标定⽅法和⾃标定⽅法之间，使⽤简单实⽤性强，有以下优点：不需要额外的器材，⼀张打印的棋盘格即可。

标定简单，相机和标定板可以任意放置。

标定的精度⾼。

相机的内参数设P =(X ,Y ,Z )为场景中的⼀点，在针孔相机模型中，其要经过以下⼏个变换，最终变为⼆维图像上的像点p =(µ,ν):1. 将P 从世界坐标系通过刚体变换(旋转和平移)变换到相机坐标系，这个变换过程使⽤的是相机间的相对位姿，也就是相机的外参数。

2. 从相机坐标系，通过透视投影变换到相机的成像平⾯上的像点p =(x ,y )。

3. 将像点p 从成像坐标系，通过缩放和平移变换到像素坐标系上点p =(µ,ν)。

相机将场景中的三维点变换为图像中的⼆维点，也就是各个坐标系变换的组合，可将上⾯的变换过程整理为矩阵相乘的形式：s µν1=α0c x 0βc y1f 0000f 0001R t 0T1X Y Z1=f x 0c x 00f yc y 001Rt 0T1X Y Z1将矩阵K 称为相机的内参数,K =f x0c x 0f yc y 001其中，α,β表⽰图像上单位距离上像素的个数，则f x =αf ,f y =βf 将相机的焦距f 变换为在x,y ⽅向上像素度量表⽰。

另外，为了不失⼀般性，可以在相机的内参矩阵上添加⼀个扭曲参数γ，该参数⽤来表⽰像素坐标系两个坐标轴的扭曲。

则内参数K 变为K =f xγc x 0f yc y 01对于⼤多数标准相机来说，可将扭曲参数γ设为0. Multiple View Geometry in Computer Vision张⽒标定法在上⼀篇博⽂，介绍的单应矩阵表⽰两个平⾯间的映射。