巅峰对决专题一数与式(第二轮)

2019版高考数学二轮复习第一部分方法、思想解读专题对点练4 从审题中寻找解题思路文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2019版高考数学二轮复习第一部分方法、思想解读专题对点练4 从审题中寻找解题思路文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2019版高考数学二轮复习第一部分方法、思想解读专题对点练4 从审题中寻找解题思路文的全部内容。

专题对点练4 从审题中寻找解题思路一、选择题1.已知方程=1表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（ ）A 。

（—1,3）B 。

（-1，） C.（0，3) D.(0,）2.已知f (x )是R 上最小正周期为2的周期函数，且当0≤x 〈2时，f (x ）=x 3-x ，则函数y=f (x ）的图象在区间[0,6］上与x 轴的交点的个数为( ) A 。

6 B .7 C .8 D 。

9 3.已知F 1,F 2是双曲线C ：=1（a 〉0，b>0）的两个焦点,P 是C 上一点,若|PF 1|+|PF 2｜=6a ,且△PF 1F 2最小的内角为30°，则双曲线C 的渐近线方程是( ）A 。

x±y=0B .x±y=0C 。

x±2y=0D .2x±y=0 4.已知双曲线C :x 2—=1，过点P （1，1）作直线l ，使l 与C 有且只有一个公共点,则满足上述条件的直线l 的条数共有（ ) A 。

3 B 。

2 C .1 D 。

45。

已知二次函数f (x ）=ax 2+bx+c ,其中b>a ，且对任意x ∈R 都有f （x )≥0,则M=的最小值为（ )A .B .C 。

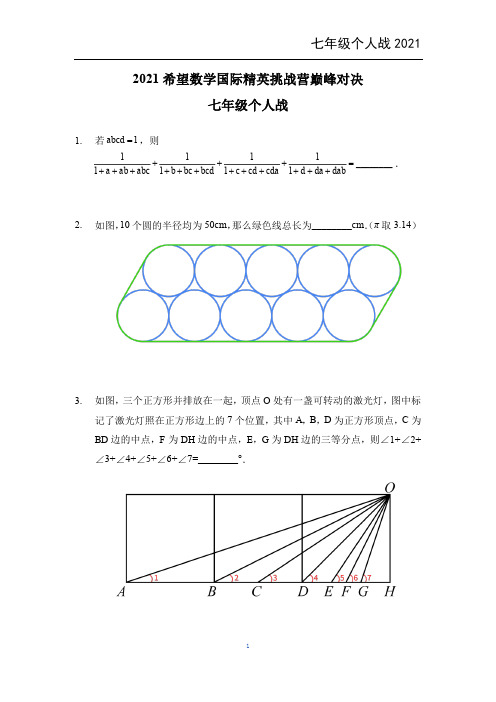
2021希望数学国际精英挑战营巅峰对决七年级个人战1.若1abcd =，则1111________1111a ab abc b bc bcd c cd cda d da dab+++=++++++++++++．2.如图，10个圆的半径均为50cm ，那么绿色线总长为________cm ．（π取3.14）3.如图，三个正方形并排放在一起，顶点O 处有一盏可转动的激光灯，图中标记了激光灯照在正方形边上的7个位置，其中A ，B ，D 为正方形顶点，C 为BD 边的中点，F 为DH 边的中点，E ，G 为DH 边的三等分点，则∠1+∠2+∠3+∠4+∠5+∠6+∠7=________°．4.若1+p 为质数，6+p 也为质数，则 ( p 2021+1)( p 2021 – 1) =________．5.汽车的速度是每小时54千米，出发时汽车里程表的示数末三位为abc ，行驶了若干小时（整数）后，汽车里程表的示数末三位数正好为cba ，其他数位上的数字没有变化，则汽车行驶了________小时．6.一个六位数的数字和与数字积相乘得到390．这样的六位数中，最大的一个与最小的一个相加，和是________．7.方程20212202122021(2)(2)2x x +--=的解为x =（ ）． A.22- B.12- C.1D.2E.228.________=．9.若222224620149100x t t t t =++++----，()()()()()()11111029101y t t t t t t =+++-+-+-+，则xy=________． 10.满足ab 2=610的正整数对（a ，b ）共有________对．11.定义运算：(,)f x y xy =(,)1x yg x y xy-=+， 如果34209,345525,55f g λ⎛⎫-= ⎪⎛⎫⎝⎭ ⎪⎝⎭，则λ=_________．12.满足125x +3y =2021的正整数组（x ，y ）有_________组．13.如图，点P 是正方形ABCD 的外接圆上一点．若2222PA PB PC PD +++=100，则正方形ABCD 的边长为_________．14.最初有47张扑克牌叠在一起，按照从上往下的顺序操作：将第一张和第二张扔掉，再将第三张放在最下面；将第四张和第五张扔掉，再将第六张放在最下面；将第七张和第八张扔掉，再将第九张放在最下面……直到最后只剩一张牌，这张牌最初是从上到下的第________张．15.舒克、贝塔周六早上9：00~9：30分别随机到达公园门口，他们到达时间至少相差10分钟的概率为（ ）．A.19B.29C.13D.49E.2316.如图，在平面直角坐标系中，O 为坐标原点，A （0，4），B （4，4），C （6，0），梯形OABC 内有一点P ．若△OAP 与△PBC 的面积比为1∶4，△ABP 与△OCP 的面积比为2∶3，则P 的坐标是（ ）．A.()12，B.()22，C. 423⎛⎫⎪⎝⎭， D. 4833⎛⎫⎪⎝⎭， E. 433⎛⎫⎪⎝⎭，17.一个五位数能被2025整除，且商恰好是这个五位数的各位数字的和，这样的五位数共有_________个．18.如左图，红黄蓝三枚棋子依次排列．现要把它们都向右移动三格，如右图．如果每次只能向右移动一枚棋子到相邻的空的格子中，那么共有________种不同的移动方案．19.小明将n本不同的书全部分给小希、小望和小乐三人，共有30种不同的分法．其中，小希分得1本，小望分得2本，小乐分得________本．20.已知[]x表示不超过x的最大整数，如[1.5]=1，[2]=2，则20406010103⎡⎤⎢⎥-⎣⎦的末两位数是________．答案。

高考数学第二轮教案模板教案标题：高考数学第二轮教案模板教学目标：1. 理解高考数学第二轮考试的要求和题型分布。

2. 熟悉解答高考数学第二轮考试中的各类题目的方法和技巧。

3. 提高学生的解题能力和应试水平。

教学内容：1. 复习和巩固高中数学重点知识点，包括概率、函数、三角函数、导数等内容。

2 了解高考数学第二轮考试的题型和难度分布。

3. 分析和掌握解答高考数学第二轮考试中的典型题目的解题方法和策略。

教学过程：一、导入（5分钟）通过复习一些基本的概念和方法引入今天的教学内容，让学生重新温习相关的知识点，并激发他们的学习兴趣。

二、介绍高考数学第二轮考试（10分钟）向学生介绍高考数学第二轮考试的大致分值分布和题型，以及这些题目所涉及的知识点和解题思路。

同时，解释考试中常见的易错点和解题陷阱，帮助学生避免在考试中犯类似错误。

三、讲解典型题目解题方法（30分钟）选择一些典型的高考数学第二轮考试题目进行详细的讲解和分析，包括题目的解题思路、关键步骤、常用方法和技巧等。

通过这些例题的讲解，帮助学生理解题目的解题思路和方法，并学会运用到实际的解题过程中。

四、练习与讨论（25分钟）组织学生进行相关的练习题目，在练习中学生可以自主解题，或小组合作解答。

鼓励学生互相讨论、交流解题思路，并引导他们思考不同解法的优缺点。

五、总结与反思（10分钟）针对今天的教学内容进行总结，帮助学生梳理重点和难点，回顾解题方法和策略。

同时，鼓励学生提出问题和疑惑，并进行解答和讨论，以加深学生对知识的理解和掌握。

六、作业布置（5分钟）布置与今天教学内容相关的作业，以巩固学生的学习成果和拓展他们的解题能力。

鼓励学生在独立完成作业的过程中，能够灵活运用所学的方法和技巧。

教学示范：教师在教学过程中可以通过多媒体、板书、讲解和讨论等方式进行教学。

在解题过程中，教师可以给学生提供一些提示和引导，使学生能够更好地理解和掌握解题方法。

教学评估：可以通过课堂练习和讨论中的学生表现来评估他们对教学内容的理解和掌握程度。

2023巅峰对决数学七下单元章末卷(教用)介绍本章末卷是为数学七下单元巅峰对决而设计的，用于巩固学生在本单元所学的知识与技能。

本文档旨在为教师提供一份完整的可打印版教学材料，方便教学使用。

目录1.第一章: 整数– 1.1 整数的概念– 1.2 整数的运算法则– 1.3 整数的应用2.第二章: 分数– 2.1 分数的基本概念– 2.2 分数的运算法则– 2.3 实际问题中的应用3.第三章: 代数式与方程式– 3.1 代数式的概念与性质– 3.2 代数式的化简与展开– 3.3 一元一次方程式的解法4.第四章: 图形的初步认识– 4.1 几何图形的分类– 4.2 平面图形的性质与判断– 4.3 几何图形的周长与面积计算5.第五章: 数据的收集整理和图表的运用– 5.1 数据的收集和整理– 5.2 图表的绘制和分析– 5.3 实际问题中的应用使用说明•请教师在使用前仔细阅读章节内容，确保了解每个章节所涉及的知识点和技能要求。

•每个章节可以单独打印，并根据需要进行调整和组合，适应不同的教学需求。

•每个章节下方附带了一些练习题，供学生进行巩固训练。

示例第一章: 整数1.1 整数的概念整数是数学中的一个重要概念。

从小学开始，学生就接触到了自然数和零，而整数的引入是为了更好地描述数轴上的数。

整数包括自然数、零和它们的相反数。

比如，整数2和整数-2就是一对相反数。

示例题:1.判断下列数中哪些是整数：–2–-0.5–0–-100练习题:1.计算下列整数的相反数：–8–-20–02.比较下列整数的大小：–5和-5–-10和-8–0和71.2 整数的运算法则整数之间的运算包括加法、减法、乘法和除法。

在进行整数运算时，需要遵循一定的法则和规则。

比如，两个正整数相加的结果仍然是正整数，而两个负整数相加的结果则是负整数。

示例题:1.计算下列整数的和：– 3 + 7–-5 + 2–-10 + (-3)练习题:1.计算下列整数的差：– 5 - 3–-7 - 2–-10 - (-3)2.计算下列整数的积：– 4 × 2–-5 × 3–-10 × (-2)1.3 整数的应用整数在实际生活中有广泛的应用。

2022巅峰对决数学第二轮答案1、14．平面上有三个点A，B，C，如果AB＝8，AC＝5，BC＝3，则（）[单选题] *A．点C在线段AB上(正确答案)B．点C在线段AB的延长线上C．点C在直线AB外D．不能确定2、已知10?＝5，则100?的值为( ) [单选题] *A. 25(正确答案)B. 50C. 250D. 5003、3.检验4个工作，其中超出标准质量的克数记作正数，不足标准质量的克数记作负数，则最接近标准质量的克数是（）[单选题] *A.4B.3C.-1(正确答案)D.-24、计算的结果是( ) [单选题] *A. -p2?(正确答案)B. p2?C. -p1?D. p1?5、以A（3，2），B（6，5），C（1，10）为顶点的三角形是（）[单选题] *A、锐角三角形B、锐角三角形C、直角三角形(正确答案)D、无法判断6、3．(2020·新高考Ⅰ，1,5分)设集合A={x|1≤x≤3}，B={x|2<x<4}，则A∪B=( ) [单选题] * A．{x|2<x≤3}B．{x|2≤x≤3}C．{x|1≤x<4}(正确答案)D．{x|1<x<4}7、f（x）=-2x+5在x=1处的函数值为（）[单选题] *A、-3B、-4C、5D、3(正确答案)8、下列计算正确的是( ) [单选题] *A. (－a)·(－a)2·(－a)3＝－a?B. (－a)·(－a)3·(－a)?＝－a?C. (－a)·(－a)2·(－a)?＝a?D. (－a)·(－a)?·a＝－a?(正确答案)9、14、在等腰中，如果的长是的2倍，且三角形周长为40，那么的长是（）[单选题] *A．10B．16 (正确答案)C．10D．16或2010、25．从五边形的一个顶点出发，可以画出m条对角线，它们将五边形分成n个三角形．则m、n的值分别为（）[单选题] *A．1，2B．2，3(正确答案)C．3，4D．4，411、从3点到6点，时针旋转了多少度？[单选题] *60°-90°(正确答案)-60°90°12、5.在数轴上点A，B分别表示数-2，-5，则A，B两点之间的距离可表示为（）[单选题] *A.-2+(-5)B.-2-(-5)(正确答案)C.(-5)+2D(-5)-213、16.5-（-3）-2的计算结果为（）[单选题] *A.3B.4C.0D.6(正确答案)14、代数式a3?a2化简后的结果是（）[单选题] *A. aB. a?(正确答案)C. a?D. a?15、46、在直角三角形ABC中，，，则的三条高之和为（）[单选题] * A．8.4B．9.4(正确答案)C．10.4D．11.16、两数之和为负数，则这两个数可能是? [单选题] *A.都是负数B.0和负数(正确答案)C.一个正数与一个负数D.一正一负或同为负数或0和负数17、27.下列各函数中，奇函数的是（）[单选题] *A. y=x^(-4)B. y=x^(-3)(正确答案)C .y=x^4D. y=x^(2/3)18、36．如果x2﹣kxy+9y2是一个完全平方式，那么k的值是（）[单选题] * A．3B．±6(正确答案)C．6D．±319、下列说法中，正确的是[单选题] *A.一个有理数不是正数就是负数(正确答案)B.正分数和负分数统称分数C.正整数和负整数统称整数D.零既可以是正整数也可以是负整数20、13．设x∈R，则“x3（x的立方）>8”是“|x|>2”的( ) [单选题] * A．充分而不必要条件(正确答案)B．必要而不充分条件C．充要条件D．既不充分也不必要条件21、19.下列函数在（0，+?? ）上为增函数的是（）. [单选题] *A.?（x）＝-xB.?（x）=-1/X(正确答案)C.?（x）=-x2D.?（x）=1/X22、下列计算正确是（）[单选题] *A. 3x﹣2x=1B. 3x+2x=5x2C. 3x?2x=6xD. 3x﹣2x=x(正确答案)23、31、点A(-2,-3)关于y轴对称的点的坐标是（）[单选题] * (2,3)(-2,-3)(3,-2)(2,-3) (正确答案)24、下列各对象可以组成集合的是（）[单选题] *A、与1非常接近的全体实数B、与2非常接近的全体实数(正确答案)C、高一年级视力比较好的同学D、与无理数相差很小的全体实数25、34、根据下列已知条件, 能画出唯一的△ABC的是（) [单选题] *A、∠C=90°，AB＝８，BC＝１0B、AB＝４，BC＝３，∠A＝３０°C、AB＝３，BC＝４，CA＝８D、∠A＝６０°，∠B＝４５°，AB＝６(正确答案)26、-330°是第（）象限角？[单选题] *第一象限(正确答案)第二象限第三象限第四象限27、6．若一个正比例函数的图象经过点(2，－3)，则这个图象一定也经过点( ) [单选题]* A．(－3，2)B．( 3/2，－1)C．(2/3，－1)(正确答案)D．( －2/3，1)28、6．已知集合A={0,1,2}，则集合B={(x，y)|x≥y，x∈A，y∈A}中元素的个数是( ) [单选题] *A．1B．3C．6(正确答案)D．929、8.如果直角三角形的三条边为2，4，a，那么a的取值可以有（）[单选题] *A. 0个B. 1个C. 2个D. 3个(正确答案)30、已知直线l的方程为2x-y+7=0，（）是直线l上的点[单选题] *A、（2，3）B、（2，4）(正确答案)C、（2，-3）D、（-2，-3）。

专题五 规律探索【中考命题趋势】猜想规律的相关题目在中考中一直被命题者所重视，其中包括数与式的规律探索、图形的规律探索、数形结合的规律探索.猜想规律型的问题难度相对较小，经常以选择题的形式出现，解题时要善于从所提供的数字或图形信息中寻找其共同之处，蕴含着“特殊——一般——特殊”的常用模式，体现了总结归纳的数学思想. 【经典专题突破】例1. 猜数字游戏中，小明写出如下一组数：2481632,,,,,57111935--，小亮猜想出第六个数字是6467-，根据此规律，第n 个数是 ．例2. （1）将一些形状相同的小五角星如下图所示的规律摆放，据此规律，第10个图形有 个五 角星.（2）下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有1颗棋子， 第②个图形一共有6颗棋子，第③个图形一共有16颗棋子，…，则第⑥个图形中棋子 的颗数为（ ）A.51B.70C.76D.81 例3. 如图，在一单位为1的方格纸上，123A A A ∆，345A A A ∆， 567A A A ∆，…，都是斜边在x 轴上、斜边长分别为 2,4,6,…的等腰直角三角形．若123A A A ∆的顶点坐标 分别为 1A (2,0)，2A (1,1)-，3A (0,0)，则依图中所示规律，2012A 的坐标为 ． 【仿真题型演练】 1. 观察下列一组数：32，54，76，98，1110，…… ，它们是按一定规律排列的，那么这一组数的第10个数是 ．2. 给定一列按规律排列的数： ,174,103,52,21，则这列数的第6个数是（ ）A ．376 B ．356 C ．315 D ．3973. 如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，…，依此规律，第11个图案需（ ）根火柴．A ．156B ．157C ．158D ．1594. 在下图中，每个图案均由边长为1的小正方形按一 定的规律堆叠而成，照此规律，第10个图案中共有 个小正方形.5. 如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第8个图形需要黑色棋子的个数是（ ）A ．48B ．80C ．90D ．866. 用火柴棒按下图中的方式搭图形，按照这种方式摆，第10个图形需要 根火柴棒．7. 如图，是一组按照某种规律摆放成的图案，则图5中三角形的个数是（ ）A ．8B ．9C ．16D ．178. 如图，在平面直角坐标系中，有若干个横坐标分别为整数的点， 其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1）， （1，2），（2，2）…根据这个规律，第2012个点的横坐标为 ．【一线名师预测】1. 将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，…，依次规律，第10个图形圆的个数为（ ）A ．114B. 104C. 85D. 762. 如图，用火柴棍摆出一列正方形图案，第①个图案用 火柴棍4根，第②个图案用火柴棍12根，第③个图 案用火柴棍24根，按这种方式摆下去，摆出第⑥个图 案用火柴棍的根数为（ ）A ．84B ．81C ．78D ．76第2题图①②③第8题图第1题图第7题图。

2020希望数学国际精英挑战营巅峰对决七年级个人战第一部分：90秒一题，共10题 1. 在实数99，23，0，12−，64325，π，79中，共有_______个无理数．2. 已知201920200a b −++=，则22a b a b−+的值为________．3. 如图，∠1= 150°，∠2 = 130°，∠3 = 70°，那么∠4 = ________度．4. 若m < 0，则点P ( 1 – m ，– |m | )在平面直角坐标系中的位置是（ ）．A ．第一象限B ．第二象限C ．第三象限D ．第四象限E ．坐标轴上5. 已知a ，b 互为倒数，c ，d 互为相反数，p 的绝对值为3，m 是数轴上表示原点的数，则220203c d p ab m ab p m+++++=_________．6.一个大长方形被分成四个小长方形，其中三个小长方形的面积已经标注在图中，那么阴影三角形的面积是_______．7.下列五个数中，不能写成50个连续自然数之和的是（）．A．16275 B．57825 C．55575 D．77755 E．576258.下列结论正确的是（）．A．若a < b，c < d，则ac < bdB．若a < b，c < d，且ab ≠ 0，则c d a b <C．若a < b，c < d，则a + c <b + dD．若a < b，c < d，则a –c < b –dE．若a < b，c < d，则a c< b d9.用“Θ”定义一种新运算：对于不相等的两个有理数a和b，20192020a ba ba b−Θ=−．如果xΘ4=2018，那么x=_______．10. 三视图如下图所示的几何体是（ ）．A B C D E第二部分：180秒一题，共15题 11. “?”=________．12. 计算：(–125)3× (64)2=（ ）．A ．–8×108B ．–8×109C ．–8×1010D ．8×109E ．–1×101013. 汤姆和杰瑞在环形跑道上跑步，速度保持恒定．汤姆12分钟跑5圈，杰瑞10分钟跑3圈．如果他们同时从起跑线出发，当他们再次同时经过起跑线时，两人一共跑了_______圈．14. 两个正整数的差是9，积是400，这两个正整数的和是_______．15. 如图，蚂蚁从A 点出发，沿正方体棱上的箭头方向爬行，最终到达F 点，有_______条不同的路线．16. 如果a ，b ，c ，d 是四个任意整数，那么2a b −，2b c −，2c d −，2d a−这四个数( )． A ．一定都不是整数 B ．至少有两个是整数 C ．至少有三个是整数 D ．可能都是正数 E ．可能都不是整数 17. 如果120192019m m a +=−，2120192019m m b ++=−，那么ba=_______．18. 下图是由一些完全相同的小正方体所搭的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，则这个几何体的主视图为（ ）．A B CD E19. 质数p ，q 满足5p + 7q = 126，则=_______．20. 图（1）中有1个圆，图（2）中有5个圆，图（3）中有21个圆，……照这样的规律排列下去，图（5）中有_______个圆．3p q−21.奶奶有两个孙女，奶奶的年龄是一个两位数，组成这个两位数的两个数字恰好是两个孙女的年龄．小孙女的年龄是5岁，三人的年龄和是69岁，奶奶_______岁．22.某毕业班56人照相，要求每一排比前一排多1人，不能只站1排，这样最前面一排应该站_______人．23.2000个正整数的和是2020，那么这2000个数中至多有_______个相同的数．24.有一列数：1，4，7，10，13，……，2017，2020，在每个数前面添加“+”或“–”号，然后把所有数相加，如果计算结果是非负数，那么这个非负数最小是_______．25.已知|1||2|3|1||2|7x xy y−++≤⎧⎨++−≤⎩，那么x–y的最大值为_______．答案题目 1 2 3 4 5 6 7 8 9 10 答案 4 4039 90 D 10 100 D C 8 A 题目11 12 13 14 15 16 17 18 19 20 答案30 B 43 41 6 E 2019 E 330 341 题目21 22 23 24 25答案57 5 1999 1 4。

巅峰对决七年级下册数学单元检测1、3．(2020·新高考Ⅰ，1,5分)设集合A={x|1≤x≤3}，B={x|2<x<4}，则A∪B=( ) [单选题] * A．{x|2<x≤3}B．{x|2≤x≤3}C．{x|1≤x<4}(正确答案)D．{x|1<x<4}2、2.比3大- 1的数是[单选题] *A.2(正确答案)B.4C. - 3D. - 23、计算的结果是( ) [单选题] *A. -p2?(正确答案)B. p2?C. -p1?D. p1?4、2．(2020·新高考Ⅱ，1,5分)设集合A={2,3,5,7}，B={1,2,3,5,8}，则A∩B=( ) [单选题] * A．{1,8}B．{2,5}C．{2,3,5}(正确答案)D．{1,2,3,5,7,8}5、260°是第（）象限角？[单选题] *第一象限第二象限第三象限(正确答案)第四象限6、下列函数中奇函数是（）[单选题] *A、y=2sin x(正确答案)B、y=3sin xC、y=2D、y=7、14．数﹣在数轴上的位置可以是（）[单选题] *A．点A与点B之间(正确答案)B．点B与点O之间C．点O与点D之间D．点D与点E之间8、下列函数是奇函数的是（）[单选题] *A、f（x）=3x(正确答案)B、f（x）=4xC、f（x）= +2x-1D、f（x）=9、32、在、、、、、3.14这六个数中, 无理数的个数有（）[单选题] *A) 1 个;B) 2 个; (正确答案)C) 3 个;D) 4 个.10、6.若x是- 3的相反数，|y| = 5，则x + y的值为（）[单选题] *A.2B.8C. - 8或2D.8或- 2(正确答案)11、9．如果向东走记为，则向西走可记为() [单选题] *A+3mB+2mC-3m(正确答案)D-2m12、29．已知2a＝5，2b＝10，2c＝50，那么a、b、c之间满足的等量关系是（）[单选题] *A．ab＝cB．a+b＝c(正确答案)C．a：b：c＝1：2：10D．a2b2＝c213、46、在直角三角形ABC中，，，则的三条高之和为（）[单选题] *A．8.4B．9.4(正确答案)C．10.4D．11.14、20．水文观测中，常遇到水位上升或下降的问题．我们规定：水位上升为正，水位下降为负；几天后为正，几天前为负．如果水位每天上升3cm，今天的水位为0cm，那么2天前的水位用算式表示正确的是（）[单选题] *A．（+3）×（+2）B．（+3）×（﹣2）(正确答案)C．（﹣3）×（+2）D．（﹣3）×（﹣2）15、14．在防治新型冠状病毒的例行体温检查中，检查人员将高出37℃的部分记作正数，将低于37℃的部分记作负数，体温正好是37℃时记作“0”。