第3章 控制系统的数学模型与转换
- 格式:ppt
- 大小:3.11 MB
- 文档页数:2

第二章自动控制系统的数学模型教学目的:(1)建立动态模拟的概念,能编写系统的微分方程。
(2)掌握传递函数的概念及求法。
(3)通过本课学习掌握电路或系统动态结构图的求法,并能应用各环节的传递函数,求系统的动态结构图。
(4)通过本课学习掌握电路或自动控制系统动态结构图的求法,并对系统结构图进行变换。
(5)掌握信号流图的概念,会用梅逊公式求系统闭环传递函数。
(6)通过本次课学习,使学生加深对以前所学的知识的理解,培养学生分析问题的能力教学要求:(1)正确理解数学模型的特点;(2)了解动态微分方程建立的一般步骤和方法;(3)牢固掌握传递函数的定义和性质,掌握典型环节及传递函数;(4)掌握系统结构图的建立、等效变换及其系统开环、闭环传递函数的求取,并对重要的传递函数如:控制输入下的闭环传递函数、扰动输入下的闭环传递函数、误差传递函数,能够熟练的掌握;(5)掌握运用梅逊公式求闭环传递函数的方法;(6)掌握结构图和信号流图的定义和组成方法,熟练掌握等效变换代数法则,简化图形结构,掌握从其它不同形式的数学模型求取系统传递函数的方法。
教学重点:有源网络和无源网络微分方程的编写;有源网络和无源网络求传递函数;传递函数的概念及求法;由各环节的传递函数,求系统的动态结构图;由各环节的传递函数对系统的动态结构图进行变换;梅逊增益公式的应用。
教学难点:举典型例题说明微分方程建立的方法;求高阶系统响应;求复杂系统的动态结构图;对复杂系统的动态结构图进行变换;求第K条前向通道特记式。
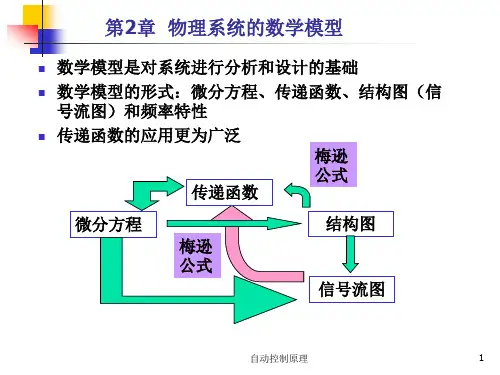
的余子式k教学方法:讲授本章学时:10学时主要内容:2.0 引言2.1 动态微分方程的建立2.2 线性系统的传递函数2.3 典型环节及其传递函数2.4系统的结构图2.5 信号流图及梅逊公式2.0引言:什么是数学模型?为什么要建立系统的数学模型?1. 系统的数学模型:描述系统输入输出变量以及各变量之间关系的数学表达式。
1) 动态模型:描述系统处于暂态过程中个变量之间关系的表达式,他一般是时间函数。



可编辑修改精选全文完整版控制系统的数学模型及传递函数2-1 拉普拉斯变换的数学方法拉氏变换是控制工程中的一个基本数学方法,其优点是能将时间函数的导数经拉氏变换后,变成复变量S的乘积,将时间表示的微分方程,变成以S表示的代数方程。
一、拉氏变换与拉氏及变换的定义1、拉氏变换:设有时间函数,其中,则f(t)的拉氏变换记作:称L—拉氏变换符号;s-复变量; F(s)—为f(t)的拉氏变换函数,称为象函数。
f(t)—原函数拉氏变换存在,f(t)必须满足两个条件(狄里赫利条件):1)在任何一有限区间内,f(t)分断连续,只有有限个间断点。
2)当时,,M,a为实常数。
2、拉氏反变换:将象函数F(s)变换成与之相对应的原函数f(t)的过程。
—拉氏反变换符号关于拉氏及变换的计算方法,常用的有:①查拉氏变换表;②部分分式展开法。
二、典型时间函数的拉氏变换在实际中,对系统进行分析所需的输入信号常可化简成一个成几个简单的信号,这些信号可用一些典型时间函数来表示,本节要介绍一些典型函数的拉氏变换。
1.单位阶跃函数2.单位脉冲函数3.单位斜坡函数4.指数函数5.正弦函数sinwt由欧拉公式:所以,6.余弦函数coswt其它的可见表2-1:拉氏变换对照表F(s) f(t)11(t)t三、拉氏变换的性质1、线性性质若有常数k1,k2,函数f1(t),f2(t),且f1(t),f2(t)的拉氏变换为F1(s),F2(s),则有:,此式可由定义证明。
2、位移定理(1)实数域的位移定理若f(t)的拉氏变换为F(s),则对任一正实数a有, 其中,当t<0时,f(t)=0,f(t-a)表f(t)延迟时间a. 证明:,令t-a=τ,则有上式=例:, 求其拉氏变换(2)复数域的位移定理若f(t)的拉氏变换为F(s),对于任一常数a,有证:例:求的拉氏变换3、微分定理设f(t)的拉氏变换为F(s),则其中f(0+)由正向使的f(t)值。






第三章 控制系统数学模型及其转换3.1 控制系统常用数学模型(线性时不变\ LTI 模型) ● 传递函数模型● 零极点增益模型● 状态空间模型● 部分分式模型1.传递函数模型(transfer function model )连续系统传递函数为:n n n m m m a s a s a b s b s b s G ++++++=-- 110110)(离散系统传递函数为:n n n m m m a z a z a b z b z b z G ++++++=-- 110110)(MATLAB 中可采用tf 函数建立传递函数,其调用格式为:(设num=[b 0,b 1,…,b m ]为分子多项式系数组成的向量,den=[a0,a1,…,a m]为分母多项式系数组成的向量)①sys=tf(num,den)生成连续传递函数。
②sys=tf(num,den,T s)生成离散传递函数,T s为采样时间。
当T s=[ ]或T s=-1时,表示采样时刻未指定。
③sys=tf(num,den,’Property1’,Value1,’Property2’ , Value2,…, ’PropertyN’,ValueN)生成具有LTI模型属性的连续传递函数。
④sys=tf(num,den,T s ,’Property1’,Value1,’Property2’ , Value2,…, ’PropertyN’,ValueN)生成具有LTI模型属性的离散传递函数。
⑤sys=tf(‘s’)用于生成s域的有理传递函数⑥sys=tf(‘z’, T s)用于生成z域的有理传递函数,且采样周期为T s ⑦sys_tf=tf(sys)将其它模型转换成传递函数的形式(s→s,z→z) 例:给定SISO系统的传递函数为:132106126)(23423+++++++=s s s s s s s s G用MATLAB 语句表示该传递函数。
解:法1: num=[6,12,6,10];den=[1,2,3,1,1];sys=tf(num,den)结果为:Transfer function:6 s^3 + 12 s^2 + 6 s + 10----------------------------------s^4 + 2 s^3 + 3 s^2 + s + 1法2:s=tf('s');sys=(6*s^3+12*s^2+6*s+10)/(s^4+2*s^3+3*s^2+s+1) 结果仍为:Transfer function:6 s^3 + 12 s^2 + 6 s + 10----------------------------------s^4 + 2 s^3 + 3 s^2 + s + 1也可采用printsys 函数,如:num=[6,12,6,10];den=[1,2,3,1,1];printsys (num,den) % printsys(num,den,’s ’)printsys(num,den,’z ’), 默认时为S 域。
实验一 控制系统模型的建立与转换一、实验目的与要求1、掌握Matlab 中连续系统、离散系统各种数学模型的建立方法;2、掌握Matlab 中各种数学模型之间的转换;3、熟悉Matlab 中控制框图的化简;二、实验类型设计三、实验原理及说明1.控制系统的数学模型及其意义用来描述系统因果关系的数学表达式称为系统的数学模型。
控制系统数学模型有多种形式。
时域中常用的有微分方程、差分方程;频域中常用的有传递函数、方框图和频率特性。
2.建立控制系统数学模型的不同方法 (1)线性系统的传递函数模型:11211121...()()()...m m n m n n n n b s b s b s b C s G s R s a s a s a s a -+-+++++==++++传递函数建立的MA TLAB 相关函数(2)控制系统零极点函数模型:1212()()...()()()()...()m n s z s z s z G s Ks p sp s p ---=---零极点模型建立的MATLAB 相关函数3.控制系统的不同模型表示及其转换在线性系统理论中,一般常用的数学模型形式有传递函数模型和零极点增益模型。
这些模型之间都有着内在的联系,可以相互进行转换。
(1)把其它类型的模型转换为函数表示的模型(2)将本类型模型参数转换为其它类型模型参数4. 方框图模型的连接化简 (1)串联连接的化简(2)并联连接的化简(3)反馈连接的化简(a )正反馈连接(b )负反馈连接(4)方框图的其它变换化简(a )相加点后移等效变换(b )相加点前移等效变换(c )分支点后移等效变换(d )分支点前移等效变换(5)系统模型连接化简函数 四、实验仪器五、实验内容和步骤( k=N%3+1,N 为学号末位数)1、连续线性系统的数学模型建立及转换611623)(G 232+++++=s s s s s s① 请用合适的格式,将上面的传递函数模型输入MA TLAB 环境; ② 将模型转换成零极点形式、画出零极点位置;③ 采样周期为Ts=0.5ks 时,将上面的连续系统转换为离散系统; ④ 若上面模型中,时间延迟常数为0.78k ,如何建立该传函模型? 2、离散线性系统的数学模型建立及转换① 请用合适的格式,将下面的传递函数模型输入MA TLAB 环境;()s T z z z z z H k 1.0 ,)99.02.0)(k (568.022=+--+=② 将模型转换成零极点形式、画出零极点位置;3、已知系统的方框图如图所示,试推导出从输入信号r(t) 到输出信号y(t) 的总系统模型。