高三数学一轮复习 简单几何体的表面积与体积随堂检测 文 北师大版

课时规范练34 基本立体图形及空间几何体的表面积和体积基础巩固组1.能旋转形成如图所示的几何体的平面图形是( )答案:A解析:此几何体自上向下是由一个圆锥、两个圆台和一个圆柱构成,是由A 中的平面图形旋转形成的.故选A .2.(2022·广东潮州二模)已知一个圆柱的轴截面为正方形,且它的侧面积为36π,则该圆柱的体积为( ) A.16π B.27πC.36πD.54π答案:D解析:设圆柱底面半径为R ,高为h ,则{ℎ=2R ,2πRℎ=36π,解得{R =3,ℎ=6,∴圆柱的体积V=πR 2h=54π.3.(2022·广东深圳二模)已知一个球的表面积在数值上是它的体积的√3倍,则这个球的半径是( ) A.2 B.√2C.3D.√3答案:D解析:设球的半径为R ,则根据球的表面积公式和体积公式,可得4πR 2=43πR 3×√3,化简得R=√3. 4.(2023·福建福州格致中学模拟)已知一个直三棱柱的高为2,其底面ABC 水平放置的直观图为A'B'C',如图所示,其中O'A'=O'B'=O'C'=1,则此三棱柱的表面积为( )A.4+4√2B.8+4√2C.8+4√5D.8+8√5答案:C解析:由斜二测画法可得底面的平面图如图所示,其中OA=2OB=2OC=2,所以AB=AC=√5,所以此三棱柱的表面积S=2×12×2×2+(2+2√5)×2=8+4√5.5.(2022·山东菏泽一模)如图1,在高为h的直三棱柱容器ABC-A1B1C1中,AB=AC=2,AB⊥AC.现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为A1B1C(如图2),则容器的高h为()图1图2A.3B.4C.4√2D.6答案:A解析:在图1中V水=12×2×2×2=4,在图2中,V水=V ABC-A1B1C1−V C-A1B1C1=12×2×2×h-13×1 2×2×2×h=43h,∴43h=4,∴h=3.6.(2022·广东佛山二模)如图,某几何体由共底面的圆锥和圆柱组合而成,且圆柱的两个底面圆周和圆锥的顶点均在体积为36π的球的球面上,若圆柱的高为2,则圆锥的侧面积为()A.2√6πB.4√6πC.16πD.16π3答案:B解析:依题意,作球的剖面图,其中,O 是球心,E 是圆锥的顶点,EC 是圆锥的母线.设球的半径为R ,则43πR 3=36π,R=3.∵圆柱的高为2,∴OD=1,DE=3-1=2,DC=√32-12=2√2,母线EC=√22+8=2√3.∴圆锥的侧面积S=12·EC ·2π·DC=12×2√3×2π×2√2=4√6π.故选B .7.(2022·全国甲,理9)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若S 甲S 乙=2,则V 甲V 乙=( )A.√5B.2√2C.√10D.5√104答案:C如图,甲、乙两个圆锥的侧面展开图刚好拼成一个圆,设圆的半径(即圆锥的母线长)为3,则圆的周长为6π,甲、乙两个圆锥的底面半径分别为r 1,r 2,高分别为h 1,h 2,则2πr 1=4π,2πr 2=2π,则r 1=2,r 2=1,由勾股定理得,h 1=√5,h 2=2√2,所以V 甲V 乙=13πr 12ℎ113πr 22ℎ2=2√512×2√2=√10.故选C .8.(多选)(2023·广东广州高三检测)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台O 1O 2,在轴截面ABCD 中,AB=AD=BC=2 cm,且CD=2AB ,则( )A.该圆台的高为1 cmB.该圆台轴截面面积为3√3 cm 2C.该圆台的体积为7√3π3cm 3 D.一只小虫从点C 沿着该圆台的侧面爬行到AD 的中点,所经过的最短路程为5 cm 答案:BCD解析:如图,作BE ⊥CD 交CD 于点E ,易得CE=CD -AB2=1,则BE=√22-12=√3,则圆台的高为√3cm,故A 错误;圆台的轴截面面积为12×(2+4)×√3=3√3(cm 2),故B 正确;圆台的体积为13×√3×(π+4π+√π·4π)=7√3π3(cm 3),故C 正确;由圆台补成圆锥,可得大圆锥的母线长为4cm,底面半径为2cm,侧面展开图的圆心角θ=2π·24=π,设P 为AD 的中点,连接CP ,可得∠COD=π2,OC=4,OP=3,则CP=√42+32=5,从点C 沿着该圆台的侧面爬行到AD 的中点,所经过的最短路程为5cm,故D 正确.故选BCD .9.(2023·湖南长沙一中高三检测)在棱长为2的正方体ABCD-A 1B 1C 1D 1中,E ,F ,G ,H 分别为棱AB ,BC ,CD ,DA 的中点,将该正方体挖去两个四分之一圆锥,得到如图所示的几何体,则该几何体的体积为 .答案:8-π3解析:∵该几何体为正方体挖去两个四分之一圆锥,圆锥底面圆半径R=1,高h=2,∴该几何体的体积V=23-12×13×π×12×2=8-π3.10.(2022·福建漳州一模)某中学开展劳动实习,学习加工制作包装盒.现将一张足够用的正方形硬纸片加工制作成轴截面的顶角为60°,高为6的圆锥形包装盒,若在该包装盒中放入一个球形冰淇淋(内切),则该球形冰淇淋的表面积为 . 答案:16π解析:如图,由题意知,∠BAC=60°,AO 1=6,故在Rt △AO 1C 中,AC=4√3,O 1C=2√3.设内切球球心为O ,半径为R ,则OD=OO 1=R.在Rt △ADO 中,∠OAD=30°,所以2R=6-R ,解得R=2.所以该球形冰淇淋的表面积S=4πR 2=16π.综合提升组11.(2022·山东青岛二模)《九章算术》中记录的“羡除”是算学和建筑学术语,指的是一段类似隧道形状的几何体.如图,羡除ABCDEF 中,底面ABCD 是正方形,EF ∥平面ABCD ,EF=2,其余棱长都为1,则这个几何体的外接球的体积为( )A.√2π3B.4π3C.8√2π3D.4π答案:B解析:连接AC ,BD 交于点M ,取EF 的中点O ,连接OM ,则OM ⊥平面ABCD ,取BC 的中点G ,连接FG ,作GH ⊥EF ,垂足为H ,如图所示.由题意可知,HF=12,FG=√32,所以HG=√FG 2-HF 2=√22,所以OM=HG=√22.又AM=√22,所以OA=√OM 2+AM 2=1.又OE=1,所以OA=OB=OC=OD=OE=OF=1,即这个几何体的外接球的球心为O ,半径为1,所以这个几何体的外接球的体积为V=43×π×13=43π.12.(2022·山东泰安三模)如图,已知三棱柱ABC-A 1B 1C 1的底面是等腰直角三角形,AA 1⊥底面ABC ,AC=BC=2,AA 1=4,点D 在上底面A 1B 1C 1(包括边界)上运动,则三棱锥D-ABC 的外接球表面积的最大值为( )A.81π4B.24πC.243π16D.8√6π答案:B解析:因为△ABC 为等腰直角三角形,AC=BC=2,所以△ABC 的外接圆的圆心为AB 的中点O 1,且AO 1=√2.连接O 1与A 1B 1的中点E ,则O 1E ∥AA 1,所以O 1E ⊥平面ABC.设球的球心为O ,由球的截面性质可得O 在O 1E 上,设OO 1=x ,DE=t (0≤t ≤√2),球的半径为R.因为OA=OD=R ,所以√2+x 2=√(4-x)2+t2,所以t2=8x-14.又0≤t≤√2,所以74≤x≤2.因为R2=2+x2,所以8116≤R2≤6,所以三棱锥D-ABC的外接球表面积的最大值为24π.13.(多选)(2022·山东滨州二模)在边长为4的正方形ABCD中,如图1所示,E,F,M分别为BC,CD,BE的中点,分别沿AE,AF及EF所在直线把△AEB,△AFD和△EFC折起,使B,C,D三点重合于点P,得到三棱锥P-AEF,如图2所示,则下列结论正确的是()图1图2A.PA⊥EFB.三棱锥M-AEF的体积为4C.三棱锥P-AEF外接球的表面积为24πD.过点M的平面截三棱锥P-AEF的外接球所得截面的面积的取值范围为[π,6π]答案:ACD解析:由题意,将三棱锥补形为长方体,其中PA=4,PE=2,PF=2,如图所示.对于A,因为AP⊥PE,AP ⊥PF,PE∩PF=P,PE,PF⊂平面PEF,所以AP⊥平面PEF,又EF⊂平面PEF,所以PA⊥EF,故A正确;对于B,因为M为PE的中点,所以V M-AEF=12V P-AEF=12V A-PEF=12×13×12×2×2×4=43,故B错误;对于C,三棱锥P-AEF的外接球即为补形后长方体的外接球,所以外接球的直径2R=√22+22+42=2√6,所以三棱锥P-AEF外接球的表面积为S=4πR2=24π,故C正确;对于D,过点M的平面截三棱锥P-AEF的外接球所得截面为圆,其中最大截面为过球心O的大圆,此时截面圆的面积为πR2=π(√6)2=6π,最小截面为过点M且垂直于球心O与M连线的圆,此时截面圆半径r=√R 2-OM 2=√6-5=1,截面圆的面积为πr 2=π,所以过点M 的平面截三棱锥P-AEF 的外接球所得截面的面积的取值范围为[π,6π],故D 正确.故选ACD .14.十字贯穿体(如图1)是美术素描学习中一种常见的教具.如图2,该十字贯穿体由两个全等的正四棱柱组合而成,且两个四棱柱的侧棱互相垂直,若底面正方形边长为2,则这两个正四棱柱公共部分所构成的几何体的内切球的体积为 .图1图2答案:4π3解析:该几何体的直观图如图所示,这两个正四棱柱公共部分所构成的几何体为两个全等的四棱锥S-ABCD 和P-ABCD.设内切球的半径为R ,AC 的中点为H ,由题意,H 为内切球的球心,连接BH ,SH ,可知SH 即为四棱锥S-ABCD 的高,在Rt △ABH 中,BH=√AB 2-AH 2=√6-2=2.又AC=SB=2√2,∴S 四边形ABCD =12×2√2×2×2=4√2.又BH=SH ,∴V S-ABCD =13SH ·S 四边形ABCD =13×2×4√2=8√23.由八个侧面的面积均为2√2,∴13R ×2√2×8=2×8√23,得R=1.故几何体的内切球的体积为4π3.创新应用组15.如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为120°,腰为3的等腰三角形,则该几何体的体积为( )A.23B.24C.26D.27答案:D解析:该几何体由直三棱柱AFD-BHC 及直三棱柱DGC-AEB 组成,作HM ⊥CB 于M ,如图.因为CH=BH=3,∠CHB=120°,所以CM=BM=3√32,HM=32.因为重叠后的底面为正方形,所以AB=BC=3√3.在直棱柱AFD-BHC 中,AB ⊥平面BHC ,则AB ⊥HM.由AB ∩BC=B ,可得HM ⊥平面ADCB.设重叠后的EG 与FH 的交点为I,则V I -BCDA =13×3√3×3√3×32=272,V AFD-BHC =12×3√3×32×3√3=814,则该几何体的体积V=2V AFD-BHC -V I -BCDA =2×814−272=27.。

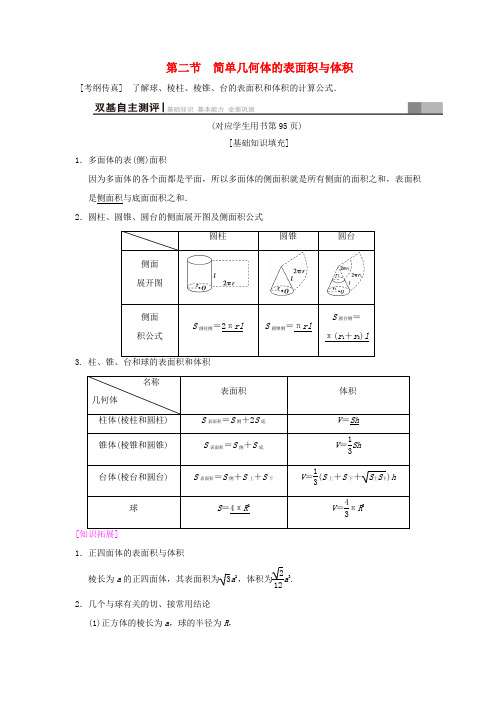
第二节 简单几何体的表面积与体积[考纲传真] 了解球、棱柱、棱锥、台的表面积和体积的计算公式．(对应学生用书第95页)[基础知识填充]1．多面体的表(侧)面积因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．2．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱 圆锥 圆台侧面 展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r 1＋r 2)l3. 名称几何体 表面积体积柱体(棱柱和圆柱) S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥)S 表面积＝S 侧＋S 底 V ＝13Sh台体(棱台和圆台)S 表面积＝S 侧＋S 上＋S 下V ＝13(S 上＋S 下＋S 上S 下)h球S ＝4πR 2V ＝43πR 3[1．正四面体的表面积与体积棱长为a 的正四面体，其表面积为3a 2，体积为212a 3. 2．几个与球有关的切、接常用结论 (1)正方体的棱长为a ，球的半径为R ，①若球为正方体的外接球，则2R ＝3a ； ②若球为正方体的内切球，则2R ＝A ． ③若球与正方体的各棱相切，则2R ＝2A ．(2)若长方体的同一顶点的三条棱长分别为a ，b ，c ，外接球的半径为R ，则2R ＝a 2＋b 2＋c 2.(3)正四面体的外接球与内切球的半径之比为3∶1，棱长为a 的正四面体，其内切球半径R 内＝612a ，外接球半径R 外＝64A ． [基本能力自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)锥体的体积等于底面面积与高之积．( ) (2)球的体积之比等于半径比的平方．( ) (3)台体的体积可转化为两个锥体的体积之差．( ) (4)已知球O 的半径为R ，其内接正方体的边长为a ，则R ＝32A ．( ) [答案] (1)× (2)× (3)√ (4)√2．(教材改编)已知圆锥的表面积等于12π cm 2，其侧面展开图是一个半圆，则底面圆的半径为( ) A ．1 cm B ．2 cm C ．3 cmD ．32cm B [S 表＝πr 2＋πrl ＝πr 2＋πr ·2r ＝3πr 2＝12π，∴r 2＝4， ∴r ＝2(cm)．]3．(2015·全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图7­2­1，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )图7­2­1A ．14斛B ．22斛C ．36斛D ．66斛B [设米堆的底面半径为r 尺，则π2r ＝8，所以r ＝16π，所以米堆的体积为V ＝14×13π·r 2·5＝π12×⎝ ⎛⎭⎪⎫16π2×5≈3209(立方尺)．故堆放的米约有3209÷1.62≈22(斛)．故选B ．]4．(2017·全国卷Ⅱ)长方体的长、宽、高分别为3,2,1，其顶点都在球O 的球面上，则球O 的表面积为________．14π [∵长方体的顶点都在球O 的球面上， ∴长方体的体对角线的长度就是其外接球的直径． 设球的半径为R ， 则2R ＝32＋22＋12＝14. ∴球O 的表面积为S ＝4πR 2＝4π×⎝⎛⎭⎪⎫1422＝14π.] 5．(2017·郑州质检)某几何体的三视图如图7­2­2所示(单位：cm)，则该几何体的体积是________cm 3.【导学号：00090233】图7­2­2323[由三视图可知该几何体是由棱长为2 cm 的正方体与底面为边长为2 cm 的正方形、高为2 cm 的四棱锥组成，V ＝V 正方体＋V 四棱锥＝8 cm 3＋83 cm 3＝323cm 3.](对应学生用书第96页)简单几何体的表面积(1)某几何体的三视图如图7­2­3所示，则该几何体的表面积等于( )图7­2­3A ．8＋2 2B ．11＋2 2C ．14＋2 2D ．15(2)(2018·江西七校联考)若某空间几何体的三视图如图7­2­4所示，则该几何体的表面积是( )【导学号：00090234】图7­2­4A ．48＋πB ．48－πC ．48＋2πD ．48－2π(1)B (2)A [(1)由三视图知，该几何体是一个直四棱柱，上、下底面为直角梯形，如图所示．直角梯形斜腰长为12＋12＝2，所以底面周长为4＋2，侧面积为4＋22＋2＋2＝8＋22，两底面的面积和为2×12×1×(1＋2)＝3.所以该几何体的表面积为8＋22＋3＝11＋2 2.(2)该几何体是正四棱柱挖去了一个半球，正四棱柱的底面是正方形(边长为2)，高为5，半球的半径是1，那么该几何体的表面积为S ＝2×2×2＋2×4×5－π×12＋2π×12＝48＋π，故选A ．[规律方法] 1.(1)多面体与旋转体的表面积等于侧面面积与底面面积之和．(2)简单组合体：应搞清各构成部分，并注意重合部分的处理．2．若以三视图的形式给出，解题的关键是对给出的三视图进行分析，从中发现几何体中各元素间的位置关系及数量关系，得到几何体的直观图，然后根据条件求解．[变式训练1] (1)(2016·全国卷Ⅲ)如图7­2­5，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为( )图7­2­5A ．18＋36 5B ．54＋18 5C ．90D ．81(2)(2016·全国卷Ⅰ)如图7­2­6，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是( )图7­2­6A ．17πB ．18πC ．20πD ．28π(1)B (2)A [(1)由三视图可知该几何体是底面为正方形的斜四棱柱，其中有两个侧面为矩形，另两个侧面为平行四边形，则表面积为(3×3＋3×6＋3×35)×2＝54＋18 5.故选B ．(2)由几何体的三视图可知，该几何体是一个球体去掉上半球的14，得到的几何体如图．设球的半径为R ，则43πR 3－18×43πR 3＝283π，解得R ＝2.因此它的表面积为78×4πR 2＋34πR2＝17π.故选A ．]简单几何体的体积(1)在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A ．2π3B ．4π3C ．5π3D ．2π(2)(2017·全国卷Ⅱ)如图7­2­7，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )图7­2­7A ．90πB ．63πC ．42πD ．36π(1)C (2)B [(1)过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥而得到的，如图所示．由于V 圆柱＝π·AB 2·BC ＝π×12×2＝2π，V 圆锥＝13π·CE 2·DE ＝13π·12×(2－1)＝π3，所以该几何体的体积V ＝V 圆柱－V 圆锥＝2π－π3＝5π3.(2)法一：(割补法)如图所示，由几何体的三视图，可知该几何体是一个圆柱被截去上面虚线部分所得．将圆柱补全，并将圆柱体从点A 处水平分成上下两部分．由图可知，该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的12，所以该几何体的体积V ＝π×32×4＋π×32×6×12＝63π.故选B ．法二：(估值法)由题意，知12V圆柱＜V 几何体＜V圆柱．又V圆柱＝π×32×10＝90π，∴45π＜V几何体＜90π.观察选项可知只有63π符合．故选B ．][规律方法] 1.若所给定的几何体是柱体、锥体或台体，则可直接利用公式进行求解． 2．若所给定的几何体的体积不能直接利用公式得出，则常用转换法(转换的原则是使底面面积和高易求)、分割法、补形法等方法进行求解．3．若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．[变式训练2] (1)(2018·唐山模拟)一个几何体的三视图如图7­2­8所示，则其体积为( )图7­2­8A ．π＋2B ．2π＋4C ．π＋4D ．2π＋2(2)(2016·天津高考)已知一个四棱锥的底面是平行四边形，该四棱锥的三视图如图7­2­9所示(单位：m)，则该四棱锥的体积为________m 3.【导学号：00090235】图7­2­9(1)A (2)2 [(1)该几何体为组合体，左边为三棱柱，右边为半圆柱，其体积V ＝12×2×1×2＋12π×12×2＝2＋π.故选A ．(2)由三视图知，四棱锥的高为3，底面平行四边形的一边长为2，对应高为1，所以其体积V ＝13Sh ＝13×2×1×3＝2.]多面体与球的切、接问题(2016·全国卷Ⅲ)在封闭的直三棱柱ABC ­A 1B 1C 1内有一个体积为V 的球．若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A ．4πB ．9π2C ．6πD ．32π3B [由AB ⊥BC ，AB ＝6，BC ＝8，得AC ＝10，要使球的体积V 最大，则球与直三棱柱的部分面相切，若球与三个侧面相切，设底面△ABC 的内切圆的半径为r .则12×6×8＝12×(6＋8＋10)·r ，则r ＝2. 此时2r ＝4＞3，不合题意．因此球与三棱柱的上、下底面相切时，球的半径R 最大．由2R ＝3，即R ＝32.故球的最大体积V ＝43πR 3＝92π.][母题探究1] 若本例中的条件变为“直三棱柱ABC ­A 1B 1C 1的6个顶点都在球O 的球面上”，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，求球O 的表面积． [解] 将直三棱柱补形为长方体ABEC ­A 1B 1E 1C 1， 则球O 是长方体ABEC ­A 1B 1E 1C 1的外接球， 所以体对角线BC 1的长为球O 的直径． 因此2R ＝32＋42＋122＝13， 故S 球＝4πR 2＝169π.[母题探究2] 若本例中的条件变为“正四棱锥的顶点都在球O 的球面上”，若该棱锥的高为4，底面边长为2，求该球的体积． [解] 如图，设球心为O ，半径为r ，则在Rt △AFO 中，(4－r )2＋(2)2＝r 2，解得r ＝94，则球O 的体积V 球＝43πr 3＝43π×⎝ ⎛⎭⎪⎫943＝243π16.[规律方法] 1.与球有关的组合体问题，一种是内切，一种是外接．球与旋转体的组合通常是作它们的轴截面解题，球与多面体的组合，通过多面体的一条侧棱和球心，或“切点”“接点”作出截面图，把空间问题化归为平面问题．2．若球面上四点P ，A ，B ，C 中PA ，PB ，PC 两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正方体确定直径解决外接问题．[变式训练3] (1)(2015·全国卷Ⅱ)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O ­ABC 体积的最大值为36，则球O 的表面积为( ) A ．36π B ．64π C ．144πD ．256π(2)(2017·全国卷Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) 【导学号：00090236】 A ．πB ．3π4C ．π2D ．π4(1)C (2)B [(1)如图，设球的半径为R ，∵∠AOB ＝90°，∴S △AOB ＝12R 2.∵V O ­ABC ＝V C ­AOB ，而△AOB 面积为定值，∴当点C 到平面AOB 的距离最大时，V O ­ABC 最大，∴当C 为与球的大圆面AOB 垂直的直径的端点时，体积V O ­ABC 最大为13×12R 2×R ＝36，∴R ＝6，∴球O 的表面积为4πR 2＝4π×62＝144π. 故选C ．(2)设圆柱的底面半径为r ，球的半径为R ，且R ＝1，由圆柱两个底面的圆周在同一个球的球面上可知，r ，R 及圆柱的高的一半构成直角三角形． ∴r ＝1－⎝ ⎛⎭⎪⎫122＝32. ∴圆柱的体积为V ＝πr 2h ＝34π×1＝3π4.故选B ．]。

2011《金版新学案》高三数学一轮复习 简单几何体的表面积与体积随堂检测 理 北师大版(本栏目内容，学生用书中以活页形式单独装订成册！) 一、选择题(每小题6分，共36分)1．正棱锥的高缩小为原来的12，底面外接圆半径扩大为原来的3倍，则它的体积是原来体积的( )A.32倍B.92倍C.34倍D.94倍 【解析】 设原棱锥高为h ，底面面积为S ， 则V ＝13Sh ，新棱锥的高为12h ，底面面积为9S.∴V′＝13·9S·12h ＝13Sh·92，∴V′V ＝92. 【答案】 B2．如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积为( )A ．32πB ．16πC ．12πD ．8π【解析】 由三视图可知几何体是半径为2的半球，故其表面积应为半球的表面积与底面圆的面积之和，即S ＝2πR 2＋πR 2＝3πR 2＝12π.【答案】 C3．当圆锥的侧面积和底面积的比值是2时，圆锥轴截面的顶角等于( ) A ．45° B．60° C ．90° D．120°【解析】 设圆锥的母线长为l ，底面半径为r ， 则πrl πr 2＝2，∴lr＝2， 设轴截面顶角的一半为α，则sin α＝r l ＝22，∴α＝45°，2α＝90°.【答案】 C4．在三棱锥A —BCD 中，侧棱AB ，AC ，AD 两两垂直，△ABC，△ACD，△ADB 的面积分别为22，32，62，则该三棱锥的体积为( ) A. 6 B.66C ．6D ．2 6【解析】 12AB·AC＝22，12AD·AC＝32，12AB·AD＝62，∴AB＝2，AC ＝1，AD ＝ 3. ∴V＝13·12·1·2·3＝66.【答案】 B5．把由曲线y ＝|x|和y ＝2围成的图形绕x 轴旋转360°，所得旋转体的体积为( )A.8π3B.10π3C.6π3 D.32π3【解析】由题意，y=|x|和y=2围成图中阴影部分的图形，旋转体为一个圆柱挖去两个相同的共顶点的圆锥．【答案】 D6．不共面的三条定直线l1，l2，l3互相平行，点A在l1上，点B在l2上，C、D两点在l3上，若CD＝a(定值)，则三棱锥A－BCD的体积( )A．由A点的变化而变化B．由B点的变化而变化C．有最大值，无最小值D．为定值【解析】如图，把△BCD当作三棱锥的底面，AO⊥平面BCD于O，∵l2∥l3，∴B点在l2上什么位置，△BCD的面积不变．又∵l2∥l3，∴l2、l3确定一个平面α，∵l1∥l2，且点A不在l2、l3确定的平面α上，∴l1平行于l2、l3确定的平面α，从而不论A在l1的什么位置，高AO的长总不变．又V=×高×底面积，故无论A、B在什么位置时，其体积的值恒定．【答案】 D二、填空题(每小题6分，共18分)7. 如图，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是直径为1的圆，那么这个几何体的侧面积为 .【解析】 由三视图的知识，它是底面直径与高均为1的圆柱，所以侧面积S=π. 【答案】 π8．正三棱台高为12 cm ，上、下底面面积之比为1∶4，它的体积为28 cm 3，则下底面面积为________．【解析】 设下底面面积为S cm 2， 则上底面面积为14S cm 2，∴13⎝ ⎛⎭⎪⎫S ＋14S ＋S×14S ×12＝28， ∴S＝4. 【答案】 4 cm 29．(2009年全国卷Ⅰ)直三棱柱ABC －A 1B 1C 1的各顶点都在同一球面上．若AB ＝AC ＝AA 1＝2，∠BAC＝120°，则此球的表面积等于________．【解析】 在△ABC 中，由余弦定理知BC 2＝AB 2＋AC 2－2AB·AC·cos 120°＝4＋4－2×2×2×⎝ ⎛⎭⎪⎫－12＝12， ∴BC＝2 3.由正弦定理知△ABC 的外接圆半径r 满足23sin120°＝2r ，∴r＝2，由题意知球心到平面ABC 的距离为1，设球的半径为R ，则R ＝22＋1＝5， ∴S 球＝4πR 2＝20π. 【答案】 20π 三、解答题(共46分)10．(15分)如果我们把体积和表面积数值相等的几何体叫做标准几何体，那么在正方体、等边圆柱(母线长等于底面圆直径的圆柱)、球三种几何体中有无这样的标准几何体？【解析】设正方体的棱长为a，则其体积V＝a3，表面积S＝6a2.由a3＝6a2，解得a＝6.所以当正方体的棱长为6时，它是标准几何体，设等边圆柱的底面半径为r，则其母线长为2r，它的体积V＝πr2×2r＝2πr3，表面积S＝2πr×2r＋2πr2＝6πr2.11．(15分)如图，已知几何体的三视图(单位：cm)．(1)画出这个几何体的直观图(不要求写画法)；(2)求这个几何体的表面积及体积．【解析】(1)这个几何体的直观图如图所示．(2)这个几何体可看成是由正方体AC1及直三棱柱B1C1Q-A1D1P的组合体．12. (16分)如图所示，以AB＝4 cm，BC＝3 cm的长方形ABCD为底面的长方体被平面斜着截断的几何体，EFGH是它的截面．当AE＝5 cm，BF＝8 cm，CG＝12 cm时，试回答下列问题：(1)求DH的长；(2)求这个几何体的体积；(3)截面四边形EFGH是什么图形？证明你的结论．【解析】(1)过E作EB1⊥BF，垂足为B1，则BB1=AE=5(cm)，所以B1F=8-5=3(cm)．因为平面ABFE∥平面DCGH，EF和HG是它们分别与截面的交线，所以EF∥HG.过H作HC1⊥CG，垂足为C1，则GC1=FB1=3(cm)，DH=12-3=9(cm)．(2)作ED1⊥DH，垂足为D1，B1P⊥CG，垂足为P，连结D1P，B1C1，则几何体被分割成一个长方体ABCD-EB1PD1，一个斜三棱柱EFB1-HGC1，一个直三棱柱EHD1-B1C1P.从而几何体的体积为(3)是菱形．证明：由(1)知EF∥HG，同理EH∥FG. 于是EFGH是平行四边形．所以EF=EH.故EFGH是菱形．。

空间几何体的结构及其表面积、体积一、选择题1．(2021·北京高考)某四面体的三视图如图所示,该四面体的表面积为( )A ．3＋32B ．12C ．1＋32D ．32A [根据图示三视图画正方体,删点,剩下的4个点就是三棱锥的顶点,如图所示,故S 表＝3×12×1×1＋34×(2)2＝3＋32． ]2．一个球的表面积是16π,那么这个球的体积为( ) A ．163π B ．323π C ．16π D ．24πB [设球的半径为R ,则S ＝4πR 2＝16π,解得R ＝2,则球的体积V ＝43πR 3＝323π．]3．用长为8,宽为4的矩形做侧面围成一个圆柱,则圆柱的轴截面的面积为( ) A ．32 B ．32π C ．16π D ．8πB [若8为底面周长,则圆柱的高为4,此时圆柱的底面直径为8π,其轴截面的面积为32π；若4为底面周长,则圆柱的高为8,此时圆柱的底面直径为4π,其轴截面的面积为32π．]4．(2020·全国卷Ⅰ)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A ．5－14 B ．5－12 C ．5＋14 D ．5＋12C [由题意知,可将金字塔看成如图所示的正四棱锥S ­ABCD ,其中M 为AD 的中点,O 为底面正方形ABCD 的中心,连接SM ,SO ,OM ,则SO ⊥底面ABCD ,SM ⊥AD ,OM ⊥AD ,即正四棱锥S ­ABCD 的高为SO ,侧面△SAD 的高为SM ．设底面正方形ABCD 的边长为a ,SM ＝h ,则OM ＝a 2,正四棱锥S ­ABCD 的一个侧面三角形的面积为12ah ,在Rt △SOM 中,SO 2＝SM 2－OM 2＝h 2－⎝ ⎛⎭⎪⎫a 22＝h 2－a 24,以该正四棱锥的高为边长的正方形的面积为SO 2＝h 2－a 24,故12ah ＝h 2－a 24,化简、整理得4h 2－2ah －a 2＝0,得4⎝ ⎛⎭⎪⎫h a 2－2⎝ ⎛⎭⎪⎫h a －1＝0,令h a ＝t ,则4t 2－2t －1＝0,因为t >0,所以t ＝1＋54,即h a ＝1＋54,所以其侧面三角形底边上的高与底面正方形的边长的比值为5＋14,故选C ．] 5．如图,正方体ABCD ­A 1B 1C 1D 1的棱长为1,E 为棱DD 1上的点,F 为AB 的中点,则三棱锥B 1­BFE 的体积为( )A ．13B ．14C ．112D ．16C [由等体积法可知VB 1­BFE＝VE ­BFB 1＝13S △BB 1F ·AD ＝16×1×12×1＝112．故选C ．] 6．古代数学名著《张丘建算经》中有如下问题：“今有仓,东西袤一丈二尺,南北广七尺,南壁高九尺,北壁高八尺,问受粟几何？”题目的意思是：有一粮仓的三视图如图所示(单位：尺),问能储存多少粟米．已知1斛米的体积约为1.62立方尺,估算粮仓可以储存的粟米约有(取整数)( )A ．410斛B ．420斛C ．430斛D ．441斛D [粮仓的形状为一个如图所示的直四棱柱,其体积为V ＝9＋82×7×12＝714(立方尺),又7141.62≈441,所以可以储存粟米约为441斛． ]7．(2021·全国卷甲)已知A ,B ,C 是半径为1的球O 的球面上的三个点,且AC ⊥BC ,AC ＝BC ＝1,则三棱锥O ­ABC 的体积为( )A ．212 B ．312 C ．24 D ．34A [如图所示,因为AC ⊥BC ,所以AB 为截面圆O 1的直径,且AB ＝2．连接OO 1,则OO 1⊥平面ABC ,OO 1＝1－⎝ ⎛⎭⎪⎫AB 22＝1－⎝ ⎛⎭⎪⎫222＝22,所以三棱锥O ­ABC 的体积V ＝13S △ABC ×OO 1＝13×12×1×1×22＝212．] 8．三棱锥P ­ABC 的四个顶点都在体积为500π3的球的表面上,底面ABC 所在的小圆面积为16π,则该三棱锥的高的最大值为( )A ．4B ．6C ．8D ．10C [依题意,设题中球的球心为O 、半径为R ,△ABC 的外接圆半径为r ,则4πR 33＝500π3,解得R ＝5,由πr 2＝16π,解得r ＝4,又球心O 到平面ABC 的距离为R 2－r 2＝3,因此三棱锥P ­ABC 的高的最大值为5＋3＝8,选C ．]二、填空题9．(2021·全国卷甲)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为________．39π [设该圆锥的高为h ,则由已知条件可得13×π×62×h ＝30π,解得h ＝52,则圆锥的母线长为h 2＋62＝254＋36＝132,故该圆锥的侧面积为π×6×132＝39π．] 10．有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC ＝45°,AB ＝AD ＝1,DC ⊥BC ,则这块菜地的面积为________．2＋22[如图①,在直观图中,过点A 作AE ⊥BC ,垂足为E ．图① 图②在Rt △ABE 中,AB ＝1,∠ABE ＝45°,∴BE ＝22． 而四边形AECD 为矩形,AD ＝1,∴EC ＝AD ＝1,∴BC ＝BE ＋EC ＝22＋1．由此可还原原图形如图②．在原图形中,A ′D ′＝1,A ′B ′＝2,B ′C ′＝22＋1,且A ′D ′∥B ′C ′,A ′B ′⊥B ′C ′,∴这块菜地的面积S ＝12(A ′D ′＋B ′C ′)×A ′B ′＝12×⎝ ⎛⎭⎪⎫1＋1＋22×2＝2＋22．] 11．圆台的上、下底面半径分别是10 cm 和20 cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积为________cm 2(结果中保留π)．1 100π [如图所示,设圆台的上底周长为C ,因为扇环的圆心角是180°,所以C ＝π·SA ．又C ＝2π×10＝20π,所以SA ＝20(cm)． 同理SB ＝40(cm)． 所以AB ＝SB －SA ＝20(cm)．S 表＝S 侧＋S 上底＋S 下底＝π(r 1＋r 2)·AB ＋πr 21＋πr 22＝π(10＋20)×20＋π×102＋π×202＝1 100π(cm 2)．故圆台的表面积为1 100π cm 2．]12．已知某圆锥的母线长为3,底面半径为1,则该圆锥的体积为________．设线段AB 为该圆锥底面圆的一条直径,一质点从A 出发,沿着该圆锥的侧面运动,到达B 点后再沿侧面回到A 点,则该质点运动路径的最短长度为________．22π3 6 [该圆锥的高h ＝32－1＝22． 所以该圆锥的体积V ＝13×π×12×22＝223π．将圆锥侧面沿母线SA 展开,如图所示．因为圆锥底面周长为2π,所以侧面展开后得到的扇形的圆心角∠ASA ′＝2π3．由题意知点B 是侧面展开后得到的扇形中弧AA ′的中点, 连接AB ,A ′B ,SB ,则∠ASB ＝π3,可得AB ＝A ′B ＝AS ＝3． 所以该质点运动路径的最短长度为AB ＋A ′B ＝6．]1．(2021·福州质检)如图,以棱长为1的正方体的顶点A 为球心,以2为半径作一个球面,则该正方体的表面被球面所截得的所有弧长之和为( )A ．3π4B ．2πC ．3π2D ．9π2C [正方体的表面被该球面所截得的弧长是相等的三部分,如图,上底面被球面截得的弧长是以A 1为圆心,1为半径的圆周长的14,所以所有弧长之和为3×2π4＝3π2．故选C ．]2．(2021·全国卷乙)以图①为主视图,在图②③④⑤中选两个分别作为左视图和俯视图,组成某个三棱锥的三视图,则所选左视图和俯视图的编号依次为________(写出符合要求的一组答案即可)．图① 图② 图③图④ 图⑤③④(答案不唯一,②⑤也可) [根据“长对正、高平齐、宽相等”及图中数据,可知图②③只能是左视图,图④⑤只能是俯视图,则组成某个三棱锥的三视图,所选左视图和俯视图的编号依次是③④或②⑤．若是③④,则原几何体如图1所示；若是②⑤,则原几何体如图2所示．图1 图2]。

课时规范练33基本立体图形及空间几何体的表面积和体积基础巩固组1.能旋转形成如图所示的几何体的平面图形是()2.用斜二测画法得到一个水平放置的平面图形OABC的直观图为如图所示的直角梯形O'A'B'C'，其中，若原平面图形OABC的面积为3√2，则O'A'的长为()梯形的上底长是下底长的13A.2B.√2C.√3D.323.如图所示的扇形是某个圆锥的侧面展开图，已知扇形所在圆的半径R=√5，扇形弧长l=4π，则该圆锥的表面积为()A.2πB.(4+2√5)πC.(3+√5)πD.8π+√54.(2021湖北十堰二模)已知某圆柱的轴截面是正方形，且该圆柱的侧面积是4π，则该圆柱的体积是()A.2πB.4πC.8πD.12π5.将半径为3，圆心角为2π3的扇形围成一个圆锥，则该圆锥的内切球的体积为()A.√2π3B.√3π3C.4π3D.2π6.(2021北京，8)定义:24小时内降水在平地上积水厚度(单位:mm)来判断降雨程度.其中小雨(<10 mm)，中雨(10 mm—25 mm)，大雨(25 mm—50 mm)，暴雨(50 mm—100 mm)，小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级()A.小雨B.中雨C.大雨D.暴雨7.下列四个论断不正确的是()A.过圆锥两母线的截面面积中，最大的不一定是轴截面面积B.经过一条已知直线有且只有一个平面与已知平面垂直C.等底面积等高的棱柱与圆柱的体积相等D.表面积相等的正方体和球体，体积较大的是球体8.(2021山东淄博一模)已知某圆锥底面圆的半径r=1，侧面展开图是一个半圆，则此圆锥的体积为.9.已知一个正四棱锥的侧棱与底面所成的角为45°，侧面积为4√3，则该棱锥的体积为.综合提升组10.如图，一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等，则下列结论正确的是()A.圆柱的体积为4πR3B.圆锥的侧面积为2πR2C.圆柱的侧面积与圆锥的表面积相等D.圆柱、圆锥、球的体积之比为3∶1∶211.用长度分别是2，3，5，6，9(单位:cm)的五根木棒连接(只允许连接，不允许折断)，组成共顶点的长方体的三条棱，则能够得到的对应长方体的最大表面积为()A.258 cm2B.414 cm2C.416 cm2D.418 cm212.(2021广东汕尾模拟)如图，一个圆锥形物体的母线长为6，一只小虫从圆锥的底面圆上的点P 出发，绕圆锥表面爬行一周后回到点P处.若该小虫爬行的最短路程为6√2，则该圆锥形物体的底面半径为.13.如图，在长方体ABCD-A1B1C1D1中，AB=14，BC=5，AA1=4，点E，F分别在A1B1，D1C1上，A1E=D1F=2.(1)求直线CF与C1E所成角的余弦值;(2)过点E，F的平面α与此长方体的表面相交，交线围成一个正方形，求平面α把该长方体分成的较小部分与较大部分的体积的比值.创新应用组14.有一种外形为圆锥形的斗笠，称为“灯罩斗笠”，根据人的体型、高矮等制作成大小不一的型号供人选择使用，不同型号的斗笠大小经常用帽坡长(母线长)和帽底宽(底面圆直径长)两个指标进行衡量，现有一个“灯罩斗笠”，帽坡长20厘米，帽底宽20√3厘米，关于此斗笠，下面说法错误的是()A.分笠轴截面(过顶点和底面中心的截面图形)的顶角为120°B.过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为100√3平方厘米C.若此斗笠顶点和底面圆上所有点都在同一个球上，则该球的表面积为1 600π平方厘米D.此斗笠放在平面上，可以盖住的球(保持斗笠不变形)的最大半径为(20√3-30)厘米15.(2021八省联考模拟卷)用曲率刻画空间弯曲性，规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫作多面体的面角，角度用弧度制)，多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角，每个面角是π3，所以正四面体在各顶点的曲率为2π-3×π3=π，故其总曲率为4π.(1)求四棱锥的总曲率;(2)若多面体满足:顶点数-棱数+面数=2，证明:这类多面体的总曲率是常数.课时规范练33 基本立体图形及空间几何体的表面积和体积1.A 解析:此几何体自上向下是由一个圆锥、两个圆台和一个圆柱构成，是由A 中的平面图形旋转形成的.故选A .2.D 解析:设O'A'=x ，则O'B'=√2x ，在原图形中OB=2O'B'=2√2x ，BC=B'C'=x3，OA=O'A'=x ，OB 为原图形中梯形的高，面积为S=12×x+13x ×2√2x=3√2，解得x=32，故选D .3.B 解析:设圆锥底面圆半径为r ，则2πr=4π，解得r=2.圆锥的表面积S 表=S 底面圆+S 侧=πr 2+12lR=π×22+12×4π×√5=(4+2√5)π. 故选B .4.A 解析:设该圆柱的底面圆半径为r ，则圆柱的高(母线)为h ，而圆柱的轴截面是正方形，则h=2r ，圆柱侧面积为2πrh=4π，即4πr 2=4π，解得r=1，h=2，故该圆柱的体积是πr 2h=2π. 故选A .5.A 解析:设圆锥的底面半径为r ，高为h ，则2πr=2π3×3，所以r=1，则h=√32-12=2√2. 设内切球的半径为R ，则R2√2-R=13，所以R=√22，所以V=4π3R 3=4π3×√223=√2π3.故选A .6.B 解析:由题可知，圆锥内积水的高度是圆锥高度的一半，则圆锥内积水部分的半径为r=12×12×200=50(mm)，h=12×300=150(mm).所以由定义可得，积水厚度d=13π×502×150π×1002=12.5(mm)，属于中雨.故选B .7.B 解析:由于圆锥母线长度都相等由于圆锥母线长度都相等，设两母线的夹角为θ，母线长为2，则过圆锥两母线的截面面积为12×2×2sin θ=2sin θ，当轴截面两母线的夹角θ=150°时，轴截面的面积为2sin150°=1，此时可以找到一个两母线的夹角θ=90°不是轴截面的截面，其面积为2sin90°=2，故A 正确;当已知直线垂直于已知平面时，过已知直线的所有平面都垂直于已知平面，故B 错误;由于棱柱和圆柱的体积都是底面积乘高，则等底面积等高的棱柱与圆柱的体积相等，故C 正确;设正方体的棱长为a ，球的半径为R ，则S=4πR 2=6a 2，球的体积为V 1=43×πR 3=S 3×√S4π，正方体的体积为V 2=a 3=S 6×√S6，所以V 1>V 2，故D 正确.故选B . 8.√3π3解析:∵圆锥的侧面展开图是一个半圆，圆锥的底面周长为2π，即侧面展开图半圆的弧长是2π，则半圆的半径，即圆锥的母线为2. 圆锥的高为√22-12=√3. ∴圆锥的体积V=13π×12×√3=√3π3. 9.4√23解析:设正四棱锥底面边长为2a ，且正四棱锥的侧棱与底面所成的角为45°，则四棱锥的高为√2a.又正四棱锥的侧面积为4√3，所以每个侧面的面积为√3. 则12×2a ×√3a=√3，解得a=1.即正四棱锥的高为√2，故该棱锥的体积为13×22×√2=4√23. 10.D 解析:依题意圆柱的底面半径为R ，则圆柱的高为2R ，故圆柱的体积为πR 2×2R=2πR 3，故A 错误;由题可得，圆锥的母线长为√5R ，圆锥的侧面积为πR ×√5R=√5πR 2，故B 错误; ∵圆柱的侧面积为4πR 2，圆锥表面积为√5πR 2+πR 2，故C 错误; ∴V 圆柱=πR 2·2R=2πR 3，V 圆锥=13πR 2·2R=23πR 3，V 球=43πR 3，∴V 圆柱∶V 圆锥∶V 球=2πR 3∶23πR 3∶43πR 3=3∶1∶2，故D 正确.故选D .11.C 解析:设长方体的三条棱的长度为a ，b ，c ， 所以长方体表面积S=2(ab+bc+ac )≤(a+b)22+(b+c)22+(a+c)22，当且仅当a=b=c 时取等号又由题意可知a=b=c 不可能成立，所以当a ，b ，c 的长度最接近时，此时对应的表面积最大，此时三边长分别为8cm ，8cm ，9cm ， 用2cm 和6cm 连接在一起形成8cm ，用3cm 和5cm 连接在一起形成8cm ，剩余一条棱长为9cm ， 所以最大表面积为2×(8×8+8×9+8×9)=416(cm 2).故选C .12.32解析:圆锥侧面展开图为扇形POP'，如图.由题知，OP=OP'=6，小虫爬行的最短路程为线段PP'，即PP'=6√2.显然有OP2+OP'2=72=PP'2，即∠POP'=π2.设圆锥底面圆半径为r，则有2πr=6×π2=3π，解得r=32.即圆锥形物体的底面半径为32.13.解(1)连接EF，EB，BC1，长方体ABCD-A1B1C1D1中，A1E=D1F=2，且A1E∥D1F，所以四边形A1EFD1是平行四边形，所以A1D1与EF平行且相等，所以EF与BC平行且相等，所以四边形EFCB为平行四边形，所以FC∥BE，直线CF与C1E所成角就是∠C1EB或其补角，C1E=√EF2+FC12=13，EB=√EB12+BB12=4√10，C1B=√B1B2+B1C12=√41，在△C1EB中，由余弦定理，cos∠C1EB=C1E 2+EB2-C1B22C1E·EB =2×13×4√10=18√1065，所以直线CF与C1E所成角的余弦值为18√1065.(2)设过点E，F的平面α与此长方体的表面相交，交线围成一个正方形，即正方形EFNM，则EM=5，作EP⊥AB于点P，作FQ⊥DC于点Q，所以PM=3，所以点M在点P的右侧，平面α把该长方体分成的两部分为直棱柱AMEA1-DNFD1和直棱柱EMBB1-FNCC1，两个直棱柱的高相等，两部分体积之比为V AMEA 1-DNFD 1VEMBB 1-FNCC 1=AM+A 1E2·AA 1·AD MB+B 1E2·AA 1·BC=721=13.14.B 解析:对于A ，作出图形如图所示，PO=√202-(10√3)2=√400−300=10， 所以sin ∠APO=AO AP=10√320=√32， 因为0°<∠APO<90°，故∠APO=60°，所以∠APB=120°，故选项A 正确;对于B ，设∠APB=θ，截面三角形面积为S=12·PA 2·sin θ=200sin θ≤200，故选项B 不正确; 对于C ，设外接球球心为M ，半径为R ，所以MA=MP=R ， 在△AOM 中，由勾股定理可得300+(R-10)2=R 2，解得R=20， 所以该球的表面积S=4π×202=1600π，故选项C 正确;对于D ，设球心为O'，截面主视图如图所示，设内切圆半径为r ，△ABP 各边长分别为PA=PB=20，AB=20√3，所以12×(20+20+20√3)r=12×20√3×10， 解得r=20√3-30，故选项D 正确.故选B .15.(1)解由题可知，四棱锥的总曲率等于四棱锥各顶点的曲率之和.可以从整个多面体的角度考虑，所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知，四棱锥共有5个顶点，5个面，其中4个为三角形，1个为四边形.所以四棱锥的表面内角和由4个为三角形，1个为四边形组成，则其总曲率为2π×5-(4π+2π)=4π.(2)证明设顶点数、棱数、面数分别为n，l，m，所以有n-l+m=2.设第i个面的棱数为x i，所以x1+x2+…+x m=2l，所以总曲率为2πn-π[(x1-2)+(x2-2)+…+(x m-2)]=2πn-π(2l-2m)=2π(n-l+m)=4π，所以这类多面体的总曲率是常数.11。

高考数学一轮复习简单几何体的表面积和体积课时作业35文北师大版一、选择题1．(2010年安徽高考)一个几何体的三视图如图，该几何体的表面积为( )A．280 B．292C．360 D．372解析：该几何体的直观图如图．∴S表＝2(2×8＋8×10＋2×10)＋2(8×6＋8×2)＝360，故选C.答案：C2．(2010年北京高考)如图，正方体ABCD－A1B1C1D1的棱长为2，动点E，F在棱A1B1上，动点P，Q分别在棱AD，CD上．若EF＝1，A1E＝x，DQ＝y，DP＝z(x，y，z大于零)，则四面体PEFQ的体积( )A ．与x ，y ，z 都有关B ．与x 有关，与y ，z 无关C ．与y 有关，与x ，z 无关D ．与z 有关，与x ，y 无关 解析：∵DC ∥A 1B 1，EF ＝1， ∴S △EFQ ＝12×1×22＝2(定值)．四面体PEFQ 中面EFQ 上的高为P 到面A 1DCB 1的距离，为DP ·sin45°＝22z .∴V 四面体PEFQ＝13×2×22z ＝13z . 答案：D3．一个多面体的三视图分别为正方形、等腰三角形和矩形，如图所示，则该多面体的体积为( )A ．24 cm 3B ．48 cm 3C ．32 cm 3D ．28 cm 3解析：几何体是一个直三棱柱，其体积等于12×6×4×4＝48(cm 3)．答案：B4．已知某几何体的三视图如图，其中正(主)视图中半圆的半径为1，则该几何体的体积为( )A ．24－3π2B ．24－π3C ．24－πD ．24－π2解析：该几何体是一个长方体挖去一个半圆柱体，其体积等于3×2×4－3×12×π×12＝24－3π2.答案：A5．一个正方体的体积是8，则这个正方体的内切球的表面积是( ) A ．8π B ．6π C ．4πD ．π解析：设正方体的棱长为a ，则a 3＝8，∴a ＝2.而此正方体的内切球直径为2，∴S 表＝4πr 2＝4π.答案：C6．某几何体的三视图如图所示，则该几何体的体积等于( )A.283π B.163π C.43π＋8 D ．12π解析：由三视图可知，该几何体为底面半径是2，高为2的圆柱体和半径为1的球体的组合体，则该几何体的体积为π×22×2＋43π＝283π.答案：A 二、填空题7． [2011·福建卷] 三棱锥P －ABC 中，PA ⊥底面ABC ，PA ＝3，底面ABC 是边长为2的正三角形，则三棱锥P －ABC 的体积等于________．解析：由已知，S △ABC ＝12×22sin π3＝3，∴ V P －ABC ＝13S △ABC ·PA ＝13×3×3＝3，即三棱锥P －ABC 的体积等于 3.答案： 38．(2010年江西高考)如图，在三棱锥O －ABC 中，三条棱OA ，OB ，OC 两两垂直，且OA >OB >OC ，分别经过三条棱OA ，OB ，OC 作一个截面平分三棱锥的体积，截面面积依次为S 1，S 2，S 3，则S 1，S 2，S 3的大小关系为________．解析：取BC 中点D ，AB 中点E ，AC 中点F ，易知面AOD ，面BOF ，面COE 平分三棱锥的体积．S 1＝S △AOD ，S 2＝S △BOF ，S 3＝S △COE .设OA ＝a ，OB ＝b ，OC ＝c ，则S 1＝12a ·OD ＝12a ·12BC ＝14a ·b 2＋c 2＝14a 2b 2＋a 2c 2.同理S 2＝14a 2b 2＋b 2c 2，S 3＝14a 2c 2＋b 2c 2.∵a >b >c ，∴S 1>S 2>S 3. 答案：S 3<S 2<S 19．(2010年湖北高考)圆柱形容器内部盛有高度为8 cm 的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是________cm.解析：设球的半径为r ，则6r ·πr 2＝8πr 2＋3×43πr 3⇒r ＝4(cm)．答案：4 三、解答题10．已知正方体AC 1的棱长为a ，E 、F 分别为棱AA 1与CC 1的中点，求四棱锥A 1－EBFD 1的体积．解：因为EB ＝BF ＝FD 1＝D 1E ＝a 2＋a22＝52a ， 所以四棱锥A 1－EBFD 1的底面是菱形，连接EF ， 则△EFB ≌△EFD 1，由于三棱锥A 1－EFB 与三棱锥A 1－EFD 1等底同高， 所以VA 1－EBFD 1＝2VA 1－EFB ＝2VF －EBA 1 ＝2·13·S △EBA 1·a ＝16a 3.11．如图，已知某几何体的三视图如下(单位：cm)．(1)画出这个几何体的直观图(不要求写画法)； (2)求这个几何体的表面积及体积． 解：(1)这个几何体的直观图如图所示．(2)这个几何体可看成是正方体AC 1及直三棱柱B 1C 1Q －A 1D 1P 的组合体． 由PA 1＝PD 1＝2，A 1D 1＝AD ＝2， 可得PA 1⊥PD 1. 故所求几何体的表面积S ＝5×22＋2×2×2＋2×12×(2)2＝22＋42(cm 2)，所求几何体的体积V ＝23＋12×(2)2×2＝10(cm 3)．12．一几何体按比例绘制的三视图如图所示(单位：m)：(1)试画出它的直观图；(2)求它的表面积和体积． 解：(1)直观图如图所示：(2)解法一：由三视图可知该几何体是长方体被截去一个角，且该几何体的体积是以A 1A ，A 1D 1，A 1B 1为棱的长方体的体积为34，在直角梯形AA 1B 1B 中，作BE ⊥A 1B 1于E ， 则AA 1EB 是正方形，∴AA 1＝BE ＝1.在Rt △BEB 1中，BE ＝1，EB 1＝1，∴BB 1＝ 2. ∴几何体的表面积S ＝S 正方形AA 1D 1D ＋2S 梯形AA 1B 1B ＋S 矩形BB 1C 1C ＋S 正方形ABCD ＋S 矩形A 1B 1C 1D 1＝1＋2×12×(1＋2)×1＋1×2＋1＋1×2＝7＋2(m 2)．∴几何体的体积V ＝34×1×2×1＝32(m 3)，∴该几何体的表面积为(7＋2)m 2，体积为32m 3.解法二：几何体也可以看作是以AA 1B 1B 为底面的直四棱柱，其表面积求法同解法一，V 直四棱柱D 1C 1CD －A 1B 1BA ＝Sh＝12×(1＋2)×1×1＝32(m 3)． ∴几何体的表面积为(7＋2)m 2，体积为32m 3.。

第五节简单几何体的面积和体积对应学生用书P1141．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r ＋r ′)l2．空间几何体的表面积与体积公式名称 几何体表面积 体积 柱体(棱柱和圆柱) S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥) S 表面积＝S 侧＋S 底 V ＝13Sh台体(棱台和圆台)S 表面积＝S 侧＋S 上＋S 下V ＝13(S 上＋S 下＋S 上S 下)h球S ＝4πR 2V ＝43πR 31．求组合体的表面积时：组合体的衔接部分的面积问题易出错．2．由三视图计算几何体的表面积与体积时，由于几何体的还原不准确及几何体的结构特征认识不准易导致失误．3．易混左面积与表面积的概念． [试一试]1．若某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是( )A ．(13＋2)π(cm 2)B ．4＋(13＋2)π(cm 2)C ．6＋(13＋2)π(cm 2)D ．8＋(13＋2)π(cm 2)解析：选C 由三视图可知原几何体是一个半圆锥，其表面积S ＝12×π×22＋12×π×2×13＋12×4×3＝6＋(13＋2)π(cm 2)． 2.一个几何体的三视图如图所示，其中主视图是一个正三角形，则该几何体的体积为( )A.33B ．1 C.233D. 3解析：选A 根据三视图可知该几何体是一个高为3的三棱锥，所以该几何体的体积V ＝13×⎝⎛⎭⎫12×2×1×3＝33. 3．若某几何体的三视图如图所示，则此几何体的表面积是________．解析：由三视图可知，该几何体由一个正四棱柱和一个棱台组成，其表面积S ＝3×4×2＋2×2×2＋4×22×2＋4×6＋12×(2＋6)×2×2＝72＋16 2.答案：72＋16 21．求空间几何体体积的常用方法(1)公式法：直接根据相关的体积公式计算．(2)等积法：根据体积计算公式，通过转换空间几何体的底面和高使得体积计算更容易，或是求出一些体积比等．(3)割补法：把不能直接计算体积的空间几何体进行适当的分割或补形，转化为可计算体积的几何体．2．几个与球有关的切、接常用结论 (1)正方体的棱长为a ，球的半径为R ， ①正方体的外接球，则2R ＝3a ； ②正方体的内切球，则2R ＝a ； ③球与正方体的各棱相切，则2R ＝2a .(2)长方体的同一顶点的三条棱长分别为a ，b ，c ，外接球的半径为R ，则2R ＝a 2＋b 2＋c 2. (3)正四面体的外接球与内切球的半径之比为3∶1. 3．旋转体侧面积问题中的转化思想计算旋转体的侧面积时，一般采用转化的方法来进行，即将侧面展开化为平面图形，“化曲为直”来解决，因此要熟悉常见旋转体的侧面展开图的形状及平面图形面积的求法．[练一练]1．(2014·皖南八校联考)已知某几何体的左视图与其主视图相同，相关的尺寸如图所示，则这个几何体的体积是( )A ．8πB ．7πC ．2πD.7π4解析：选D 依题意该几何体为一空心圆柱，故其体积V ＝π⎣⎡⎦⎤22－⎝⎛⎭⎫322×1＝7π4. 2．(2013·福建高考改编)已知某一多面体内接于球构成一个简单组合体，如果该组合体的主视图、左视图、俯视图均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是________．解析：依题意得，该几何体是球的一个内接正方体，且该正方体的棱长为2.设该球的直径为2R ，则2R ＝22＋22＋22＝23，所以该几何体的表面积为4πR 2＝4π(3)2＝12π.答案：12π对应学生用书P115考点一几何体的表面积1．(2013·重庆高考改编)某几何体的三视图如图所示，则该几何体的表面积为()A．180B．200C．220 D．240解析：选D由三视图可知，此几何体是一个横放的直四棱柱，底面梯形的面积为(2＋8)×42＝20，侧面面积为2×10＋2×5×10＋8×10＝200，故四棱柱的表面积为2×20＋200＝240.2．(2013·陕西高考改编)某几何体的三视图如图所示，则其表面积为________解析：此几何体是一个半球，所以表面积为球的表面积的一半加上底面的面积，球半径为1，故所求表面积为S＝2π＋π＝3π.答案：3π3．(2014·江西八校联考)若一个圆台的主视图如图所示，则其表面积等于________．解析：由图知圆台的上、下底面半径分别为r＝1、r′＝2，母线长为l＝5，则圆台表面积为π(r＋r′)l＋π(r2＋r′2)＝5π＋35π.答案：5π＋35π[类题通法]以三视图为载体的几何体的表面积问题的求法(1)恰当分析给出的三视图．(2)找准几何体中各元素间的位置关系及数量关系．(3)注意组合体的表面积问题中重合部分的处理．考点二几何体的体积[典例](1)如图所示，已知三棱柱ABC-A 1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1 -ABC1的体积为()A.312 B.34C.612 D.64(2)(2013·北京高考改编)某四棱锥的三视图如图所示，该四棱锥的体积为________．[解析](1)三棱锥B1 -ABC1的体积等于三棱锥A -B1BC1的体积，三棱锥A -B1BC1的高为3 2，底面积为12，故其体积为13×12×32＝312.(2)由三视图可知直观图是一个底面为边长等于3的正方形，高为1的四棱锥，由棱锥的体积公式得V四棱锥＝13×32×1＝3.[答案](1)A(2)3[类题通法]求解几何体体积的策略及注意问题(1)与三视图有关的体积问题关键是准确还原几何体及弄清几何体中的数量关系．(2)计算柱、锥、台的体积关键是根据条件找出相应的底面积和高．(3)注意求体积的一些特殊方法：分割法、补体法、转化法等，它们是解决一些不规则几何体体积计算常用的方法，应熟练掌握．(4)注意组合体的组成形式及各部分几何体的特征．[针对训练](2014·绍兴模拟)已知一个棱长为2的正方体，被一个平面截后所得几何体的三视图如图所示，则该几何体的体积是________．解析：根据三视图，我们先画出其几何直观图，几何体由正方体切割而成，即正方体截去一个棱台．如图1所示，把棱台补成锥体如图2，V 棱台＝2×2×12×4×13－1×1×12×2×13＝73，故所求几何体的体积V ＝23－73＝173.答案：173考点三与球有关的切、接问题与球相关的切、接问题是高考命题的热点，也是考生的难点、易失分点.命题角度多变.归纳起来常见的命题角度有：(1)直三棱柱的外接球； (2)正(长)方体的外接球； (3)正四面体的内切球；(4)四棱锥的外接球.角度一 直三棱柱的外接球1．(2013·辽宁高考)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( )A.3172B ．210 C.132D ．310解析：选C 如图，由球心作平面ABC 的垂线，则垂足为BC 的中点M .又AM ＝12BC ＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA ＝⎝⎛⎭⎫522＋62＝132. 角度二 正方体的外接球2．(2013·合肥模拟)一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为2的正方形)，则该几何体外接球的体积为________．解析：依题意可知，新的几何体的外接球也就是原正方体的外接球，要求的直径就是正方体的体对角线；∴2R ＝23(R 为球的半径)，∴R ＝3，∴球的体积V ＝43πR 3＝43π.答案：43π角度三 正四面体的内切球3．(2014·长春模拟)若一个正四面体的表面积为S 1，其内切球的表面积为S 2，则S 1S 2＝________.解析：设正四面体棱长为a ，则正四面体表面积为S 1＝4·34·a 2＝3a 2，其内切球半径为正四面体高的14，即r ＝14·63a ＝612a ，因此内切球表面积为S 2＝4πr 2＝πa 26，则S 1S 2＝3a 2π6a 2＝63π. 答案：63π角度四四棱锥的外接球4．四棱锥P-ABCD的五个顶点都在一个球面上，该四棱锥的三视图如图所示，E，F分别是棱AB，CD的中点，直线EF被球面所截得的线段长为22，则该球的表面积为()A．9π B．3πC．22π D．12π解析：选D该几何体的直观图如图所示，该几何体可看作由正方体截得，则正方体外接球的直径即为PC.由直线EF被球面所截得的线段长为22，可知正方形ABCD对角线AC的长为22，可得a＝2，在△P AC中PC＝22＋(22)2＝23，球的半径R＝3，∴S表＝4πR2＝4π×(3)2＝12π.[类题通法]解决与球有关的切、接问题的方法(1)一般要过球心及多面体中的特殊点或过线作截面将空间问题转化为平面问题，从而寻找几何体各元素之间的关系．(2)若球面上四点P，A，B，C中P A，PB，PC两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正方体确定直径解决外接问题．对应学生用书P117[课堂练通考点]1．(2013·济南模拟)一个几何体的三视图如图所示，则它的体积为()A.203 B.403 C ．20D ．40解析：选B 该空间几何体是一个四棱锥，其直观图如图所示．其体积为13×12(1＋4)×4×4＝403.2．(2014·临沂模拟)一个几何体的三视图如图所示，则该几何体的体积是( )A ．6B ．8C ．10D ．12解析：选D 该几何体是一个长方体在左边挖去一个三棱柱再拼接到右边而得到的，它的体积就是长方体的体积，体积为V ＝(2.4＋0.6)×2×(1＋1)＝12.3．(2014·湖北八校联考)已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为V 1，直径为4的球的体积为V 2，则V 1∶V 2＝________.解析：由三视图知，该几何体为圆柱内挖去一个底面相同的圆锥，因此V 1＝8π－8π3＝16π3，V 2＝4π3×23＝32π3，V 1∶V 2＝1∶2.答案：1∶24．已知三棱锥O -ABC 中，∠BOC ＝90°，OA ⊥平面BOC ，其中AB ＝AC ＝7，BC ＝11，O ，A ，B ，C 四点均在球S 的表面上，则球S 的表面积为________．解析：易知以O 点为顶点的三条棱两两垂直，则球S 即为以O 为顶点，以OA ，OB ，OC 为棱的长方体的外接球，所以2R ＝OA 2＋OB 2＋OC 2＝12×2(OA 2＋OB 2＋OC 2)＝522(R 为球S 的半径)，所以R ＝524，表面积S ＝4πR 2＝25π2.答案：25π25．(2013·郑州模拟)已知三棱锥S -ABC 的所有顶点都在球O 的球面上，SA ⊥平面ABC ，SA ＝23，AB ＝1，AC ＝2，∠BAC ＝60°，求球O 的表面积．解：取SC 的中点E ，连接AE ，BE ，依题意，BC 2＝AB 2＋AC 2－2AB ·AC cos 60°＝3，∴AC 2＝AB 2＋BC 2，即AB ⊥BC .又SA ⊥平面ABC ，∴SA ⊥BC ，又SA ∩AB ＝A ，∴BC ⊥平面SAB ，BC ⊥SB ，AE ＝12SC ＝BE ，∴点E 是三棱锥S -ABC 的外接球的球心，即点E 与点O 重合，OA＝12SC ＝12SA 2＋AC 2＝2，球O 的表面积为4π×OA 2＝16π.[课下提升考能]第Ⅰ组：全员必做题1．正六棱柱的高为6，底面边长为4，则它的全面积为( ) A ．48(3＋3) B ．48(3＋23) C ．24(6＋2) D ．144解析：选A S 底＝6×34×42＝243，S 侧＝6×4×6＝144，∴S 全＝S 侧＋2S 底＝144＋483＝48(3＋3)．2．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为( )A ．7B ．6C ．5D ．3解析：选A 设圆台较小底面半径为r ， 则另一底面半径为3r .由S ＝π(r ＋3r )·3＝84π，解得r ＝7.3．(2013·深圳调研)如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积、体积分别是( )A ．32π，128π3B ．16π，32π3C ．12π，16π3D ．8π，16π3解析：选C 根据三视图可知，该几何体是一个半球，且半径为2，故其表面积S ＝12(4×π×22)＋π×22＝12π，体积V ＝12⎝⎛⎭⎫43×π×23＝16π3. 4．设长方体的长、宽、高分别为2a ，a ，a ，其顶点都在一个球面上，则该球的表面积为( )A ．3πa 2B ．6πa 2C ．12πa 2D ．24πa 2解析：选B 由于长方体的长、宽、高分别为2a ，a ，a ，则长方体的体对角线长为(2a )2＋a 2＋a 2＝6a .又长方体外接球的直径2R 等于长方体的体对角线，∴2R ＝6a .∴S 球＝4πR 2＝6πa 2.5．(2013·洛阳统考)如图是某几何体的三视图，则该几何体的体积为( )A ．64＋32πB ．64＋64πC ．256＋64πD ．256＋128π解析：选C 依题意，该几何体是一个正四棱柱及一个圆柱的组合体，其中正四棱柱的底面边长是8、侧棱长是4，圆柱的底面半径是4、高是4，因此所求几何体的体积等于π×42×4＋82×4＝256＋64π，选C.6．某几何体的三视图如图所示，则其体积为________．解析：易知原几何体是底面圆半径为1，高为2的圆锥体的一半，故所求体积为V ＝12×13×(π×12)×2＝π3.答案：π37．(2014·杭州模拟)若某几何体的三视图(单位：cm)如图所示，则此几何体的体积等于________cm 3.解析：根据三视图，几何体是一个三棱柱削去一个三棱锥，体积V ＝12×3×4×5－13×12×4×3×3＝24 cm 3.答案：248.(创新题)如图，在三棱锥D -ABC 中，已知BC ⊥AD ，BC ＝2，AD ＝6，AB ＋BD ＝AC ＋CD ＝10，则三棱锥D -ABC 的体积的最大值是________．解析：由题意知，线段AB ＋BD 与线段AC ＋CD 的长度是定值，因为棱AD 与棱BC 相互垂直．设d 为AD 到BC 的距离．则V D －ABC ＝AD ·BC ×d ×12×13＝2d ，当d 最大时，V D －ABC 体积最大， ∵AB ＋BD ＝AC ＋CD ＝10，∴当AB ＝BD ＝AC ＝CD ＝5时， d 有最大值42－1＝15.此时V ＝215. 答案：2159．一个几何体的三视图如图所示．已知主视图是底边长为1的平行四边形，左视图是一个长为3、宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．(1)求该几何体的体积V ； (2)求该几何体的表面积S .解：(1)由三视图可知，该几何体是一个平行六面体(如图)，其底面是边长为1的正方形，高为3，所以V ＝1×1×3＝ 3.(2)由三视图可知，该平行六面体中，A 1D ⊥平面ABCD ，CD ⊥平面BCC 1B 1，所以AA 1＝2，侧面ABB 1A 1，CDD 1C 1均为矩形．S ＝2×(1×1＋1×3＋1×2)＝6＋2 3.10．(2014·徐州质检)如图，在直三棱柱ABC -A 1B 1C 1中，AB ＝AC ＝5，BB 1＝BC ＝6，D ，E 分别是AA 1和B 1C 的中点．(1)求证：DE ∥平面ABC ； (2)求三棱锥E -BCD 的体积．解：(1)证明：如图，取BC 的中点G ，连接AG ，EG ，因为E 是B 1C 的中点，所以EG ∥BB 1，且EG ＝12BB 1.由题意知，AA 1綊BB 1.而D 是AA 1的中点，所以EG 綊AD . 所以四边形EGAD 是平行四边形． 所以ED ∥AG .又DE ⊄平面ABC ，AG ⊂平面ABC ， 所以DE ∥平面ABC .(2)因为AD ∥BB 1，所以AD ∥平面BCE . 所以V E -BCD ＝V D -BCE ＝V A -BCE ＝V E -ABC . 由(1)知，DE ∥平面ABC ，所以V E -BCD ＝V E -ABC ＝V D -ABC ＝13AD ·12BC ·AG ＝16×3×6×4＝12. 第Ⅱ组：重点选做题1．(2013·昆明调研)如图，若一个空间几何体的三视图中，主视图和左视图都是直角三角形，其直角边长均为1，则该几何体的表面积为( )A ．1＋ 2B ．2＋2 2 C.13 D ．2＋ 2解析：选D 依题意得，题中的几何体是底面为正方形，侧棱垂直于底面的四棱锥P -ABCD (如图)，其中底面边长为1，PD ＝1，PD ⊥平面ABCD ，S △P AD ＝S △PCD ＝12×1×1＝12，S △P AB ＝S △PBC ＝12×1×2＝22，S四边形ABCD ＝12＝1，因此该几何体的表面积为2＋2，选D.2．.(2014·绍兴模拟)已知正四面体的俯视图如图所示，其中四边形ABCD 是边长为2的正方形，则这个正四面体的体积为________．解析：由题意知BD 为实长，即正四面体的边长为22， 所以S ＝34·(22)2＝23， h ＝(22)2－⎝⎛⎭⎫2632＝433，故V ＝13·S ·h ＝13×23×433＝83.答案：83。

课时44 几何体的表面积与体积(课前预习案)班级： 姓名：一、高考考纲要求了解球、棱柱、棱锥、台的表面积和体积的计算公式（不要求记忆公式）. 二、高考考点回顾1. 多面体与旋转体的结构特征结 构 特 征结 构 特 征图例棱柱（1）两底面相互平行，其余各面都是平行四边形； （2）侧棱平行且相等. 圆柱（1）两底面相互平行；（2）侧面的母线平行于圆柱的轴；（3）是以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的几何体.棱锥（1）底面是多边形，各侧面均是三角形； （2）各侧面有一个公共顶点.圆锥（1）底面是圆；（2）是以直角三角形的一条直角边所在的直线为旋转轴，其余两边旋转形成的曲面所围成的几何体.棱台（1）两底面相互平行；（2）是用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分.圆台 （1）两底面相互平行；（2）是用一个平行于圆锥底面的平面去截圆锥，底面和截面之间的部分.球（1）球心到球面上各点的距离相等；（2）是以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体.2.（1）直棱柱：侧棱与底面 .（2）正棱柱：底面为 ;侧棱与底面 .（3）正棱锥：底面为 ，顶点和底面中心的连线与底面 . 2.几何体的表面积与体积公式面积公式：表面积相关公式 表面积相关公式棱柱 2S S S =+侧全底圆柱222S r rh ππ=+全 （r ：底面半径，h ：高） 棱锥 S S S =+全侧底 圆锥2S r rl ππ=+全 （r ：底面半径，l ：母线长） 棱台 S S S S =++全侧上底下底圆台 22('')S r r r l rl π=+++全 （r ：下底半径，'r ：上底半径，l ：母线长） 球 2=4S R π球面体积公式体积公式棱柱 V S h =g 底高圆柱 2V r h π= 棱锥13V S h =g 底高圆锥21=3V r h π4.组合体的表面积与体积：注意组合体表面与体积的构成，将其分割为多个规则几何体求解.三、课前检测1. 一个棱柱是正四棱柱的条件是（）A.底面是正方形有两个侧面是矩形B.底面是正方形，两个侧面垂直于底面C.底面是菱形且有一个顶点处的两条棱互相垂直D.底面是正方形，每个侧面都是全等矩形的四棱柱2. 底面半径为2的圆柱的表面积为16π，则其母线长为（）A.1B.4C.2D.63.一个棱柱，其侧面为矩形，底面是菱形，且菱形的两条对角线长分别是6cm和8cm，侧棱长是5cm，则这个直棱柱的侧面积是（）A. 100 cm2B. 200 cm2C. 2D. cm24.将底面半径和高均为3cm的圆柱状铜块熔化后铸成一个正方体铜块，则该正方体的棱长等于（） A.B. D.5．已知圆台的上下底面半径分别是2、5，且侧面面积等于两底面面积之和，求该圆台的母线长.课内探究案班级：姓名：考点一：简单几何体的表面积与体积【典例1】已知直四棱柱的底面为菱形，两个对角面的面积分别为22cm、2，侧棱长为2cm ，求其体积.【变式1】（1）(2013江苏)如图，在三棱柱111A B C ABC -中，D ，E ，F 分别为AB ，AC ，1AA 的中点，设三棱锥F ADE -体积为1V ，三棱柱111A B C ABC -的体积为2V ，则12:V V = .(2)已知H 是球O 的直径AB 上一点，:1:2AH HB =，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为_______.考点二：组合体的表面积与体积【典例2】如图几何体中，正四棱柱的底边边长为2，高为1，半球的下底面内切于正四棱柱的上底面，试求该222正视图俯视图侧视图几何体的表面积和体积.【变式2】（1）三角形ABC 中， 90,3,1B AB BC ∠===o，以边AB 所在直线为旋转轴，其余各边旋转一周而形成的曲面所围成的几何体的体积为（ ）A. πB. 2πC. 3πD.3π（2）如图正三棱柱的底面边长和高均为2，D 、E 分别是11A B 与11A C 的中点.试求截面ADE 右侧六面体的体积.C考点三：三视图与几何体的表面积与体积【典例3】（1）如图是一个几何体的三视图，侧视图是一个等边三角形，根据尺寸（单位：cm ）可知这个几何体的表面积为（ ）C.2(1823)cm +D.2(623)cm + （2）若某几何体的三视图 (单位：cm)如图所示，则此几何体的体积是 cm 3.【变式3】（1）已知一个几何体的三视图如图所示(单位：cm)， 其中正视图是直角梯形，侧视图和俯视图都是矩形，则这个几何体的体积是________________cm 3.（2）某几何体的三视图如图所示, 则其表面积为 .【当堂检测】班级：姓名：1.已知正方体的外接球的体积是323π，则这个正方体的棱长是（）A.324B.332C.334D.3222. 一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( )A.(433π+B.(43π+C. (832π+D.(836π+3. 已知圆锥的侧面展开图是一个半径为2的半圆，求其体积.课后巩固案班级：姓名：完成时间：30分钟1.若圆锥的侧面展开图是圆心角为120o 、半径为l 的扇形,则这个圆锥的表面积与侧面积的比是（ ）A.3∶2B.2∶1C.4∶3D.5∶32.如图，一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则其体积是（ ）. A.423 B.433C.36 D.833.某简单几何体的三视图如图所示，其正视图、侧视图、俯视图的面积分别是1，2，4，则这个几何体的体积为 .4. （2013天津）已知一个正方体的所有顶点在一个球面上. 若球的体积为92π, 则正方体的棱长为 .5. 如图有一个外表为圆柱形的容器，其内部表面圆柱内接四棱柱1AC ，其底面是正方形，已知该四棱柱的底面边长为52cm ，圆柱的侧面积为2100cm π，求该容器的容积.俯视图主视图左视图1. 一几何体的三视图如图所示，则该几何体的体积为（）A．2009π+B．20018π+C．1409π+D．14018π+2.一个四棱锥的侧棱长都相等，底面是正方形，其正（主）视图如图所示,则该四棱锥侧面积和体积分别是A.45,8B.8 45,3C.84(51),3+ D.8,83.某几何体的三视图如图所示，则该几何体的体积是 .参考答案 课前自测 1.D 2.C 3.A 4.C 5.297【典例13【变式1】（1）124；（2）92π. 【典例2】表面积为16π+；体积为243π+.【变式2】（1）A ：（2）6. 【典例3】（1）C ；（2）16. 【变式3】（1）32；（2）3π. 【当堂检测】 1.C 2.D.1.C2.B3. 4 35.250π1.A2.B3.16(1)π-。