高中数学简单几何图形与表面积公式

高中数学学考公式大全高中数学学考常用公式及结论必修1：一、集合1、含义与表示：集合中元素具有确定性、互异性和无序性。

集合可以分为有限集和无限集。

集合可以用列举法、描述法和图示法表示。

2、集合间的关系：若对于任意的x∈A，都有x∈B，则称A是B的子集，记作A⊆B。

若A是B的子集，且在B中至少存在一个元素不属于A，则A是B的真子集，记作A⊂B。

若A⊆B且B⊆A，则A=B。

3.元素与集合的关系：属于∈，不属于∉，空集为∅。

4、集合的运算：并集由属于集合A或属于集合B的元素组成的集合叫并集，记为A∪B；交集由集合A和集合B中的公共元素组成的集合叫交集，记为A∩B；补集在全集U中，由所有不属于集合A的元素组成的集合叫补集，记为A'或C。

5．集合{a1,a2,…,an}的子集个数共有2^n个；真子集有2^n–1个；非空子集有2^n–1个。

6.常用数集：自然数集N，正整数集N*，整数集Z，有理数集Q，实数集R。

二、函数的奇偶性1、定义：若对于任意的x∈定义域，有f(–x) =–f(x)，则称函数f为奇函数；若对于任意的x∈定义域，有f(–x) =f(x)，则称函数f为偶函数。

2、性质：（1）奇函数的图象关于原点成中心对称图形；（2）偶函数的图象关于y轴成轴对称图形；（3）如果一个函数的图象关于原点对称，那么这个函数是奇函数；（4）如果一个函数的图象关于y轴对称，那么这个函数是偶函数．三、函数的单调性1、定义：对于定义域为D的函数f(x)，若任意的x1,x2∈D，且x1f(x2)时，称f(x)为减函数。

2、复合函数的单调性：同增异减。

四、二次函数y=ax2+bx+c（a≠0）的性质1、顶点坐标公式：顶点坐标为(-b/2a,f(-b/2a))，对称轴为x=-b/2a，最大（小）值为f(-b/2a)。

2、二次函数的解析式的三种形式：一般式f(x)=ax2+bx+c(a≠0)；顶点式f(x)=a(x-h)2+k(a≠0)；两根式f(x)=a(x-x1)(x-x2)(a≠0)。

高中数学几何公式大全在高中数学中，几何学是一门重要的数学分支。

几何学研究的是空间中的图形和形状的性质、变换以及其关系。

几何学的公式是解决几何问题的基础，本文将为您介绍一些高中数学几何公式。

1.平面几何公式1.1.面积公式-矩形面积公式：面积=长×宽-正方形面积公式：面积=边长×边长-三角形面积公式：面积=（底边长×高）/2-任意多边形面积公式：如果已知多边形所有顶点的坐标，可以使用行列式的方法计算面积。

1.2.周长公式-矩形周长公式：周长=2×(长+宽)-正方形周长公式：周长=4×边长-三角形周长公式：周长=边1+边2+边3-任意多边形周长公式：周长=边1+边2+...+边n1.3.直角三角形公式-勾股定理：a²+b²=c²，其中a、b为直角边，c为斜边。

- 正弦定理：a/sinA=b/sinB=c/sinC，其中a、b、c为三角形边长，A、B、C为对应的角度。

- 余弦定理：c²=a²+b²-2ab*cosC，其中a、b、c为三角形边长，C为对边的角度。

2.立体几何公式2.1.体积公式-立方体体积公式：体积=边长³-球体体积公式：体积=(4/3)πr³，其中r为球的半径-圆柱体体积公式：体积=πr²h，其中r为底面半径，h为高度-锥体体积公式：体积=(1/3)πr²h，其中r为底面半径，h为高度2.2.表面积公式-立方体表面积公式：表面积=6边长²-球体表面积公式：表面积=4πr²- 圆柱体表面积公式：表面积=2πrh+2πr²，其中r为底面半径，h为高度- 锥体表面积公式：表面积=πrl+πr²，其中r为底面半径，l为斜高以上只是高中数学几何公式的一部分，还有许多其他公式未在此列出。

掌握这些公式可以帮助高中生更好地解决几何问题，提高几何学习的效果。

高中数学公式大全立体几何与空间向量高中数学公式大全：立体几何与空间向量一、立体几何立体几何是数学中研究三维空间中的几何图形及其性质的分支，对于高中生来说，常见的立体几何包括了体积、表面积等方面的内容。

下面是一些常用的立体几何公式：1. 立方体体积公式立方体是一种边长相等的六个正方形围成的立体。

其体积公式为：V = 边长³。

2. 正方体体积公式正方体是一种六个面都是正方形的立体。

其体积公式为：V = 底面积 ×高。

3. 长方体体积公式长方体是一种六个面都是矩形的立体。

其体积公式为：V = 长 ×宽×高。

4. 圆柱体积公式圆柱体是一种底面为圆形的立体。

其体积公式为：V = π × 半径² ×高。

5. 圆锥体积公式圆锥体是一种底面为圆形，顶点和底面中心连线垂直于底面的立体。

其体积公式为：V = 1/3 × π × 半径² ×高。

6. 球体积公式球体是一种所有点到球心的距离都相等的立体。

其体积公式为：V= 4/3 × π × 半径³。

7. 棱柱表面积公式棱柱是一种顶面和底面是平行的多边形，侧面是平行四边形的立体。

其表面积公式为：S = 底面积 + 侧面积。

8. 棱锥表面积公式棱锥是一种底面为多边形，侧面是由底面上的点和顶点连线形成的三角形的立体。

其表面积公式为：S = 底面积 + 侧面积。

二、空间向量空间向量是指具有大小和方向的箭头，可以表示空间中的位移、速度、加速度等物理量。

在高中数学中，空间向量常用于解决线性相关、平面垂直、平面平行等问题。

下面是一些常用的空间向量公式：1. 两点之间的距离公式设空间中的两点为A(x₁, y₁, z₁)和B(x₂, y₂, z₂)，则两点之间的距离公式为：AB = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)。

高中数学立体几何知识点总结一 、空间几何体 （一） 空间几何体的类型1 多面体：由若干个平面多边形围成的几何体。

围成多面体的各个多边形叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点。

2 旋转体：把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。

其中，这条直线称为旋转体的轴。

（二） 几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。

棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体性质：Ⅰ、侧面都是平行四边形，且各侧棱互相平行且相等； Ⅱ、两底面是全等多边形且互相平行； Ⅲ、平行于底面的截面和底面全等；棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形1.3 棱柱的面积和体积公式ch S =直棱柱侧（c 是底周长，h 是高）S 直棱柱表面 = c ·h+ 2S 底 V 棱柱 = S 底 ·h2 、棱锥的结构特征2.1 棱锥的定义（1） 棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

（2）正棱锥：如果有一个棱锥的底面是正多边形，并且顶点在底面的投影是底面的中心，这样的棱锥叫做正棱锥。

2.2 正棱锥的结构特征Ⅰ、 平行于底面的截面是与底面相似的正多边形，相似比等于顶点到截面的距离与顶点到底面的距离之比；它们面积的比等于截得的棱锥的高与原棱锥的高的平方比；截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比；Ⅱ、 正棱锥的各侧棱相等，各侧面是全等的等腰三角形； 正棱锥侧面积：1'2S ch =正棱椎（c 为底周长，'h 为斜高） 体积：13V Sh =棱椎（S 为底面积，h 为高） 正四面体：对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。

以下是一些常见的高中数学中使用的体积和面积公式的大全：
平面图形的面积公式：
矩形的面积：$A = l \times w$，其中$l$ 为矩形的长度，$w$ 为矩形的宽度。

正方形的面积：$A = s^2$，其中$s$ 为正方形的边长。

三角形的面积（海伦公式）：$A = \sqrt{s(s-a)(s-b)(s-c)}$，其中$s$ 为半周长，$a$、$b$、$c$ 为三角形的边长。

任意形状的多边形的面积：可以使用分割成三角形或梯形等简单形状的方法计算。

立体图形的体积公式：
直方体的体积：$V = l \times w \times h$，其中$l$、$w$、$h$ 分别为直方体的长度、宽度和高度。

正方体的体积：$V = s^3$，其中$s$ 为正方体的边长。

圆柱体的体积：$V = \pi r^2 h$，其中$r$ 为圆柱体的底面半径，$h$ 为圆柱体的高度。

圆锥体的体积：$V = \frac{1}{3} \pi r^2 h$，其中$r$ 为圆锥体的底面半径，$h$ 为圆锥体的高度。

球体的体积：$V = \frac{4}{3} \pi r^3$，其中$r$ 为球体的半径。

这些公式只是一些常见的示例，实际上数学中还有很多其他的体积和面积公式，具体取决于不同的几何图形和问题。

记住在使用这些公式时，确保使用正确的单位和适当的数值代入。

高中数学必修2知识点总结归纳整理高中数学必修二空间几何体1.1 空间几何体的结构棱柱棱柱是由两个平行的底面和若干个四边形侧面组成的几何体。

底面多边形的边数不同，可以分为三棱柱、四棱柱、五棱柱等。

棱柱可以用各顶点的字母表示，例如五棱柱ABCDE或用对角线的端点字母表示，例如ABCDE。

棱柱的几何特征是：两底面是对应边平行的全等多边形；侧面和对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形。

棱锥棱锥是由一个多边形底面和若干个三角形侧面组成的几何体。

底面多边形的边数不同，可以分为三棱锥、四棱锥、五棱锥等。

棱锥可以用各顶点的字母表示，例如五棱锥P-ABCDE。

棱锥的几何特征是：侧面和对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。

棱台棱台是由一个平行于底面的平面截取棱锥而成的几何体。

底面多边形的边数不同，可以分为三棱台、四棱台、五棱台等。

棱台可以用各顶点的字母表示，例如四棱台ABCD-A'B'C'D'。

棱台的几何特征是：上下底面是相似的平行多边形；侧面是梯形；侧棱交于原棱锥的顶点。

圆柱圆柱是由一个矩形的一边所在的直线为轴旋转，其余三边旋转所成的曲面所围成的几何体。

圆柱的几何特征是：底面是全等的圆；母线与轴平行；轴与底面圆的半径垂直；侧面展开图是一个矩形。

圆锥圆锥是由直角三角形的一条直角边为旋转轴，旋转一周所成的曲面所围成的几何体。

圆锥的几何特征是：底面是一个圆；母线交于圆锥的顶点；侧面展开图是一个扇形。

圆台圆台是由一个平行于圆锥底面的平面截取圆锥而成的几何体。

圆台的几何特征是：上下底面是两个圆；侧面母线交于原圆锥的顶点；侧面展开图是一个弓形。

球体球体是由半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体。

球体的几何特征是：球的截面是圆；球面上任意一点到球心的距离等于半径。

1.2 空间几何体的三视图和直观图1.中心投影与平行投影中心投影是指把光由一点向外散射形成的投影。

高中数学立体几何笔记
一、几何体的基本概念
1、几何体：所谓几何体就是具有体积和表面积的平面图形组合而成的物体。

2、六面体：六面体是指拥有六个相等的面的几何体，例如正方体、立方体等。

六面
体的中心角都是90度，每一个角的夹角都是120度。

4、多面体：多面体指拥有三个以上的不同大小的平面图形组合而成的物体，例如棱柱、棱台等。

二、立体几何公式
1、体积：体积是指容器内部物质所占用的空间，以立方厘米为单位。

体积公式一般
主要有三角形和正多面体两种，推导时要根据物体的实际状态进行计算。

2、表面积：表面积指物体表面覆盖的地方，以平方厘米为单位，其公式也有很多种，也要根据物体实际的状态来推导出合理的公式。

3、代数公式：在计算立体几何中，有一些特殊的概念和计算方式，其中包括体积、
表面积、角度、体积系数等，熟练掌握其公式可以帮助学生理解立体几何，并能更加准确
的计算出几何图形的真实体积、表面积等物理参数。

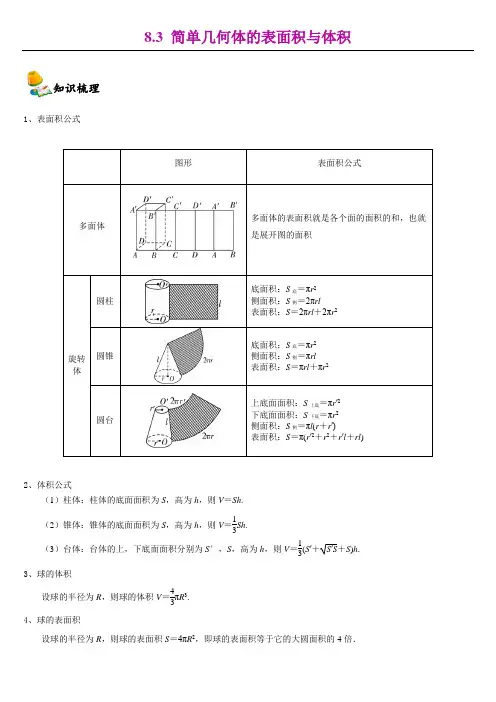
棱柱、棱锥、棱台的表面积和体积高中数学　1.了解棱柱、棱锥、棱台的表面积与体积的计算公式.2.理解并掌握侧面展开图与几何体的表面积之间的关系，并能利用计算公式求几何体的表面积与体积．导语　在初中我们学习了特殊的棱柱——正方体、长方体的体积公式及其表面积的求法，那么对于一个一般的棱柱或棱锥、棱台，它们的体积及表面积又如何来计算呢？一、棱柱、棱锥、棱台的侧面积和表面积问题　我们知道，空间几何体的表面积是围成多面体的各个面的面积之和，长方体、三棱锥、棱台的展开图是什么样子的？提示　知识梳理　多面体的表面积就是围成多面体各个面的面积的和．棱柱、棱锥、棱台的表面积就是围成它们各个面的面积的和．例1　已知正三棱台(由正三棱锥截得的三棱台)的上、下底面边长分别为3 cm 和6 cm ，高为 cm ，求此正三棱台的表面积．32解　如图所示，画出正三棱台ABC －A 1B 1C 1，其中O 1，O 为正三棱台上、下底面的中心，D ，D 1分别为BC ，B 1C 1的中点，则OO 1为正三棱台的高，DD 1为侧面梯形BCC 1B 1的高，四边形ODD 1O 1为直角梯形，所以DD 1＝＝＝，所OO 21＋(OD －O 1D 1)2(32)2＋(3－32)23以此三棱台的表面积S 表＝S 侧＋S 底＝3××(3＋6)×＋×32＋×62＝ (cm 2)．12334349934反思感悟　求解正棱台的表面积时注意棱台的四个基本量：底面边长、高、斜高、侧棱，并注意两个直角梯形的应用(1)高、侧棱、上、下底面多边形的中心与顶点连线所成的直角梯形．(2)高、斜高、上、下底面边心距所成的直角梯形．跟踪训练1　已知棱长均为5，底面为正方形的四棱锥S －ABCD 如图所示，求它的侧面积、表面积．解　∵四棱锥S －ABCD 的各棱长均为5，∴各侧面都是全等的正三角形．设E 为AB 的中点，连接SE (图略)，则SE ⊥AB ，∴S 侧＝4S △SAB ＝4×AB ×SE ＝2×5×＝25，S表＝S 侧＋S 底1252－(52)23＝25＋25＝25(＋1)．33二、棱柱、棱锥、棱台的体积知识梳理　几何体体积说明棱柱V 棱柱＝ShS 为棱柱的底面积，h 为棱柱的高棱锥V 棱锥＝Sh 13S 为棱锥的底面积，h 为棱锥的高棱台V 棱台＝(S ′＋＋S )h13S ′S S ′，S 分别为棱台的上、下底面面积，h 为棱台的高例2　(1)已知高为3的三棱柱ABC －A 1B 1C 1的底面是边长为1的正三角形，如图所示，则三棱锥B 1－ABC 的体积为( )A. B.1412C. D.3634答案　D解析　设三棱锥B 1－ABC 的高为h ，则＝S △ABC h ＝××3＝.1B ABCV 锥－△△13133434(2)正四棱台两底面边长分别为20 cm 和10 cm ，侧面面积为780 cm 2.求其体积．解　正四棱台的大致图形如图所示，其中A 1B 1＝10 cm ，AB ＝20cm ，取A 1B 1的中点E 1，AB 的中点E ，则E1E 为斜高．设O 1，O 分别是上、下底面的中心，则四边形EOO 1E 1为直角梯形．∵S 侧＝4××(10＋20)×EE 1＝780(cm 2)，12∴EE 1＝13 cm.在直角梯形EOO 1E 1中，O 1E 1＝A 1B 1＝5 cm ，OE ＝AB ＝10 cm ，1212∴O 1O ＝＝12(cm)．132－(10－5)2故该正四棱台的体积为V ＝×12×(102＋202＋10×20)＝2 800(cm 3)．13反思感悟　求解正棱台的体积时，注意棱台的五个基本量(上、下底面边长、高、斜高、侧棱)．常用两种解题思路：一是把基本量转化到直角梯形中解决问题；二是把正棱台还原成正棱锥．利用正棱锥的有关知识来解决问题．跟踪训练2　如图，已知正方体ABCD －A 1B 1C 1D 1的棱长为1，则四棱锥A 1－BB 1D 1D 的体积为________．答案　13解析　由题意可知四棱锥A 1－BB 1D 1D 的底面是矩形，边长为1和，四棱锥的高为2A 1C 1＝，1222则四棱锥A 1－BB 1D 1D 的体积为V ＝×1××＝.1322213三、简单组合体的表面积与体积例3　现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P －A 1B 1C 1D 1，下部的形状是正四棱柱ABCD －A 1B 1C 1D 1(如图所示)，并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍，若AB ＝6 m ，PO 1＝2 m ，则仓库的容积是多少？解　由PO 1＝2 m ，知O 1O ＝4PO 1＝8 m.因为A 1B 1＝AB ＝6 m ，所以正四棱锥P －A 1B 1C 1D 1的体积V 锥＝·A 1B ·PO 1＝×62×2＝24 (m 3)，正四棱柱132113ABCD －A 1B 1C 1D 1的体积V 柱＝AB 2·O 1O ＝62×8＝288 (m 3)，所以仓库的容积V ＝V 锥＋V 柱＝24＋288＝312 (m 3)，故仓库的容积是312 m 3.反思感悟　求组合体的表面积和体积，首先应弄清它的组成，其表面有哪些底面和侧面，各个面应该怎样求，然后再根据公式求出各面的面积，最后再相加或相减．求体积时也要先弄清组成，求出各简单几何体的体积，然后再相加或相减．跟踪训练3　如图，在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，截去三棱锥A 1－ABD ，求剩余的几何体A 1B 1C 1D 1－DBC 的表面积和体积．解　由图可知△A 1BD 是边长为a 的等边三角形，其面积为a 2，232故所求几何体A 1B 1C 1D 1－DBC 的表面积S ＝＋3S △1A BDS △DBC ＋3＝a 2＋3××a 2＋3a 2＝a 2.1111A B C D S △△△32123＋92几何体A 1B 1C 1D 1－DBC 的体积V ＝－＝a 3－××a ×a ×a1111ABCD A B C D V －△△△1A ABDV 锥－△△1312＝a 3.561．知识清单：(1)棱柱、棱锥、棱台的侧面积和表面积．(2)棱柱、棱锥、棱台的体积．(3)组合体的表面积与体积．(4)棱柱、棱锥、棱台体积公式之间的关系．2．方法归纳：等体积法、割补法．3．常见误区：平面图形与立体图形的切换不清楚．1．若长方体的长、宽、高分别为3 cm,4 cm,5 cm ，则长方体的体积为( )A ．27 cm 3 B ．60 cm 3 C ．64 cm 3 D ．125 cm 3答案　B解析　V 长方体＝3×4×5＝60(cm 3)．2.如图所示，在正方体ABCD －A 1B 1C 1D 1中，四棱锥S －ABCD 的体积占正方体体积的( )A.B.1213C. D ．不确定14答案　B解析　令正方体棱长为a ，则V 正方体＝a 3，V S －ABCD ＝×a 2×a ＝a 3，1313∴V 四棱锥S －ABCD ＝V 正方体．133．已知正四棱锥，其底面边长为8，侧棱长为，则正四棱锥的侧面积为( )41A ．48 B ．64 C ．80 D ．120答案　C4．棱台的上、下底面面积分别是2,4，高为3，则棱台的体积为________．答案　6＋22解析　V 棱台＝×(2＋4＋)×3132×4＝×3×(6＋2)132＝6＋2.2课时对点练1．正方体的表面积为96，则正方体的体积为( )A ．48 B ．64 C ．16 D ．966答案　B2．已知一直棱柱底面为正方形，它的底面边长为2，体对角线长为4，则这个棱柱的表面积是( )A ．8 B ．16 2C ．8＋12 D ．8＋1622答案　D3．一个棱柱和一个棱锥的高相等，底面积之比为2∶3，则棱柱与棱锥的体积之比为( )A. B ．2 C. D ．31213答案　B解析　设棱柱的高为h ，底面积为S ，则棱锥的高为h ，底面积为S ，故二者的体积之比为32＝＝＝2.V 1V 2Sh13×32Sh214.如图，ABC －A ′B ′C ′是体积为1的三棱柱，则四棱锥C －AA ′B ′B 的体积是( )A. B.1312C. D.2334答案　C解析　∵V 三棱锥C －A ′B ′C ′＝V 三棱柱ABC －A ′B ′C ′＝，1313∴V 四棱锥C －AA ′B ′B ＝1－＝.13235．正四棱柱的侧棱长为5，它的体对角线的长为，则这个棱柱的表面积是( )43A ．15 B ．60 2C ．78 D ．602答案　C解析　如图所示，正四棱柱的侧棱长为AA 1＝5，对角线长为BD 1＝，则(AB )4322＋52＝43，解得AB ＝3，所以这个棱柱的表面积为2×3×3＋4×5×3＝78.6．(多选)用平行于棱锥底面的平面去截棱锥，得到上、下两部分几何体且上下两部分的高之比为1∶2，则关于上下两几何体的说法正确的是( )A ．侧面积之比为1∶4 B ．侧面积之比为1∶8C ．体积之比为1∶27 D ．体积之比为1∶26答案　BD解析　依题意，上部分为小棱锥，下部分为棱台，所以小棱锥与原棱锥的底面边长之比为1∶3，高之比为1∶3，所以小棱锥与原棱锥的侧面积之比为1∶9，体积之比为1∶27，即小棱锥与棱台的侧面积之比为1∶8，体积之比为1∶26.7．正三棱柱ABC －A 1B 1C 1的底面边长为2，侧棱长为，D 为BC 的中点，则三棱锥3A －B 1DC 1的体积为______．答案　1解析　∵正三棱柱ABC －A 1B 1C 1的底面边长为2，侧棱长为，D 为BC 的中点，3∴底面B 1DC 1的面积为×2×＝.1233三棱锥A －B 1DC 1的高就是底面正三角形的高.3三棱锥A －B 1DC 1的体积为××＝1.13338．一个正四棱台，其上、下底面均为正方形，边长分别为8 cm 和18cm ，侧棱长为13cm ，则其表面积为______ cm 2.答案　1 012解析　易知正四棱台侧面为等腰梯形，其高为＝12，所以正四棱台的表面积132－52S ＝4××(8＋18)×12＋82＋182＝1 012(cm 2)．129．现有一个底面是菱形的直四棱柱，它的体对角线长为9和15，高是5，求该直四棱柱的侧面积、表面积．解　如图，设底面对角线AC ＝a ，BD ＝b ，交点为O ，体对角线A 1C ＝15，B 1D ＝9，∴a 2＋52＝152，b 2＋52＝92，∴a 2＝200，b 2＝56.∵该直四棱柱的底面是菱形，∴AB 2＝2＋2＝＝＝64，(AC 2)(BD 2)a 2＋b 24200＋564∴AB ＝8.∴直四棱柱的侧面积S 侧＝4×8×5＝160.直四棱柱的底面积S 底＝AC ·BD ＝20.127直四棱柱的表面积S 表＝160＋2×20＝160＋40.7710.如图，正六棱锥被过棱锥高PO 的中点O ′且平行于底面的平面所截，得到正六棱台OO ′和较小的棱锥PO ′.(1)求大棱锥、小棱锥、棱台的侧面面积之比；(2)若大棱锥PO 的侧棱长为12 cm ，小棱锥的底面边长为4 cm ，求截得的棱台的侧面面积和表面积．解　(1)由题意知S 小棱锥侧∶S 大棱锥侧＝1∶4，则S 大棱锥侧∶S 小棱锥侧∶S 棱台侧＝4∶1∶3.(2)如图所示，∵小棱锥的底面边长为4 cm ，∴大棱锥的底面边长为8 cm ，又PA ＝12 cm ，∴A 1A ＝6 cm.又梯形ABB 1A 1的高h ′＝62－22＝4(cm)，2∴S 棱台侧＝6××4＝144(cm 2)，4＋8222∴S 棱台表＝S 棱台侧＋S 上底＋S 下底＝144＋24＋96＝(144＋120)(cm 2)．2332311.如图，已知正六棱柱的最大对角面的面积为1 m 2，互相平行的两个侧面的距离为1 m ，则这个六棱柱的体积为( )A. m 3B. m 333434C ．1 m 3D. m 312答案　B解析　设正六棱柱的底面边长为am ，高为hm ，则2ah ＝1，a ＝1，解得3a ＝，h ＝，所以六棱柱的体积V ＝×2×6×＝(m 3)．333234(33)323412．侧面都是等腰直角三角形的正三棱锥，底面边长为a 时，该三棱锥的表面积是( )A.a 2 B.a 2 C.a 2 D.a 23＋34343＋326＋34答案　A解析　如图，PA ，PB ，PC两两垂直且PA ＝PB ＝PC ，△ABC 为等边三角形，AB ＝a ，∴PA ＝PB ＝PC ＝a ，22∴表面积为×a 2＋×2×3＝a 2＋a 2＝a 2.3412(22a)34343＋3413．如图，三棱台ABC －A 1B 1C 1中，A 1B 1∶AB ＝1∶2，则三棱锥A 1－ABC ，A 1－B 1C 1B ，A 1－C 1BC 的体积之比为( )A ．1∶1∶1B ．2∶1∶1C ．4∶2∶1D ．4∶1∶2答案　D解析　设三棱台的高为h ，则由题可知三棱锥A 1－ABC 的体积V 1＝×h ×S △ABC ，三棱锥13A 1－B 1C 1B 的体积V 2＝×h ×＝×h ××S △ABC ，三棱锥A 1－C 1BC 的体积13111A B C S △1314V 3＝2V 2，所以三棱锥A 1－ABC ，A 1－B 1C 1B ，A 1－C 1BC 的体积之比为4∶1∶2.14.已知正方体ABCD －A 1B 1C 1D 1的棱长为1，除面ABCD 外，该正方体其余各面的中心分别为点E ，F ，G ，H ，M (如图)，则四棱锥M －EFGH 的体积为________．答案　112解析　连接AD 1，CD 1，B 1A ，B 1C ，AC (图略)，∵E ，H 分别为AD 1，CD 1的中点，∴EH ∥AC ，EH ＝AC .12∵F ，G 分别为B 1A ，B 1C 的中点，∴FG ∥AC ，FG ＝AC ，12∴EH ∥FG ，EH ＝FG ，∴四边形EHGF 为平行四边形，又EG ＝HF ，EH ＝HG ，∴四边形EHGF 为正方形．又四棱锥M －EFGH 的高为，12∴四棱锥M －EFGH 的体积为×2×＝.13(22)1211215.有一塔形几何体由3个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点．已知最底层正方体的棱长为2，则该塔形几何体的表面积为________．答案　36解析　易知由下向上三个正方体的棱长依次为2，，1，2∴S 表＝2×22＋4×[22＋()2＋12]＝36.2∴该几何体的表面积为36.16．在四棱锥E －ABCD 中，底面ABCD 为梯形，AB ∥CD ，2AB ＝3CD ，M 为AE 的中点，设E －ABCD 的体积为V ，那么三棱锥M －EBC 的体积为多少？解　设点B 到平面EMC 的距离为h 1，点D 到平面EMC 的距离为h 2，连接MD ，因为M 是AE 的中点，所以V M －ABCD ＝V ，所以V E －MBC ＝V －V E －MDC .1212而V E －MBC ＝V B －EMC ，V E －MDC ＝V D －EMC ，所以＝＝.VE －MBC VE －MDC VB －EMC VD －EMC h 1h 2因为B ，D 到平面EMC 的距离即为到平面EAC 的距离，而AB ∥CD ，且2AB ＝3CD ，所以＝.h 1h 232所以V E －MBC ＝V M －EBC ＝V .310。

高中数学基本知识点高中数学基本知识点空间几何体表面积体积公式：1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的]体积:πR2h/3(r为圆锥体低圆半径,h 为其高,3、a-边长,S=6a2,V=a34、长方体a-长,b-宽,c-高S=2(ab+ac+bc)V=abc5、棱柱S-h-高V=Sh6、棱锥S-h-高V=Sh/37、S1和S2-上、下h-高V=h[S1+S2+(S1S2)^1/2]/38、S1-上底面积,S2-下底面积,S0-中h-高,V=h(S1+S2+4S0)/69、圆柱r-底半径,h-高,C—底面周长S底—底面积,S侧—,S表—表面积C=2πrS底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h10、空心圆柱R-外圆半径,r-内圆半径h-高V=πh(R^2-r^2)11、r-底半径h-高V=πr^2h/312、r-上底半径,R-下底半径,h-高V=πh(R2+Rr+r2)/313、球r-半径d-直径V=4/3πr^3=πd^3/614、球缺h-球缺高,r-球半径,a-球缺底半径V=πh(3a2+h2)/6=πh2(3r-h)/315、球台r1和r2-球台上、下底半径h-高V=πh[3(r12+r22)+h2]/616、圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr2=π2Dd2/417、桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D2+d2)/12,(母线是圆弧形,圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15(母线是抛物线形)高考数学知识点总结高考数学知识点：参数方程一、坐标系与参数方程：1、坐标系是解析几何的基础。

在坐标系中，可以用有序实数组确定点的位置，进而用方程刻画几何图形。

为便于用代数的方法刻画几何图形或描述自然现象，需要建立不同的坐标系。

高中数学必修2知识点总结立体几何初步特殊几何体表面积公式（c 为底面周长，h 为高，'h 为斜高，l 为母线）chS =直棱柱侧面积'21ch S =正棱锥侧面积 ')(2121h c c S +=正棱台侧面积rhS π2=圆柱侧()l r r S +=π2圆柱表 rlSπ=圆锥侧面积()l r r S +=π圆锥表l R r S π)(+=圆台侧面积()22R Rl rl r S +++=π圆台表柱体、锥体、台体的体积公式V Sh=柱 13V Sh =锥'1()3V S S h =台2V Sh r h π==圆柱 h r V 231π=圆锥'2211()()33V S S h r rR R hπ=+=++圆台（4）球体的表面积和体积公式：V 球=343R π ； S 球面=24R π第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系 12 三个公理：（1符号表示为A ∈LB ∈L => L α A ∈α B ∈α公理1作用：判断直线是否在平面内.（2符号表示为：A 、B 、C 三点不共线 => 有且只有一个平面α，使A ∈α、B ∈α、C ∈α。

公理2作用：确定一个平面的依据。

（3公理1 异面直线： 不同在任何一个平面内，没有公共点。

符号表示为：设a 、b 、c 是三条直线a ∥bc ∥bLA ²α C ²B²A ² α =>a ∥c强调：公理4实质上是说平行具有传递性，在平面、空间这个性质都适用。

公理4作用：判断空间两条直线平行的依据。

4 注意点：① a'与b'所成的角的大小只由a 、b 的相互位置来确定，与O 的选择无关，为了简便，点O 一般取在两直线中的一条上； ② 两条异面直线所成的角θ∈(0， )；③ 当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作a ⊥b ； ④ 两条直线互相垂直，有共面垂直与异面垂直两种情形；⑤ 计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。

简单几何体的表面积与体积【第一课时】【教学目标】1．了解柱体、锥体、台体的侧面展开图，掌握柱体、柱、锥、台的体积2．能利用柱体、锥体、台体的体积公式求体积，理解柱体、锥体、台体的体积之间的关系【教学重难点】1．柱、锥、台的表面积2．锥体、台体的表面积的求法【教学过程】一、问题导入预习教材内容，思考以下问题：1．棱柱、棱锥、棱台的表面积如何计算？2．圆柱、圆锥、圆台的侧面展开图分别是什么？3．圆柱、圆锥、圆台的侧面积公式是什么？4．柱体、锥体、台体的体积公式分别是什么？5．圆柱、圆锥、圆台的侧面积公式、体积公式之间分别有怎样的关系？二、新知探究柱、锥、台的表面积例1：（1）若圆锥的正视图是正三角形，则它的侧面积是底面积的（）A.2倍B．3 倍C．2 倍D．5 倍（2）已知正方体的8 个顶点中，有 4 个为侧面是等边三角形的三棱锥的顶点，则这个三棱锥与正方体的表面积之比为（）A．1∶ 2B．1∶3C．2∶ 2D．3∶6（3）已知某圆台的一个底面周长是另一个底面周长的 3 倍，母线长为 3 ，圆台的侧面积为84π，则该圆台较小底面的半径为（）A．7B．6C．5D．3【解析】（1）设圆锥的底面半径为r，母线长为l，则由题意可知，l＝2r，于是S侧＝πr·2r＝2πr2，S底＝πr2，可知选 C.（2）棱锥B′­ACD′为适合条件的棱锥，四个面为全等的等边三角形，设正方体的棱长为1，则B′C＝2，S△B′AC＝3 2.三棱锥的表面积S锥＝4×32＝23，又正方体的表面积S正＝6.因此S锥∶S正＝23∶6＝1∶ 3.（3）设圆台较小底面的半径为r，则另一底面的半径为3r.由S侧＝3π（r＋3r）＝84π，解得r＝7.【答案】（1）C（2）B（3）A[规律方法]空间几何体表面积的求法技巧（1）多面体的表面积是各个面的面积之和．（2）组合体的表面积应注意重合部分的处理．（3）圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展开为平面图形计算，而表面积是侧面积与底面圆的面积之和．柱、锥、台的体积例2：如图所示，正方体ABCD­A1B1C1D1的棱长为a，过顶点B，D，A1截下一个三棱锥．（1）求剩余部分的体积；（2）求三棱锥A­A1BD的体积及高．【解】（1）V三棱锥A1­ABD＝13S△ABD·A1A＝13×1 2·AB·AD·A1A＝16a3.故剩余部分的体积V＝V正方体－V三棱锥A1­ABD＝a3－16a3＝56a3.（2）V三棱锥A­A1BD＝V三棱锥A1­ABD＝1 6a 3.设三棱锥A­A1BD的高为h，则V三棱锥A­A1BD＝13·S△A1BD·h＝13×12×32（2a）2h＝36a2h，故36a2h＝16a3，解得h＝3 3a.[规律方法]求几何体体积的常用方法（1）公式法：直接代入公式求解．（2）等积法：例如四面体的任何一个面都可以作为底面，只需选用底面积和高都易求的形式即可．（3）补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，棱台补成棱锥等．（4）分割法：将几何体分割成易求解的几部分，分别求体积．[提醒]求几何体的体积时，要注意利用好几何体的轴截面（尤其为圆柱、圆锥时），准确求出几何体的高和底面积．组合体的表面积和体积例3：如图在底面半径为2，母线长为 4 的圆锥中内接一个高为3的圆柱，求圆柱的表面积．【解】设圆锥的底面半径为 R ，圆柱的底面半径为 r ，表面积为 S . 则 R ＝OC ＝2，AC ＝4， AO ＝42－22＝2 3. 如图所示，易知△AEB ∽△AOC ，所以AE AO ＝EB OC ，即323＝r 2，所以 r ＝1，S 底＝2πr 2＝2π，S 侧＝2πr ·h ＝23π. 所以 S ＝S 底＋S 侧＝2π＋23π ＝（2＋23）π.1．[变问法]本例中的条件不变，求圆柱的体积与圆锥的体积之比． 解：由例题解析可知：圆柱的底面半径为 r ＝1，高 h ＝3，所以圆柱的体积 V 1＝πr 2h ＝π×12×3＝3π.圆锥的体积 V 2＝13π×22×23＝833π.所以圆柱与圆锥的体积比为 3∶8.2．[变问法]本例中的条件不变，求图中圆台的表面积与体积．解：由例题解析可知：圆台的上底面半径 r ＝1，下底面半径 R ＝2，高 h ＝3，母线 l ＝2，所以圆台的表面积 S ＝π（r 2＋R 2＋r ·l ＋Rl ）＝π（12＋22＋1×2＋2×2）＝11π.圆台的体积 V ＝13π（r 2＋rR ＋R 2）h ＝13π（12＋2＋22）×3＝733π. 3．[变条件、变问法]本例中的“高为3”改为“高为 h ”，试求圆柱侧面积的最大值．解：设圆锥的底面半径为 R ，圆柱的底面半径为 r ，则R＝OC＝2，AC＝4，AO＝42－22＝2 3.如图所示易知△AEB∽△AOC，所以AEAO ＝EBOC，即23－h23＝r2，所以h＝23－3r，S圆柱侧＝2πrh＝2πr（23－3r）＝－23πr2＋43πr，所以当r＝1，h＝3时，圆柱的侧面积最大，其最大值为23π.[规律方法]求组合体的表面积与体积的步骤（1）分析结构特征：弄清组合体的组成形式，找准有关简单几何体的关键量．（2）设计计算方法：根据组成形式，设计计算方法，特别要注意“拼接面”面积的处理，利用“切割”“补形”的方法求体积．（3）计算求值：根据设计的计算方法求值．【课堂总结】1．棱柱、棱锥、棱台的表面积多面体的表面积就是围成多面体各个面的面积的和．棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和．2．棱柱、棱锥、棱台的体积（1）V棱柱＝Sh；（2）V棱锥＝13Sh；V棱台＝13h（S′＋SS′＋S），其中S′，S分别是棱台的上、下底面面积，h为棱台的高．3．圆柱、圆锥、圆台的表面积和体积名称图形公式圆柱底面积：S底＝πr2侧面积：S侧＝2πrl表面积：S＝2πrl＋2πr2体积：V＝πr2l[名师点拨]1．柱体、锥体、台体的体积（1）柱体：柱体的底面面积为S ，高为h ，则V ＝Sh .（2）锥体：锥体的底面面积为S ，高为h ，则V ＝13Sh . （3）台体：台体的上、下底面面积分别为S ′、S ，高为h ，则V ＝13()S ′＋SS ′＋S h .2．圆柱、圆锥、圆台的侧面积公式之间的关系S 圆柱侧＝2πrl ――→r ′＝r S 圆台侧＝π（r ′＋r ）l ――→r ′＝0S 圆锥侧＝πrl . 3．柱体、锥体、台体的体积公式之间的关系V 柱体＝Sh ――→S ′＝S V 台体＝13（S ′＋S ′S ＋S ）h ――→S ′＝0V 锥体＝13Sh .【课堂检测】1．已知某长方体同一顶点上的三条棱长分别为1，2，3，则该长方体的表面积为（ ）A ．22B ．20C ．10D ．11解析：选A.所求长方体的表面积S ＝2×（1×2）＋2×（1×3）＋2×（2×3）＝22.2．正三棱锥的高为3，侧棱长为23，则这个正三棱锥的体积为（ ）A.274B.94C.2734D.934解析：选D.由题意可得底面正三角形的边长为3，所以V ＝13×34×32×3＝934.故选D.3．已知圆台的上、下底面的面积之比为9∶25，那么它的中截面截得的上、下两台体的侧面积之比是________．解析：圆台的上、下底面半径之比为3∶5，设上、下底面半径为3x ，5x ，则中截面半径为4x ，设上台体的母线长为l ，则下台体的母线长也为l ，上台体侧面积S 1＝π（3x ＋4x ）l ＝7πxl ，下台体侧面积S 2＝π（4x ＋5x ）l ＝9πxl ，所以S 1∶S 2＝7∶9.答案：7∶9 4.如图，三棱台ABC A 1B 1C 1中，AB ∶A 1B 1＝1∶2，求三棱锥A 1ABC ，三棱锥B A 1B 1C ，三棱锥CA 1B 1C 1的体积之比．解：设棱台的高为h ，S △ABC ＝S ，则S △A 1B 1C 1＝4S .所以VA 1ABC ＝13S △ABC ·h ＝13Sh ，VC A 1B 1C 1＝13S △A 1B 1C 1·h ＝43Sh .又V 台＝13h （S ＋4S ＋2S ）＝73Sh ， 所以VB A 1B 1C ＝V 台－VA 1ABC －VCA 1B 1C 1＝73Sh －Sh 3－4Sh 3＝23Sh ， 所以体积比为1∶2∶4.【第二课时】 【教学目标】1．记准球的表面积和体积公式，会计算球的表面积和体积 2．能解决与球有关的组合体的计算问题【教学重难点】1．球的表面积与体积 2．与球有关的组合体【教学过程】一、问题导入预习教材内容，思考以下问题：1．球的表面积公式是什么？2．球的体积公式什么？二、新知探究球的表面积与体积例1：（1）已知球的体积是32π3，则此球的表面积是（）A．12πB．16πC.16π3 D.64π3（2）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径，若该几何体的体积是28π3，则它的表面积是（）A．17π B．18πC．20π D．28π【解析】（1）设球的半径为R，则由已知得V＝43πR3＝32π3，解得R＝2.所以球的表面积S＝4πR2＝16π.（2）由三视图可得此几何体为一个球切割掉18后剩下的几何体，设球的半径为r，故78×43πr3＝283π，所以r＝2，表面积S＝78×4πr2＋34πr2＝17π，选A.【答案】（1）B（2）A[归纳反思]球的体积与表面积的求法及注意事项（1）要求球的体积或表面积，必须知道半径R或者通过条件能求出半径R，然后代入体积或表面积公式求解．（2）半径和球心是球的最关键要素，把握住了这两点，计算球的表面积或体积的相关题目也就易如反掌了．球的截面问题例2：如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器厚度，则球的体积为（）A.500π3cm3 B.866π3cm3C.1 372π3cm3 D.2 048π3cm3【解析】如图，作出球的一个截面，则MC＝8－6＝2（cm），BM＝12AB＝12×8＝4（cm）．设球的半径为R cm，则R2＝OM2＋MB2＝（R－2）2＋42，所以R＝5，所以V球＝43π×53＝5003π （cm3）．【答案】A[规律方法]球的截面问题的解题技巧（1）有关球的截面问题，常画出过球心的截面圆，将问题转化为平面中圆的问题．（2）解题时要注意借助球半径R，截面圆半径r，球心到截面的距离d构成的直角三角形，即R2＝d2＋r2.与球有关的切、接问题角度一球的外切正方体问题例3：将棱长为 2 的正方体木块削成一个体积最大的球，则该球的体积为（）A.4π3B.2π3C.3π2D.π6【解析】由题意知，此球是正方体的内切球，根据其几何特征知，此球的直径与正方体的棱长是相等的，故可得球的直径为 2，故半径为 1，其体积是43×π×13＝4π3.【答案】A角度二球的内接长方体问题例4：一个长方体的各个顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为 1，2，3，则此球的表面积为________．【解析】长方体外接球直径长等于长方体体对角线长，即 2R ＝12＋22＋32＝14，所以球的表面积 S ＝4πR 2＝14π. 【答案】14π角度三球的内接正四面体问题例5：若棱长为 a 的正四面体的各个顶点都在半径为 R 的球面上，求球的表面积．【解】把正四面体放在正方体中，设正方体棱长为 x ，则 a ＝2x ，由题意2R ＝3x ＝3×2a 2＝62a ，所以 S 球＝4πR 2＝32πa 2.角度四球的内接圆锥问题例6：球的一个内接圆锥满足：球心到该圆锥底面的距离是球半径的一半，则该圆锥的体积和此球体积的比值为________．【解析】①当圆锥顶点与底面在球心两侧时，如图所示，设球半径为 r ，则球心到该圆锥底面的距离是r 2，于是圆锥的底面半径为 r 2－⎝ ⎛⎭⎪⎫r 22＝3r 2，高为3r 2.该圆锥的体积为 13 ×π×⎝ ⎛⎭⎪⎫3r 22 ×3r 2＝38πr 3，球体积为43 πr 3，所以11 / 13该圆锥的体积和此球体积的比值为38πr 343πr 3＝932. ②同理，当圆锥顶点与底面在球心同侧时，该圆锥的体积和此球体积的比值为332.【答案】932或332角度五球的内接直棱柱问题例7：设三棱柱的侧棱垂直于底面，所有棱的长都为 a ，顶点都在一个球面上，则该球的表面积为（ ）A ．πa 2B.73πa 2C.113πa 2 D ．5πa 2【解析】由题意知，该三棱柱为正三棱柱，且侧棱与底面边长相等，均为 a ．如图，P 为三棱柱上底面的中心，O 为球心，易知 AP＝23×32a ＝33a ，OP ＝12a ，所以球的半径 R ＝ OA 满足R 2＝⎝ ⎛⎭⎪⎫33a 2＋⎝ ⎛⎭⎪⎫12a 2＝712a 2，故 S 球＝4πR 2＝73πa 2. 【答案】B[规律方法]（1）正方体的内切球球与正方体的六个面都相切，称球为正方体的内切球，此时球的半径为 r 1＝a 2，过在一个平面上的四个切点作截面如图（1）． （2）长方体的外接球长方体的八个顶点都在球面上，称球为长方体的外接球，根据球的定义可知，长方体的体对角线是球的直径，若长方体过同一顶点的三条棱长为 a ，b ，c ，过球心作长方体的对角线，则球的半径为 r 2＝12 a 2＋b 2＋c 2，如图（2）．12 / 13（3）正四面体的外接球正四面体的棱长 a 与外接球半径 R 的关系为：2R ＝62a .【课堂总结】1．球的表面积设球的半径为R ，则球的表面积S ＝4πR 2．2．球的体积设球的半径为R ，则球的体积V ＝43πR 3．[名师点拨]对球的体积和表面积的几点认识（1）从公式看，球的表面积和体积的大小，只与球的半径相关，给定R 都有唯一确定的S 和V 与之对应，故表面积和体积是关于R 的函数．（2）由于球的表面不能展开成平面，所以，球的表面积公式的推导与前面所学的多面体与旋转体的表面积公式的推导方法是不一样的．（3）球的表面积恰好是球的大圆（过球心的平面截球面所得的圆）面积的4倍．【课堂检测】1．直径为 6 的球的表面积和体积分别是（ ）A ．36π，144πB ．36π，36πC ．144π，36πD ．144π，144π解析：选 B ．球的半径为 3，表面积 S ＝4π·32＝36π，体积 V ＝43π·33＝36π.2．一个正方体的表面积与一个球的表面积相等，那么它们的体积比是（ ） A.6π6 B.π2C.2π2D.3π2π解析：选 A ．设正方体棱长为 a ，球半径为 R ，由 6a 2＝4πR 2 得a R ＝2π3，所以V 1V 2＝a 343πR 3＝34π⎝ ⎛⎭⎪⎫2π33＝6π6. 3．若两球的体积之和是 12π，经过两球球心的截面圆周长之和为 6π，则两球的半径之差为（ ）A ．1B ．213 / 13C ．3D ．4解析：选 A ．设两球的半径分别为 R ，r （R >r ），则由题意得⎩⎪⎨⎪⎧4π3R 3＋4π3r 3＝12π，2πR ＋2πr ＝6π，解得⎩⎨⎧R ＝2，r ＝1.故 R －r ＝1. 4．已知棱长为 2 的正方体的体积与球 O 的体积相等，则球 O 的半径为________．解析：设球 O 的半径为 r ，则43πr 3＝23，解得 r ＝36π. 答案：36π5．已知过球面上 A ，B ，C 三点的截面和球心的距离为球半径的一半，且 AB ＝BC ＝CA ＝2，求球的表面积．解：设截面圆心为O ′，球心为 O ，连接 O ′A ，OA ，OO ′，设球的半径为 R .因为O ′A ＝23×32×2＝233.在 Rt △O ′OA 中，OA 2＝O ′A 2＋O ′O 2，所以 R 2＝⎝ ⎛⎭⎪⎫2332＋14R 2， 所以 R ＝43，所以 S 球＝4πR 2＝649π.。

高中数学的几何体表面积和体积公式是哪些高中数学的几何体表面积和体积公式1、圆柱体：表面积：2πRr+2πRh体积：πR2h(R为圆柱体上下底圆半径，h为圆柱体高)2、圆锥体：表面积：πR2+πR[(h2+R2)的平方根]体积：πR2h/3(r为圆锥体低圆半径，h为其高)3、正方体：表面积：S=6a2,体积：V=a3(a-边长)4、长方体：表面积：S=2(ab+ac+bc)体积：V=abc(a-长，b-宽，c-高)5、棱柱：体积：V=Sh(S-底面积，h-高)6、棱锥：体积：V=Sh/3(S-底面积，h-高)7、棱台：V=h[S1+S2+(S1S2)^1/2]/3(S1上底面积，S2下底面积，h-高)8、拟柱体：V=h(S1+S2+4S0)/6(S1-上底面积，S2-下底面积，S0-中截面积，h-高)9、圆柱：S底=πr2，S侧=Ch，S表=Ch+2S底，V=S底h=πr2h(r-底半径，h-高，C—底面周长，S底—底面积，S侧—侧面积，S表—表面积)10、空心圆柱：V=πh(R^2-r^2)(R-外圆半径，r-内圆半径，h-高)11、直圆锥：V=πr^2h/3(r-底半径，h-高)12、圆台：V=πh(R2+Rr+r2)/3(r-上底半径，R-下底半径，h-高)13、球：V=4/3πr^3=πd^3/6(r-半径，d-直径)14、球缺：V=πh(3a2+h2)/6=πh2(3r-h)/3(h-球缺高，r-球半径，a-球缺底半径)15、球台：V=πh[3(r12+r22)+h2]/6(r1球台上底半径，r2-球台下底半径，h-高)16、圆环体：V=2π2Rr2=π2Dd2/4(R-环体半径，D-环体直径，r-环体截面半径，d-环体截面直径)数学基础差的学生如何提高数学成绩基础薄弱的同学提高数学成绩的方法数学基础打牢，是个非常重要的事，很多及格成绩不到的同学，基本是连计算和公式都不是很过关。

对于这一类学生有以下几点建议。

简单几何体的表面积与体积考纲解读 1.结合三视图求几何体的表面积与体积；2.利用几何体的线面关系求表面积和体积；3.求常见组合体的表面积或体积．[基础梳理]1．多面体的表面积与侧面积多面体的各个面都是平面，则多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．2．旋转体的表面积与侧面积名称侧面积 表面积 圆柱(底面半径r ，母线长l ) 2πrl 2πr (l ＋r ) 圆锥(底面半径r ，母线长l ) πrl πr (l ＋r ) 圆台(上、下底面半径r 1，r 2，母线长l )π(r 1＋r 2)lπ(r 1＋r 2)l ＋π(r 21＋r 22) 球(半径为R )4πR 23.空间几何体的体积(h 为高，S 为下底面积，S ′为上底面积) (1)V 柱体＝Sh .特别地，V 圆柱＝πr 2h (r 为底面半径)． (2)V 锥体＝13Sh .特别地，V 圆锥＝13πr 2h (r 为底面半径)．(3)V 台体＝13h (S ＋SS ′＋S ′)．特别地，V 圆台＝13πh (r 2＋rr ′＋r ′2)(r ，r ′分别为上、下底面半径)．(4)V 球＝43πR 3(球半径是R )．[三基自测]1．正六棱柱的高为6，底面边长为4，则它的表面积为( ) A ．48(3＋3) B ．48(3＋23) C ．24(6＋2) D ．144答案：A2．如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为________．答案：1∶473．一直角三角形的三边长分别为6 cm,8 cm,10 cm ，绕斜边旋转一周所得几何体的表面积为________．答案：3365π cm 24．(必修2·1.3A 组改编)球内接正方体的棱长为1，则球的表面积为________． 答案：3π5．(2017·高考全国卷Ⅰ改编)所有棱长都为2的三棱锥的体积为________． 答案：223考点一 几何体的表面积与侧面积|易错突破[例1] (1)(2018·九江模拟)如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的表面积为( )A ．6＋42＋23B ．8＋42C ．6＋6 2D ．6＋22＋43(2)某品牌香水瓶的三视图如图(单位：cm)，则该几何体的表面积为( )A.⎝⎛⎭⎫95－π2cm 2 B.⎝⎛⎭⎫94－π2cm 2 C.⎝⎛⎭⎫94＋π2cm 2 D.⎝⎛⎭⎫95＋π2cm 2 (3)一个几何体的三视图如图所示，则该几何体的表面积为________．[解析] (1)直观图是四棱锥P ABCD ，如图所示，S △P AB ＝S △P AD ＝S △PDC ＝12×2×2＝2，S △PBC ＝12×22×22×sin 60°＝23，S 四边形ABCD ＝22×2＝42，故此棱锥的表面积为6＋42＋23，故选A.(2)该几何体的上下为长方体，中间为圆柱． S 表面积＝S 下长方体＋S 上长方体＋S 圆柱侧－2S 圆柱底＝2×4×4＋4×4×2＋2×3×3＋4×3×1＋2π×12×1－2×π⎝⎛⎭⎫122＝94＋π2(cm 2)． (3)由三视图可知，该几何体是一个长方体内挖去一个圆柱体，如图所示．长方体的长、宽、高分别为4,3,1，表面积为4×3×2＋3×1×2＋4×1×2＝38， 圆柱的底面圆直径为2，母线长为1， 侧面积为2π×1＝2π，圆柱的两个底面面积和为2×π×12＝2π. 故该几何体的表面积为38＋2π－2π＝38. [答案] (1)A (2)C (3)38 [易错提醒]1．以三视图为载体的几何体的表面积或侧面积问题，要分清三视图中的量是否为各表面计算面积所用的量．2．几何体切、割后的图形的表面，不一定是减少，甚至可能增加．3．组合体的表面积，要注意衔接部分分散在哪个面中来计算．[纠错训练]1．已知某斜三棱柱的三视图如图所示，求该斜三棱柱的表面积．解析：由题意知，斜三棱柱的直观图如图中ABC A 1B 1C 1所示．易知正方体的棱长为2.斜三棱柱的两个底面积的和为2S △ABC ＝2×12×AB ×AC ＝2，侧面ABB 1A 1的面积S 侧面ABB 1A 1＝2×1＝2，侧面ACC 1A 1为矩形，S 侧面ACC 1A 1＝AA 1·AC ＝25，侧面BCC 1B 1是边长为5的菱形，连接CB 1、BC 1，易得CB 1＝23，BC 1＝22，且CB 1⊥BC 1，所以S 侧面BCC 1B 1＝12CB 1·BC 1＝12×23×22＝26，所以斜三棱柱ABC A 1B 1C 1的表面积为4＋2(5＋6)．2．(2016·高考全国卷Ⅰ)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，求它的表面积．解析：该几何体是一个球体挖掉18剩下的部分，如图所示，依题意得78×43πR 3＝28π3，解得R ＝2，所以该几何体的表面积为4π×22×78＋34π×22＝17π.考点二 空间几何体的体积|方法突破[例2] (1)(2017·高考全国卷Ⅱ)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )A ．90πB ．63πC ．42πD ．36π(2)正三棱柱ABC A 1B 1C 1的底面边长为2，侧棱长为3，D 为BC 中点，则三棱锥C 1B 1DA 的体积为( )A ．3 B.32 C ．1D.32(3)(2017·高考山东卷)由一个长方体和两个14圆柱体构成的几何体的三视图如下，则该几何体的体积为________．[解析] (1)法一：由题意知，该几何体由底面半径为3，高为10的圆柱截去底面半径为3，高为6的圆柱的一半所得，故其体积V ＝π×32×10－12×π×32×6＝63π.法二：依题意，该几何体由底面半径为3，高为10的圆柱截去底面半径为3，高为6的圆柱的一半所得，其体积等价于底面半径为3，高为7的圆柱的体积，所以它的体积V ＝π×32×7＝63π，选择B.(2) 在正△ABC 中，D 为BC 中点， 则有AD ＝32AB ＝3， S △DB 1C 1＝12×2×3＝ 3.又∵平面BB 1C 1C ⊥平面ABC ，AD ⊥BC ，AD ⊂平面ABC ，∴AD ⊥平面BB 1C 1C ，即AD 为三棱锥A B 1DC 1底面上的高．∴VC 1B 1DA ＝VA C 1B 1D ＝13S △DB 1C 1·AD ＝13×3×3＝1.(3)该几何体由一个长、宽、高分别为2,1,1的长方体和两个底面半径为1，高为1的四分之一圆柱体构成，∴V ＝2×1×1＋2×14×π×12×1＝2＋π2.[答案] (1)B (2)C (3)2＋π2[方法提升]求几何体的体积的方法 方法解读适合题型 直接法对于规则几何体，直接利用公式计算即可．若已知三视图求体积，应注意三视图中的垂直关系在几何体中的位置，确定几何体中的线面垂直等关系，进而利用公式求解 规则 几何体割补法当一个几何体的形状不规则时，常通过分割或者补形的手段将此几何体变为一个或几个规则的、体积易求的几何体，然后再计算．经常考虑将三棱锥还原为三棱柱或长方体，将三棱柱还原为平行六面体，将台体还原为锥体不规则 几何体 等积转换法 利用三棱锥的“等积性”可以把任一个面作为三棱锥的底面．求体积时，可选择“容易计算”的方式来计算三棱锥[跟踪训练]1．(2018·大连双基检测)如图，在边长为1的正方形网格中用粗线画出了某个多面体的三视图，则该多面体的体积为( )A ．15B ．13C ．12D ．9解析：几何体的直观图如图所示，其中底面ABCD 是一个矩形(其中AB ＝5，BC ＝2)，棱EF ∥底面ABCD ，且EF ＝3，直线EF 到底面ABCD 的距离是3.连接EB ，EC ，则题中的多面体的体积等于四棱锥E ­ABCD 与三棱锥E ­FBC 的体积之和，而四棱锥E ­ABCD 的体积等于13×(5×2)×3＝10，三棱锥E ­FBC 的体积等于13×⎝⎛⎭⎫12×3×3×2＝3，因此题中的多面体的体积等于10＋3＝13，选B.答案：B2．如图所示(单位：cm)，则图中的阴影部分绕AB 所在直线旋转一周所形成的几何体的体积为________．解析：由题图中数据，根据圆台和球的体积公式，得 V圆台＝13×(π×AD 2＋π×AD 2×π×BC 2＋π×BC 2)×AB ＝13×π×(AD 2＋AD ×BC ＋BC 2)×AB＝13×π×(22＋2×5＋52)×4＝52π(cm 3)， V 半球＝43π×AD 3×12＝43π×23×12＝163π(cm 3)，所以旋转所形成几何体的体积V ＝V 圆台－V半球＝52π－163π＝1403π(cm 3)．答案：1403π(cm 3)考点三 有关球的组合体及面积、体积最值问题|思维突破[例3] (1)已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积取最大值时，其高的值为( )A ．33 B.3 C ．2 6D ．23(2)(2017·高考全国卷Ⅰ)已知三棱锥S ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥S ABC 的体积为9，则球O 的表面积为________．(3)正四棱柱ABCD A 1B 1C 1D 1的各顶点都在半径为R 的球面上，则正四棱柱的侧面积有最________值，为________．[解析] (1)设正六棱柱的底面边长为a ，高为h ，则可得a 2＋h 24＝9，即a 2＝9－h 24，那么正六棱柱的体积V ＝⎝⎛⎭⎫6×34a 2×h ＝332(9－h 24)h ＝332(－h 34＋9h )． 令y ＝h 34＋9h ，∴y ′＝－3h 24＋9.令y ′＝0，∴h ＝2 3.易知当h ＝23时，正六棱柱的体积最大，故选D.(2)设球O 的半径为R ，∵SC 为球O 的直径，∴点O 为SC 的中点，连接AO ，OB (图略)，∵SA ＝AC ，SB ＝BC ，∴AO ⊥SC ，BO ⊥SC ，∵平面SCA ⊥平面SCB ，平面SCA ∩平面SCB ＝SC ，∴AO ⊥平面SCB ，∴V SABC ＝V ASBC ＝13×S △SBC×AO ＝13×(12×SC ×OB )×AO ，即9＝13×(12×2R ×R )×R ，解得R ＝3，∴球O 的表面积为S ＝4πR 2＝4π×32＝36π.(3)如图，截面图为长方形ACC 1A 1和其外接圆．球心为EE 1的中点O ， 则R ＝OA .设正四棱柱的侧棱长为b ，底面边长为a ，则AC ＝2a ，AE ＝22a ，OE ＝b2，R 2＝⎝⎛⎭⎫22a 2＋⎝⎛⎭⎫b 22， ∴4R 2＝2a 2＋b 2，则正四棱柱的侧面积： S ＝4ab ＝2·2a ·2b ≤2(a 2＋2b 2)＝42R 2，故侧面积有最大值，为42R 2，当且仅当a ＝2b 时等号成立． [答案] (1)D (2)36π (3)大 42R 2 [思维升华]1．求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形问题，再利用平面几何知识寻找几何中元素间的关系求解．2．解决几何体最值问题的方法 方法解读适合题型基本不等式法根据条件建立两个变量的和或积为定值，然后利用基本不等式求体积的最值(1)求棱长或高为定值的几何体的体积或表面积的最值；(2)求表面积一定的空间几何体的体积最大值和求体积一定的空间几何体的表面积的最小值函数法通过建立相关函数式，将所求的组合体中的最值问题最值问题转化为函数的最值问题求解，此法应用最为广泛几何法 由图形的特殊位置确定最值，如垂直图形位置变化中的最值[跟踪训练](2015·高考全国卷Ⅱ)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π解析：△AOB 的面积为定值，当OC 垂直于平面AOB 时，三棱锥O ABC 的体积取得最大值．由16R 3＝36得R ＝6.从而球O 的表面积S ＝4πR 2＝144π.故选C.答案：C1.[考点二](2017·高考全国卷Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A ．π B.3π4 C.π2D.π4解析：球心到圆柱的底面的距离为圆柱高的12，球的半径为1，则圆柱底面圆的半径r＝1－(12)2＝32，故该圆柱的体积V ＝π×(32)2×1＝3π4，故选B.答案：B2.[考点一](2016·高考全国卷Ⅱ)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A ．20πB ．24πC ．28πD ．32π解析：由三视图知圆锥的高为23，底面半径为2，则圆锥的母线长为4，所以圆锥的侧面积为12×4π×4＝8π.圆柱的底面积为4π，圆柱的侧面积为4×4π＝16π，从而该几何体的表面积为8π＋16π＋4π＝28π，故选C.答案：C3.[考点二](2015·高考全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )A ．14斛B ．22斛C ．36斛D ．66斛解析：设圆锥底面的半径为R 尺，由14×2πR ＝8得R ＝16π，从而米堆的体积V ＝14×13πR 2×5＝16×203π(立方尺)，因此堆放的米约有16×203×1.62×3≈22(斛)．故选B.答案：B4.[考点一、三](2017·高考全国卷Ⅱ)长方体的长、宽、高分别为3,2,1，其顶点都在球O 的球面上，则球O 的表面积为________．解析：依题意得，长方体的体对角线长为32＋22＋12＝14，记长方体的外接球的半径为R ，则有2R ＝14，R ＝142，因此球O 的表面积等于4πR 2＝14π.答案：14π5.[考点一、三](2017·高考全国卷Ⅰ改编)如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O上的点，△DBC ，△ECA ，△F AB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△F AB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，求所得三棱锥体积(单位：cm 3)的最大值．解析：法一：由题意可知，折起后所得三棱锥为正三棱锥，当△ABC 的边长变化时，设△ABC 的边长为a (a >0)cm ，则△ABC 的面积为34a 2，△DBC 的高为5－36a ，则正三棱锥的高为⎝⎛⎭⎫5－36a 2－⎝⎛⎭⎫36a 2＝25－533a ， ∴25－533a >0，∴0<a <53，∴所得三棱锥的体积V ＝13×34a 2×25－533a ＝312×25a 4－533a 5.令t ＝25a 4－533a 5，则t ′＝100a 3－2533a 4，由t ′＝0，得a ＝43，此时所得三棱锥的体积最大，为415 cm 3.法二：如图，连接OD 交BC 于点G ，由题意知，OD ⊥BC .易得OG ＝36BC ，∴OG 的长度与BC 的长度成正比．设OG ＝x ，则BC ＝23x ，DG ＝5－x ，S △ABC ＝23x ·3x ·12＝33x 2，则所得三棱锥的体积V ＝13×33x 2×(5－x )2－x 2＝3x 2×25－10x ＝3×25x 4－10x 5.令f (x )＝25x 4－10x 5，x ∈⎝⎛⎭⎫0，52，则f ′(x )＝100x 3－50x 4，令f ′(x )>0，即x 4－2x 3<0，得0<x <2，则当x ∈⎝⎛⎭⎫0，52时，f (x )≤f (2)＝80，∴V ≤3×80＝415.∴所求三棱锥的体积的最大值为415.。

第五节 空间几何体的表面积和体积【知识点20】空间几何体的表面积一般地，我们可以把多面体展开成平面图形，求出展开图中各个小多边形的面积，然后相加即为多面体的表面积． 1.直棱柱和正棱锥的表面积(1)直棱柱的侧面积①侧棱和底面垂直的棱柱叫做直棱柱．②直棱柱的侧面展开图是矩形，这个矩形的长等于直棱柱的底面周长c ，宽等于直棱柱的高h ，因此，直棱柱的侧面积是S 直棱柱侧＝ch . ③底面为正多边形的直棱柱叫做正棱柱． (2)正棱锥的侧面积①如果一个棱锥的底面是正多边形，并且顶点在底面的正投影是底面中心，那么称这样的棱锥为正棱锥．正棱锥的侧棱长都相等．②棱锥的侧面展开图是由各个侧面组成的，展开图的面积就是棱锥的侧面积．如果正棱锥的底面周长为c ，斜高(即侧面等腰三角形底边上的高)为h ′，它的侧面积是S 正棱锥侧＝12ch ′.2.正棱台的表面积正棱锥被平行于底面的平面所截，截面和底面之间的部分叫做正棱台．与正棱锥的侧面积公式类似，若设正棱台的上、下底面的周长分别为c ′，c ，斜高为h ′，则其侧面积是S 正棱台侧＝12(c ＋c ′)h ′. 3.圆柱、圆锥、圆台的表面积【推导圆柱侧面积及表面积】S 侧＝2πrl ，S 表＝2πr (r ＋l )．【推导圆锥侧面积及表面积】底面周长是2πr ，利用扇形面积公式得 S 侧＝12×2πrl ＝πrl ，S 表＝πr 2＋πrl ＝πr (r ＋l )．【推导圆台侧面积及表面积】由题图知，圆台的侧面展开图是扇环，内弧长等于圆台上底周长，外弧长等于圆台下底周长，则x x ＋l ＝r R ，解得x ＝r R －rl . S 扇环＝S 大扇形－S 小扇形＝12(x ＋l )×2πR －12x ×2πr ＝π[(R －r )x ＋Rl ]＝π(r ＋R )l ，所以S 圆台侧＝π(r ＋R )l ，S 圆台表＝π(r 2＋rl ＋Rl ＋R 2)．【类型一】 求多面体的侧面积和表面积 【例1】正四棱台两底面边长分别为a 和b (a <b )．(1)若侧棱所在直线与上、下底面正方形中心的连线所成的角为45°，求棱台的侧面积；(2)若棱台的侧面积等于两底面面积之和，求它的高．【变式1】已知正四棱台的高是12 cm，两底面边长之差为10 cm，表面积为512 cm2，求底面的边长．【反思】(1)求棱锥、棱台及棱柱的侧面积和表面积的关键是求底面边长，高，斜高，侧棱．求解时要注意直角三角形和梯形的应用．(2)正棱柱、正棱锥、正棱台的所有侧面都全等，因此求侧面积时，可先求一个侧面的面积，然后乘以侧面的个数．(3)棱台是由棱锥所截得到的，因此棱台的侧面积也可由大小棱锥侧面积作差得到．【变式2】已知正四棱锥的侧面积是底面积的2倍，高为3，求它的表面积．【变式3】如图，在正方体ABCD —A1B1C1D1中，三棱锥D1—AB1C的表面积与正方体的表面积的比为________．【思考1】如图，已知正三棱锥S－ABC的侧面积是底面积的2倍，正三棱锥的高SO＝3，求此正三棱锥的表面积．【类型二】与三视图结合综合问题【例2】某四面体的三视图如图所示，该四面体四个面的表面积为 .【变式1】一个四面体的三视图如图所示，则该四面体的表面积是（）A. 2+B. 1C. 1+D.【变式2】如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体各面中直角三角形的个数是A. 2B. 3C. 4D. 5【变式3】已知一个几何体的三视图如图所示（单位:m），其中俯视图为正三角形,则该几m何体的体积为_______3【思考2】某几何体的三视图如图所示，则该几何体的表面积为.【思考3】某三棱锥的三视图如图所示，则该三棱锥的体积为A. 60B. 30C. 20D. 10【变式1】如图是一个几何体的三视图，在该几何体的各个面中，面积最小的面的面积为（）A. 8B. 4C.D.【类型三】求旋转体的表面积【例3】圆台的上、下底面半径分别为10 cm和20 cm.它的侧面展开图扇环的圆心角为180°，那么圆台的表面积是________ cm2.(结果中保留π)【变式1】圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，求圆台较小底面的半径．【反思】(1)求圆柱、圆锥和圆台的侧面积和表面积，只需求出上、下底半径和母线长即可，求半径和母线长时常借助轴截面．(2)解答旋转体的侧面积与表面积问题可先把空间问题转化为平面问题，即在展开图内求母线的长，再进一步代入侧面积公式求出侧面积，进而求出表面积．(3)旋转体的轴截面是化空间问题为平面问题的重要工具，因为在轴截面中集中体现了旋转体的“关键量”之间的关系．在推导这些量之间的关系时要注意比例性质的应用．【变式2】若圆锥的母线长为2 cm，底面圆的周长为2π cm，则圆锥的表面积为________ cm2.【变式3】以圆柱的上底中心为顶点，下底为底作圆锥，假设圆柱的侧面积为6，圆锥的侧面积为5，求圆柱的底面半径．【变式4】若一个圆台的轴截面如图所示，则其侧面积等于______．【变式5】．一个圆柱和一个圆锥的轴截面分别是边长为a 的正方形和正三角形，则它们的表面积之比为________．【类型四】与三视图结合的综合问题【例4】一个几何体的三视图如图所示，其中正视图与侧视图都是斜边长为的直角三角形，俯视图是半径为，圆心角为的扇形，则该几何体的表面积是（ ）A. B. C. D.【变式1】如图是一个封闭几何体的三视图，则该几何体的表面积为（ ）A. 27cm π B. 28cm π C. 29cm π D. 211cm π【类型五】 简单组合体的表面积【例5】牧民居住的蒙古包的形状是一个圆柱与圆锥的组合体，尺寸如图所示(单位：m)，请你帮助算出要搭建这样的一个蒙古包至少需要多少篷布？(精确到0.01 m 2)【反思】 (1)组合体的侧面积和表面积问题，首先要弄清楚它是由哪些简单几何体组成，然后再根据条件求各个简单组合体的基本量，注意方程思想的应用．(2)在实际问题中，常通过计算物体的表面积来研究如何合理地用料，如何节省原材料等，在求解时应结合实际，明确实际物体究竟是哪种几何体，哪些面计算在内，哪些面实际没有． 【变式1】有两个相同的直棱柱，高为2a ，底面三角形的边长分别为3a,4a,5a (a >0)．用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，表面积最小的是一个四棱柱，求a 的取值范围．【变式2】如图所示，△ABC 的三边长分别是AC ＝3，BC ＝4，AB ＝5，作CD ⊥AB ，垂足为点D .以AB 所在直线为轴，将此三角形旋转一周，求所得旋转体的表面积．【方法小结】1．多面体的表面积为围成多面体的各个面的面积之和．棱柱的表面积等于它的侧面积加底面积；棱锥的表面积等于它的侧面积加底面积；棱台的表面积等于它的侧面积加两个底的面积．2．有关旋转体的表面积的计算要充分利用其轴截面，就是说将已知条件尽量归结到轴截面中求解．而对于圆台有时需要将它还原成圆锥，再借助相似的相关知识求解．3．S圆柱表＝2πr(r＋l)；S圆锥表＝πr(r＋l)；S圆台表＝π(r2＋rl＋Rl＋R2)．【思考1】如图(1)所示，已知正方体面对角线长为a，沿阴影面将它切割成两块，拼成如图(2)所示的几何体，那么此几何体的表面积为________．【思考2】一个圆锥的底面半径为2 cm，高为6 cm，在其中有一个高为x cm的内接圆柱．(1)求圆锥的侧面积；(2)当x为何值时，圆柱的侧面积最大？求出最大值．【变式1】已知某圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则该圆台较小底面的半径为________．【知识点21】空间几何体的体积【类型一】柱体、锥体、台体的体积【例1】(1)如图所示，已知三棱柱ABC－A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1－ABC1的体积为____________．(2)现有一个底面直径为20 cm的装有一部分水的圆柱形玻璃杯，水中放着一个底面直径为6 cm，高为20 cm的圆锥形铅锤，铅锤完全浸没在水中．当铅锤从水中取出后，杯里的水将下降________ cm.【反思】(1)常见的求几何体体积的方法①公式法：直接代入公式求解．②等积法：如四面体的任何一个面都可以作为底面，只需选用底面积和高都易求的形式即可．一、柱体、锥体、台体的体积公式1．柱体的体积公式V＝Sh(S为底面面积，h为高)．2．锥体的体积公式V＝13Sh(S为底面面积，h为高)．3．台体的体积公式V＝13(S′＋S′S＋S)h(S′，S为上、下底面面积，h为高)．4．柱体、锥体、台体的体积公式之间的关系V＝Sh V＝13(S′＋S′S＋S)h V＝13Sh.二、球的表面积和体积公式1．球的表面积公式S＝4πR2(R为球的半径)．2．球的体积公式V＝43πR3.三、球体的截面的特点1．球既是中心对称的几何体，又是轴对称的几何体，它的任何截面均为圆．2．利用球半径、截面圆半径、球心到截面的距离构建直角三角形是把空间问题转化为平面问题的主要途径．③分割法：将几何体分割成易求解的几部分，分别求体积．(2)求几何体体积时需注意的问题柱、锥、台体的体积的计算，一般要找出相应的底面和高，要充分利用截面、轴截面，求出所需要的量，最后代入公式计算．【变式1】如图所示，在长方体ABCD－A′B′C′D′中，用截面截下一个棱锥C－A′DD′，求棱锥C－A′DD′的体积与剩余部分的体积之比．【变式2】已知一个三棱台上、下底面分别是边长为20 cm和30 cm的正三角形，侧面是全等的等腰梯形，且侧面面积等于上、下底面面积之和，求棱台的高和体积．【变式3】已知正三棱锥S—ABC，D，E分别为底面边AB，AC的中点，则四棱锥S—BCED 与三棱锥S—ABC的体积之比为________．【变式4】圆柱形容器内盛有高度为6 cm的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球，如图所示．则球的半径是________ cm.【变式5】如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器的厚度，则球的体积为____ cm3.【类型二】球的表面积与体积【例2】（外接球）(1)设长方体的长，宽，高分别为2a，a，a，其顶点都在一个球面上，则该球的表面积为________．(2)求球与它的外切等边圆锥(轴截面是正三角形的圆锥叫等边圆锥)的体积之比．【变式1】一倒置圆锥体的母线长为10 cm，底面半径为6 cm.(1)求圆锥体的高；(2)一球刚好放进该圆锥体中，求这个球的半径以及此时圆锥体剩余的空间．【反思】(1)正方体的内切球球与正方体的六个面都相切，称球为正方体的内切球，此时球的半径为r 1＝a2，过在一个平面上的四个切点作截面如图①. (2)球与正方体的各条棱相切球与正方体的各条棱相切于各棱的中点，过球心作正方体的对角面有r 2＝22a ，如图②. (3)长方体的外接球长方体的八个顶点都在球面上，称球为长方体的外接球，根据球的定义可知，长方体的体对角线是球的直径，若长方体过同一顶点的三条棱长为a ，b ，c ，则过球心作长方体的对角面有球的半径为r 3＝12a 2＋b 2＋c 2，如图③.(4)正方体的外接球正方体棱长a 与外接球半径R 的关系为2R ＝3a . (5)正四面体的外接球正四面体的棱长a 与外接球半径R 的关系为2R ＝62a . 【练习1】长方体共顶点的三个侧面面积分别为3，5，15，则它的外接球表面积为________．【练习2】将棱长为2的正方体木块削成一个体积最大的球，则该球的体积为________．【练习3】设三棱柱的侧棱垂直于底面，所有棱的长都为a ，顶点都在一个球面上，则该球的表面积为________．【练习4】三棱锥P ABC -中， ,,PA PB PC 互相垂直， 1PA PB ==， M 是线段BC上一动点，若直线AM 与平面PBC 所成角的正切的最大值是2，则三棱锥P ABC -的外接球的表面积是（ ）A. 2πB. 4πC. 8πD. 16π【例3】在正三棱锥S −ABC 中，SA =2√7，AB =6，则该三棱锥外接球的直径为( )A. 7B. 8C. 9D. 10【反思】在一个多面体的面找外接圆的圆心，过该圆的圆心，作垂直于该面的垂线，球心O 在垂线上，构造三角形，解三角形。