精选残差分析讲义.
- 格式:ppt
- 大小:622.00 KB
- 文档页数:15

什么是残差分析如何利用残差分析来检验回归模型的适用性残差分析是统计学中一种常用的方法,用于评估回归模型的适用性。
在回归分析中,我们希望通过建立数学模型来描述自变量与因变量之间的关系。
残差分析则是用来检验模型是否能准确地描述实际数据。
残差(residual)是指观测值与回归方程预测值之间的差异。
回归方程可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε,其中Y是因变量,X1、X2、...、Xn是自变量,β0、β1、β2、...、βn是回归系数,ε是误差。
残差计算公式为:残差 = 观测值 - 预测值。
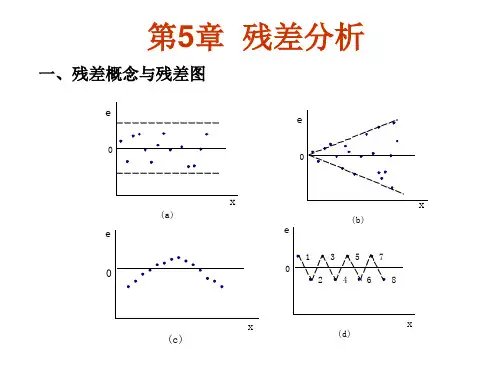
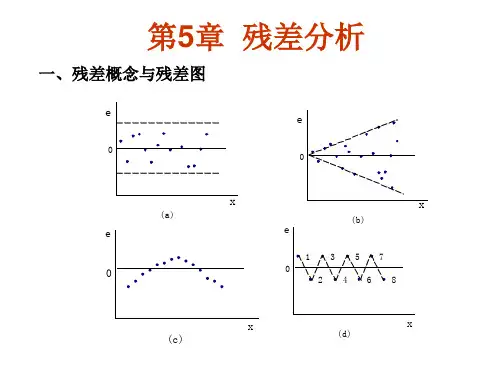
当回归模型适用性良好时,残差应该随机分布在零附近,没有明显的模式或趋势。
接下来,我们将介绍如何利用残差分析来检验回归模型的适用性。
1. 绘制残差图(Residual Plot)残差图是一种展示残差分布的可视化方式。
在横轴上绘制观测值或预测值,纵轴上绘制残差。
如果残差图中的点随机分布在零附近,并且没有明显的模式,则说明回归模型适用性较好。
如果残差图中存在模式或趋势,那么回归模型可能存在问题,需要重新评估模型的可靠性。
2. 检查残差的正态性回归模型通常假设误差项(ε)满足正态分布。
我们可以通过绘制残差的直方图或概率图来检查残差是否服从正态分布。
如果残差近似服从正态分布,则说明回归模型的适用性较好。
3. 检查残差的独立性残差的独立性是指残差之间没有相关性。
我们可以通过绘制残差的自相关图(Autocorrelation Plot)来检验残差是否独立。
如果残差之间没有显示出明显的相关性,则说明回归模型的适用性较好。
4. 检查残差的等方差性等方差性是指残差的方差在自变量的不同取值范围内是恒定的。
我们可以绘制残差的散点图,以观察残差的方差是否与预测值相关。
如果散点图呈现出均匀分布且没有明显的锥形或漏斗形状,则说明回归模型的适用性较好。
总结来说,残差分析是用于检验回归模型适用性的重要方法。





第四节残差分析、预报和控制一、残差分析前面咱们介绍了线性回归方程的成立和查验。
在实际问题中,由于观察人员的粗心或偶然因素的干扰。
常会使咱们所取得的数据不完全靠得住, 即出现异样数据。
有时即便通过相关系数或F查验证明回归方程靠得住,也不能排除数据存在上述问题。
残差分析的目的就在于解决这一问题。
所谓残差是指实际观察值与回归估量值的差,即(2-1-26)显然,有多少对数据,就有多少个残差。
残差分析就是通过残差所提供的信息,分析出数据的靠得住性、周期性或其它干扰。
第一介绍如何检查异样数据。
异样数据是指与其它数据产生的条件有明显不同的数据,因此异样数据的残差会特别的大。
一旦发觉异样数据应及时剔除,用剩余数据从头成立回归方程,以提高回归方程的质量。
发觉异样数据主要从技术上找原因,当技术上无法找到原因时,就得借助于数理统计方式。
由数理统计方式能够证明(2-1-27) 或记为(2-1-28)这说明残差的方差D(e)是x的函数,且二者呈曲线关系。
以回归方程及方程和作图。
见方开泰《实用回归分析》P45图考虑到较小,当n较大时(2-1-29) 现在图中的两条曲线可近似于两条平行直线。
从而有(2-1-30) 或近似地(2-1-31)这表明,当n较大时y i落在图2-1-3的长条形带子中的概率约为95%,只要明白,就可以够取得残差的置信区域。
一般是未知的,通常常利用残差标准差来估量。
可用下式求得(2-1-32) 由此可得残差置信带(2-1-33)对残差在置信带之外的数据都要进行检查,以区别是不是是异样数据,若是是异样数据就要剔除掉。
此刻咱们对例1做残差检查。
由式(2-1-32)残差置信带为,。
计算5个实验点的预报值与残差值(见表2-1-4),并作出残差检查图(见图2-1-4)表2-1-4 例1的残差值图2-1-4 例1的残差图由图2-1-4可见,例1中全数数据的残差都在置信带内,没有异样数据。
除此之外,残差图还能够为咱们提供许多有效信息。



1. 如何做残差分析?残差是指实际观察值与回归估计值的差,即()n i y y e i i i ,,2,1^Λ=-= ,有多少对数据,就有多少个残差。
残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰 。
可以通过Matlab 作残差图来分析残差,比如: 程序如下:x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x];Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';[b,bint,r,rint,stats]=regress(Y,X)rcoplot(r,rint)残差图:-5-4-3-2-11234Residual Case Order PlotR e s i d u a l s Case Number从残差图可以看出数据的残差离零点的远近,当残差的置信区间均包含零点,这说明回归模型能较好的符合原始数据,否则可视为异常点。
2. 剔除异常数据的原则与方法;原则:异常数据是指与其它数据产生的条件有明显不同的数据,因此异常数据的残差会特别的大。
一旦发现异常数据应及时剔除,用剩余数据重新建立回归方程,以提高回归方程的质量 。
发现异常数据主要从技术上找原因,当技术上无法找到原因时,就得借助于数理统计方法。
对残差在置信带以外的数据都要进行检查,以区别是否是异常数据,如果是异常数据就要剔除掉。
方法㈠:⑴对于线性数列,求出所有相邻两数之差,得到一个新的数列,然后统计新数列的众数(就是出现最多的那个)得到线性数列的公差;⑵然后假设第一个数是非异常数字;⑶假设数据不断加公差,看看绝大大多数是不是在原线性数列中,分情况:①若是,则第一个数以及第一个数加公差与原数列相同的元素均为非异常数据,其他则为异常数据;②若不是,则第一个数为异常数列,再假设第2个非异常数据,返回到第⑶步。