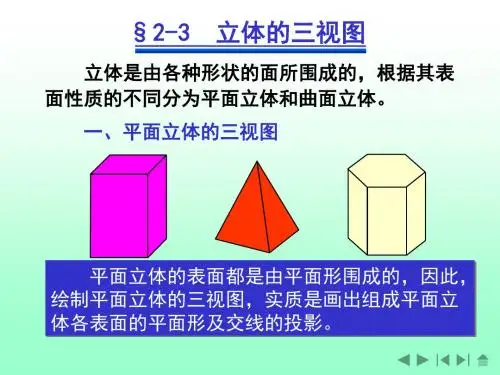
三视图转立体图

曲面立体常见的曲面立体是回转体，回转体是由回转面或回转面与平面围成的立体。

回转面通常由一条直线或曲线绕一固定直线作回转运动而形成的曲面，如图所示。

固定的直线称为轴线，作回转运动的线称为母线，母线在运动过程中所处的任意位置称为素线，母线上任意一点的运动轨迹是圆，常称为纬圆。

(a)圆柱 (b)圆锥 (c)球 (d)圆环回转面的形成绘制回转体的三视图归结为绘制回转体的轮廓线、顶点和曲面转向轮廓线的投影。

转向轮廓线：投射线与曲面的切线转向轮廓线投影：是指切于曲面的各投射线与投影面的交点的集合，也就是这些投射线所组成的投射面（平面或柱面）与投影面的交线，如图所示。

曲面转向轮廓线的投影也是曲面在该投影面上投影可见与不可见的分界线。

1．圆柱1）圆柱的三视图圆柱由圆柱面和两个平面围成。

三视图如图b所示。

圆柱的尺寸注法如图c所示。

（a）立体图（b）三视图（c）尺寸注法圆柱体的三视图及尺寸注意：绘制圆柱等回转体的三视图时应先用细点画线画出立体的轴线、对称中心线。

2）圆柱表面上取点在圆柱面上取点，首先要确定点在圆柱面的哪个部分，然后利用圆柱面投影的积聚性以及点的投影规律，确定圆柱面上点的位置、投影及可见性。

例题：如图a所示，已知圆柱面上M点的正面投影m’和N点的侧面投影n”。

求M点和N点的其余两个投影。

分析：因圆柱轴线垂直于水平投影面，M、N点在圆柱面上，它们的水平投影面投影必在圆上。

由已知条件可知，M点在左前圆柱面上，故m”为可见；N 点在右前圆柱面上，n’为可见。

作图：m’求得m，由m’、m得m”，判别可见性。

n”求得n，由n”、n得m’，判别可见性。

（a）已知条件（b）M点作图（c）N点作图圆柱表面取点3）圆柱表面上取线回转体表面上的线通常是空间曲线，特殊情况下是平面曲线或直线。

步骤：①确定出该线段在立体表面上的特殊点:线段的端点、该线经过立体表面转向轮廓线投影上的点；②在特殊点之间插入一些一般点；③光滑、平顺地连接各点。

怎样将几何的三视图还原为立体几何图形
三视图还原立体几何简单与否因人而异，空间想象力强的人，一眼便能看出是什么样的图形。

我就觉得这种题目还是挺简单的，哈哈。

首先我给你几个最常见的例子。

1.三面都是长方，就是长方体；2.上面看圆，两个侧面看长方，就是圆柱；3.上面看圆，两侧面看三角，就是圆锥；4.上面看多边形，两侧面看三角，就是棱锥；5.上面看多边形，两侧看长方，就是棱柱；6.上面看圆，两侧看梯形，就是圆台；7.三面都是圆，就是球。

其次要注意的是，三视图显示了图形的长宽高，从上方看的图显示了长宽或者直径之类的东西，从侧面看的图显示了长和高，或者宽和高，或者直径和高之类的。

第三要是你空间想象力不强，那么就得多练习。

至于方法，我觉得多锻炼逆向思维能力是最好的。

你可以随便想象出一个立体图形，然后自己给那个图形画三视图，然后再只看你的三视图想象你刚才想的图形，反复练习，多总结，我想你会有启发、收获的。

最后说说三视图的作用。

要是你单看三视图，这个东西高考也不会考，看似没有用，实际上它是很有用的。

它为你以后的立体几何题的分析打下了一定的基础，是一个融入于解题思路中的方法。

综上所述，建议你好好练习三视图。

三视图的投影规律
三视图是一种空间图形的三个视角视图，其中包括正视图、侧视图和俯视图，也称为前视图、侧视图和俯视图。

三视图由三个投影面构成，分别为水平面、竖直面和前平面，而具体的投影规律主要体现在投影面上。

一、正视图的投影规律
1、高度方向上的投影：在投影面上，通过高度方向上的平移，将空间立体图向下平移，直至固定的水平面，投影即为正视图。

2、宽度方向上的投影：将三维图形绕垂直于水平面的轴线旋转，使其旋转到垂直于水平面，投影即为正视图。

3、深度方向上的投影：在投影面上，将空间立体图向前平移，直至固定的投影面，投影即为正视图。

二、侧视图的投影规律
1、高度方向上的投影：同正视图的投影规律一致，都是通过高度方向上的平移，将空间立体图向下平移至水平面，投影即为侧视图。

2、宽度方向上的投影：在投影面上，将三维图形旋转到垂直于竖直面，投影即为侧视图。

3、深度方向上的投影：将三维图形沿垂直于侧视图的轴线顺时针或逆时针旋转，使其旋转到与竖直面平行的水平面上，投影即为侧视图。

三、俯视图的投影规律
1、高度方向上的投影：在投影面上，将空间立体图向下平移至水平面，投影即为俯视图。

2、宽度方向上的投影：将三维图形沿竖直于水平面的轴线逆时针或顺时针旋转，使其旋转到与水平面垂直，投影即为俯视图。

3、深度方向上的投影：同侧视图的投影规律一致，都是将三维图形沿垂直于俯视图的轴线顺时针或逆时针旋转，旋转到与水平面平行的位置，投影即为俯视图。

综上所述，三视图的投影规律主要体现在投影面的平移和旋转上。

通过对三视图的投影规律的了解，可以更好地理解并绘制出三维图形的三视图。

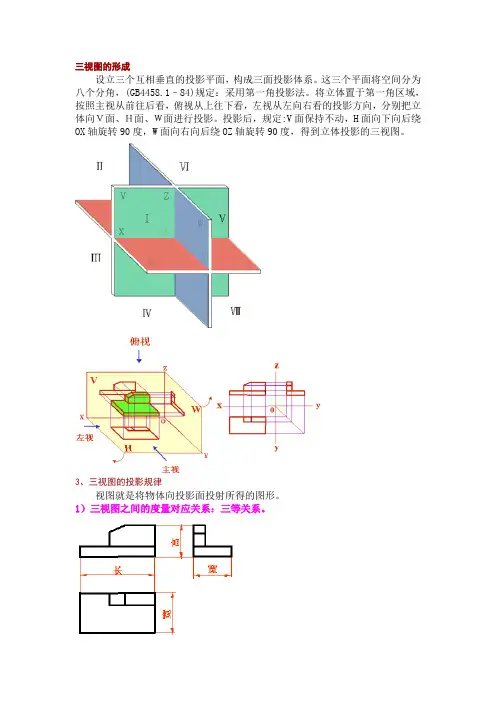
三视图的形成
设立三个互相垂直的投影平面，构成三面投影体系。

这三个平面将空间分为八个分角，(GB4458.1–84)规定：采用第一角投影法。

将立体置于第一角区域，按照主视从前往后看，俯视从上往下看，左视从左向右看的投影方向，分别把立体向Ｖ面、Ｈ面、Ｗ面进行投影。

投影后，规定:V面保持不动，H面向下向后绕OX轴旋转90度，W面向右向后绕OZ轴旋转90度，得到立体投影的三视图。

3、三视图的投影规律
视图就是将物体向投影面投射所得的图形。

1）三视图之间的度量对应关系：三等关系。

2）三视图之间的方位对应关系
主视图反映：上、下、左、右
俯视图反映：前、后、左、右
左视图反映：上、下、前、后。

三视图还原直观图“五步走”石门县第一中学415300陈锦鑫三视图是高中立体几何中的一个重要知识点，也是今后进一步学习机械制图、建筑制图等的必修课，三视图也是近几年高考必考的知识点。

主要题型就是给出几何体的三视图，计算几何体的面积和体积等相关量。

学生丢分的主要原因是不能由三视图还原为几何体，画出相应的直观图。

本文通过一道例题介绍一种将三视图还原成实物图的方法。

如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，将该三视图还原成实物图第一步：根据三视图中三种视图的长与宽，作一个与正视图等长等高，与俯视图等宽的长方体。

例如本例中需要作一个边长为2的正方体ABCD-A’B’C’D’，如图。

第二步:根据三视图中的正视图对长方体切割。

例如本例中由正视图知道，原几何体只能在三棱柱ADD’-BCC’范围内，因此将三棱柱AA’D’-BB’C’部分截掉，如图。

第三步：根据三视图中的侧视图对剩余几何体切割。

例如本例中由侧视图知道，原几何体只能在四棱锥C’-ABCD范围内，因此将三棱锥D’-ADC’部分截掉，如图。

第四步：根据三视图中的俯视图对剩余几何体切割。

，同时结合三种视图需要将例如本例中由俯视图知道，原几何体在底面上的投影为BCD三棱锥C’-ABDC部分截掉，得到三棱锥C’-BCD，如图。

第五步：根据三种视图多边形内部的实线或虚线对剩余几何体切割。

例如本例中正视图、俯视图中均有一条虚线，三视图的虚线表示虚线所在的位置有立体图形的轮廓线,只是在观察者所在的位置看不到。

根据正视图、俯视图中知点E为三棱锥C’-BCD 中BC边的中点，连接ED、EC’，ED、EC’是立体图形的轮廓线，因此我们需要将截掉三棱锥C’-ECD,得到三棱锥C’-BDE即为三视图所对应的实物图。