山东大学 自动控制原理 71描述函数法

词汇第一章自动控制 ( Automatic Control) ：是指在没有人直接参与的条件下，利用控制装置使被控对象的某些物理量（或状态）自动地按照预定的规律去运行。

自动控制系统：将被控对象和控制装置（控制器）按照一定的方式连接起来构成的有机总体。

开环控制 ( open loop control )：开环控制是最简单的一种控制方式。

它的特点是，按照控制信息传递的路径，控制量与被控制量之间只有前向通路而没有反馈通路。

也就是说，控制作用的传递路径不是闭合的，故称为开环。

闭环控制 ( closed loop control) ：凡是将系统的输出量反送至输入端，对系统的控制作用产生直接的影响，都称为闭环控制系统或反馈控制 Feedback Control 系统。

这种自成循环的控制作用，使信息的传递路径形成了一个闭合的环路，故称为闭环。

复合控制 ( compound control ）：是开、闭环控制相结合的一种控制方式。

被控对象：指需要给以控制的机器、设备或生产过程。

被控对象是控制系统的主体，例如火箭、锅炉、机器人、电冰箱等。

控制装置则指对被控对象起控制作用的设备总体，有测量变换部件、放大部件和执行装置。

被控量 (controlled variable ) ：指被控对象中要求保持给定值、要按给定规律变化的物理量。

被控量又称输出量、输出信号。

给定值 (set value ) ：是作用于自动控制系统的输入端并作为控制依据的物理量。

给定值又称输入信号、输入指令、参考输入。

干扰 (disturbance) ：除给定值之外，凡能引起被控量变化的因素，都是干扰。

干扰又称扰动。

第二章数学模型 (mathematical model) ：是描述系统内部物理量（或变量）之间动态关系的数学表达式。

传递函数 ( transfer function) ：线性定常系统在零初始条件下，输出量的拉氏变换与输入量的拉氏变换之比，称为传递函数。

自动控制原理第三版自动控制原理（第三版）第一章引论本章简要介绍了自动控制的基本概念和发展历程，并对自动控制系统的组成和基本原理进行了概述。

通过对自动控制领域的引言，为后续章节的学习提供了基础。

第二章数学模型的建立与分析本章详细介绍了建立自动控制系统数学模型的方法和技巧。

包括对连续和离散系统的建模过程，以及常见系统的数学描述方法。

此外，还对模型的稳定性和性能进行了分析，为后续章节中的控制器设计提供了理论基础。

第三章传递函数本章主要讨论了连续系统的传递函数表示方法，并介绍了常见的传递函数运算技巧。

通过对传递函数的深入研究，为后续章节中的控制器设计和分析提供了工具和方法。

第四章控制系统的时域分析方法本章介绍了控制系统在时域分析中应用的方法和技巧。

包括对单位阶跃响应和单位冲激响应的分析，以及通过阶跃响应法进行系统参数估计的方法。

通过对时域分析的深入学习，可以更好地理解和分析控制系统的动态响应。

第五章控制系统的频域分析方法本章主要介绍了控制系统在频域分析中的应用。

包括对频率响应曲线和波特图的分析，以及使用频域方法进行系统性能评估和控制器设计的技巧。

通过对频域分析的学习，可以更好地理解和优化控制系统的频率特性。

第六章控制系统的稳定性分析本章详细介绍了控制系统的稳定性分析方法和技巧。

包括对闭环系统的稳定性判据和稳定性分析方法的讲解，以及通过根轨迹法和Nyquist稳定性判据进行系统稳定性分析的实例。

通过对稳定性分析方法的学习，可以更好地评估和改善控制系统的稳定性。

第七章比例控制本章主要介绍了比例控制的原理和应用。

包括对比例控制器的基本结构和工作原理的解释，以及比例控制的优缺点和应用领域的说明。

通过对比例控制的学习，可以更好地理解和应用控制系统中的比例控制器。

第八章积分控制本章详细介绍了积分控制的原理和应用。

包括对积分控制器的结构和工作原理进行了解释，以及积分控制的优缺点和应用案例的讲解。

通过对积分控制的学习，可以更好地理解和应用控制系统中的积分控制器。

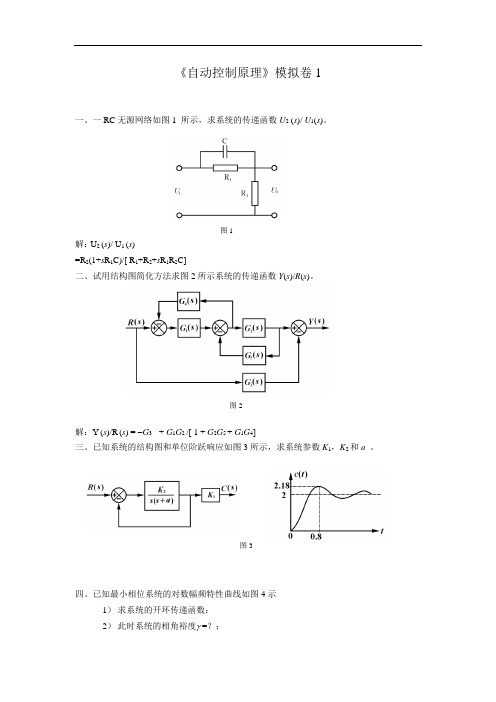
《自动控制原理》模拟卷1一、一RC无源网络如图1 所示，求系统的传递函数U2 (s)/ U1(s)。

解：U2 (s)/ U1 (s)=R2(1+s R1C)/[ R1+R2+s R1R2C]二、试用结构图简化方法求图2所示系统的传递函数Y(s)/R(s)。

解：Y(s)/R(s) = -G3 + G1G2 /[ 1 + G2G5 + G1G4]三、已知系统的结构图和单位阶跃响应如图3所示，求系统参数K1，K2和a。

四、已知最小相位系统的对数幅频特性曲线如图4示1）求系统的开环传递函数；2）此时系统的相角裕度γ=？；图1图2图3五、已知负反馈系统的开环传递函数为)11.0(40)(+=s s s G要求：保持稳态误差不变，且校正后系统的相角裕度γ' ≥ 45︒。

1) 画出原系统的Bode 图，求ωc ，γ 。

2) 确定串联超前校正装置的传递函数；（要有必要的步骤，不用校验） 解：1) ωc = 20 γ = 26.6︒ 2) G c (s ) = 1+0.084s / 1+0.03s图4《自动控制原理》模拟卷2一、一有源网络如图1 所示，求系统的传递函数U c(s)/ U r(s)。

二、已知控制系统如图2所示，求：（1）当K = 0时，确定系统的阻尼系数ζ、无阻尼振荡频率ωn和单位斜坡输入信号作用时系统的稳态误差e ss。

（2）当ζ= 0.707时，试确定系统中的K值和单位斜坡输入时系统的稳态误差。

图1图2三、已知单位负反馈系统的开环传递函数为)2)(1()(++=s s s ks G1）画出系统的开环极坐标图（写出必要的步骤）。

2）用奈氏判据判断使闭环系统稳定时k 的取值范围。

四、已知最小相位系统的对数幅频特性曲线如图3所示1） 求系统的开环传递函数； 2） 此时系统的相角裕度γ =？； 3） 画出系统的对数相频特性曲线。

解：1) G k (s ) = 2.5(1+1/0.5s ) / s 2 (1+1/50s )2) ωc = 5 γ = 78.6︒五、已知负反馈系统的开环传递函数为)11.0(40)(+=s s s G要求：保持稳态误差不变，且校正后系统的相角裕度γ' ≥ 45︒。

自动控制原理（山东大学）知到章节测试答案智慧树2023年最新第一章测试1.下列家用电器哪个属于闭环控制？（）参考答案:冰箱2.下列系统哪个属于闭环控制？（）参考答案:空调3.开环控制方式简单，控制精度高。

参考答案:错4.只要有反馈通道，一定是闭环控制。

参考答案:对5.线性系统一定会满足叠加原理的。

参考答案:对6.满足叠加原理的系统，一定是线性系统。

参考答案:对7.复合控制方式是既有开环控制，又有闭环控制。

参考答案:对8.电枢控制的直流电动机反馈控制系统是属于（）。

参考答案:连续控制系统;线性定常系统;恒值控制系统9.雷达天线控制系统是属于（）。

参考答案:随动控制系统;连续控制系统;线性定常系统10.计算机控制系统是属于（）。

参考答案:离散控制系统第二章测试1.不同的物理系统，可以是同一种环节，同一个物理系统也可能成为不同的环节，这是与描述他们动态特性的微分方程相对应的。

参考答案:对2.常见的典型环节有几种？参考答案:63.在线性定常系统中，系统输出的拉普拉斯变换与输入的拉普拉斯变换之比，称为系统的传递函数。

参考答案:错4.物理系统线性微分方程一般表示形式中，方程左端导数阶次都输入的阶次。

参考答案:高于或等于5.传递函数描述系统本身属性，与输入量的关系是：参考答案:与输入量的大小和类型均有关6.传递函数表示成零极点表达式时，其中的传递系数又叫根轨迹增益。

参考答案:对7.以下描述错误的是：参考答案:零点的位置决定模态的敛散性8.振荡环节中的参数wn称为有限振荡频率。

参考答案:错9.建立控制系统的数学模型有两种基本方法，分别是分析法和实验法。

参考答案:对10.由输入到输出的直接通道传递函数的乘积称为开环传递函数。

参考答案:错第三章测试1.与单位抛物线函数相比，抛物线函数3t^2的幅值是多少？参考答案:62.一阶系统1/(Ts+1)的单位斜坡响应是有差的，稳态时的误差是:参考答案:T3.对于二阶振荡系统，当阻尼比=0.58时，其超调量约等于参考答案:10%4.某二阶系统的开环传递函数为16/(s(0.25s+1))，其自然振荡频率为：参考答案:85.已知某系统的超调量为30%，峰值时间为0.1s，则系统的自然振荡频率为：参考答案:33.656.某系统的开环极点都是位于实轴上，则该系统是非振荡的。

自动控制理论知到章节测试答案智慧树2023年最新山东大学第一章测试1.自动控制系统的工作原理是检测{偏差}，再以{偏差}为控制作用，从而消除偏差。

（）参考答案:对2.自动控制装置由{测量元件}，{比较元件}，调节元件，{执行元件}四部分组成。

（）参考答案:对3.连续系统是指系统中各部分的输入和输出信号都是连续变化的模拟量。

（）参考答案:对4.线性定常系统是用线性常系数微分方程描述的系统。

（）参考答案:对5.给定输入是对系统输出量的要求值。

（）对6.被控量是指被控系统所要控制的物理量。

（）参考答案:对7.被控对象是指被控制的机器，设备和生产过程。

（）参考答案:对8.下列选项中，开环控制系统是指系统的输出量对系统（）。

参考答案:无控制作用9.闭环控制系统是系统的输出量对系统有控制作用。

（）参考答案:对10.开环控制系统的特点是结构简单，无反馈，不能纠正偏差。

闭环控制系统的特点是能自动纠正偏差，需要考虑稳定性问题。

（）对第二章测试1.求图示系统的传递函数（）参考答案:2.下列选项中，求图示无源网络的传递函数G(S)==（）参考答案:3.下列选项中，求图示无源网络的传递函数G(S)==（）参考答案:4.下列选项中，求图示无源网络的传递函数G(S)=（）参考答案:5.用解析法列写线性系统的微分方程有哪些步骤？（）。

参考答案:确定输入输出、根据物理定律列元件各变量的微分方程、消中间变量、标准化6.传递函数与输入和初始条件无关。

（）参考答案:对7.物理性质不同的系统，完全可以有相同的传递函数。

（）参考答案:对8.状态向量是以状态变量为元所组成的向量。

（）参考答案:对9.状态变量是确定系统状态的最少数目的一组变量。

（）参考答案:对10.建立数学模型的基本方法为分析法试验法。

（）参考答案:对第三章测试1.系统稳定，则特征多项式一定满足必要条件＞0。

（）参考答案:对2.偶极子是指两者间的距离比它们的模小一个数量级的一对闭环零、极点。

自动控制原理仿真实验课程山东大学智慧树知到答案2024年绪论单元测试1.本实验课程中所采用的实验工具为MATLAB计算软件。

A:错 B:对答案:B项目一测试1.控制系统数学模型的实验目的是（）。

A:掌握多环节串联连接时整体传递函数的求取方法 B:掌握多环节反馈连接时整体传递函数的求取方法 C:掌握用MATLAB创建各种控制系统模型 D:掌握多环节并联连接时整体传递函数的求取方法答案:ABCD2.运用Matlab创建控制系统数学模型实验中介绍了（）个实验原理。

A:4个 B:2个 C:5个 D:3个答案:C3.Feedback（）与Cloop（）函数中的sign参数表示的意义是不一样的。

（）A:错 B:对答案:A4.用Matlab将传递函数转换为零极点形式的程序代码是（）。

A:num=[1,3,2,1,1]; den=[1,4,3,2,3,2];G1=tf(num1, den1); G=zpk(G1)B:num1=[1,3,2,1,1]; den=[1,4,3,2,3,2];G1=tf(num, den1); G=zpk(G1)C:num1=[1,3,2,1,1]; den1=[1,4,3,2,3,2];G1=tf(num, den); G=zpk(G1)D:num=[1,3,2,1,1]; den=[1,4,3,2,3,2];G1=tf(num, den); G=zpk(G1)答案:D5.用Matlab将传递函数表达式转换成多项式的程序代码是（）。

A:num= [15, 45]; den=conv(conv([1,1],[1,5]),[1,15]); G=tf(num1, den1)B:num= [15, 45]; den=conv(conv([1,1] [1,5]) [1,15]); G=tf(num, den) C:K=15;Z=[-3]; P=[-1;-5;-15]; G1=zpk(Z,P,K); G=tf(G1) D:K=15; Z=[-3]; P=[-1;-5;-15];G=zpk(Z,P,K)答案:AC项目二测试1.典型环节模拟方法及动态特性的实验目的是（）。

2021年自考自动控制原理（一）重点：数学描述方法第二章自动控制系统的数学描述方法（一）学习目的与要求通过本章的学习使学生掌握自动控制系统的三种数学模型（微分方程、传递函数、结构图）的建立方法。

熟练掌握自动控制系统传递函数的求取方法。

（二）课程内容第一节RL，RC或RLC网络及简单电机拖动系统、机械系统的微分方程列写方法。

第二节传递函数概念，传递函数定义及性质，由系统微分方程求传递函数方法，复阻抗法求给定R、L、C一阶或二阶网络的传递函数。

第三节闭环控制系统典型结构框图，系统开环传递函数，利用动态结构图及梅森公式求传递函数。

第四节控制系统的几种常用传递函数。

（三）考核知识点1、掌握RL，RC或RLC网络及简单电机拖动系统、机械系统的微分方程列写方法。

2、重点掌握理解传递函数定义及性质、系统微分方程求传递函数方法，熟练运用复阻抗法求给定R、L、C一阶或二阶网络的传递函数。

3、理解闭环控制系统典型结构框图，系统开环传递函数，能应用动态结构图及梅森公式求传递函数。

4、掌握控制系统的几种常用传递函数。

（四）考核要求1、制系统的微分方程（一般）（1）领会：RL，RC或RLC网络及简单电机拖动系统、机械系统的微分方程列写方法。

2、函数（重点）（1）识记：传递函数概念。

（2）领会：传递函数定义及性质。

（3）简单应用：由系统微分方程求传递函数。

会用复阻抗法求给定R、L、C一阶或二阶网络的传递函数。

3、结构图与梅森公式（一般）（1）识记：结构图的组成，几种典型环节的传递函数。

（2）领会：结构图及等效变换原则，系统开环传递函数。

(3) 简单应用：能应用动态结构图及其等效变换熟练求取输入或干扰作用下系统的闭环传递函数，用梅逊公式法求系统的传递函数4、系统的几种常用传递函数(次重点)（1）领会：控制系统的几类典型的环节。