各种截面回转半径近似值计算图表
- 格式:pdf
- 大小:875.74 KB
- 文档页数:2


回转半径科技名词定义中文名称:回转半径英文名称:radius of gyration其他名称:惯性半径定义:在转动惯量不变的条件下,设想构件的质量集中在某一点,该点到转动轴线的距离。
应用学科:机械工程(一级学科);机构学(二级学科);机构动力学(三级学科)本内容由全国科学技术名词审定委员会审定公布回转半径是一个物理量,虽与动力学中回转半径有相似的数学表达形式,但含义不同。
回转半径是指物体微分质量假设的集中点到转动轴间的距离[1],它的大小等于转动惯量除以总质量后再开平方。
当一力矩作用于一个物体时,物体会呈现应有的旋转运动。
物体对于一个直轴的回转半径,是此物体所有粒子,对于此直轴的均方根距离。
物体对于一个直轴的回转半径,是与对于此直轴的转动惯量和物体的质量有关。
物理上认为,刚体按一定规律分布的质量,在转动中等效于集中在某一点上的一个质点的质量,假设此点离某轴线的垂距为k,刚体对该轴线的转动惯量与该等效质点对此同一轴线的转动惯量相等,即I=mk^2,则k称为该刚体对该轴线的回转半径。
回转半径的大小与截面的形心轴有关。
最小回转半径一般指非对称截面中(如不等边角钢),对两个形心轴的回转半径中的较小者。
这在计算构件的长细比时,如构件的平面内和平面外计算长度相等时,它的长细比就要用最小回转半径计算。
长细比是指杆件的计算长度与杆件截面的回转半径之比。
注意,是杆件的计算长度,计算长度与杆件端部的连接方式有关,如固接、铰接、链接、自由,长细比并不是长边与短边之比。
编辑本段运用长柱子钢筋混凝土偏心受压长柱子承载力计算要考虑到外载作用下,因构件弹塑性变性引起的附加偏心的影响,偏心距增大系数与轴心受压构件的稳定系数,都与长细比有关。
短柱子柱子还由于长细比来分为短柱子,长柱子和细长柱子。
根据这我们来判别柱子类型,在实际中就可以尽量避免使用细长柱。
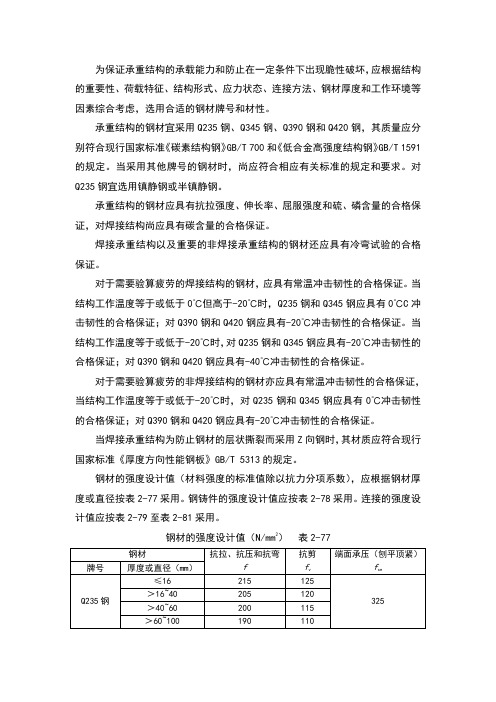
为保证承重结构的承载能力和防止在一定条件下出现脆性破坏,应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑,选用合适的钢材牌号和材性。
承重结构的钢材宜采用Q235钢、Q345钢、Q390钢和Q420钢,其质量应分别符合现行国家标准《碳素结构钢》GB/T 700和《低合金高强度结构钢》GB/T 1591的规定。
当采用其他牌号的钢材时,尚应符合相应有关标准的规定和要求。
对Q235钢宜选用镇静钢或半镇静钢。
承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证,对焊接结构尚应具有碳含量的合格保证。
焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯试验的合格保证。
对于需要验算疲劳的焊接结构的钢材,应具有常温冲击韧性的合格保证。
当结构工作温度等于或低于0℃但高于-20℃时,Q235钢和Q345钢应具有0℃C冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有-20℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-40℃冲击韧性的合格保证。
对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证,当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有0℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当焊接承重结构为防止钢材的层状撕裂而采用Z向钢时,其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。
钢材的强度设计值(材料强度的标准值除以抗力分项系数),应根据钢材厚度或直径按表2-77采用。
钢铸件的强度设计值应按表2-78采用。
连接的强度设计值应按表2-79至表2-81采用。
钢材的强度设计值(N/mm2)表2-77注:表中厚度系指计算点的钢材厚度,对轴心受力构件系指截面中较厚板件的厚度。

2-5 钢结构计算2-5-1 钢结构计算用表为保证承重结构的承载能力和防止在一定条件下出现脆性破坏,应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑,选用合适的钢材牌号和材性。
承重结构的钢材宜采用Q235钢、Q345钢、Q390钢和Q420钢,其质量应分别符合现行国家标准《碳素结构钢》GB/T 700和《低合金高强度结构钢》GB/T 1591的规定。
当采用其他牌号的钢材时,尚应符合相应有关标准的规定和要求。
对Q235钢宜选用镇静钢或半镇静钢。
承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证,对焊接结构尚应具有碳含量的合格保证。
焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯实验的合格保证。
对于需要验算疲劳的焊接结构的钢材,应具有常温冲击韧性的合格保证。
当结构工作温度等于或低于0℃但高于-20℃时,Q235钢和Q345钢应具有0℃C冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有-20℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-40℃冲击韧性的合格保证。
对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证,当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有0℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当焊接承重结构为防止钢材的层状撕裂而采用Z向钢时,其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。
钢材的强度设计值<材料强度的标准值除以抗力分项系数),应根据钢材厚度或直径按表2-77采用。
钢铸件的强度设计值应按表2-78采用。
连接的强度设计值应按表2-79至表2-81采用。
钢材的强度设计值<N/mm2)表2-77注:表中厚度系指计算点的钢材厚度,对轴心受力构件系指截面中较厚板件的厚度。

2-5 钢结构计算2-5-1 钢结构计算用表为保证承重结构的承载能力和防止在一定条件下出现脆性破坏,应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑,选用合适的钢材牌号和材性。
承重结构的钢材宜采用Q235钢、Q345钢、Q390钢和Q420钢,其质量应分别符合现行国家标准《碳素结构钢》GB/T 700和《低合金高强度结构钢》GB/T 1591的规定。
当采用其他牌号的钢材时,尚应符合相应有关标准的规定和要求。
对Q235钢宜选用镇静钢或半镇静钢。
承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证,对焊接结构尚应具有碳含量的合格保证。
焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯试验的合格保证。
对于需要验算疲劳的焊接结构的钢材,应具有常温冲击韧性的合格保证。
当结构工作温度等于或低于0℃但高于-20℃时,Q235钢和Q345钢应具有0℃C冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有-20℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-40℃冲击韧性的合格保证。
对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证,当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有0℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当焊接承重结构为防止钢材的层状撕裂而采用Z向钢时,其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。
钢材的强度设计值(材料强度的标准值除以抗力分项系数),应根据钢材厚度或直径按表2-77采用。
钢铸件的强度设计值应按表2-78采用。
连接的强度设计值应按表2-79至表2-81采用。
钢材的强度设计值(N/mm2)表2-77注:表中厚度系指计算点的钢材厚度,对轴心受力构件系指截面中较厚板件的厚度。

回转半径科技名词定义中文名称:回转半径英文名称:radius of gyration其他名称:惯性半径定义:在转动惯量不变的条件下,设想构件的质量集中在某一点,该点到转动轴线的距离。
应用学科:机械工程(一级学科);机构学(二级学科);机构动力学(三级学科)本内容由全国科学技术名词审定委员会审定公布回转半径是一个物理量,虽与动力学中回转半径有相似的数学表达形式,但含义不同。
回转半径是指物体微分质量假设的集中点到转动轴间的距离[1],它的大小等于转动惯量除以总质量后再开平方。
当一力矩作用于一个物体时,物体会呈现应有的旋转运动。
物体对于一个直轴的回转半径,是此物体所有粒子,对于此直轴的均方根距离。
物体对于一个直轴的回转半径,是与对于此直轴的转动惯量和物体的质量有关。
物理上认为,刚体按一定规律分布的质量,在转动中等效于集中在某一点上的一个质点的质量,假设此点离某轴线的垂距为k,刚体对该轴线的转动惯量与该等效质点对此同一轴线的转动惯量相等,即I=mk^2,则k称为该刚体对该轴线的回转半径。
回转半径的大小与截面的形心轴有关。
最小回转半径一般指非对称截面中(如不等边角钢),对两个形心轴的回转半径中的较小者。
这在计算构件的长细比时,如构件的平面内和平面外计算长度相等时,它的长细比就要用最小回转半径计算。
长细比是指杆件的计算长度与杆件截面的回转半径之比。
注意,是杆件的计算长度,计算长度与杆件端部的连接方式有关,如固接、铰接、链接、自由,长细比并不是长边与短边之比。
编辑本段运用长柱子钢筋混凝土偏心受压长柱子承载力计算要考虑到外载作用下,因构件弹塑性变性引起的附加偏心的影响,偏心距增大系数与轴心受压构件的稳定系数,都与长细比有关。
短柱子柱子还由于长细比来分为短柱子,长柱子和细长柱子。
根据这我们来判别柱子类型,在实际中就可以尽量避免使用细长柱。
2-5 钢结构计算2-5-1 钢结构计算用表为保证承重结构的承载能力和防止在一定条件下出现脆性破坏,应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑,选用合适的钢材牌号和材性。
承重结构的钢材宜采用Q235钢、Q345钢、Q390钢和Q420钢,其质量应分别符合现行国家标准《碳素结构钢》GB/T 700和《低合金高强度结构钢》GB/T 1591的规定。
当采用其他牌号的钢材时,尚应符合相应有关标准的规定和要求。
对Q235钢宜选用镇静钢或半镇静钢。
承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证,对焊接结构尚应具有碳含量的合格保证。
焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯试验的合格保证。
对于需要验算疲劳的焊接结构的钢材,应具有常温冲击韧性的合格保证。
当结构工作温度等于或低于0℃但高于-20℃时,Q235钢和Q345钢应具有0℃C冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有-20℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-40℃冲击韧性的合格保证。
对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证,当结构工作温度等于或低于-20℃时,对Q235钢和Q345钢应具有0℃冲击韧性的合格保证;对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。
当焊接承重结构为防止钢材的层状撕裂而采用Z向钢时,其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。
钢材的强度设计值(材料强度的标准值除以抗力分项系数),应根据钢材厚度或直径按表2-77采用。
钢铸件的强度设计值应按表2-78采用。
连接的强度设计值应按表2-79至表2-81采用。
钢材的强度设计值(N/mm2)表2-77注:表中厚度系指计算点的钢材厚度,对轴心受力构件系指截面中较厚板件的厚度。
箱形截面回转半径公式
截面回转半径计算公式:设长为h,宽为b,√(i/A) 其中i=bh³/12。
回转半径又称惯性半径,回转半径是指物体微分质量假设的集中点到转动轴间的距离,它的大小等于转动惯量除总质量后再开平方。
物理上认为,刚体按一定规律分布的质量,在转动中等效于集中在某一点上的一个质点的质量,此点离某轴线的垂距为k,因此,刚体对某一轴线的转动惯量与该等效质点对此同一轴线的转动惯量相等,即I=mk2。
则k称为对该轴线的回转半径。
回转半径的大小与截面的形心轴有关。
最小回转半径一般指非对称截面中(如不等边角钢),对两个形心轴的回转半径中的较小者。
这在计算构件的长细比时,如构件的平面内和平面外计算长度相等时,它的长细比就要用最小回转半径计算。
截面回转半径公式推导在工程和物理学的世界里,有个概念叫做“截面回转半径”,听起来是不是有点高大上?别担心,让我来给你揭开这层神秘的面纱。
想象一下,我们在生活中常常需要转弯,比如开车、骑自行车,这个时候,车轮的转动就离不开一个很重要的参数,那就是回转半径。
简单来说,回转半径就像是你在转动某个物体时,它的“核心”位置,帮助我们理解这个物体转动时的动力学特性。
哎,回转半径跟我们平常的生活有什么关系呢?这可不是天书。
就拿骑自行车来说吧,你骑得越快,转弯的时候你就得提前准备,得心里有个数,不能随便乱拐。
如果没控制好,可能就会像甩葱一般飞出去。
这就是回转半径的魔力。
它让我们在设计和分析结构时能更好地掌握“转”的那一瞬间。
想象一下,建筑师在设计摩天大楼,脑海中就得有个清晰的回转半径,才能保证结构的稳固与安全。
怎么来计算这个回转半径呢?别着急,公式虽然看起来复杂,但咱们可以轻松理解。
一般来说,回转半径和物体的质量分布、几何形状密切相关。
简单地说,越重的东西,它的回转半径就越大,这就像我们平常说的“物以类聚,人以群分”。
如果我们拿一个圆形的物体,比如一个圆盘,计算它的回转半径,实际上就可以用截面惯性矩来进行简单的推导。
乍一看,可能觉得这些专业词汇离我们很远,但放松点,我们一起把它拆开来。
想象一下,截面惯性矩就像是一个“力的收藏夹”,把所有力量的作用点都记录下来。
通过对这个惯性矩的计算,我们就能得出物体在旋转时的稳定性。
这样,你就能明白,回转半径并不是凭空而来的,而是经过一番认真推导的结果。
说白了,回转半径就像是为我们提供了一个“转的好地方”,让物体在旋转时保持平衡。
再想象一下,骑车的时候,如果能预见转弯后的反应,那骑行肯定会轻松不少。
这里还得提到个小细节,回转半径不仅适用于圆形物体,其他形状的物体同样适用。
只要我们有了合适的公式,就能轻松应对各种形状的物体,真是让人拍手叫好。
无论是矩形、三角形,还是那些复杂的异形物体,只要带上心,运用得当,回转半径的计算就不再是难题。