数学分析第十三章二重积分的计算练习题解答

2009大专A 班数学分析第13章二重积分的计算练习题解答一、求下列二重积分： 1.22()d d Rx y x y +⎰⎰, 其中R ：11x -≤≤，11y -≤≤. 解：13111222221111()d d d ()d d 3Ry x y x y x x y y x y x ----⎡⎤+=+=+⎢⎥⎣⎦⎰⎰⎰⎰⎰ 13121028(2)d 4()3333x x x x -=+=+=⎰.2.(32)d d Rx y x y +⎰⎰，其中R 是由坐标轴与2x y +=所围成的闭区域.解: 如图，积分区域可以表示为x 型区域: 02y x ≤≤-,02x ≤≤.于是有(32)d d Rx y x y +⎰⎰22222000d (32)d 3d xxx x y y xy y x --⎡⎤=+=+⎣⎦⎰⎰⎰ 220(422)d x x x =+-⎰2320220(4)33x x x =+-=. 3.cos()d d Rx x y x y +⎰⎰,其中R 是以(0,0)(π,0)(π,π)为顶点的三角形区域.解: 如图，积分区域可以表示为x 型区域: 0y x ≤≤,0x π≤≤.于是有cos()d d Rx x y x y +⎰⎰[]00d cos()d sin()d x xx x x y y x x y x ππ=+=+⎰⎰⎰001(sin 2sin )d d(cos cos 2)2x x x x x x x ππ=-=-⎰⎰ 001113(cos cos 2)(cos cos 2)d (102222x x x x x x ππππ⎡⎤=---=---=-⎢⎥⎣⎦⎰.4.d Rx y ⎰⎰，其中R 是由2y x =与y =所围成的闭区域. 解: 如图.积分区域可以表示为x型区域: 2x y ≤≤,01x ≤≤.于是有d Rx y⎰⎰311202d [3x x x y x y x ==⎰⎰714402()d 3x x x =-⎰111542416()311555x x =-=. xyπxy225.(+)d d Rx y x y ⎰⎰, 其中R ：1x y +≤.解：如图，积分区域为两个x 型区域1R 与2R 之并，其中1R ：11x y x --≤≤+, 10x -≤≤， 1R 2R2R ：11x y x -≤≤-, 01x ≤≤．于是有12(+)d d (+)d d (+)d d RR R x y x y x y x y x y x y =-+⎰⎰⎰⎰⎰⎰01111101d ()d d ()d xxxx x y x y x x y y +-----=-++⎰⎰⎰⎰011122111011()d ()d 22x xx x y x x y x x +----+-=-++⎰⎰ 012210112[1(21)]d [1(21)]d 223x x x x -=-++--=⎰⎰． 6.22()d d Rxy x x y +-⎰⎰，其中R 是由直线2y =,y x =及2y x =所围成的闭区域.解: 如图，积分区域可以表示为y 型区域:2yx y ≤≤,02y ≤≤. 于是有22()d d Rx y x x y +-⎰⎰ 322222222d ()d d 32yy y y x x y x y x x y x y ⎡⎤=+-=+-⎢⎥⎣⎦⎰⎰⎰232019313()d 2486y y y =-=⎰． 7.d d 1Rxx y y +⎰⎰，其中R 是由21y x =+,2y x =及0x =所围成的闭区域. 解：如图，积分区域可以表示为x 型区域: 221x y x ≤≤+,01x ≤≤.于是有d d 1Rxx y y +⎰⎰22111120201d d [ln(1)]d 1x x x xx x y x y x y ++==++⎰⎰⎰ 1120ln(2)d ln(21)d x x x x x x =+-+⎰⎰91ln 3ln 282=--．xy1y 18.sin d d Rx x y x ⎰⎰，其中R 是由直线y x =,2xy =及2x =所围成的闭区域. 解：将二重积分化为先y 后x 的累次积分．积分区域可表示为x 型区域: 2xy x ≤≤,02x ≤≤（如图）．故sin d d Rxx y x ⎰⎰22002sin 11d d sin d (1cos 2)22x x x x y x x x ===-⎰⎰⎰． 9.2sin d d Ry x y ⎰⎰，其中R 是由直线y x =,1y =及0x =所围成的闭区域.解：将二重积分化为先x 后y 的累次积分．积分区域可表示为y 型区域: 0x y ≤≤,01y ≤≤（如图）．故2sin d d Ry x y ⎰⎰11220001sin d d sin d (1cos1)2y y y x y y y ===-⎰⎰⎰． 10.2d d yRe x y -⎰⎰，其中R 是由直线1y x =-,2y =及1x =所围成的闭区域. 解：将二重积分化为先x 后y 的累次积分．积分区域可表示为y 型区域: 11x y ≤≤+,02y ≤≤（如图）．故2d d y Rex y -⎰⎰222124011d d d (1)2yy y ey x yey e +---===-⎰⎰⎰．二、将二重积分(,)d d Rf x y x y ⎰⎰化为不同次序的累次积分，其中区域R 分别是：1.由直线y x =及抛物线24y x =所围成. 解：积分区域如图．(1) 将二重积分化为先x 后y 的累次积分积分区域为y 型区域: 24y x y ≤≤,04y ≤≤,于是有(,)d d Rf x y x y ⎰⎰2404d (,)d yy y f x y x =⎰⎰．(2) 将二重积分化为先y 后x 的累次积分积分区域为x型区域: x y ≤≤,04x ≤≤,于是有(,)d d Rf x y x y⎰⎰4d (,)d xx f x y y =⎰⎰．y22xy11yy2312.由x 轴及半圆周222x y r +=(0)y ≥所围成. 解：积分区域如图，有(,)d d Rf x y x y⎰⎰0d (,)d rrx f x y y -=⎰d (,)d ry f x y x =⎰．3.环形闭区域:2214x y ≤+≤.解：积分区域如图．可分成4个小的x 型区域(或y 型区域),于是有(,)d d Rf x y x y⎰⎰1111d (,)d d (,)d x f x y y x f x y y --=+⎰⎰⎰1221d (,)d d (,)d x f x y y x f x y y --++⎰⎰.或(,)d d Rf x y x y⎰⎰1111d (,)d d (,)d y f x y x y f x y x --=+⎰⎰⎰1221d (,)d d (,)d y f x y x y f x y x --++⎰⎰．4.由双曲线2xy =,抛物线21y x =+及直线2x =所围成. 解：积分区域如图．表示为x 型区域:221y x x≤≤+,12x ≤≤, 有(,)d d Rf x y x y ⎰⎰22121d (,)d x xx f x y y +=⎰⎰．表示为两个y 型区域: 1R ：22x y≤≤,12y ≤≤； 2R2x ≤≤,25y ≤≤,有(,)d d Rf x y x y⎰⎰2252212d (,)d d (,)d yy f x y x y f x y x =+⎰⎰⎰．5.由圆222x y x +=,224x y x +=及直线y x =,0y =所围成. 解：积分区域如图．可以表示为两个x 型区域: 1Ry x ≤≤,12x ≤≤；2R：0y ≤≤24x ≤≤,xyxy15221x有(,)d d Rf x y x y⎰⎰2412d (,)d d (,)d x x f x y y x f x y y =+⎰⎰．可以表示为两个y 型区域:1R：12x +≤≤,01y ≤≤； 2R：2y x ≤≤, 12y ≤≤,有(,)d d R f x y x y ⎰⎰1222011d (,)d d (,)d yy f x y x y f x y x =+⎰⎰⎰⎰．三、改变下列累次积分的积分次序： 1.1d (,)d yy f x y x ⎰⎰.解: 所给累次积分为先x 后y 的积分,积分区域为:0x y ≤≤,01y ≤≤,(如图).改变积分次序,积分区域可以表示为: 1x y ≤≤,01x ≤≤,于是有10d (,)d yy f x y x ⎰⎰(,)d d Df x y x y =⎰⎰11d (,)d xx f x y y =⎰⎰.2.2220d (,)d yyy f x y x ⎰⎰.解: 所给累次积分为先x 后y 的积分,积分区域为:22y x y ≤≤,02y ≤≤,(如图).改变积分次序,积分区域可以表示为:2xy ≤≤,04x ≤≤,于是有 2220d (,)d y yy f x y x ⎰⎰402d (,)d x x f x y y =⎰⎰.3.ln 1d (,)d exx f x y y ⎰⎰.解: 所给累次积分为先y 后x 的积分,积分区域为:0ln y x ≤≤,1x e ≤≤,(如图).x改变积分次序,积分区域可以表示为:ye x e ≤≤,01y ≤≤,于是有ln 1d (,)de xx f x y y ⎰⎰10d (,)d y eey f x y x =⎰⎰.4.πsin 0sin2d (,)d xx x f x y y -⎰⎰.解: 所给累次积分为先y 后x 的积分,积分区域为:sinsin 2xy x -≤≤,0x π≤≤,(如图). 改变积分次序, 积分区域为两个y 型区域1D 与2D 之并，其中1D ：arcsin arcsin y x y π≤≤-, 01y ≤≤，2D ：2arcsin y x π-≤≤, 10y -≤≤，于是有 πsin 0sin2d (,)d xx x f x y y -⎰⎰1arcsin 00arcsin 12arcsin d (,)d d (,)d yyyy f x y x y f x y x ππ---=+⎰⎰⎰⎰.5.12201d (,)d d (,)d xxx f x y y x f x y y -+⎰⎰⎰⎰.解: 所给累次积分为两个先y 后x 的积分之和,故积分区域为两个x 型区域1D 与2D 之并，其中1D ：0y x ≤≤, 01x ≤≤；2D ：02y x ≤≤-, 12x ≤≤．改变积分次序,积分区域可以表示为:2y x y ≤≤-,01y ≤≤,于是有12201d (,)d d (,)d xxx f x y y x f x y y -+⎰⎰⎰⎰120d (,)d y yy f x y x -=⎰⎰.6.11d (,)d x f x y y ⎰.解: 积分区域如图,有原式2121d (,)d d (,)d y y f x y x y f x y x =+⎰⎰⎰.7.12330010d(,)d d(,)dy yy f x y x y f x y x-+⎰⎰⎰⎰.解: 积分区域如图.原式232d(,)dxxx f x y y-=⎰⎰.8.14(4)d(,)dyy f x y x-⎰⎰.解: 积分区域如图.原式204224d(,)dxxx f x y y--+=⎰⎰．9.02222022d(,)d d(,)dx xx f x y y x f x y y +--+⎰⎰⎰⎰.解: 积分区域如图.原式1221200221d(,)d d(,)d d(,)dyyy f x y x y f x y x y f x y x--=++⎰⎰⎰⎰．10.21101d(,)dyyy f x y x+-⎰⎰.解: 积分区域如图.化为先y后x的累次积分,积分区域为两个x型区域1D与2D之并，其中1D：11x y-≤≤, 01x≤≤；2D1y≤≤, 12x≤≤．故原式1121011d(,)d d(,)dxx f x y y x f x y y-=+⎰⎰⎰．xy32y1xyyy=1y x=-。

二重积分习题解答(一) 选择题（在每小题给出的四个选项中，只有一项符合题目要求，选出正确的选项） 1．12200I dy x y dx =⎰，则交换积分次序后得 C 。

（A）1220I dy x y dy =⎰； （B）12203I x y dy =⎰；（C ）2112203x I dx x y dx -=⎰⎰； （D ）2112203x I dx x y dy +=⎰⎰。

2．设积分域为{(,)|11,11}D x y x y =-≤≤-≤≤，则x yDedxdy +=⎰⎰ D. .(A)2)1(-e , (B)21)(2--e e , (C) 42)1(-e , (D) 21)(--e e ;3. 设积分域D 由直线,2,2y x x y x =+==围成，则(,)D f x y dxdy =⎰⎰ C(A)120(,)xx dx f x y dy -⎰⎰, (B) 21(,)yydyf x y dx -⎰⎰, (C) 212(,)xxdx f x y dy -⎰⎰, (D) 1(,)xdx f x y dy ⎰⎰.;4．22x y DI e dxdy --=⎰⎰，D :221x y +≤,化为极坐标形式是 D 。

（A ）221[]r I e dr d πθ-=⎰⎰；（B ）2124[]r I e dr d πθ-=⎰⎰；（C ）21202[]r I e rdr d πθ-=⎰⎰；（D ）221[]r I e rdr d πθ-=⎰⎰。

5. 2DI xy d σ=⎰⎰, 其中22:1D x y +≤的第一象限部分,则 C 。

（A）120I dy dy =⎰； （B ）1120I dx xy dy =⎰⎰；（C）12I dx dy =⎰；（D ）1232cos sin I d r dr πθθθ=⎰⎰。

填空题1.交换二次积分次序，1(,)xI f x y dy =⎰＝ 。

故211(,)(,)yxy I dx f x y dy dy f x y dx ==⎰⎰⎰2．设积分域D 由11,22,x y -≤≤-≤≤围成，则3(2)Dx y dxdy +=⎰⎰ 0 3．设积分域为22{(,)|14,}D x y x y y x =≤+≤≥，则积分22()Df xy dxdy +=⎰⎰在极坐标下的二次积分为 。

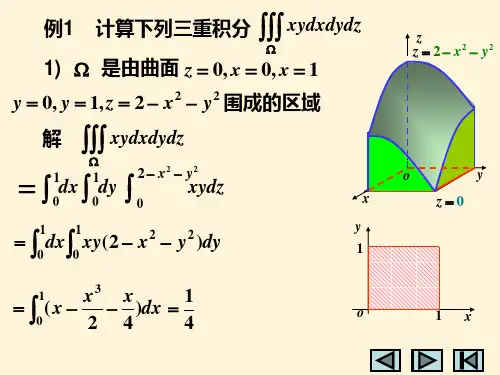
二重积分的计算方法例题及解析一、利用直角坐标计算二重积分1. 例题- 计算∬_D(x + y)dσ，其中D是由直线y = x，y = x^2所围成的闭区域。

2. 解析- （1）首先确定积分区域D的范围：- 联立方程<=ft{begin{array}{l}y = x y = x^2end{array}right.，- 解得<=ft{begin{array}{l}x = 0 y = 0end{array}right.和<=ft{begin{array}{l}x = 1 y = 1end{array}right.。

- 所以在x的范围是0≤slant x≤slant1，对于每一个x，y的范围是x^2≤slant y≤slant x。

- （2）然后将二重积分化为累次积分：- ∬_D(x + y)dσ=∫_0^1dx∫_x^2^x(x + y)dy。

- （3）先计算内层积分：- ∫_x^2^x(x + y)dy=∫_x^2^xxdy+∫_x^2^xydy。

- ∫_x^2^xxdy=x<=ft(y)<=ft.rve rt_x^2^x=x(x - x^2)=x^2-x^3。

- ∫_x^2^xydy=(1)/(2)y^2<=ft.rvert_x^2^x=(1)/(2)(x^2-x^4)。

- 所以∫_x^2^x(x + y)dy=x^2-x^3+(1)/(2)(x^2-x^4)=(3)/(2)x^2-x^3-(1)/(2)x^4。

- （4）再计算外层积分：- ∫_0^1((3)/(2)x^2-x^3-(1)/(2)x^4)dx=(3)/(2)×(1)/(3)x^3-(1)/(4)x^4-(1)/(2)×(1)/(5)x^5<=ft.rvert_0^1。

- =(1)/(2)-(1)/(4)-(1)/(10)=(10 - 5 - 2)/(20)=(3)/(20)。

二重积分的例题及解析二重积分是微积分中的重要概念，用来计算平面区域上的某些特性，比如面积、质量、质心等。

在本文中，我们将介绍一些二重积分的例题，并给出相应的解析。

例题一：计算二重积分 D (x^2 + y^2) dA，其中 D 是由曲线 y = x^2 和 y = 2x - 1 所围成的区域。

解析：首先我们需要确定积分的变量范围。

根据题目的条件，我们可以得到 x 的取值范围为 0 ≤ x ≤ 1，y 的取值范围为 x^2 ≤ y ≤ 2x - 1。

接下来，我们将二重积分转化为两个单重积分。

先对 y 进行积分，再对 x 进行积分。

对 y 进行积分时，积分的上下限根据 y 的取值范围确定，即从 x^2 到 2x - 1。

所以我们得到∫(x^2,2x-1) (x^2 + y^2) dy = [x^2y + (1/3)y^3] |_(x^2,2x-1) = x^2(2x-1) + (1/3)(2x-1)^3 - x^2(x^2) - (1/3)(x^2)^3对 x 进行积分时，积分的上下限根据 x 的取值范围确定，即从 0 到1。

所以我们得到∫(0,1) [x^2(2x-1) + (1/3)(2x-1)^3 - x^2(x^2) - (1/3)(x^2)^3] dx= ∫(0,1) (2x^3 - x^2 + 2x - 1/3) dx= [1/2x^4 - 1/3x^3 + x^2 - 1/3x] |_(0,1)= 1/2 - 1/3 + 1 - 1/3 = 1/6所以二重积分的结果为 1/6。

例题二：计算二重积分 D e^(x+y) dA，其中 D 是由直线 x = 0、y = 0 和 x + y = 1 所围成的区域。

解析：同样，我们首先需要确定积分的变量范围。

根据题目的条件，我们可以得到 x 的取值范围为 0 ≤ x ≤ 1，y 的取值范围为 0 ≤y ≤ 1 - x。

接下来，我们将二重积分转化为两个单重积分。

二重积分练习题一、定义和性质在微积分中，二重积分是对二元函数在给定区域上的积分运算。

它可以看作是对一个平面区域上的函数进行求和。

1. 定义设函数 f(x,y) 在闭区域 D 上有界，将 D 分成若干个小区域ΔDi(i=1,2,...,n)，其中ΔDi 的面积为ΔSi，选定任意一点(xi*, yi*) 属于ΔDi，作数值ΔZi= f(xi*, yi*)ΔSi，当ΔSi 的最大值趋于 0 时，如果和 I 的极限存在，则称 I 为 f(x,y) 在区域 D 上的二重积分，记作：∬ D f(x,y)dS = limΣΔZi2. 性质二重积分具有以下性质：（1）线性性质：对于常数 a 和 b，有∬ D (af(x,y) + bf(x,y))dS = a∬D f(x,y)dS + b∬ D f(x,y)dS（2）可加性：若 D = D1 ∪ D2，则有∬ D f(x,y)dS = ∬ D1 f(x,y)dS + ∬ D2 f(x,y)dS（3）保号性：若f(x,y)≥0，那么∬ D f(x,y)dS ≥ 0二、计算方法1. 求解一般二重积分对于一般的二重积分∬D f(x,y)dS，可以根据具体情况使用极坐标、直角坐标或变量代换等方法进行计算。

下面以几个实例为例进行说明。

例1：计算二重积分∬ D (x^2 + y)dS，其中 D 的边界由直线 y = x和 y = 2 - x 所确定。

解：根据题意，D 的边界可以表示为D = {(x,y) | 0 ≤ x ≤ 1, x ≤ y ≤ 2- x}。

使用直角坐标系计算时，可以将 f(x,y) 中的 x 和 y 分别看作是自变量，然后将 D 投影到 xy 平面得到关于 x 和 y 的积分限。

在本例中，可以先固定 y，让 x 遍历从 0 到 1 的范围，再让 y 遍历从 x 到 2 - x 的范围。

因此，二重积分可以表示为：∫(0,1)∫(x,2-x)(x^2 + y)dydx接下来按照一定的顺序进行积分运算，最终得到结果。

二重积分的基本例题教学内容：利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通过两个定积分的计算(即二次积分)来实现的.一、利用直角坐标计算二重积分我们用几何观点来讨论二重积分的计算问题.讨论中,我们假定；假定积分区域可用不等式表示,其中, 在上连续.据二重积分的几何意义可知,的值等于以为底,以曲面为顶的曲顶柱体的体积.在区间上任意取定一个点,作平行于面的平面,这平面截曲顶柱体所得截面是一个以区间为底,曲线为曲边的曲边梯形,其面积为一般地,过区间上任一点且平行于面的平面截曲顶柱体所得截面的面积为利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为从而有(1)上述积分叫做先对Y,后对X的二次积分,即先把看作常数,只看作的函数,对计算从到的定积分,然后把所得的结果( 它是的函数)再对从到计算定积分.这个先对, 后对的二次积分也常记作在上述讨论中,假定了，利用二重积分的几何意义,导出了二重积分的计算公式(1).但实际上,公式(1)并不受此条件限制,对一般的(在上连续),公式(1)总是成立的.例如:计算解:类似地,如果积分区域可以用下述不等式表示,且函数,在上连续,在上连续,则(2)显然,(2)式是先对,后对的二次积分.二重积分化二次积分时应注意的问题1、积分区域的形状前面所画的两类积分区域的形状具有一个共同点:对于I型(或II型)区域, 用平行于轴(轴)的直线穿过区域内部,直线与区域的边界相交不多于两点.如果积分区域不满足这一条件时,可对区域进行剖分,化归为I型(或II型)区域的并集.2、积分限的确定二重积分化二次积分, 确定两个定积分的限是关键.这里,我们介绍配置二次积分限的方法-- 几何法.画出积分区域的图形(假设的图形如下)在上任取一点,过作平行于轴的直线,该直线穿过区域,与区域的边界有两个交点与,这里的、就是将,看作常数而对积分时的下限和上限；又因是在区间上任意取的,所以再将看作变量而对积分时,积分的下限为、上限为.例1计算,其中是由轴,轴和抛物线在第一象限内所围成的区域.类似地,例2计算, 其中是由抛物线及直线所围成的区域.例3求由曲面及所围成的立体的体积.解: 1、作出该立体的简图, 并确定它在面上的投影区域消去变量得一垂直于面的柱面,立体镶嵌在其中,立体在面的投影区域就是该柱面在面上所围成的区域2、列出体积计算的表达式3、配置积分限, 化二重积分为二次积分并作定积分计算而由,的对称性有所求立体的体积为二、利用极坐标计算二重积分1、变换公式按照二重积分的定义有现研究这一和式极限在极坐标中的形式.用以极点为中心的一族同心圆以及从极点出发的一族射线,将剖分成个小闭区域.除了包含边界点的一些小闭区域外,小闭区域的面积可如下计算其中,表示相邻两圆弧半径的平均值.(数学上可以证明: 包含边界点的那些小闭区域所对应项之和的极限为零, 因此, 这样的一些小区域可以略去不计)在小区域上取点,设该点直角坐标为,据直角坐标与极坐标的关系有于是即由于也常记作, 因此,上述变换公式也可以写成更富有启发性的形式(1)(1)式称之为二重积分由直角坐标变量变换成极坐标变量的变换公式,其中,就是极坐标中的面积元素.(1)式的记忆方法:2、极坐标下的二重积分计算法极坐标系中的二重积分, 同样可以化归为二次积分来计算.【情形一】积分区域可表示成下述形式其中函数, 在上连续.则【情形二】积分区域为下述形式显然,这只是情形一的特殊形式( 即极点在积分区域的边界上).故【情形三】积分区域为下述形式显然,这类区域又是情形二的一种变形( 极点包围在积分区域的内部),可剖分成与,而故则由上面的讨论不难发现, 将二重积分化为极坐标形式进行计算, 其关键之处在于: 将积分区域用极坐标变量表示成如下形式下面通过例子来介绍如何将区域用极坐标变量来表示.例4将下列区域用极坐标变量表示1、2、先画出区域的简图, 据图确定极角的最大变化范围；再过内任一点作射线穿过区域,与区域的边界有两交点,将它们用极坐标表示,这样就得到了极径的变化范围.注: 本题不能利用直角坐标下二重积分计算法来求其精确值.利用此题结果可求出著名概率积分.而被积函数满足,从而以下不等式成立，再利用例二的结果有,,于是不等式可改写成下述形式故当时有,即.3、使用极坐标变换计算二重积分的原则(1)、积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段)；(2)、被积函数表示式用极坐标变量表示较简单( 含, 为实数).例6计算解此积分区域为区域的简图为该区域在极坐标下的表示形式为小结二重积分计算公式直角坐标系下X—型Y—型极坐标系下作业教材161 习题2（I）（2）（3）3（1）（3）4（2）（4）。

第13章重积分§1 有界区域上的重积分1．设一平面薄板（不计其厚度），它在xy平面上的表示是由光滑的简单闭曲线围成的闭区域D．如果该薄板分布有面密度为的电荷，且在D上连续，试用二重积分表示该薄板上的全部电荷．解：设电荷总量为Q，则2．设函数在矩形上有界，而且除了曲线段外，在D上其他点连续．证明f在D上可积．证明：设，将D用平行于两坐标轴的直线分成n个小区域，记，不妨设，将曲线段包含在内，于是在有界闭区域上连续，因此在上可积，即，当时，而当时，取，当时，就有所以f在D上可积．3．按定义计算二重积分，其中解：将D分成n2个小正方形取，则4．设一元函数f（x）在[a,b]上可积，．定义二元函数，证明F（x,y）在D上可积．证明：将[a，b]、[c，d]分别作划分：和则D分成了nm个小矩形记是f（x）在小区间上的振幅，是F在上的振幅，则于是由f（x）在[a，b]上可积，可知，所以即F（x,y）在D上可积．5．设D是R2上的零边界闭区域，二元函数在D上可积．证明和也在D上可积．证明：首先有设，将D划分成n个小区域，利用不等式，可得于是所以由f，g在D上可积，可知即在D上可积．类似地可得从而在D上也可积．§2 重积分的性质与计算1．证明重积分的性质8．证明：不妨设，M、m分别是f（x）在区域Ω上的上确界、下确界，由、性质1和性质3，可得当，积分中值定理显然成立．当，有所以存在，使得即如果f在有界闭区域Ω上连续，由介值定理，存在，使得所以2．根据二重积分的性质，比较下列积分的大小：（1），其中D为x轴、y轴与直线x＋y＝1所围的区域；（2），其中D为闭矩形[3，5]×[0，1]．解：（1）因为在D上成立0＜x＋y＜1，所以，于是（2）因为在D上成立x＋y≥3，所以，于是3．用重积分的性质估计下列重积分的值：（1），其中D为闭矩形[0，1]×[0，1]；（2），其中D为区域（3），其中Ω为单位球解：（1）因为在D上成立，所以（2）因为在D上成立，所以（3）因为在Ω上成立，所以4．计算下列重积分：（1），其中D为闭矩形[0，1]×[0，1]；（2），其中D为闭矩形[a，b]×[c，d]；（3），其中Ω为长方体[1，2]×[1，2]×[1，2]．解：5．在下列积分中改变累次积分的次序：（改成先y方向，再x方向和z方向的次序积分）；（改成先x方向，再y方向和z方向的次序积分）．解：6．计算下列重积分：（1），其中D为抛物线和直线所围的区域；（2），其中D为圆心在（a，a），半径为a并且与坐标轴相切的圆周上较短的一段弧和坐标轴所围的区域；（3），其中D为区域（4），其中D为直线和0）所围的区域；（5），其中D为摆线的一拱与x轴所围的区域；（6），其中D为直线和x＝1所围的区域；。