第三章集中趋势的度量

第三章数据的集中趋势和离散程度教案教案：第三章数据的集中趋势和离散程度一、教学目标：1.理解数据的集中趋势和离散程度的基本概念和含义；2.掌握计算和应用数据的集中趋势和离散程度的方法；3.能够利用数据的集中趋势和离散程度进行数据分析和决策。

二、教学内容：1.集中趋势的度量：众数、中位数、均值；2.离散程度的度量：极差、方差、标准差。

三、教学过程：1.导入（5分钟）教师简要介绍数据的集中趋势和离散程度的概念和定义，激发学生的学习兴趣。

2.集中趋势的度量（20分钟）（1）众数：a.理解众数的概念：数据中出现次数最多的值；b.计算众数的方法：统计数据各项的频数，找出频数最大的数据项。

（2）中位数：a.理解中位数的概念：将数据从小到大排序，中间的数；b.计算中位数的方法：①如果数据个数为奇数，中位数可直接取排序后的中间值；②如果数据个数为偶数，中位数可取排序后的中间两个数的平均值。

（3）均值：a.理解均值的概念：数据的算术平均值；b.计算均值的方法：将数据项相加，再除以数据的个数。

3.离散程度的度量（30分钟）（1）极差：a.理解极差的概念：数据的最大值与最小值之差；b.计算极差的方法：将数据按升序排列，最大值减去最小值。

（2）方差：a.理解方差的概念：数据偏离均值的平均平方差；b.计算方差的方法：将每个数据与均值之差的平方相加，再除以数据个数。

（3）标准差：a.理解标准差的概念：方差的正平方根；b.计算标准差的方法：取方差的正平方根。

4.应用案例分析（25分钟）教师提供实际数据，并引导学生运用所学知识计算数据的集中趋势和离散程度，分析数据的特点和规律。

例如，一个班级的学生成绩：70、75、80、85、90，学生的身高：160cm、165cm、170cm、175cm、180cm。

5.总结（5分钟）教师对本节课所学内容进行总结，并强调数据的集中趋势和离散程度对数据分析和决策的重要性。

同时，鼓励学生在实践中灵活应用所学知识。

【课程讲义】第三章集中量数【教学目标】明确一批数据的特征包括两个方面的内容：集中趋势、离散性；明确集中量数是描述数据集中趋势的量数，可以作为一批数据的代表值；明确算术平均数是所有集中量数中运用最广泛、最优的量数；明确各种集中量数的含义、计算方法、使用条件、性质及优缺点。

【学习方法】了解、理解、计算与应用。

【重点难点】算术平均数的概念及适用条件；算术平均数的计算方法；中位数的概念及适用条件；中位数的计算方法。

【讲义内容】前一章所讲的统计分组、统计表、统计图等，只是对研究工作中所获得的数据进行初步整理，其目的是对数据的性质、分布特征、差异情况及数据的一般规律有一直观和形象的认识。

因此说这一步还不是应用统计方法的步骤。

为了进一步发现和表示一组数据的规律性，需要计算出一些能够反映这组数据的统计特征的数字——称为统计量或特征数。

对于一组数据来讲，最常用的统计量有两类。

一类是表现数据集中性质或集中程度的，另一类是表现数据分散性质或分散程度的。

数据的集中情况指一组数据的中心位置。

集中趋势的度量，即确定一组数据的代表值。

描述数据集中情况的统计量有多种，包括算术平均数、中数、几何平均数等。

由于这些统计量的作用在于度量数据的集中趋势，因此它们都称为集中量数。

本章主要介绍几种常用的集中量数。

集中量数只描述数据的集中趋势和典型情况，它还不能说明一组数据的全貌。

数据除典型情况之外，还有变异性的特点。

对于数据变异性即离中趋势进行度量的一组统计量，称作差异量数，这些差异量数有方差、标准差、全距、平均差、四分差及各种百分差等等，下一章中将对常用的差异量数进行介绍。

第一节 算术平均数一、算术平均数的概念和适用条件（一）概念算术平均数一般简称为平均数或均数（Mean ）。

只有在与其他几种集中量数如几何平均数、加权平均数相区别的时候，才把它叫做算术平均数。

如果平均数是由X 变量计算的，就记为X （读作X 杠），若由Y 变量求得，则记为Y 。

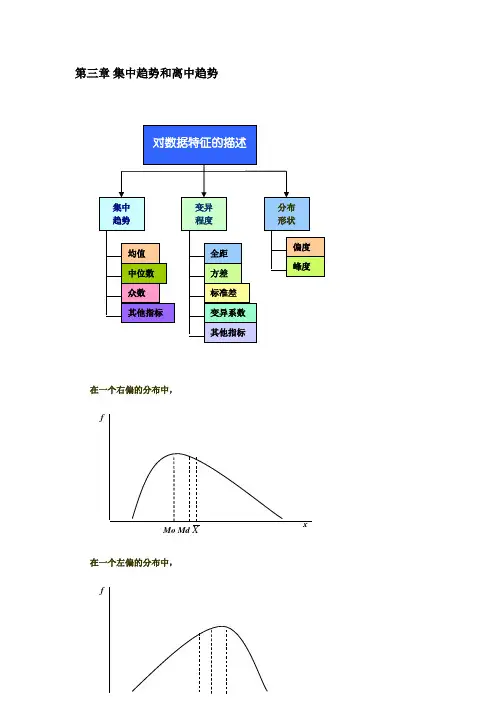
第三章 集中趋势和离中趋势在一个右偏的分布中，在一个左偏的分布中，xX Md Mo§2 离中趋势的计量与集中趋势相反，离中趋势反映的是一组资料中各观测值之间的差异或离散程度。

一、全距（Range ）全距又称极差，指一组资料中最大的数值与最小的数值之差。

Ｒ ＝ 最大值－最小值简单明了，但没有考虑中间值以及数据的分布情况。

二、平均差（Average Deviation ）1、一组数据值与其均值之差的绝对值的平均数称为平均差。

以Ａ.D.表示，其计算公式为：对于未分组资料：nXX D A ni i ∑=-=1..对于分组资料：∑∑=-=iii ii f f XX D A 1..例4.12 某企业100名工人的每周工资资料如下：100名工人每周工资资料 按工资分组 人数 组中值 离差 离差的 绝对值 离差绝对值×次数 100—200 10 150 -170 170 1700 200─300 30 250 -70 70 2100 300─400 40 350 30 30 1200 400─500 20 450 130 130 2600 合计100－——7600则： x =x f fi iii i∑∑=3200100=320（元） A.D. =x x ffi iii i-∑∑=7600100=76（元） 平均差充分考虑了每一个数值离中的情况，完整地反映了全部数值的分散程度，在反映离中趋势方面比较灵敏，计算方法也比较简单。

它的缺陷在于，由于它的敏感性，使得它易受极端值影响，特别是绝对值运算给数学处理带来很多不便。

2、在ECXCEL 中计算平均差 未分组资料：函数A VEDEV分组资料：运用函数：SUMPRODUCT, ABS （求绝对值）三、方差（Variance ）与标准差（Standard Deviation ） 方差与标准差是测度离中趋势的最重要、最常用的量。

1、总体方差是一组资料中各数值与其算术平均数离差平方和的平均数。

第三章 数据分布特征的度量第一节 一.集中趋势 （一）概念：指一组数据向某一中心值靠拢的倾向，测度集中趋势也就是要寻找数据一般水平的代表值或中心值。

（二）特点：1.集中趋势测度值是一个代表性值，表示被研究总体的一般水平（数据的共性）2.平均数把被研究总体的数量标志值在各个单位之间的数量差异抽象化了 （三）作用：1.利用集中趋势测度值对比不同总体的一般水平2.利用集中趋势测度值比较.反映同一单位某一标志不同时期一般水平的发展变化，说明事物的发展过程和变化趋势3.利用集中趋势测度值分析现象之间的相互关系，并推算其它有关的指标。

（四）度量Ⅰ.数值均值（μ） 1.算术均值 （1）特点：①集中趋势的最常用测度值 ②一组数据的均衡点所在 ③体现了数据的必然性特征 ④易受极端值的影响 （2）数学性质：①数值观测值与算术均值的离差之和等于0 ∑=-0)(μx 或 ∑=-0)(f x μ ②数值观测值与算术均值的离差平方和最小∑=-min )(2μx 或∑=-min )(2f x μ③均值易受极端值的影响2.调和均值（H ） （1）特点：①调和均值是各个变量值倒数的算术均值的倒数 ②易受极端值的影响3.几何均值（G）（1）特点：①适用于对比率数据的平均②主要用于计算平均速度Ⅱ.位置均值1.众数（M o）（1）概念：一组数据中出现次数最多的变量值,Mo表示（2）特点①众数的值与相邻两组频数的分布有关②用于数值型分组数据，适合于数据量较多时使用③不受极端值的影响④一组数据可能没有众数或有几个众数（不唯一性）2.中位数（M e）（1）概念：依据数据从小到大排序后，处于中间位置上的变量值，用Me表示（2）特点：①不受极端值影响②数据分布偏斜程度较大时应用绝对值之和为最小（中位数与各数据的距离之和最短）③各变量值与中位数的离差3.分位数（Q）（1）概念：是将全部数据排序后等分为若干个分位点，各分位点上的数值称为分位数（五）算术均值与众数和中位数的关系第二节数据离中程度的度量一.离散程度（一）概念：测量一组数据差异程度，反应频数分布数列中各个数据的变动范围或差异程度。

每天一点统计学——数据集中趋势的量度
在统计学中，把握数据的集中趋势，对于了解事物的本质特征、掌握事物发展变化的规律，具有非常重要的作用。

均值、中位数和众数能很好地量度数据的集中趋势。

均值
均值又叫算数平均数，它分为简单算术平均数、加权算术平均数。

它主要适用于数值型数据（像重量、长度、时间等只能用数字描述的数据），不适用于类别数据（描述事物性质或特征的数据）。

就是将一组数据的和除以数据的个数。

它在统计学中有一个专门的符号：μ（读“谬”）。

简单算数平均数，主要用于未分组的原始数据，计算公式为：
加权算术平均，主要用于处理经分组整理的数据（分组的数据又叫做“频数”），计算公式为：
中位数
把一些数据按照高低排序后找出正中间的一个数值，叫做中位数。

求中位数三步法：
1.按顺序排列数字，从最小值排列到最大值。

2.如果有奇数个数值，则中位数为位于中间的数值。

如有n个数，则中间数的位置为（n+1）/2。

3.如果有偶数个数值，则将两个中间数相加，然后除以2。

中间位置的算法是：（n+1)/2。

兩个中间数分别位于这个中间位置的两侧。

众数
众数是一组数据中出现次数最频繁的数值，代表数据的一般水平。

如果在一组数据中，只有一个变量值出现次数最多，则变量值即为众数;如果有两个(或多个)变量值出现次数相同并最多，那么，两个(或多个)变量值都是众数;如果有两个(或多个)变量值出现次数最多但不相同，则出现次数最多的数值是主要众数，其他为次要众数。

当然数据中变
量值出现的次数都相同，则该数据没有众数。

集中趋势的度量指标
一、集中趋势的度量指标
1、算术平均数（arithmetic mean）
算术平均数是指把一组数据相加，然后除以数据的个数得出的结果。

它反映出一组数据的中心位置，是集中趋势的最常用度量指标。

2、几何平均数（geometric mean）
几何平均数是指在一组数据中，给定一个数组，把这组数据的每个值的指数取出，然后这些指数的乘积除以数据的个数，得出的结果就是这组数据的几何平均数。

3、中位数（median）
中位数是指从小到大排列这组数据，得出排在中间位置的那个数，叫做中位数。

它反映出一组数据的集中程度，也反映出这组数据的分布形态，如果是正态分布则中位数等于算术平均数。

4、众数（mode）
众数是指一组数据中出现次数最多的数字，它反映出这组数据的分布形态，如果是正态分布则众数等于算术平均数。

5、变异系数（coefficient of variation）
变异系数是指样本标准差除以样本均值，反映出数据的离散程度，它具有一定的可比性。

如果变异系数越小，则数据越集中，越接近于正态分布，反之，变异系数越大，数据的集中程度就越低。

- 1 -。