数据的集中趋势与离散程度(非常全面)

数据的集中趋势和离散程度【知识点1】正确理解平均数、众数和中位数的概念一、平均数：平均数是反映一组数据的平均水平的特征数，反映一组数据的集中趋势．平均数的大小与一组数据里的每一个数据都有关系，任何一个数据的变化都会引起平均数的变化．例1：有四个数每次取三个数,算出它们的平均数再加上另一个数,用这种方法计算了四次,分别得到以下四个数:86, 92, 100, 106, 那么原4个数的平均数是________ .例2：有几位同学参加语文考试,赵峰的得分如果再提高13分,他们的平均分就到达90分,如果赵峰的得分降低5分,他们的平均分就只得87分,那么这些同学共有________人.例3：有5个数,其平均数为138,按从小到大排列,从小端开始前3个数的平均数为127,从大端开始顺次取出3个数,其平均数为148,那么第三个数是_______ .例4：某5个数的平均值为60,假设把其中一个数改为80,平均值为70,这个数是________ .例10：某人沿一条长为12千米的路上山，又从原路返回，上山的速度是2千米/小时，下山的速度是6千米/小时。

那么，他在上山和下山的全过程当中的平均速度是多少千米每小时？例11：假设不选择教材中的引入问题，也可以替换成更贴近学生学习生活中的实例，下举一例可供借鉴参考。

求该校初二年级在这次数学考试中的平均成绩？二、众数：在一组数据中出现次数最多的数据叫做这一组数据的众数．一组数据中的众数有时不唯一．众数着眼于对各数出现的次数的考察，这就告诉我们在求一组数据的众数时，既不需要排列，又不需要计算，只要能找出样本中出现次数最多的那一个〔或几个〕数据就可以了．当一组数据中有数据屡次重复出现时，它的众数也就是我们所要关心的一种集中趋势．注：众数是数据中出现次数最多的数据，是一组数据中的原数据，而不是相应的次数．众数有可能不唯一，注意不要遗漏．例12：在一次数学测验中，甲、乙、丙、丁四位同学的分数分别是90、x 、90、70，假设这四个同学得分的众数与平均数恰好相等，那么他们得分的中位数是【 】A 、100 B 、90 C 、80 D 、70 例13：当5个整数从小到大排列，其中位数是4，如果这组数据的唯一众数是6，那么5个整数可能的最大的和是【 】A 、21 B 、22 C 、23 D 、24例14：10名工人，某天生产同一零件，生产到达件数是：15，17，14，10，15，19，17，16，14，12，那么这一组数据的众数是【 】A 、15 B 、17 15 C 、14 D 、17 15 14 例15：〔1〕计算这9双鞋尺码的平均数、中位数和众数.〔2〕哪一个指标是鞋厂最感兴趣的指标？哪一个指标是鞋厂最不感兴趣的？三、中位数：是将一组数据按大小顺序排列后，处在最中间的一个数〔或处在最中间的两个数的平均数〕．一组数据中的中位数是唯一的． 注：求中位数要先把数据按大小顺序排列，可以从小到大，也可以从大到小．如果数据个数n 为奇数时，第21+n 个数据为中位数；如果数据个数n 为偶数时，第2n 、12+n 个数据的平均数为中位数．例16：李大伯承包了一个果园，种植了100棵樱桃树，今年已进入收获期．收获时，从中任选并采摘了10棵树的樱桃，分别称得每据调查，市场上今年樱桃的批发价格为每千克15元．用所学的统计知识估计今年此果园樱桃的总产量与按批发价格销售樱桃所得的总收入分别约为【 】A ．200千克，3000元B ．1900千克，28500元C ． 2000千克，30000元D ．1850千克，27750元〔1〕该班学生每周做家务劳动的平均时间是多少小时？〔2〕这组数据的中位数、众数分别是多少?〔3〕请你根据〔1〕、〔2〕的结果，用一句话谈谈自己的感受．【知识点2】极差、方差和标准差极差、方差和标准差都是用来研究一组数据的离散程度的，反映一组数据的波动范围或波动大小的量.一、极差一组数据中最大值与最小值的差叫做这组数据的极差，即极差=最大值-最小值.极差能够反映数据的变化范围，实际生活中我们经常用到极差.如一支足球队队员中的最大年龄与最小年龄的差，一个公司成员中最高收入与最低收入的差等都是极差的例子.极差是最简单的一种度量数据波动情况的量，它受极端值的影响较大.二、方差方差是反映一组数据的整体波动大小的特征的量.它是指一组数据中各个数据与这组数据的平均数的差的平方的平均数，它反映的是一组数据偏离平均值的情况.方差越大，数据的波动越大方差越小数据的波动越小. 求一组数据的方差可以简记先求平均，再求差，然后平方，最后求平均数.一组数据x 1、x 2、x 3、…、x n 的平均数为x ，那么该组数据方差的计算公式为：])()()[(1222212x x x x x x nS n -++-+-= . 例18：数据0、1、2、3、x 的平均数是2，那么这组数据的极差和标准差分别是【 】A 4，2B 4，2C 2，10D 4，10三、标准差在计算方差的过程中，可以看出方差的数量单位与原数据的单位不一致，在实际的应用时常常将求出的方差再开平方，此时得到量为这组数据的标准差.即标准差=方差. 例19：数据90，91，92，93的标准差是【 】〔A 〕 2 〔B 〕54 〔C 〕54 〔D 〕52✪注意：极差、方差、标准差的关系方差和标准差都是用来描述一组数据波动情况的量，常用来比拟两组数据的波动大小.两组数据中极差大的那一组并不一定方差也大.在实际问题中有时用到标准差，是因为标准差的单位和原数据的单位一致，且能缓解方差过大或过小的现象.例20：从甲、乙两种玉米苗中各抽10株，分别测得它们的株高如下：〔单位：cm 〕甲： 21 42 39 14 19 22 37 41 40 25乙： 27 16 40 41 16 44 40 40 27 44(1)根据以上数据分别求甲、乙两种玉米的极差、方差和标准差.(2)哪种玉米的苗长得高些;(3)哪种玉米的苗长得齐.例21：市体校准备挑选一名跳高运发动参加全市中学生运动会，对跳高运动队的甲、乙两名运发动进行了8次选拔比赛.他们的成绩〔单位：m 〕如下：甲：1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67乙：1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75(1)甲、乙两名运发动的跳高平均成绩分别是多少？(2)哪位运发动的成绩更为稳定？(3)假设预测，跳过1.65m 就很可能获得冠军，该校为了获得冠军，可能选哪位运发动参赛？假设预测跳过1.70m 才能得冠军呢？。

数据的中心趋势和离散程度数据分析是现代社会中不可或缺的一部分，它帮助我们理解和解释各种现象。

在数据分析中，了解数据的中心趋势和离散程度是非常重要的。

本文将介绍数据的中心趋势和离散程度的概念，并提供几种用于测量的方法。

一、中心趋势中心趋势是一组数据集中的一个值，它代表了数据的平均水平或核心位置。

最常用的中心趋势度量是算术平均数或平均值。

平均数被定义为一组数值之和除以该组数值的数量。

例如，给定一组数值：2, 4, 6, 8, 10，它们的平均数为6。

另一个常用的中心趋势度量是中位数。

中位数是将一组数据按照大小顺序排列后，位于中间位置的值。

如果数据集中有偶数个数值，则中位数为中间两个数值的平均值。

例如，给定一组数值：2, 4, 6, 8，它们的中位数为5。

除了平均数和中位数，还有一种用于测量中心趋势的度量是众数。

众数是数据集中出现频率最高的数字。

如果数据集中存在多个众数，则称为多峰分布。

例如，给定一组数值：2, 2, 4, 6, 8，它们的众数为2。

二、离散程度离散程度描述了数据集中数值的分散程度或散布范围。

如果数据集中的数值都非常接近，那么离散程度很小；如果数值相差很大，那么离散程度很大。

最常用的离散程度度量是方差和标准差。

方差是每个数值与平均数之差的平方的平均值。

标准差是方差的平方根。

方差和标准差越大，表示数据集的离散程度越大。

例如，给定一组数值：2, 4, 6, 8, 10，它们的方差为8，标准差为2.83。

这意味着这组数据的离散程度相对较小。

而如果给定一组数值：2, 2, 4, 6, 20，它们的方差为56，标准差为7.48。

这组数据的离散程度较大。

除了方差和标准差，还有其他一些度量离散程度的方法，例如范围和百分位数。

范围是数据集的最大值和最小值之间的差值。

百分位数是将数据集按大小顺序排列后，某个百分比处的数值。

例如，第75百分位数是将数据集分为四个相等的部分后，处于第三个部分的数值。

总结：在数据分析中，了解数据的中心趋势和离散程度是非常重要的。

数据的集中趋势与离散程度统计学中，描述和衡量数据分布特征的两个重要方面是集中趋势和离散程度。

集中趋势指的是数据集中在哪个数值附近，而离散程度描述了数据的分散程度。

在本文中，我将详细介绍集中趋势和离散程度的定义、常用的衡量指标和如何应用。

一、集中趋势集中趋势是指数据集中在哪个数值处的趋势或位置，常用的衡量指标包括均值、中位数和众数。

1. 均值均值是数据集所有观测值的算术平均数。

它是最常用的衡量集中趋势的指标。

计算均值的方法是将所有观测值相加，再除以观测值的个数。

均值受极端值的影响较大。

2. 中位数中位数是将数据集按照大小排序后，位于中间位置的观测值。

如果数据集的个数是奇数，则中位数就是排序后位于中间的观测值；如果数据集的个数是偶数，则中位数是中间两个观测值的平均数。

中位数对极端值不敏感，更能反映数据的典型情况。

3. 众数众数是数据集中出现频率最高的观测值。

一个数据集可能存在一个众数，也可能存在多个众数，或者没有众数。

众数主要用于描述离散型数据。

二、离散程度离散程度是描述数据分散程度的指标，常用的衡量指标包括极差、方差和标准差。

1. 极差极差是数据集中最大观测值和最小观测值之间的差值。

极差越大，表示数据的离散程度越大；极差越小，表示数据的离散程度越小。

极差对极端值非常敏感。

2. 方差方差是数据集观测值与均值之差的平方的平均值。

方差衡量了数据与其均值之间的离散程度，数值越大表示数据的离散程度越大，反之亦然。

方差对极端值非常敏感。

3. 标准差标准差是方差的平方根，用于衡量数据集的离散程度。

标准差具有与原始数据相同的度量单位，比方差更容易解释和理解。

标准差越大，表示数据的离散程度越大，反之亦然。

三、应用集中趋势和离散程度的概念和指标在各个领域具有广泛的应用。

在金融领域，通过分析股票价格的均值和离散程度，可以评估股票的风险和收益。

在市场调研中，通过分析产品价格的中位数和标准差，可以了解市场需求和产品价值的稳定性。

数据的集中趋势与离散程度在我们的日常生活和各种工作领域中，数据无处不在。

无论是研究经济趋势、评估学生的考试成绩，还是分析市场销售数据，了解数据的特征都是至关重要的。

而数据的集中趋势和离散程度就是两个关键的特征，它们能帮助我们更好地理解数据所蕴含的信息。

先来说说数据的集中趋势。

简单来讲，集中趋势就是数据呈现出的一种“聚集”的特点，反映了数据的中心位置或者一般水平。

最常见的用于描述集中趋势的指标有平均数、中位数和众数。

平均数，大家应该都很熟悉。

就是把一组数据的所有数值加起来，然后除以数据的个数。

比如说，一个班级里五位同学的数学考试成绩分别是 80 分、90 分、85 分、75 分和 95 分，那么他们的平均成绩就是（80 ＋ 90 ＋ 85 ＋ 75 ＋ 95）÷ 5 ＝ 85 分。

平均数很容易计算，也能直观地反映出这组数据的大致水平。

中位数呢，是将一组数据按照从小到大或者从大到小的顺序排列，如果数据的个数是奇数，那么处于中间位置的那个数就是中位数；如果数据的个数是偶数，那么中间两个数的平均值就是中位数。

比如，还是上面那五个同学的成绩，从小到大排列为 75 分、80 分、85 分、90 分、95 分，因为数据个数是奇数，所以中位数就是 85 分。

中位数的优点在于，它不受极端值的影响。

比如，如果有一个同学考了20 分，那么这组数据的平均数就会被拉低很多，但中位数却不会受到太大影响。

众数则是一组数据中出现次数最多的那个数值。

比如说，一组数据是 1，2，2，3，3，3，4，4，4，4，那么众数就是 4。

众数可以反映出数据中最常见的情况。

了解了数据的集中趋势，我们再来看数据的离散程度。

离散程度反映的是数据的分散情况，也就是数据相对于中心位置的偏离程度。

常见的描述离散程度的指标有极差、方差和标准差。

极差是一组数据中的最大值减去最小值。

比如，一组数据是 10，20，30，40，50，那么极差就是 50 10 ＝ 40。

理解数据的集中趋势与离散程度数据是我们生活中不可或缺的一部分，无论是在科学研究、商业决策还是个人生活中，我们都需要处理和分析大量的数据。

在数据分析过程中，了解数据的集中趋势和离散程度是非常重要的，它们能够帮助我们更好地理解数据的分布和特征。

一、集中趋势集中趋势是指数据分布中心的位置，常用的集中趋势度量指标有均值、中位数和众数。

均值是一组数据的平均值，通过将所有数据相加再除以数据个数得到。

均值能够反映数据的总体水平，但受到极端值的影响较大。

例如，考虑一个班级的学生成绩，大部分学生的成绩在70-90分之间，但有一个学生得了100分，这个极端值会使得均值偏高。

中位数是将一组数据按照大小顺序排列后，位于中间位置的数值。

中位数不受极端值的影响，更能反映数据的典型值。

在上述例子中，中位数仍然能够准确地反映学生的典型成绩水平。

众数是一组数据中出现次数最多的数值，它代表了数据分布的最高峰。

众数适用于描述离散型数据，如人口统计中的年龄分布。

二、离散程度离散程度是指数据分布的分散程度，常用的离散程度度量指标有范围、方差和标准差。

范围是一组数据的最大值与最小值之间的差距，它能够直观地反映数据的离散程度。

然而，范围只考虑了极端值，没有考虑其他数据的分布情况。

方差是一组数据与其均值之差的平方的平均值，它能够反映数据与均值之间的差异。

方差越大，数据的离散程度越高。

标准差是方差的平方根，它具有与原始数据相同的单位。

标准差能够衡量数据的离散程度，并且与均值具有相同的量纲，因此更容易进行比较和解释。

三、应用举例理解数据的集中趋势和离散程度在各个领域都有广泛的应用。

在金融领域，我们可以通过分析股票的收益率来了解市场的集中趋势和离散程度。

均值和中位数能够帮助我们了解市场的平均收益水平，而标准差则能够反映市场的波动性。

这些指标对于投资者制定投资策略和管理风险非常重要。

在医学研究中，我们可以通过分析患者的生命体征数据来了解疾病的发展趋势和离散程度。

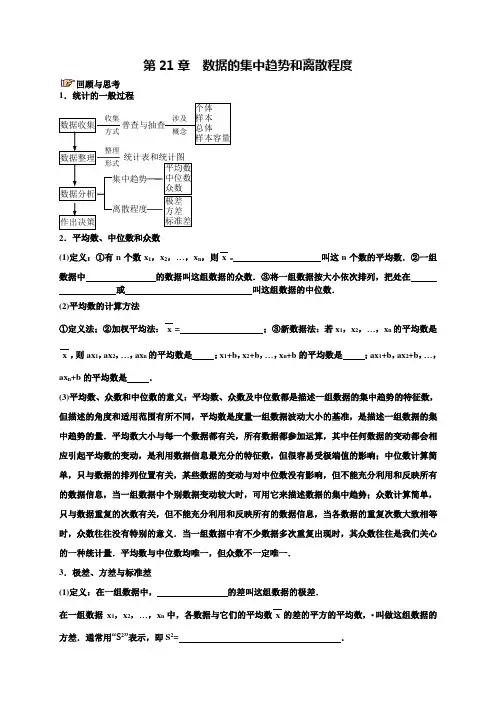
第21章 数据的集中趋势和离散程度回顾与思考 1．统计的一般过程2．平均数、中位数和众数(1)定义：①有n 个数x 1，x 2，…，x n ，则x= 叫这n 个数的平均数．②一组数据中 的数据叫这组数据的众数．③将一组数据按大小依次排列，把处在 或 叫这组数据的中位数． (2)平均数的计算方法①定义法；②加权平均法：x = ；③新数据法：若x 1，x 2，…，x n 的平均数是x ，则ax 1，ax 2，…，ax n 的平均数是 ；x 1+b ，x 2+b ，…，x n +b 的平均数是 ；ax 1+b ，ax 2+b ，…，ax n +b 的平均数是 ．(3)平均数、众数和中位数的意义：平均数、众数及中位数都是描述一组数据的集中趋势的特征数，但描述的角度和适用范围有所不同，平均数是度量一组数据波动大小的基准，是描述一组数据的集中趋势的量．平均数大小与每一个数据都有关，所有数据都参加运算，其中任何数据的变动都会相应引起平均数的变动，是利用数据信息最充分的特征数，但很容易受极端值的影响；中位数计算简单，只与数据的排列位置有关，某些数据的变动与对中位数没有影响，但不能充分利用和反映所有的数据信息，当一组数据中个别数据变动较大时，可用它来描述数据的集中趋势；众数计算简单，只与数据重复的次数有关，但不能充分利用和反映所有的数据信息，当各数据的重复次数大致相等时，众数往往没有特别的意义．当一组数据中有不少数据多次重复出现时，其众数往往是我们关心的一种统计量．平均数与中位数均唯一，但众数不一定唯一． 3．极差、方差与标准差(1)定义：在一组数据中， 的差叫这组数据的极差．在一组数据x 1，x 2，…，x n 中，各数据与它们的平均数x 的差的平方的平均数，•叫做这组数据的方差．通常用“S 2”表示，即S 2= ．数据收集数据整理数据分析 作出决策普查与抽查 个体样本总体样本容量 涉及 概念 收集 方式 整理 统计表和统计图形式集中趋势离散程度 平均数 中位数 众数 极差方差标准差方差的叫做这组数据的标准差，用“S”表示，即S= ．(2)方差的计算①基本公式：S2= ；②简化计算公式：S2 = ，也可写成S2= ，此公式的记忆方法是：方差等于原数据平方的平均数减去平均数的平方．③新数据法：若x1，x2，…，x n的方差是s2，标准差是s，则ax1，ax2，…，ax n的方差是，标准差是；x1+b，x2+b，…，x n+b的方差是，标准差是；ax1+b，ax2+b，…，ax n+b 的方差是，标准差是．(3)方差和标准差的意义：方差和标准差都是用来描述一组数据波动情况的特征数，常用来比较两组数据的波动大小，我们所研究的权是这两组数据的个数相等、平均数相等或比较接近时的情况．方差较大的数据波动较大，方差较小的数据波动较小．4．用样本估计总体方法与技能【例1】小明对这家公司有了一定的了解，他决定留下来工作，公司并对员工的工资进行调整。

数据的集中趋势离散程度数据的集中趋势是指数据分布的中心位置，可以通过测量数据的均值、中位数和众数来描述。

数据的离散程度是指数据集中趋势的分散程度，可以通过测量数据的范围、方差和标准差来描述。

首先，数据的集中趋势可以通过均值来衡量。

均值是将所有数据加总后除以数据的个数得到的平均值。

它将数据集中在一个中心位置，可以反映数据的整体水平。

然而，均值容易受到极值的影响，因此需要结合其他指标综合考虑。

中位数是将数据按照大小排序后位于中间位置的值，可以将数据集合分为两部分。

中位数不受极值的影响，适用于有极值存在的情况。

中位数能反映数据的中间位置，相对稳定。

众数是在数据集中出现频率最高的值。

众数可以反映数据的最常见取值，适用于描述离散数据。

其次，数据的离散程度可以通过范围来衡量。

范围是最大值减去最小值，它反映了数据集的变化幅度。

范围简单直观，但不稳定，容易受到极值的影响。

方差是每个数据与均值差的平方的平均数，可以描述数据集与均值的偏离程度。

方差越大，数据越分散；方差越小，数据越集中。

方差让我们能够了解数据集内部的差异。

标准差是方差的平方根，它与均值具有相同的量纲，能更直观地反映数据的离散程度。

标准差比方差更常用，因为它的单位与原始数据相同，易于理解。

数据的集中趋势和离散程度是相互关联的，它们一起能够提供一个完整的数据描述。

例如，在比较两组数据的差异时，可以通过比较均值和标准差来判断其集中趋势和离散程度。

总体而言，数据的集中趋势和离散程度是统计分析中常用的指标，能够提供重要的数据特征，帮助我们理解数据的分布情况，从而进行决策和预测。

在实际应用中，我们需要根据具体情况选择合适的指标，并结合其他分析方法来综合评价数据的集中趋势和离散程度。

（一）知识要点知识点1：表示数据集中趋势的代表平均数、众数、中位数都是描述一组数据集中趋势的特征数，只是描述的角度不同，其中平均数的应用最为广泛。

知识点2：表示数据离散程度的代表极差的定义：一组数据中最大值与最小值的差，能反映这组数据的变化范围，我们就把这样的差叫做极差。

极差=最大值－最小值，一般来说，极差小，则说明数据的波动幅度小。

知识点3：生活中与极差有关的例子在生活中，我们经常用极差来描述一组数据的离散程度，比如一支篮球队队员中最高身高与最矮身高的差。

一家公司成员中最高收入与最低收入的差。

知识点4：平均差的定义在一组数据x1，x2，…，x n中各数据与它们的平均数的差的绝对值的平均数即T=叫做这组数据的“平均差”。

“平均差”能刻画一组数据的离散程度，“平均差”越大，说明数据的离散程度越大。

知识点5：方差的定义在一组数据x1，x2，…，x n中，各数据与它们的平均数差的平方，它们的平均数，即S2=来描述这组数据的离散程度，并把S2叫做这组数据的方差。

知识点6：标准差方差的算术平方根，即用S=来描述这一组数据的离散程度，并把它叫做这组数据的标准差。

知识点7：方差与平均数的性质若x1，x2，…x n的方差是S2，平均数是，则有①x1+b，x2+b…x n+b的方差为S2，平均数是+b②ax1，ax2，…ax n的方差为a2s2，平均数是a③ax1+b，ax2+b，…ax n+b的方差为a2s2，平均数是a+b同步练习：1为了从甲、乙两名学生中选拔一人参加电脑知识竞赛，在相同条件下对他的电脑知识进行了10次测试，成绩如下：（单位：分）甲的成绩76849086818786828583乙的成绩82848589798091897479回答下列问题：（1）甲学生成绩的众数是分，乙学生成绩的中位数是分。

（2）若甲学生成绩的平均数为，乙学生成绩的平均数为，则与的大小关系是。

（3）经计算知=13.2，=26.36，这说明。

初中数学知识归纳统计数据的集中趋势和离散程度统计学是一门研究数据收集、处理、分析和解释的学科，它在生活中的应用非常广泛。

在统计学中，我们常常需要描述数据的集中趋势和离散程度。

本文将介绍几种常见的数据集中趋势和离散程度的统计量以及它们的含义和计算方法。

一、数据的集中趋势数据的集中趋势是指一组数据向某个中心值靠拢的趋势。

常用的统计量有均值、中位数和众数。

1. 均值（Mean）均值是指一组数据的总和除以数据的个数。

它是最常用的集中趋势统计量，用于表示数据的平均水平。

计算均值的方法是将所有数据相加，然后除以数据的个数。

2. 中位数（Median）中位数是指一组数据中处于中间位置的值。

当数据集的个数为奇数时，中位数就是数据排序后的中间值；当数据集的个数为偶数时，中位数是中间两个数的平均值。

计算中位数的方法是将数据从小到大排序，然后找到中间位置的值。

3. 众数（Mode）众数是指一组数据中出现次数最多的数值。

一个数据集可能有一个或多个众数，也可能没有众数。

计算众数的方法是统计每个数值出现的频数，然后找到频数最大的数值。

二、数据的离散程度数据的离散程度是指一组数据的分散程度或波动程度。

常用的统计量有极差和标准差。

1. 极差（Range）极差是指一组数据的最大值与最小值之间的差值。

它是最简单的离散程度统计量，可以直观地反映数据的变化范围。

计算极差的方法是将最大值减去最小值。

2. 标准差（Standard Deviation）标准差是指一组数据偏离平均值的程度。

它通过计算每个数据与均值的差的平方，并求平均值来衡量数据的离散程度。

标准差越大，数据的离散程度越大。

计算标准差的方法包括计算均值、计算每个数据与均值的差的平方，并求平均值再开方。

三、应用举例现在我们来举两个实际问题的例子，通过计算集中趋势和离散程度的统计量来分析数据。

例1：小明的五次数学考试成绩分别是85、92、88、79和90，求这五次考试成绩的均值、中位数、众数、极差和标准差。

知识点数据的中心趋势与离散程度在数据分析中，了解和解释数据的中心趋势和离散程度是非常重要的。

知识点数据的中心趋势和离散程度是指用来表示一组数据的平均值、中位数和众数等统计指标，以及表达数据分布的方差和标准差等指标。

通过对数据的中心趋势和离散程度的分析，可以更好地理解数据的特点和规律。

一、数据的中心趋势数据的中心趋势是用来描述数据集中值的指标。

常见的中心趋势有平均数、中位数和众数。

1. 平均数（Mean）平均数是指将所有数据求和后除以数据的个数，它代表了数据的均衡状态。

平均数是表征数据总体的重要指标，但受离群值的影响较大，因此在某些情况下需要谨慎使用。

2. 中位数（Median）中位数是将一组数据按照从小到大的顺序排列后，位于中间位置的值，它不受极端值的影响，更能反映数据的中心趋势。

如果数据个数为奇数，则中位数正好是中间的那个值；如果数据个数为偶数，则中位数是中间两个值的平均数。

3. 众数（Mode）众数是指在一组数据中出现次数最多的数值，它可以反映数据的重复程度。

一个数据集可以有一个或多个众数，甚至可以没有众数。

二、数据的离散程度数据的离散程度是用来描述数据分布的指标。

常见的离散程度有极差、方差和标准差。

1. 极差（Range）极差是一组数据的最大值与最小值之差，它可以反映数据的变化范围。

然而，极差只考虑了两个极端值，没有考虑整个数据集的分布情况，因此它的描述能力较弱。

2. 方差（Variance）方差是数据与其平均数之间差异的平方和的平均数，它衡量了数据与平均数的偏离程度。

方差越大，表示数据分布的离散程度越高；方差越小，则表示数据分布越集中。

3. 标准差（Standard Deviation）标准差是方差的非负平方根，它与方差具有相同的度量单位，但更易于理解和解释。

标准差是用来描述数据集中个体差异的指标，标准差越大，表示个体差异越大，离散程度越高。

总结而言，数据的中心趋势和离散程度是用来描述和分析数据的基本统计特征的指标。

理解数据的集中趋势与离散程度数据在现代社会中扮演着重要的角色，无论是科学研究、商业决策还是社会分析，都离不开数据的支持。

然而，仅仅拥有大量的数据还不足以使我们做出准确的判断和决策，我们还需要理解数据的集中趋势与离散程度。

本文将探讨如何理解数据的集中趋势与离散程度，并介绍一些常用的统计指标和方法。

一、集中趋势集中趋势是用来描述数据的中心位置的统计指标。

常用的集中趋势指标有平均数、中位数和众数。

平均数是最常见的集中趋势指标，它是一组数据的总和除以数据的个数。

平均数可以反映数据的总体水平，但在存在离群值的情况下，平均数可能会被拉偏。

中位数是将一组数据按照大小顺序排列后，位于中间位置的数值。

中位数不受离群值的影响，更能反映数据的典型特征。

众数是一组数据中出现频率最高的数值。

众数常用于描述离散型数据的集中趋势，如衣服尺码、颜色等。

二、离散程度离散程度是用来描述数据的分散程度的统计指标。

常用的离散程度指标有极差、方差和标准差。

极差是一组数据的最大值与最小值之间的差异。

极差越大，数据的离散程度越大。

方差是一组数据与其平均数之差的平方和的平均数。

方差可以衡量数据的离散程度，值越大表示数据越分散。

标准差是方差的平方根，它和方差具有相同的度量单位。

标准差是最常用的衡量数据离散程度的指标，它能够直观地反映数据的离散程度。

三、常用的统计方法除了上述的指标外，还有一些常用的统计方法可以帮助我们更好地理解数据的集中趋势与离散程度。

箱线图是一种常用的可视化方法，它能够直观地展示数据的集中趋势和离散程度。

箱线图由一个箱体和两条线组成，箱体表示数据的四分位数，上下两条线表示数据的最大值和最小值，异常值可以通过箱线图来观察和判断。

正态分布是一种常见的概率分布，它的均值和标准差可以完全描述数据的集中趋势和离散程度。

通过正态分布的偏度和峰度指标，我们可以判断数据是否符合正态分布。

回归分析是一种常用的统计方法，它可以帮助我们建立数据的数学模型，进而预测和解释数据的集中趋势和离散程度。

数据的集中趋势和离散程度笔记一、知识点梳理知识点1：表示数据集中趋势的代表平均数、众数、中位数都是描述一组数据集中趋势的特征数，只是描述的角度不同，其中平均数的应用最为广泛。

（1）平均数算术平均数（简称为平均数）：121()n xx x x n（公式一）①一般地，如果在一组数据中，x 1出现f 1次，x 2出现f 2次，……，x k 出现f k 次，（f 1，f 2，…f k 为正整数），则这组数据的平均数：当n 个数据中某些数据反复出现时，用该公式较简洁； f 1+f 2+…+f k =n （数据的总个数）。

②一般地，如果一组数据都在某个数a 上下波动时，就可以采用把原来每个数据都减去a ，得一组新数据，再算得这组新数据的平均数'x ，这样原来数据的平均数是：x ＝a ＋'x （公式三）平均数定义公式和两个简化计算公式都很重要，应根据具体情况，恰当选用。

特别的：一组数据x 1，x 2，…，x n 的平均数为x ，①若每个数据都扩大a 倍，即ax 1，ax 2，…，ax n ，则平均数也扩大a 倍，即a x ； ②若每个数据都增加b ，即x 1＋b ，x 2＋b ，…，x n ＋b ，则平均数增加b ，即x ＋b ； ③若每个数据都扩大a 倍后又都增加b ，则平均数也扩大a 倍后增加b ，即a x ＋b ． 当数据组中数据较大又在某个数值左右波动或数据之间存在某种倍数关系时，利用这些规律求平均数比较直接、简便。

加权平均数在计算数据的平均数时，往往根据其重要程度，分别给每个数据一个“权”，由此求出平均数叫做加权平均数。

恒量各个数据“重要程度”的数值叫做权。

相同数据的个数叫做权，这个“权”含有所占分量轻重的意思。

ω1越大，表示x 1的个数越多，于是x 1的“权”就越重。

若n 个数x 1，x 2，…，x n 的权是分别是ω1，ω2，…，ωn ，则x ＝nnn x x x ωωωωωω++++++ 212211① 当ω1＝ω2＝…＝ωn ，即各项的权相等时，加权平均数就是算术平均数。

数据的集中趋势与离散程度数据在现代社会中扮演着重要的角色，它们不仅可以揭示事物的本质和规律，还可以为决策提供支持。

在数据分析中，我们经常会关注数据的集中趋势和离散程度，这些指标能够帮助我们更好地理解数据的特征和分布。

本文将探讨数据的集中趋势和离散程度，并介绍一些常用的统计量和方法。

一、集中趋势集中趋势是描述数据分布中心位置的指标，它能够反映数据的平均水平。

常见的集中趋势统计量有均值、中位数和众数。

均值是数据的算术平均值，它是将所有数据相加后再除以数据个数得到的结果。

均值能够反映数据的总体水平，但受极端值的影响较大。

例如，一个班级的学生年龄平均值是15岁，但如果班级中有一个20岁的学生，那么平均值就会被拉高。

因此，在计算均值时需要注意数据的分布情况。

中位数是将数据按大小顺序排列后，位于中间位置的数值。

中位数能够较好地反映数据的中心位置，不受极端值的影响。

例如，一个班级的学生年龄中位数是14岁，即有一半学生的年龄小于等于14岁，另一半学生的年龄大于等于14岁。

众数是数据中出现次数最多的数值。

众数能够反映数据中的典型值，但可能存在多个众数或无众数的情况。

例如，一个班级的学生身高众数是160cm，即身高为160cm的学生最多。

二、离散程度离散程度是描述数据分布的分散程度的指标，它能够反映数据的波动情况。

常见的离散程度统计量有范围、方差和标准差。

范围是数据的最大值与最小值之间的差异。

范围能够简单地反映数据的离散程度，但容易受极端值的影响。

例如，一个班级的学生成绩范围是60分到100分，范围为40分，但如果有一个学生得了0分或者满分150分，范围就会变得不够准确。

方差是数据与均值之间差异的平方的平均值。

方差能够较好地反映数据的离散程度，但计算过程较为繁琐。

方差越大，数据的离散程度越高。

例如，一个班级的学生成绩方差为100，说明学生成绩波动较大。

标准差是方差的平方根，它与方差具有相同的度量单位。

标准差能够在方差的基础上更好地理解数据的离散程度。