当前位置：文档之家 › 工程力学第三章 受力分析(课堂PPT)

工程力学第三章 受力分析(课堂PPT)

  • 格式：ppt
  • 大小：2.03 MB
  • 文档页数：42

下载文档原格式

  / 42

合集下载

结构力学 -受力分析PPT教学课件

结构力学 -受力分析PPT教学课件
A
FAy
a1
Bx
FBy
若约束反力 FAy 、FBy 已求得， 用截面法可以求梁指定横截 面 I—I 上的内力 ：
Fy 0 qa FSy FAy 0
FSy FAy qa
A
qa q FSy
FAy
a C Mz
剪力为该截面一侧横向力的代数和
MC 0
a
M Z qa 2 FAy a 0
第三章 静定结构受力分析
2020/12/10
1
静定结构受力分析
几何特性：无多余联系的几何不变体系 静力特征：仅由静力平衡条件可求全部反力内力 求解一般原则：从几何组成入手，按组成的相反
顺序进行逐步分析即可 本章内容：
静定梁；静定刚架；静定桁架；静定组合结构； 平面薄壁结构；空间薄壁结构 学习中应注意的问题：多思考,勤动手。本章是后面 学习的基础，十分重要，要熟练掌握！
2020/12/10
2
§3-1 静定梁受力分析
一.单跨梁
1.单跨梁支反力
例.求图示粱支反力
A Fp FAx
解:
FX 0 FAx 0
B
FY 0 FBy F p()M2020/12/10
L/2 L/2 FBy
M A 0 M Fp L / 2( )
3
2.截面法求指定截面内力
剪力与弯矩
q1
MZ
FAya
qa2 2
2020/12/10
弯矩为该截面一侧横向力对截面中心力矩的代数和4
2020/12/10
5

03结构简图和物体受力分析(工程力学基础)

03结构简图和物体受力分析(工程力学基础)

四、支座的简化
1、支座简化示例 固定铰支座、可动铰支座、固定端支座、定向支座等都是理想的支 座。为便于计算，要分析实际结构支座的主要约束功能与哪种理想 支座的约束功能相符合，将工程结构的实际支座简化为力学中的理 想支座。 图（a）中所示的是预制钢筋混凝土柱与杯形基础的连接形式。基 础下面是比较坚实的地基，如杯口四周填人沥青麻丝，荷载的作用 能使柱端发生微小转动，其约束功能基本上与固定铰支座相符合， 则可简化为固定铰支座，如图（b）所示。如将预制钢筋混凝土柱插 在较深的杯形基础中，杯口四周及底部用细石混凝土填实，如图（c ）所示，柱端被相当坚实地固定住，其约束功能基本上与固定支座 相符合，则可简化为固定端支座，如图（d）所示。
位移的条件。
5
§3-2 平面体系的几何组成分析
１、几何可变体系：在荷载作用下 不能保持其几何形状和位置都不改 变的体系。
２、几何不变体系：在荷载作用下 能保持其几何形状和位置都不改变 的体系。
3、刚片 平面内的刚体称为刚片 4、自由度 体系可独立运动的方式称为该体系的自由度。
或表示体系位置的独立坐标数。 平面体系的自由度：用以确定平面体系在平面
六、计算跨度
计算简图的选取案例
七、平面杆系结构的分类
（一）按结构形式分
（1）梁式结构 ：梁由受弯杆件构成，杆件轴线一般为直线。 （2）刚架结构 ： 刚架是由梁和柱组成的结构。 （3）桁架结构 ： 桁架是由若干直杆在两端用铰链连接组成的结
构。。 （4）拱结构 ： 拱一般由曲杆构成。 （5）组合结构： 组合结构是桁架和梁或刚架组合在一起形成的
两刚片规则例
规则二：三刚片规则
三个刚片用不全在一条直线上的 三个单铰（可以是虚铰）两两相 连，组成无多余约束的几何不变 体系。如图所示。 铰接三角形规则：简称三角形规 则

工程力学：第三章 空间问题的受力分析

工程力学：第三章 空间问题的受力分析

。CDB平面与水平
面间的夹角
，物重
。如起重杆的重量不计，试求
起重杆所受的压力和绳子的拉力。
解：取起重杆AB与 重物为研究对象。
取坐标轴如图所示。 由已知条件知：
列平衡方程 解得
§3-3 力对轴的矩 力F对z轴的矩就是分力Fxy 对点O的矩， 即
力对轴的矩是力使刚体绕该 轴转动效果的度量、是一个 代数量。
空间力偶系平衡的必要和充分条件是：该力偶系的合力偶矩等 于零，亦即所有力偶矩矢的矢量和等于零，即
由上式，有 欲使上式成立，必须同时满足
空间力偶系未知量）
空间力偶系平衡的必要和充分条件为：该力偶系中所有各力偶 矩矢在三个坐标轴上投影的代数和分别等于零。
§3-5 空间任意力系的平衡方程
可将上述条件写成空间任意力系的平衡方程
注：1.与平面力系相同，空间力系的平衡方程也有其它的形式。 2.六个独立的平衡方程，求解六个未知量。 3.可以从空间任意力系的普遍平衡规律中导出特殊情况的 平衡规律，例如空间平行力系、空间汇交力系和平面任意 力系等平衡方程。
例：设物体受一空间平行力系作用。 令z轴与这些力平行，则
绝对值： 该力在垂直于该轴的平面上的投影对于 这个平面与该轴的交点的矩的大小。
正负号： 从z轴正端来看，若力的这个投影使物体绕该轴 按逆时针转向转动，则取正号，反之取负号。
也可按右手螺旋规则来确定其正负号，如图所 示，姆指指向与z轴一致为正，反之为负。
当力与轴在同一平面时，力对该轴的矩等于零：
(1)当力与轴相交时 (此时h＝0)；
（三个方程，可 求解三个未知量）
空间汇交力系平衡的必要和充分条件为：该力系中所有各力 在三个坐标轴上的投影的代数和分别等于零。

第三章静定结构的受力分析PPT课件

第三章静定结构的受力分析PPT课件

A
点、集中力偶作用点、分布荷载作用点的起点 FQA
和终点等）为控制界面
MA
⑵ 在两控制截面弯矩值作出的虚线上，
叠加该段简支梁作用荷载时产生的弯矩值。
A
七、简易法作内力图
q
l
q l2 8
MB B
FQB
MB B
利用微分关系定形，利用特殊点的内力值来定值或利用积分关系定值。
基本步骤： 1、确定梁上所有外力（求支座反力）； 2、分段 3、利用微分规律判断梁各段内力图的形状； 4、确定控制点内力的数值大小及正负； 5、画内力图。
剪力 — 截面上应力沿杆轴法线方 向的合力, 使杆微段有顺时针方向转动 趋势的为正，画剪力图要注明正负号。
M
M
二、计算截面内力的截面法
弯矩 — 截面上应力对截面形心的 力矩之和。在水平杆件中，当弯矩使杆 件下部受拉时，弯矩为正。弯矩图画在 杆件受拉一侧，不注符号。
⑴ 先求支座反力（悬臂结构除外）
⑵ 将拟求内力的截面断开，选取外力少的部分作隔离体受力图。
m 2
2、力偶作用点 M图有一突变，力矩 为顺时针向下突变； F Q 图没有变化。
五、内力图形状特征
l
ql 2
ql 2
q 8
3、均布荷载作用段 M图为抛物线，荷载向 下曲线亦向下凸； F Q 图为斜直线，荷载向 下直线由左向右下斜
7
1、在自由端、铰支座、铰结点处，无集中力偶作用，截面弯矩等于零，有 集中力偶作用，截面弯矩等于集中力偶的值。
2、刚结点上各杆端弯矩及集中力偶应满足结点的力矩平衡。两杆相交刚结 点无 m 作用时，两杆端弯矩等值，同侧受拉。
3、具有定向连结的杆端剪力等于零，如无横向荷载作用，该端弯矩为零。

第3章 平面静定结构受力分析(17)

第3章 平面静定结构受力分析(17)

第三章平面静定结构受力分析静定结构受力分析之歌内力分析要提升，等效截面法冲锋。

内力标记有新规，杆段截面都分明。

剪力轴力与前无异，弯矩顺时针恒正。

受力图上力已知，叠加绘图分分钟。

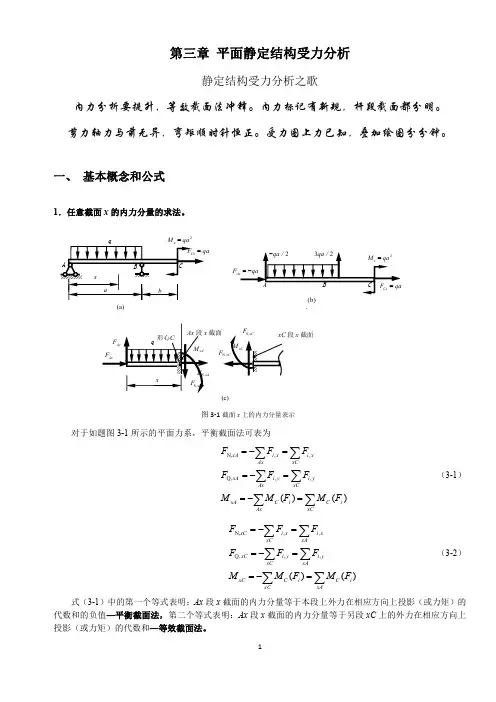
一、基本概念和公式1．任意截面x 的内力分量的求法。

图3-1截面x 上的内力分量表示段x 截面(a)(b)2q(c)32qa /2qa /-2e M qa =Cx F qa=Ax F qa=-AB C对于如题图3-1所示的平面力系，平衡截面法可表为N,,,Q,,,()()xA i x i xAxxCxA i y i yAxxCxA C i C i AxxCF F F F F F M M F M F =-==-==-=∑∑∑∑∑∑（3-1）N,,,Q,,,()()xC i x i xxCxAxC i y i yxCxAxC C i C i xCxAF F F F F F M M F M F =-==-==-=∑∑∑∑∑∑（3-2）式（3-1）中的第一个等式表明：Ax 段x 截面的内力分量等于本段上外力在相应方向上投影（或力矩）的代数和的负值—平衡截面法，第二个等式表明：Ax 段x 截面的内力分量等于另段xC 上的外力在相应方向上投影（或力矩）的代数和—等效截面法。

式（3-2）第一个等式表明：xC 段x 截面的内力分量等于本段上外力在相应方向上投影（或关于截面形心C 的力矩）的代数和的负值—平衡截面法，第二个等式表明：xC 段x 截面的内力分量等于另段Ax 上的外力在相应方向上投影（或力矩）的代数和—等效截面法。

式（3-1）的第二个等式更深刻和具体的表述为：Ax 段x 截面的内力的主矢和主矩等于xC 段上所有外力关于x 截面形心的主矢和主矩。

用内力分量表示就是：（1）Ax 段x 截面的轴力N,xA F 等于xC 段上所有外力在轴线方向投影的代数和；（2）剪力Q,xA F 等于xC 段上所有外力在竖直方向投影的代数和；（3）弯矩xA M 等于xC 段上所有外力关于x 截面形心的力矩的代数和。

人教版必修1 第三章相互作用专题-受力分析(共14张PPT)

人教版必修1 第三章相互作用专题-受力分析(共14张PPT)

F
G f1’ G
f4 f3
f2
f1
G
G f3’
f2’G
f1’ G
T
N
T＇
f
G1
N1
T
G2
N2
G G
N2 N1
球光滑
G
F3 N1’ G
F4 G N2’
光
滑
圆
F
环
N G
N
F f
G
向上运动趋势
N F
G 无运动趋势
N
f
F
G
向下运动趋势
N
f G
向上运动趋势
N
G 无运动趋势
N
f
G 向下运动趋势
T
T
对结点O
F＇ F＇
N
F
F
G1
G2
《皮带传动中的摩擦力》
A
V
B
E¨F
P¨Q
A为从动轮，B为驱动轮，且皮带不打滑。
试判断：
驱动轮与皮带接触处P、Q两点静摩擦力方向？ 从动轮与皮带接触处F、E两点静摩擦力方向？
《自行车运动中前后轮与地面接触处的摩擦力》 1、推车行走？ 2、骑车前进？
再好的种子，不播种下去，也结不出丰硕的果实 到用时方恨少，事非经过不知难。竹笋虽然柔嫩 它不怕重压，敢于奋斗、敢于冒尖。少壮不努力 大徒伤悲。天行健，君子以自强不息不向前走， 路远；不努力学习，不明白真理。用习惯和智慧 奇迹，用理想和信心换取动力天才在于积累，聪 于勤奋。奋斗之路越曲折，心灵越纯洁。人必须 耐心，特别是要有信心。努力向上的开拓，才使 的竹鞭化作了笔直的毛竹。不要让追求之舟停泊 想的港湾，而扬起奋斗的风帆，驶向现实生活的 习惯决定成绩，细节决定命运。良好的习惯是成 保证。逆境是磨练人的最高学府。生命力顽强的 从不对瘠土唱诅咒的歌。一个能思考的人，才真 个力量无边的人。耕耘者的汗水是哺育种子成长

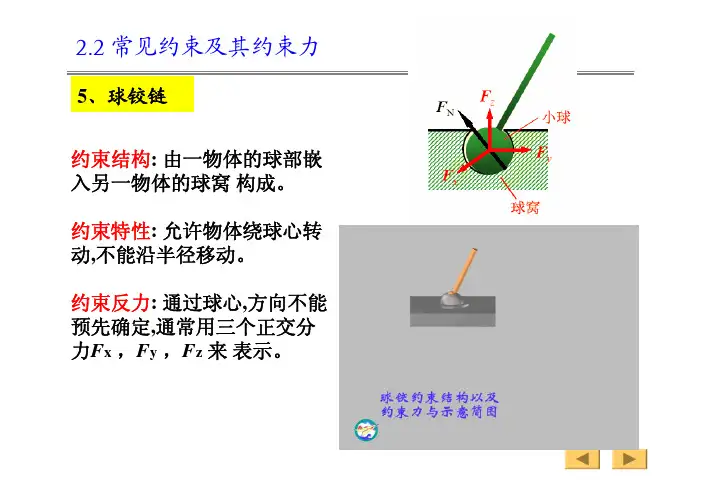
理论力学课件 受力分析与受力图、第三章

理论力学课件 受力分析与受力图、第三章

5、球铰链
约束结构: 由一物体的球部嵌入另一物体的球窝构成。

约束特性: 允许物体绕球心转动,不能沿半径移动。

约束反力: 通过球心,方向不能预先确定,通常用三个正交分力F x，F y，F z来表示。

人造髋关节
二力杆工程实例
固定端约束除了加约束力，还要加上约束力偶。

运动学角度：固定端既限制线位移，又限制角位移，如果只有约束力，则构件将转动。

必须有约束力偶才行。

力系简化角度：固定端所受的力是一个复杂的平面任意力系，力系向端部某点简化的结果是一力和一力偶。

CD是不是二力
杆？
2.3 受力分析与受力图
刚化原理：若变形体在某一力系作用下处于平衡，则将此变形体刚化为刚体，其平衡状态保持不变。

只有刚化原理没有软化原理。

1. 右拱BC 的受力图。

C
B
解：
F C
F B
2. 左拱AC 的受力图。

A C
F
F Ax C F
F Ay。

工程力学第三章 物体的受力分析结构的计算简图

工程力学第三章 物体的受力分析结构的计算简图
所示
系统整体受力图如图（d） 所示
§3–2物体的受力分析及受力图
考虑到左拱 AC 在三个力 作用下平衡，也可按三力平 衡汇交定理画出左拱AC 的 受力图，如图（e）所示
此时整体受力图如图（f） 所示
§3–2物体的受力分析及受力图
例1－5
不计自重的梯子放在光滑 水平地面上，画出绳子、 梯子左右两部分与整个系 统受力图。图(a)
杆的受力图能否画为 图（d）所示？
若这样画，梁AB的受力 图又如何改动?
§3–2物体的受力分析及受力图
例1-4
不计三铰拱桥的自重与摩擦，画 出左、右拱AC,CB的受力图与系 统整体受力图。
解： 右拱CB为二力构件，其受力 图如图（b）所示
§3–2物体的受力分析及受力图
取左拱AC ,其受力图如图（c）
可用二个通过轴心的正交分力Fx, Fy 表
示。
（2） 、光滑圆柱铰链
约束特点：由两个各穿孔的构件及圆柱销钉 组成，如剪刀。
§3–1约束与约束反力
§3–1约束与约束反力
光滑圆柱铰链：亦为孔与轴的配合问题， 与轴承一样，可用两个正交分力表示。
其中有作用反作用关系
Fcx Fcx, Fcy Fcy
解：画出简图 画出主动力
画出约束力
§3–2物体的受力分析及受力图
例1-3
水平均质梁AB重为 P1，电动机重
为 P2，不计杆 CD 的自重，画出杆
P2
CD和梁 AB的受力图。图(a)
解： 取 CD 杆，其为二力构件， 简称二力杆，其受力图如图 (b)
§3–2物体的受力分析及受力图
取AB梁，其受力图如图 (c)
（4）定向支座（滑动铰支座）
§3–1约束与约束反力

工程力学第三章课件

工程力学第三章课件

(F
)
0
附加条件：x（或 y）轴不能垂直于 AB 连线。
三矩式：
M M
A B
(F (F
) )
0 0
MC (F ) 0
附加条件：A，B，C 不在同一直线上。
上式是物体取得平衡的必要条件，但不是充分条件，必 须加上附加条件后，才能成为物体平衡的充分必要条件。
3.3.1 平面任意力系的平衡条件和平衡方程
（1） FR 0，MO 0 ； （3） FR 0，MO 0 ；
（2） FR 0，MO 0 ； （4） FR 0，MO 0 。
3.2.1 平面任意力系简化为一个力偶的情形
如果力系的主矢等于零，而力系对于简化中心的主矩不等于零，则原力系向简化中心等效 平移后的汇交力系已自行平衡，只剩下附加力偶系。
MO (F ) 0
平面任意力系的平衡方程
平面任意力系平衡的解析条件为：所 有各力在两任选坐标轴上的投影的代数 和分别等于零，各力对于任意一点的矩 的件和平衡方程
平面任意力系的平衡方程还有另外两种形式：
二矩式：
Fx M
0 A (F
)
0
M
B
3.2.3 平面任意力系平衡的情形
如果力系的主矢、主矩都等于零，即 FR 0，MO 0 ，则原力系平衡。
03
平面任意力系的平衡方程
3.3.1 平面任意力系的平衡条件和平衡方程
平面任意力系平衡的充要条件是：力系的主矢和对任一点的主矩都为零，即
F R MO
0 0
Fx 0 上述平衡条件也可用解析式表达如下： Fy 0
3.1.1 力的平移定理
力的平移定理：
证明：如图所示，刚体上作用有力 F。在刚体上任取一点 B，并在点 B 加上一对平衡力系 F′和 F′′， 令 F F F 。由静力学公理 3 可知，这三个力与原来的力 F 等效，同时这三个力又可以看成是作

大学物理 力学-受力分析

大学物理 力学-受力分析
力系对刚体的作用。 推论1：力的可传性
作用于刚体上的力，可沿其作用线移到同一刚体内的任 一点，而不改变该力对刚体的效应。
因此，对刚体来说，力作用三要素为：大小，方向，作用线。
12
公理3 力的平行四边形法则 作用在物体上同一点的两个力，可合
成为一个合力。此合力也作用于该点，合 力的大小和方向，由这两力矢为邻边所构 成的平行四边形的对角线确定。
工程力学主要研究物体的机械运动和杆件弹性变形的一般规 律。它是高等工科院校的一门理论性较强的技术基础课程，为后 续课程的学习和解决工程实际问题提供力学的基本理论和方法。
机械设备或工程结构都是由若干构件组成的。当它们传递 运动或承受载荷时，各个构件都要受到力的作用。因此，首先必 须确定有哪些力在作用各个构件上，以及它们的大小和方向；其 次还必须为构件选用合适的材料，确定合理的截面形状和尺寸， 以保证构件既能安全可靠的工作又符合经济要求。这些都是工程 力学所要解决的问题。
R F1 F2
推论2：三力平衡汇交定理
刚体受三力作用而平衡，若其中两力
作用线汇交于一点，则另一力的作用线必
汇交于同一点，且三力的作用线共面。
（必共面，在特殊情况下，力在无穷远
处汇交——平行力系。）
13
[证] ∵ F1 , F2 , F3为平衡力系， ∴ R , F3 也为平衡力系。
又∵ 二力平衡必等值、反向、共线，
即受力图一定要画在分离体上。
38
5.受力图上只画外力，不画内力 一个力，属于外力还是内力，因研究对象的不同，有
可能不同。当物体系统拆开来分析时，原系统的部分内力， 就成为新研究对象的外力。
6.同一系统各研究对象的受力图必须整体与局部一致，相 互协调，不能相互矛盾 对于某一处的约束反力的方向一旦设定，在整体、局部
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
31
解：
1.杆AB的受力图。
2. 活塞和连杆的受力图。
E D
B
Aq
C q
B
FBA
A
FA
3. 压块 C 的受力图。
q
FCB
FAB
q
C FCx
F
B
q
FBC
1 FCy
32
例题7
D
A
K
q
C
E
BⅠ Ⅱ
P
如图所示平面构架，由杆AB ， DE及DB铰接而成。钢绳一端拴 在K处，另一端绕过定滑轮Ⅰ和 动滑轮Ⅱ后拴在销钉B上。重物 的重量为P，各杆和滑轮的自重 不计。（1）试分别画出各杆， 各滑轮，销钉B以及整个系统的 受力图；（2）画出销钉B与滑轮 Ⅰ一起的受力图；（3）画出杆 AB ，滑轮Ⅰ ，Ⅱ ，钢绳和重物 作为一个系统时的受力图
处必有力，力的方向由约束类型而定。
要注意力是物体之间的相互机械作用。因此对 2、不要多画力 于受力体所受的每一个力，都应能明确地指出
它是哪一个施力体施加的。
1
18
3、不要画错力的方向 约束反力的方向必须严格地按照约束的类型来画，不 能单凭直观或根据主动力的方向来简单推想。在分析 两物体之间的作用力与反作用力时，要注意，作用力 的方向一旦确定，反作用力的方向一定要与之相反， 不要把箭头方向画错。
BB
D
F
A
C
1
7
解： 1. 杆 BC 的受力图。
BB
D
F
A
C
1
FB B
C
FC
8
2. 杆AB 的受力图。
BB
D
F
A
正交分解
FB
B
FD
C
FAy
A
FAx
第一种画法
1
三力平衡汇交
FB
B D
H
F
A
FA
第二种画法
9
例4
A
F
H
D
E
B
C
如图所示，梯子的两部分 AB和AC在A点铰接，又在 D ，E两点用水平绳连接。 梯子放在光滑水平面上， 若其自重不计，但在AB的 中点处作用一铅直载荷F。 试分别画出梯子的AB，AC 部分以及整个系统的受力 图。
E
A F
q
P1
HG C
D B
P2
1
ห้องสมุดไป่ตู้
29
例 题 4 解：
1.物块 B 的受力图。
2. 球A 的受力图。
FE E
FD D B
P2
E
A F
q
P1
HG C
D B
P2
A F
P1 FF
I H
FH
G
C
FC
FG
1
3.滑轮 C 的受力3图0 。
例题6
E D
B
Aq
C q
如图所示压榨机中，杆AB 和BC的长度相等，自重忽略 不计。A ，B，C ，E处为铰 链连接。已知活塞D上受到油 缸内的总压力为F 。试画出 杆AB ，活塞和连杆以及压块 C的受力图。
7 、正确判断二力构件
1
20
物体的受力分析
PF
C
A
如图所示的三铰拱 桥，由左右两拱桥铰接 而成。设各拱桥的自重 不计，在拱上作用有载
B
荷F，试分别画出左拱 和右拱的受力图。
1
21
解：
1. 右拱 BC 的受力图。
FC
P
A
B
FC
C
B FB
1
22
2. 左拱 AC 的受力图。
F
表示法一
F
D
C
FC
A
FA
NBx
1
NBy
N’cy
N’cx
14
[例6] 画出下列各构件的受力图
1
15
尖点问题
应去掉约束
应去掉约束
1
16
[例7] 画出下列各构件的受力图
1
17
三、画受力图应注意的问题
1、不要漏画力
除主动力外，只要物体相互接触，就一定存 在有机械作用。要分清研究对象（受力体）
都与周围哪些物体（施力体）相接触，接触
F
A P
B
1
27
例 题3
F
解：
碾子的受力图为:
F
A P B
P
A B
FNA
FNB
1
28
例 题4
在图示的平面系统中，匀质 球A 重P1，本身重量和摩擦不计 的理想滑轮C 和柔绳维持在仰角
是q 的光滑斜面上，绳的一端挂
着重P2的物块B。试分析物块B , 球A和滑轮C的受力情况，并分 别画出平衡时各物体的受力图。
24
解： 1.杆AB的受力图。
A
FAB
A
60
D
B
2.杆BC 的受力图。
FBC
30
B
G
C
FCB1
C
B
FBA
25
A
60
D
30
C
3. 滑轮B ( 不带
销钉）的受力图。
B
FBy
F2
D
FBx
G
F1
4. 滑轮B ( 带销 钉）的受力图。
F2
FBA
B
30
60
FBC
F1
1
26
例 题3
用力F 拉动碾子以轧平路面,重为P 的碾子 受到一石块的阻碍，如图所示。试画出碾子的受 力图。
内容回顾
约束的基本类型和约束反力的特点
1.柔性约束 2.光滑面约束 3.光滑铰链约束
①圆柱形销钉连接 ②固定铰支座 ③活动（可动）铰支座（辊轴支座）
1
1
本次课主要内容
• 教学内容： 物体的受力分析、受力图
• 教学目标：
熟练掌握物体受力分析和画受力图的方法。
1
2
§1-4 物体的受力分析和受力图
一、受力分析 无论是研究物体的平衡还是研究物体的运动规律，
4、受力图上不能再带约束。
即受力图一定要画在分离体上。
1
19
5、受力图上只画外力，不画内力。 一个力，属于外力还是内力，因研究对象的不同，有 可能不同。当物体系统拆开来分析时，原系统的部分 内力，就成为新研究对象的外力。
6 、同一系统各研究对象的受力图必须整体与局部一致，相 互协调，不能相互矛盾。 对于某一处的约束反力的方向一旦设定，在整体、局 部或单个物体的受力图上要与之保持一致。
N1 C
N2 A
P
XA
YA
画约束反力时，一定要按照约束的固有性质画图，
切不可主观臆断！
1
5
例2 画出图中球O与杆AB的受力分析图
1
6
例3
等腰三角形构架ABC 的顶点 A，B，C 都用铰链连接，底边 AC固定，而AB 边的中点D 作用 有平行于固定边AC 的力F，如图 所示。不计各杆自重，试画出杆 AB 和BC 的受力图。
1
10
F
H D B
解： 1.梯子AB 部分的受力图。
FAy
A
FA
FAx
H
E
FB
FD
D
C B
2.梯子AC 部分的受力图。
1
FAx
A
FAy
FC
FE
E
C
11
3.梯子整体的受力图。
A
F
H
D
E
B
C
F
A
H
FB
D B
FC
E C
1
12
[例5] 画出下列各构件的受力图
O
C
E
D
Q
A
B
1
13
O
C
E
D
Q
A
B
Ncx Ncy
F
FAx A FAy
1表示法二
C
FC
23
例题2
A
60
D
B
30
G C
如图所示，重物重G = 20 kN, 用钢丝绳挂在支架的滑轮B上，钢 丝绳的另一端绕在铰车D上。杆AB 与BC铰接，并以铰链A，C与墙连 接。如两杆与滑轮的自重不计并忽 略摩擦和滑轮的大小，试画出杆AB 和BC以及滑轮B的受力图。
1
都需要分析物体的受力情况。
1.分离体（研究对象）
2.受力分析
3.受力图
作用在物体上的力有：主动力,被动力(约束反力)。
1
3
二、受力分析的步骤
① 取研究对象；
② 取分离体；
③ 画上主动力；
④ 找接触点或连接点；
⑤ 画出约束反力。
1
4
例1 画出图中的球和杆AB的受力分析图
解： B P
B
SBC N2
600 A