当前位置：文档之家 › 第三章 多组分精馏

第三章 多组分精馏

  • 格式：doc
  • 大小：123.50 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

第3章多组分精馏

第3章多组分精馏
1、溶剂的稀释作用：当被分离物系的非理想性较大， 且在一定浓度范围难以分离时，加入溶剂→原有组分 浓度均下降→减弱了它们之间的相互作用，只要溶剂 浓度足够大，就可突出两组分挥发度的差异。
2、溶剂的选择性：当原有两组分 A和B的沸点相近， 非理想性不大，加入溶剂后，溶剂与A形成具有较强 正偏差的非理想溶液，与B 形成负偏差溶液或理想溶 液，从而提高了A对B的相对挥发度。溶剂的作用在 于对不同组分相互作用的强弱有较大差异。
在同样压力下，共沸精馏的操作温度通常比萃取精 馏低，故共沸精馏更适用于分离热敏性物料；
共沸精馏可连续操作，也可间歇操作，萃取精馏一 般只能连续操作。
2021年6月
9
二、特殊精馏简介
3、反应精馏
1）加入C物质，使之与原体系中的A发生反应，从 而削弱A与B的结合力。
通过反应强化分离
2）反应与分离在塔内同时进行，生产另一种物质 的过程-耦合技术。如乙醇、乙酸反应生成乙酸乙 酯与水，是可逆反应。在塔内反应的同时，将产物 从塔顶采出，提高了反应转化率。
25
一、萃取精馏流程
溶剂的加入位置： 1）若加料混合物是最低 恒沸物，一般在进料口 以上，塔顶几块板下加 入。溶剂进口以上部分 称为溶剂回收段。 2）若进料是最高恒沸物， 溶剂与加料一块加入。
加入位置还与萃取剂的 性质有关。
2021年6月
26
二、萃取原理-溶剂的作用
-增大原有组分的相对挥发度
A2s
如果 xs =0
ln(
1 2
)
s
A21 1 2x1
或
ln = ln(
p
s 1
ps2
)T2
A21 1 2x1
忽略温度对蒸汽压比值的影响，在x1 x1时，可得出：

多组分精馏专

多组分精馏专

3.3 最少理论板数 Nmin
精馏塔在操作过程中，将塔顶蒸气全部冷凝， 精馏塔在操作过程中，将塔顶蒸气全部冷凝，其 凝液全部返回塔顶作为回流，称此操作为全回流， 凝液全部返回塔顶作为回流，称此操作为全回流，回 流比R为无穷大（R=∞）。 此时通常不进料，塔顶、 流比R 为无穷大（ R=∞） 此时通常不进料， 塔顶 、 塔底不采出。故精馏塔内气、液两相流量相等， 塔底不采出 。 故精馏塔内气 、 液两相流量相等 ， L = 两操作线效率均为1 并与对角线重合。 V，两操作线效率均为1，并与对角线重合。由于全回 流操作时，使每块理论板分离能力达到最大， 流操作时，使每块理论板分离能力达到最大，完成相 同的分离要求，所需理论板数最少， 同的分离要求，所需理论板数最少，并称其为最小理 论板数Nmin 。
即
ϕ l＝DxD,l/Fzl
某精馏塔进料中含n-C600.33， n［ 例 ］ ： 某精馏塔进料中含 ， C700.33， n-C800.34。 要求馏出液中 ， 。 要求馏出液中n- C70 含量不大于0.011，釜液中 含量不大于 ，釜液中n-C60含量不大于 0.015(以上均为摩尔分数 。 若进料流率为 以上均为摩尔分数)。 以上均为摩尔分数 100kmol／h，试求馏出液和釜液的流量及 ／ ， 组成。 组成。
W,x W,i ,w i
总物料衡算式： 总物料衡算式： F=D+W 组分物料衡算式： 组分物料衡算式： fi=di+wi 对于轻组分i w =0； 对于轻组分i： i=0；di=fi 对于重组分j：j=0；wj=fj 对于重组分j d =0； 馏出液的流量 D=∑di+dl+dh=∑fi+dl+dh 塔釜液流量 W=∑wj+wl+wh=∑fj+wl+wh 1≤i≤l－ 1≤i≤l－1 h+1≤j≤c

第三章多组分精馏

第三章多组分精馏

第三章多组分精馏⼀、填空题1、仅在塔顶或塔釜出现的组分为（）。

2、在多组分精馏过程中，全回流时所需理论板数（），在最⼩回流⽐下所需理论板数（）。

3、萃取精馏塔在萃取剂加⼊⼝以上需设（）。

4、恒沸精馏过程恒沸剂的加⼊不仅影响原溶液组分( )，同时与原溶液中的⼀个或⼏个组分形成恒沸物，当形成最低温度的恒沸物时恒沸剂从塔（）出来。

5、关键组分中，挥发度⼤的组分为（）；挥发度⼩的组分为（）。

6、清晰分隔法的假设为（），（）。

7、在多组分精馏过程中，由芬斯克公式计算的最少理论板数决定于两组分的分离要求和（），与进料组成（）。

8、萃取精馏是指原溶液加⼊新组分后不形成共沸物且S 沸点（），从（）采出。

9、多组分精馏中，关键组分是指（）的组分。

10、常⽤吸附剂有（），（），（），（）。

⼆、单项选择题1、多组分精馏中，若轻重组分均为⾮分配组分，则恒浓区出现在：( )(A) 精馏段和提馏段中部 (B) 精馏段中部和板下紧靠进料板处(C) 板上仅紧进料板处和提馏段中部 (D) 板上、下紧靠进料板处2、对⼆元均相共沸物，s i P 相差增⼤，最低共沸物向哪个区移动：( )(A) ⾼沸点组分多浓度区 (B) 低沸点组分多浓度区(C) ⾼沸点组分低浓度区 (D) 低沸点组分低浓度区3、在均相恒沸物条件下，活度系数和压⼒关系为：( ) (A) 1221γγ=s s p p (B) 2121γγ=s s p p (C) 1221γγ≥s s p p (D) 2 121γγ≤s s p p4、多组分精馏中，若轻重组分均为分配组分，则恒浓区出现在:( )(A) 精馏段和提馏段中部 (B) 精馏段中部和板下紧靠进料板处(C) 板上仅紧进料板处和提馏段中部 (D) 板上、下紧靠进料板处5、萃取精馏塔内⽓液相流率的分布规律为:( )(A) 从上到下⽓液相流率逐渐增⼤，液相流率远⼤于⽓相流率(B) 从上到下⽓液相流率逐渐减⼩，液相流率远⼤于⽓相流率(C) 从上到下液相流率增⼤，⽓相流率减⼩，液相流率⼩于⽓相流率(D) 不确定6、下列不属于以压⼒差为推动⼒的膜分离技术为:( )(A) 微滤 (B) 超滤 (C) 反渗透 (D) 渗析7、液相进料的萃取精馏过程，应该从何处加萃取剂：( )(A) 精馏段 (B) 提馏段 (C) 精馏段和进料处 (D) 提馏段和进料板8、当萃取塔塔顶产品不合格时，可采⽤下列⽅法来调节：( )(A) 加⼤回流⽐ (B) 加⼤萃取剂⽤量(C) 增加进料量 (D) 减⼩萃取剂⽤量9. 吉利兰关联图，关联了四个物理量之间的关系，下列哪个不是其中之⼀:( )(A) 最少理论板书 (B) 最⼩回流⽐(C) 压⼒ (D) 理论板书三、简答题1、试分析多组分精馏在最⼩回流情况下，恒浓区出现的位置。

第三章 精 馏(分离工程,叶庆国)

第三章 精 馏(分离工程,叶庆国)
第三章 精 馏
3.1 多组分精馏
3.1.1 多组分精馏过程分析
3.1.2 多组分精馏的简捷（群法）计算法
精馏：distillation
精馏是多组分分离中最常见的单元操作，它
是利用组分挥发度差异，借助“回流”技术 实现混合液高纯度分离的多级分离操作，即 同时进行多次部分气化和部分冷凝的过程。 实现精馏操作的主体设备是精馏塔。
Nm
L K , D H K ,W lg (1 L K , D )(1 H K , w )
lg L K H K
Fenske公式计算Nm注意事项
• Fenske公式适用于双组份精馏，也适用于多 组分精馏（可以用一对关键组分来求，也可 用任意两组份来求）。 Nm与进料状态、组成的表示方式无关
i ,n i ,n i ,n
Fenske公式计算Nm
对于任意组分
塔顶为全凝器：x i , D 第一个平衡级 平衡关系：y i ,1 K i ,1 x i ,1 操作关系：x i ,1 y i , 2 联立两式：y i ,1
K i ,1 y i , 2
y i ,l
精馏塔的任务：
LK尽量多的进入塔顶馏出 液； HK尽量多的进入塔釜釜液。
关键组分的指定原则

由工艺要求决定
例：ABCD（按挥发度依次减少排列）混合物分离 ◆工艺要求按AB与CD分开： 则：B为LK；C为HK ◆工艺要求先分出A： 则：A为LK；B为HK
分配与非分配组分
根据组分是否在精馏塔的两端都出现，可分为分配 组分(distributing component)和非分配组分 (nondistribution component)。 分配组分：塔顶、塔底同时出现 非分配组分：只在塔顶活塔底出现的组分

第三章_多组分精馏

第三章_多组分精馏

化工分离工程
第三章 多组分精馏和特殊精馏
设计变量数分为： Nie = NXe － Nae
固定设计变量数NXe 进料物流变量数＋系统压力； 可调设计变量数Nae 除NXe 的其他变量数。
往往对此感兴趣！
例1中分配器： N e = 1 C + 2） 1 = C + 3 （ + x e e N a = N i - N e = C + 4） C + 3） 1 （ = x （
传热单元数目
合计
2
7
化工分离工程
第三章 多组分精馏和特殊精馏
化工分离工程
第三章 多组分精馏和特殊精馏
化工分离工程
第三章 多组分精馏和特殊精馏
3.1 多组分精馏过程
3.2.1 多组分精馏过程分析
3.2.2 最小回流比
3.2.3 最少理论塔板数和组分分配
3.2.4 实际回流比和理论板数 3.2.5 多组分精馏的简捷计算方法
进料 每级压力（包括再沸器）
全凝器压力 回流分配器压力 合计
C+2 N
1 1 C+N+4
回流温度
理论板数
1
1
进料位置
（D/F）
1
1
（LN+1 D）
合计
1
5
化工分离工程
第三章 多组分精馏和特殊精馏
对精馏塔归纳出简便、可靠的确定设计变量的方法： （1）按每一单相物流有（C+2）个变量，计算由 进料物流所确定的固定设计变量数。 （2）确定装置中具有不同压力的数目。 （3）上述两项之和即为装置的固定设计变量数。
注意：同一组分，规定了 一端的回收率，另一端的 量已确定。不能重复！

第三章-多组分精馏

第三章-多组分精馏
31
3.2.4 实际回流比和理论板数
用Underwood方程求出Rm 后，实际回流比R一般 取作1.30Rm。
有了实际回流比和最少理论板数，求实际理论板数 常用的经验方法有：
Gilliland图、Erbar-Maddox图。
适用于相对挥发度 变化不大的情况
适用于非理想性 较大的情况
32
图3-9 Gilliland图
35
3.2.5 多组分精馏的简捷计算方法 精馏简捷计算 ——FUG法
Fenske
Underwood Gilliland
Nm
Rm
R、N
36
开始
指定进料条件
指定两个关键组分的分离程度
估计非关键组分的分离情况
决定精馏塔操作压力和冷凝器类型 （泡、露点计算）
在塔压下作闪蒸计算
（绝热闪蒸计算）
计算最少理论板数和非关键组分的分离程度
多组分精馏 物系组成
轻非关键组分（LNK），轻组分 轻关键组分（LK） 中间组分
重关键组分（HK） 重非关键组分（HNK），重组分
非分配组分：只在塔顶或塔釜出现的组分； 分配组分：在塔顶和塔釜均出现的组分。 11
3.2.2 最小回流比（Rm）
二组分精馏： 最小回流比下，进料板上下出现恒浓区或夹点。
28
讨论与分析：
清晰分割假定比较适用的情况： 轻重关键组分的分离程度较高，轻组分的挥发度比 LK的挥发度大得多，而重组分的挥发度比HK的挥 发度小得多。
对于无中间组分的体系： 如A(LNK)、B(LK)、C(HK)、D(HNK)组成的体系， 先假定清晰分割，计算理论板数，再校验是否清晰 分割。
对于有中间组分的体系： 如A(LNK)、B(LK)、C(中间组分)、D(HK)、 E(HNK) 组成的体系，则根据C的相对挥发度是靠近 B还是靠近D来假定C在塔顶和塔釜的分配。

3.1 多组分精馏过程


轻组分恒浓区
24
3.1.2 最小回流比（Rm）
（2）重组分为非分配组分，轻组分为分配组分：
（3）重组分为分配组分，轻组分为非分配组分：
25
3.1.2 最小回流比（Rm）
（4）轻、重组分均为分配组分：
最小回流比条件下会出 现恒浓区，区内无分离 效果，需无穷多理论板。 如何计算最小回流比？
26
3.1.2 最小回流比（Rm）
3.1.2 最小回流比（Rm）
为完成某一分离任务，所需的理论塔板数为无穷多
时的回流比称为最小回流比。
二组分精馏：
最小回流比下，进料板上下出现恒浓区或称夹点。
恒浓区
多组分精馏：
最小回流比下，也有恒浓区，但由于非关键组分
的存在，恒浓区出现的部位要较二组分精馏复杂。
23
3.1.2 最小回流比（Rm）
一、关键组分（Key Components）
串级数(2) 分配器(1) 侧线采出(0) 传热单元(2)
Na=5
F
已被指定的可调变量：
余下的2个可调
（1）进料位置；（2）回流比；
（3）全凝器饱和液体回流或冷凝器 的传热面积或馏出液温度。
设计变量往往用来 指定组分在馏出液 和釜液中的浓度。
4
3.1.1 多组分精馏过程分析
第三章 多组分精馏和特殊精馏

3.1 多组分精馏过程 ★ 3.2 萃取精馏和共沸精馏 ★ 3.3 反应精馏
3.4 加盐精馏
重点-多组分多级分离过程分析和简捷计算!
3.1 多组分精馏过程

3.1 多组分精馏过程

3.1.1 多组分精馏过程分析

1 、关键组分 2、 组分在塔顶、塔底产品中的预分配 3 、多组分精馏过程特征

化工分离工程第3章 多组分精馏2


FLGC
3.3.6 共沸与萃取精馏比较
共同点: 加入溶剂S， 萃取精馏的优点：
12 / s
(1) 因萃取精馏溶剂沸点高，溶剂可从塔顶或附近加入，使
全塔的相对挥发度都得到提高。
(2) 萃取精馏溶剂在塔内基本上不挥发，能量消耗少。而共
沸精馏中共沸剂与原料组分同时气化，消耗能量。
(3) 共沸精馏由于必须形成共沸物，因而可供选择的共沸剂
FLGC
特殊精馏
• 普通精馏不适合于以下状况的物料： 1、相对挥发度接近1的组分； 2、待分离组分间形成共沸物； 3、待分离组分是热敏物质； 4、待分离组分是难挥发组分，且含量低。
特殊精馏——利用加入热能和质量分离剂以增加原有组 分间的相对挥发度值的精馏方法。
FLGC
常用的特殊精馏方法
• 共沸精馏——如果加入的第三组分能和被分离物系中一个 或几个组分形成共沸物时，第三组分以共沸物的形式从精 馏塔塔顶蒸出。所加入的新组分称为共沸剂。
方案2：选择丙酮的同系物，则塔顶产物为甲醇，塔釜为丙酮及同
系物
哪个更好？
FLGC
（2）从分子结构相似（或极性相似）的概念选择溶剂 常见有机化合物按极性增加的顺序排列为： 烃→醚→醛→酮→醇→二醇→水 应选择在极性上更类似于重关键组分的化合物为溶剂， 可以有效的减小重关键组分的挥发度！
同样如甲醇（沸点64.7）—丙酮（沸点56.5）体系 选烃为溶剂，烃与丙酮极性相似，塔顶产物为甲醇，塔
FLGC
萃取精馏的注意事项：
（1）由于加入的萃取剂是大量的（一般要求xs>0.6）,因此塔内下 降液量远大于上升蒸汽量，造成汽液接触不佳，故萃取精馏塔 的塔板效率低，大约为普通精馏的一半左右(回收段不包括在 内)。设计时要考虑塔板及流体动力情况。

多组分精馏简述

第三章 多组分精馏在化工原理课程中，对双组分精馏和单组分吸收等简单传质过程进行过较详尽的讨论。

然而，在化工生产实际中，遇到更多的是含有较多组分或复杂物系的分离与提纯问题。

在设计多组分多级分离问题时，必须用联立或迭代法严格地解数目较多的方程，这就是说必须规定足够多的设计变量，使得未知变量的数目正好等于独立方程数，因此在各种设计的分离过程中，首先就涉及过程条件或独立变量的规定问题。

多组分多级分离问题，由于组分数增多而增加了过程的复杂性。

解这类问题，严格的该用精确的计算机算法，但简捷计算常用于过程设计的初始阶段，是对操作进行粗略分析的常用算法。

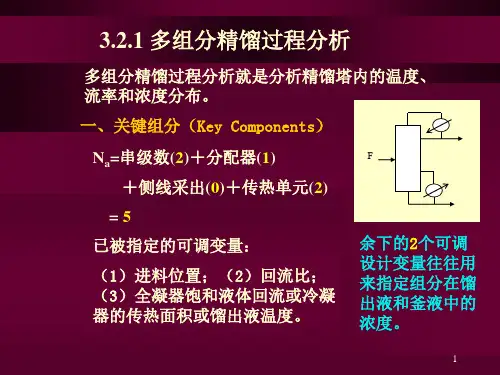
§3-1分离系统的变量分析设计分离装置就是要求确定各个物理量的数值，但设计的第一步还不是选择变量的具体数值，而是要知道在设计时所需要指定的独立变量的数目，即设计变量。

一、设计变量1.设计变量⎩⎨⎧-=：可调设计变量固定设计变量a x c v i N N N N N :v N ：描述系统所需的独立变量总数。

c N ：各独立变量之间可以列出的方程式数和给定的条件，为约束关系数。

要确定i N ，需正确确定v N 和c N ，一般采用郭慕孙发表在AIchE J （美国化学工程师学会），1956（2）：240-248的方法，该法的特点是简单、方便，不易出错，因而一直沿用至今。

郭氏法的基本原则是将一个装置分解为若干进行简单过程的单元，由每一单元的独立变量数e v N 和约束数e c N 求出每一单元的设计变量数e i N ，然后再由单元的设计变量数计算出装置的设计变量数E i N 。

在设计变量i N 中，又被分为固定设计变量x N 和可调设计变量a N ，x N 是指确定进料物流的那些变量（进料组成和流量）以及系统的压力，这些变量常常是由单元在整个装置中的地位，或装置在整个流程中的地位所决定，也就是说，实际上不要由设计者来指定，而a N 才是真正要由设计者来确定的，因此郭氏法的目的是确定正确的a N 值。

第三章 多组分精馏


层理论塔板才能满足分离要求所需的回流比，
称为最小回流比。多组分精馏计算中，必须用
解析法求最小回流比。
23

常用的是恩德伍德法，推导该式的基本假设是：
1) 体系中各组分的相对挥发度为常数；
2) 塔内气相和液相均为恒摩尔流。

根据物料平衡及相平衡表示，利用恒浓区的 概念，恩德伍德推导出最小回流比的两个联 立公式：

清晰分割时非关键组分在塔顶和塔底产品
中的分配用物料衡算求得。
11
12
总物料衡算 苯的衡算 乙苯的衡算
甲苯的衡算
13
(2) 非清晰分割

如果轻重关键组分不是相邻组分，则塔顶和塔 底产品中必有中间组分。 如果进料液中非关键组分的相对挥发度与关键 组分相差不大，则塔顶产品中就含有比重关键 组分还重组分，塔底产品中含有比轻关键组分
37
应用：实验制备的小批量物质分离、石油产 品评价、高效填料的性能测定、精细化工产
品的提纯、同位素产品的精制等。
计算：难以采用图解方法求解理论板数，通常
采用解析方法或简捷法确定理论板数、进料位
置等。计算中，精密精馏通常按二元混合物处
理。
38
3.5.3
盐溶精馏（加盐精馏）
一种采用特殊萃取剂的萃取精馏，用于难分 离混合物的分离。 例：乙醇-水 、丙醇-水、水-醋酸等的分离
5

对于双组分精馏；
塔顶：xDA 已确定 xDB =1- xDA ;
塔釜：xWB已确定 xWB =1- xWA ;

也就是塔顶、塔釜组成全部确定。

对于多组分精馏：Na=5 ，与组分数无关。
除规定全凝器饱和液体出料：2） R; 3）D/F外只
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、填空题
1、 仅在塔顶或塔釜出现的组分为（ ）。

2、 在多组分精馏过程中，全回流时所需理论板数（ ），在最小回流比下所需理论板数
（ ）。

3、 萃取精馏塔在萃取剂加入口以上需设（ ）。

4、 恒沸精馏过程恒沸剂的加入不仅影响原溶液组分( )，同时与原溶液中的一个或几
个组分形成恒沸物，当形成最低温度的恒沸物时恒沸剂从塔（ ）出来。

5、 关键组分中，挥发度大的组分为（ ）；挥发度小的组分为（ ）。

6、 清晰分隔法的假设为（ ），（ ）。

7、 在多组分精馏过程中，由芬斯克公式计算的最少理论板数决定于两组分的分离要求和
（ ），与进料组成（ ）。

8、 萃取精馏是指原溶液加入新组分后不形成共沸物且S 沸点（ ），从（ ）
采出。

9、 多组分精馏中，关键组分是指（ ）的组分。

10、 常用吸附剂有（ ），（ ），（ ），（ ）。

二、单项选择题
1、 多组分精馏中，若轻重组分均为非分配组分，则恒浓区出现在：( )
(A) 精馏段和提馏段中部 (B) 精馏段中部和板下紧靠进料板处
(C) 板上仅紧进料板处和提馏段中部 (D) 板上、下紧靠进料板处
2、 对二元均相共沸物，s i P 相差增大，最低共沸物向哪个区移动：( )
(A) 高沸点组分多浓度区 (B) 低沸点组分多浓度区
(C) 高沸点组分低浓度区 (D) 低沸点组分低浓度区
3、 在均相恒沸物条件下，活度系数和压力关系为：( ) (A) 1221γγ=s s p p (B) 2121γγ=s s p p (C) 1221γγ≥s s p p (D) 2
121γγ≤s s p p 4、 多组分精馏中，若轻重组分均为分配组分，则恒浓区出现在:( )
(A) 精馏段和提馏段中部 (B) 精馏段中部和板下紧靠进料板处
(C) 板上仅紧进料板处和提馏段中部 (D) 板上、下紧靠进料板处
5、 萃取精馏塔内气液相流率的分布规律为:( )
(A) 从上到下气液相流率逐渐增大，液相流率远大于气相流率
(B) 从上到下气液相流率逐渐减小，液相流率远大于气相流率
(C) 从上到下液相流率增大，气相流率减小，液相流率小于气相流率
(D) 不确定
6、 下列不属于以压力差为推动力的膜分离技术为:( )
(A) 微滤 (B) 超滤 (C) 反渗透 (D) 渗析
7、 液相进料的萃取精馏过程，应该从何处加萃取剂：( )
(A) 精馏段 (B) 提馏段 (C) 精馏段和进料处 (D) 提馏段和进料板
8、 当萃取塔塔顶产品不合格时，可采用下列方法来调节：( )
(A) 加大回流比 (B) 加大萃取剂用量
(C) 增加进料量 (D) 减小萃取剂用量
9. 吉利兰关联图，关联了四个物理量之间的关系，下列哪个不是其中之一:( )
(A) 最少理论板书 (B) 最小回流比
(C) 压力 (D) 理论板书
三、简答题
1、 试分析多组分精馏在最小回流情况下，恒浓区出现的位置。

2、描述萃取精馏的原理及萃取剂的作用。

3、描述恒沸精馏的原理。

在 的溶液中加入一个新组分S ，使它对原溶液中各组分产生不同作用，从而改变原溶液组分之间相对挥发度，使系统变的易于分离。

(4分)。

原溶液加新组分后形成最低共沸物从塔顶采出，为共沸精馏(4分)。

4、叙述萃取剂的选取原则。

5、请指出共沸精馏与萃取精馏的主要异同。

共同点：分离原理相同，即通过加入第三组分，改变原溶液待分离组分间的相对挥发度。

（2分）
区别：1. 萃取剂比共沸剂易选择，限制小。

（1.5分）
2. 萃取剂在精馏过程中基本不汽化，耗能低，共沸精馏的能耗一般比萃取精馏大。

（1.5
分）
3. 共沸精馏的操作温度较低，适于分离热敏性物质。

（1.5分）
4. 萃取精馏不易采用间歇操作，共沸精馏可以。

（1.5分）
四、计算题
试求氨仿（1）—乙醇（2）在共沸温度为55℃时的共沸组成和总压力。

（下式中t 的单位是℃；P 的单位是kPa ）（10分）
已知：
)66.159.0(ln 1221x x +=γ )66.142.1(ln 2212x x -=γ
t P s +-=2270.116302818.6lg 1 t
P s +-=48.23105.165233827.7lg 2 五、计算题（10分）
1,11212≈=α
α
用图中所示系统冷却反应器出来的物料，并从较重烃中分离轻质气体。

计算离开闪蒸罐的蒸汽组成。

从反应器出来的物料温度811K ，Ψ=0.87。

组成如下表。

闪蒸罐操作条件下各组分的K 值：氢-80；甲烷-10；苯-0.01；甲苯-0.004
以氢为1，甲烷为2，苯为3，甲苯为4。

总进料量为F=460kmol/h
4348.01=z （1分）
，4348.02=z （1分），1087.03=z （1分），0217.04=z （1分）
又K 1=80，K 2=10，K 3=0.01，K 4=0.004 Ψ=0.87，
由式
（2分）
计算得：y 1=0.4988 （1分），y 2=0.4924 （1分），y 3=0.008 （1分），y 4=0.0008 （1分） ⎩⎨⎧-+=)1(1i i i i K Z K y ψ。